寻根溯源话试题 拓展探究促提升——2022年武汉中考数学试题第23题的拓展与探究

项 当

(光谷汤逊湖学校，湖北 武汉 430072)

1 考题再现

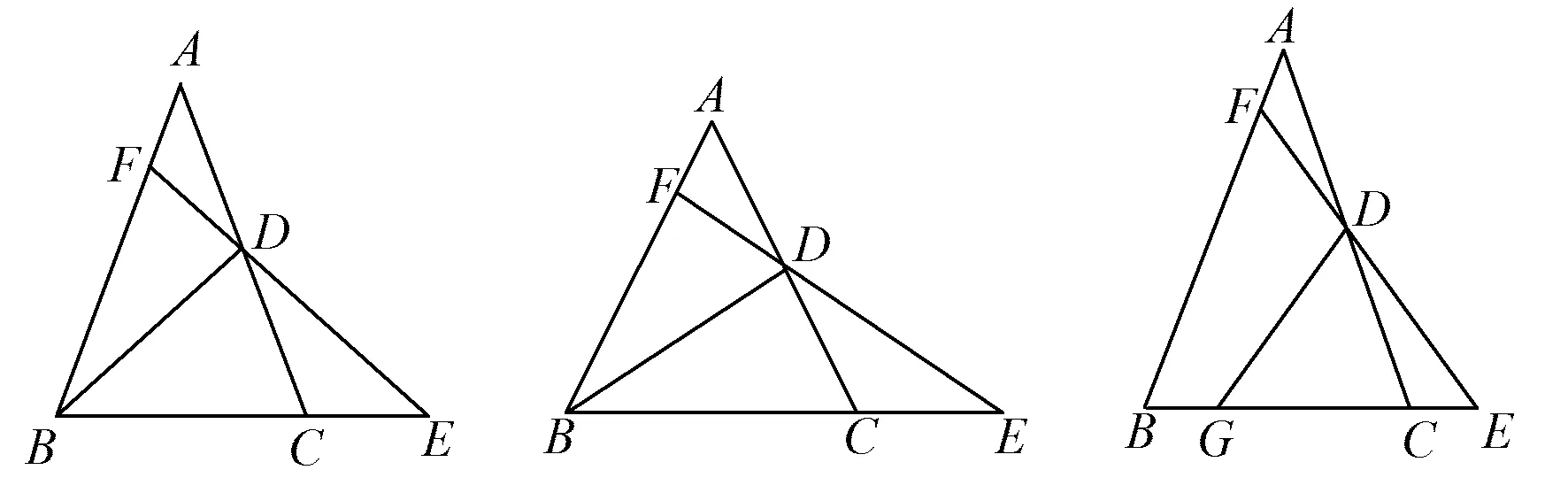
图1 图2 图3

2)再探究一般情形．如图1，证明探究1)中的结论仍然成立.

(2022年湖北省武汉市数学中考试题第23题)

2 课本原型

纵观题干和图形，发现例1以课本习题为背景，在熟悉的基本图形中延长ED，与AB相交于点F，提升了学生识图的难度，从条件特殊到一般，再过渡到特殊，探究结论的相似之处.

例2如图4，△ABC是等边三角形，BD是中线，延长BC至点E，使CE=CD，求证：DB=DE.

图4

(人教版《数学》八年级上册第93页第13题)

3 试题评价

2022年是实施“双减”政策下的首次中考，武汉市在此政策下继续围绕核心素养、依标务本的理念命制试题.例1与往年试题结构、题型、难度上保持一致，但“稳中出变，变中求新，新中求进”，在背景材料选择上更倾向于教材习题，源于课本，却又高于课本，即“题在书外，根在书内”，充分站在学生的立场，聚焦学情，体现了试题的人文和谐，呼唤人本回归；试题图形简洁明了(基本图形为两个底边在一条直线上的等腰三角形，其中一个等腰三角形顶点在另一个等腰三角形的腰上)，文字简练准确，整体呈现和谐流畅.

试题设置不同能力进阶的问题，第1)小题将条件特殊化，通过∠ABD=∠ADF，证明△AFD∽△ADB，可快速解题，并且后面两个小题方法一脉相承.不少学生紧盯等边三角形、含30°直角三角形相关的边与边之间性质，结合分支特殊条件解决第1)小题，但不利于后面小题的解答，属于识图推理题，相对简单.第2)小题将条件弱化，由等边三角形过渡到一般等腰三角形，从特殊到一般，可继续沿用第1)小题的相似方法，抓住不变的特征，灵活运用比例线段的关系进行证明与计算，进而解决第2)小题.不少学生用给出的中点引入辅助线，使得解答过于繁杂.本题综合考查了学生的逻辑推理、直观想象、模型意识等，若方法不当，则会使解答过程较第1)小题困难.第3)小题继续弱化条件，图形变复杂，线段关系进一步隐蔽，方法尽管与第2)小题一脉相承，但需要学生仔细考虑，引入必要的辅助线，在图形的“生长”过程中，体会知识间的纵横、因果、异同等关系，较高程度地考查了学生通过类比迁移从观察到分析、再到解决问题的综合能力，继续落实学科核心素养，题目较综合，难度偏大.总之，学生通过拾级而上、渐次深入的问题解答,实现从低阶思维到高阶思维的提升.让学生学有所答，答有所获，从而增强数学学习的获得感.

4 解法探究

1)解由AB=AC,∠BAC=60°可知△ABC为等边三角形，D是AC的中点，则

由

∠ABC=∠ACB=60°，

得

∠ABD=∠DBC=30°，

又

DB=DE，

故

∠DBE=∠DEB=30°.

因为

∠CDE+∠DEC=∠ACB，

所以

∠ABD=∠CDE=∠ADF=30°，

由

∠ADF=∠ABD=30°， ∠BAD=∠DAF=60°，

得

△AFD∽△ADB，

从而

于是

评注本题巧妙地将两个等腰三角形的底边在一条直线上重合，结合特殊条件60°角，运用等腰三角形和等边三角形的性质进行导角，找到一对相似三角形，确定线段的比例关系.本题起点虽低，但意义颇深，启示深远，埋下了△AFD∽△ADB的恒成立关系，后面的第2)和第3)小题需要学生在图形的变化中抓住这一不变性解题，充分体现了转化思想，考查了学生的运算推理能力.

2)思路1延续第1)小题的方法，直接证△AFD∽△ADB.

证法1由AB=AC,∠ABC=∠ACB，∠ABC=∠ABD+∠DBC，DB=DE，∠DBE=∠DEB，因为

∠CDE+∠DEC=∠ACB=∠ABC，

所以

∠ABD=∠CDE=∠ADF.

又D是AC的中点，从而

由∠ADF=∠ABD，∠BAD=∠DAF，得

△AFD∽△ADB，

从而

于是

思路2利用平行线构造相似.

证法2如图5，取BC的中点H，联结DH.由D是AC的中点，得

图5

DH

又AB=AC，从而

DH=DC，

于是

∠DHC=∠DCH.

因为BD=DE，所以

∠DBH=∠DEC,

从而

∠BDH=∠EDC,

于是

△DBH≌△DEC,

即

BH=EC,

亦即

又因为DH∥AB,所以

△EDH∽△EFB,

从而

于是

故

第1类过点A作平行线，如图6和图7所示.

图6 图7

模型应用图6形成X+X型；图7形成A+A型.

第2类过点C作平行线，如图8和图9所示.

图8 图9

模型应用图8形成A+A型;图9形成X+A型.

第3类过点E作平行线，如图10和图11所示.

图10 图11

模型应用图10形成X+X型;图11形成A+A型.

第4类过点B作平行线，如图12和图13所示.

图12 图13

模型应用图12形成X+A型;图13形成X+A型.

第5类过点D作平行线，如图5和图14所示.

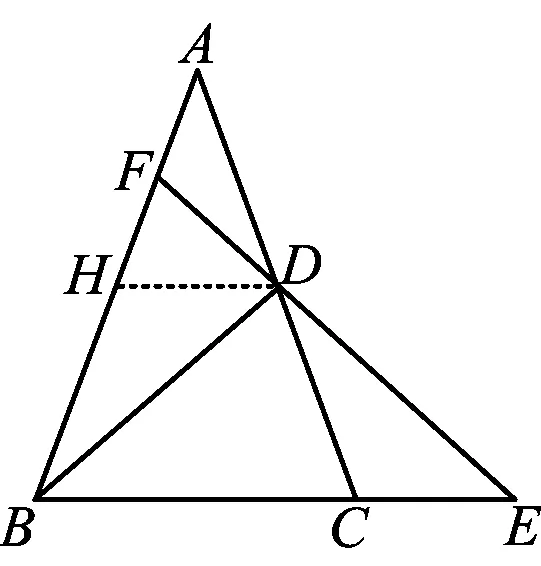
图14

模型应用图14形成X+X型.

评注本题条件虽然一般化，但思路1与第1)小题一脉相承，直接证明可套用第1)小题的解题过程，关键是找出∠BAD=∠DAF不变量，证明△AFD∽△ADB.思路2呈现的是大多数学生引入辅助线的做法，平行线分线段成比例定理，将未知线段比转化为已知线段比，利用出现的重组相似型或者利用平行线分线段成比例找到突破口.

3)解法1(构造A型相似)如图15，取BC的中点H，联结DH，易证

图15 图16

△DGH≌△ECD，

则

GH=CE，

从而

于是

易得

△EDH∽△EFB，

即

又

因此

即

解法2如图16，过点C作CH∥EF交AB于点H，则

∠HCB=∠E=∠DGC， ∠ABC=∠ACB，

易得

△HBC∽△DCG，

即

设CD=2，则

HB=2n，AB=AC=4，AH=4-2n，AF=2-n，

得

解法3如图17，延长AB和DG相交于点H.取BC的中点M，联结DM，由DG=DE，可知

图17

∠BGH=∠DGE=∠DEG.

由AB=AC，∠ABC=∠ACB，∠HBG=∠DCE，得

∠BHG=∠CDE=∠ADF，

又∠DAF=∠HAD，则

△AHD∽△ADB，

从而

设AD=CD=m，则AB=2m.设CG=1，则BC=n.易知

由△DMG∽△HBG，得

即

从而

故

评注本题方法可以类比第2)小题的解答思路，方法还有多种，由于篇幅有限，不一一罗列.第3)小题使得两个等腰三角形的点B(G)不重合，所给条件更加一般化，不变的是两个等腰三角形底边仍然重合在一条直线上，需要学生从隐藏的图形中学会类比迁移来分析并解决问题.遇到求线段比问题时，若苦于无法找到两条线段之比的中间过渡元素，则思维容易陷入困境.一般来说，遇到“六点四线”型使用直接法做不出来之时，可以添加平行线导比转化.此题引导学生理解数学，真正发挥数学学科的核心素养和育人导向功能.

5 结论拓展

追根溯源此背景图，可以发现解题题眼在于有两组恒成立等角关系，即∠ABD=∠CDE，∠BFE=∠BDC，从而引申出全等和相似.笔者发现，当点D不是中点时，结论仍然成立，情况如下：

1)如图18，点D在AC上，不是AC的中点.

图18 图19

2)如图19，点D在AC的延长线上.

3)如图20和图21，点D在CA的延长线上.

图20 图21

总结对于两个等腰三角形的底边在同一条直线上、一个等腰三角形的顶点在另一个等腰三角形的一腰所在直线上时，总有两个等腰各自同一侧腰(左左和右右)构成的夹角相等.另外，两个等腰各自相反侧腰(左右和右左)构成的夹角相等，即“共底双等腰，等角腰中藏”，并且类似于以上,在：①AB=AC, ②DB=DE， ③∠CDE=∠ABD或∠BFE=∠BDC这3个条件中，我们都可以知二求另外一个结论.

6 教学启示

在“双减”下的数学教学中，频繁的刷题训练只会导致作业负担和课堂低效，是摧毁教学质量的最大顽固.鉴于此，在实际教学中，教师应合理使用教材进行教学，用心领会教材蓝本的精髓，挖掘和拓展课本中习题设计的内在教育价值，学会将复杂图形进行“削枝剪叶留主干，追本溯源寻本质”，同时要由浅入深，由繁到简，循序渐进，形成一系列的问题串、方法链、知识网，引导学生做到一题多解探根源，多法归一促思维，提升学生综合运用知识的能力，激发学习兴趣，提升数学思维能力，让教材的使用更加有效，从而使数学课堂学习更加高效.