一则学生离奇错题案例引发的无理数教学的深度思考
王红权, 李 馨
(1.杭州市基础教育研究室,浙江 杭州 310003;2.拱墅区教育研究院,浙江 杭州 310005)
图1是笔者在朋友圈里看到的一则学生错解案例,很离奇也很有趣,更值得数学教师反思.

图1
图1显示的是学生的错解,在错解边上的空白处,教师有两句评语:“单位长度呢?数轴乱了!”对此,征集了150余位教师的反馈,观点整理如下:
师1:数轴必须等距标注位置,否则就失去了数轴的价值.

师3:数轴的“三要素”是对的,问题出在无理数大小的直观还没有建立.
师4:学生混淆了“单位”“等距”和“有序”这些概念.
师5:归根结底是没有真正理解无理数.
师6:学生的解答很有创意,要在数轴上表示无理数,如果单位长度也是无理数,那么二者统一又方便.
师7:强人所难,这是学生的无奈之举.
师8:学生做这个习题不适合,说明作业设计任重道远.
1 归因分析
1.1 学生认知结构与认知水平分析
学生已经学习了有理数、有理数运算和实数的基础知识(按照浙教版的内容顺序判断),数轴在有理数性质这章学习.从答题情况可以看出:1)数轴“三要素”已基本掌握;2)一类带根号的无理数的大小已基本掌握;3)“每个实数在数轴上都有唯一确定的一个点与之对应”也清楚.
这些内容都是数轴基础知识学习的正迁移,说明初始学习数轴知识基本达标.在学习一种新数(无理数)后出现错误,这表明问题出在新数的学习上.
1.2 “认识无理数”教学分析
1)从无理数“概念”入手的学习.无理数是无限不循环小数.这是无理数的表示而并非定义,其中的关键词“无限”“不循环”无法用数学符号刻画.因此,这样的“概念”不足以判定一个数是否是无理数.
存在:信其有,即要让学生相信一个面积为2的正方形是存在的,因此这个正方形的边长是确定的,但又找不到一个有理数可以用来表示这个边长.
运算:本质上属于极限运算,但也遵循四则运算的基本规律.
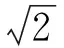
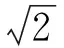
(n+1)-n=n-(n-1),

4)数轴上存在一个点表示无理数和用尺规作图找到这个点是两码事.数轴上的点和实数一一对应,也就是说在数轴上表示某个无理数的对应点是唯一存在的,位置也是确定的.至于能否用尺规作图的方法找到这个点,属于是否可以用尺规作图的问题,并不是同一个问题.
1.3 教师评语分析
教师有两句评语:单位长度呢?数轴乱了!

学生会觉得“数轴乱了”吗?如此思维有“创意”、视觉“有序”、极具“美感”的数轴,哪里乱了?对于这样的认知冲突教师该如何处理,这非常考验教师的功力(教师本体知识的理解水平、教材处理能力和教学组织管理能力)!
2 重新设计“实数”教学片段
2.1 借助直观,信其有得其法
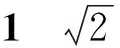

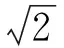


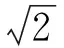
2.2 通过证明,悟其理品其性


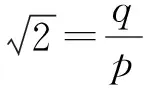
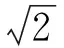
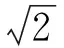
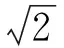
设计意图通过对无理数和实数下定义和分类,结合前面的学习,学生感知到无理数有正负的性质,能和有理数比较大小,这样有理数和无理数就可以在一个体系(实数)中加以研究.为接下来研究无理数的性质(大小关系、运算)奠定基础.
2.3 通过辨析,解其疑知其美
例1判断下列说法是否正确:

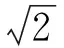
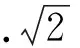

例3面积为2与面积为3的正方形的边长哪个较大?
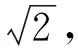

图2



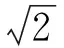


图3
设计意图通过示范与动手,学生明确数轴上的点与实数一一对应,感受数学之美(形与数的完美结合).进一步确定数轴上存在一个点表示某个实数,和在数轴上用尺规作图找到这个点的具体位置是两件不同的事.
2.4 通过小结,使之精使之简
学习路径如图4.

图4
2)类比有理数的学习过程,我们又是如何学习实数的?
按照:“概念(定义、分类、表示)—性质(大小关系)”的一般套路进行(如图5).

图5
设计意图通过知识框图,回顾研究一个“新数”的一般方法,建构新旧知识之间的联系,挖掘内容所蕴涵的数学思想方法,组织形成有序的内容结构,凝练本单元的教学主题.
3 后记
无理数的大小可以借助有理数进行估计,引题中学生的离奇错误反映出学生对无理数的性质(大小关系)理解偏差,问题的根源在于教学设计,只有纳入教学设计的作业设计才能发挥作业应有的价值.理解数学是一切教学设计之源,教师当任重而道远.

