欲“得其中” 须“取法乎上”
——一道基于尺规作图的综合与实践试题的命题启示
石树伟
(广陵区教师发展中心,江苏 扬州 225006)
古人云:“取法乎上,仅得其中;取法乎中,仅得其下.”意思是做一件事情,高标准的要求只能得到中等的结果,中等标准的要求只能得到下等的结果.反过来,欲“得其中”,须“取法乎上”.笔者从一道基于尺规作图的综合与实践试题的命题过程得到启示:要命制一道好的试题,须坚持高标准要求.
1 试题的命题过程
在2022年的中考命题中,笔者所在命题组领衔命制了一道基于尺规作图的综合与实践试题,感触颇深.现将此题的命题过程撷取重要环节和关键变化回顾如下.
1.1 命题初思及试题初稿
《义务教育数学课程标准(2022年版)》(以下简称《新课标》)已经正式发布,其中一个重要变化就是凝练、明晰了义务教育阶段的数学学科核心素养——“三会”,几何直观、推理能力是初中阶段“三会”的两个主要表现.为落实上述核心素养和具体表现,《新课标》在教学内容上也做了相应调整,特别是对尺规作图提出了更高要求.为此,笔者拟命制一道尺规作图题,考查学生的基本作图掌握情况,并以此为载体考查学生的几何直观和分析推理能力.根据上述设想,命题组拟定试题初稿如下:
试题初稿用圆规和无刻度的直尺作图:
1)如图1,已知△ABC,请在边BC上作一点D,使S△ABD=S△ACD;
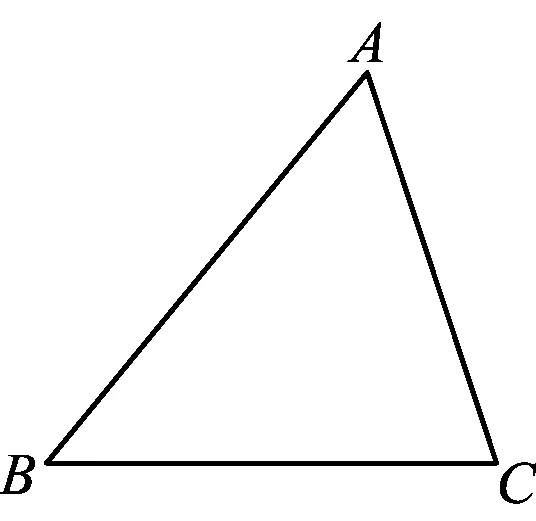
图1
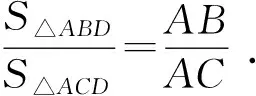
1.2 命题再思及试题二稿

细思试题初稿,笔者发现两个小题之间“形似而神散”,空有外在的“形似”,但任务之间没有内在的联系,“各做各事”,整道题缺少一条主线或一个灵魂.命题组通过集思广益,讨论确定创设一个主题式活动情境,让几个小题聚焦同一个主题或目标——等分三角形面积,分别运用不同思路去完成同一个任务,从而让试题有主线、有灵魂[1].
根据上述设想,命题组拟定试题二稿如下:
试题二稿等分三角形面积.
问题提出如何用圆规和无刻度的直尺作一条直线平分已知三角形的面积?
问题初解如图1,已知△ABC,请用圆规和无刻度的直尺过点A作一条直线,使△ABC的面积被这条直线平分.
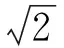

图2
问题再解如图1,已知△ABC,请用圆规和无刻度的直尺作一条与边BC平行的直线,使△ABC的面积被这条直线平分.
1.3 命题三思及试题终稿
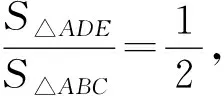
即
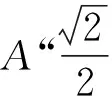
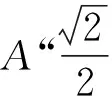

试题终稿等分扇形面积.
问题提出如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?
问题初解如图3,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分.

图3
问题联想如图2,已知线段MN,请你用圆规和无刻度的直尺作一个以MN为斜边的等腰Rt△MNP.
问题再解如图3,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧,使扇形的面积被这条圆弧平分.
1.4 试题终稿反思及评析


图4
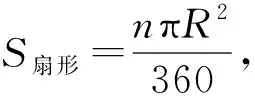
2 命题启示
该试题的命制过程给笔者最大的启示就是命题工作要坚持高标准要求,“取法乎上”才能“得其中”.
1)启示之一:欲“得其中”,须“取法乎上”.
欲“得其中”,须“取法乎上”,即要命得满意的试题,就必须坚持高标准要求.在命题及打磨过程中,要重视每位成员的每一个疑问、每一个不满意不舒服的感觉,每一个疑问、每一个不满意不舒服的感觉就是试题优化或升华的源泉.咬定目标不畏难、不妥协,要相信办法总比困难多,凝聚集体智慧,集思广益,不达目的誓不罢休.
人们常说好事多磨,命题是“好题多磨”.这绝不是大道理,也绝不是空话、套话,而是笔者在命题过程中的切身体会.在该试题的命制过程中,从“等分三角形面积”到“等分扇形面积”,研究主题升华的这个过程非常艰辛,冥思苦想而不得,中途也有“学生能做就行,再改太难了,改不出来了,就这样过去吧”的声音,甚至有放弃此题的想法.但笔者所在命题组都坚持下来了,在解决试题二稿“问题再解”中作图痕迹(弧线)过多的问题时,一箭双雕获得了一个全新主题,这再次印证了“好题”需要“多磨”.
2)启示之二:高标准高在试题立意和命题技术要求.命题坚持高标准要求,高标准首先高在试题立意.试题立意要符合新课标、新评价理念,落实立德树人根本任务.在该试题的命制过程中,从试题初稿的“形似而神散”,到试题二稿、终稿以简化的主题式综合与实践活动为载体,在任务完成过程中考查学生的高阶思维能力及数学核心素养发展状况,这个改变与《新课标》关于综合与实践领域的新要求及当前新课程、新评价理念相吻合,体现了正确的教学导向作用.
命题坚持高标准要求,高标准其次高在命题技术要求.命题技术要求很多,除试题的语言表述应力求简明、无歧义外,还常常关注以下3个方面:①试题背景素材的公平性.如该试题的二稿以“等分三角形面积”为研究主题,部分学生可能很熟悉,试题素材有欠公平.②试题的信度.如该试题二稿的“问题再解”中,作图痕迹(弧线)过多且密集,不利于教师阅卷和准确判分,可能会影响试题的信度.③试题的效度.如该试题二稿中的“问题联想”对“问题再解”提示、铺垫过多,思维梯度的设计不够合理,对学生知识迁移应用能力的考查就有所弱化,考查目标难以达成,影响了试题的效度.
本试题在命制过程中,坚持高标准要求,精益求精不放过任何一个不满意之处,最终的试题终稿完美地解决了上述3个方面的不足.
———《扇形的认识》教学廖

