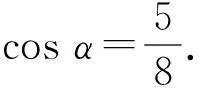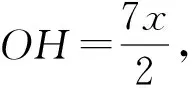聚焦主干突能力 突出素养显内涵
——2022年宁波数学中考试题分析
蔡卫兵, 杨一丽
(1.鄞州实验中学,浙江 宁波 315100;2.宁波市教育局教研室,浙江 宁波 315100)
随着《义务教育数学课程标准(2022年版)》(以下简称《课标》)的颁布,我国数学教育已全面开启了以核心素养为导向的数学课程改革.核心素养指导数学教育改革,尤其是数学考试和评价的改革,我国正式迈进素养导向的数学核心素养评价时代.从应试能力考查过渡到高阶思维认知能力考查,致力于学生的核心素养培育,着眼于人的全面发展.2022年浙江省宁波市数学中考试题坚持“立德树人,引导教学,服务学生发展”的绿色命题理念,着力于数学知识和思想、数学应用和文化,以真实自然的试题材料、突出数学本质的试题内容、新颖的试题呈现方式考查学生的数学学科素养[1].试题布局设计科学合理,遵循课标,稳中有变,扩大选材范围,综合考查“四基”“四能”;聚焦关键能力,重点考查“核心概念和思想方法”;突出素养内涵,有效考查“数学学习过程与潜能”;接轨PISA理念,适度考查颇具“宁波特色”的试题.
1 “五育”并举,促进全面发展
立足立德树人根本任务,贯彻“五育并举”教育方针.从立意和选材上引领学生关注社会现实、时代发展,引导学生徜徉体育运动和艺术经典,助力体美劳教育,强化、凸显数学中考的思想教育和价值引领,用立德树人熔铸数学价值.
第3题以医保信息化、标准化取得里程碑突破为背景,考查科学记数法,进一步发展学生的数感,彰显改革开放以来的建设成就,增强学生的民族自信心和自豪感.
第5题以疫情防控体温监测为背景,考查统计量,进一步培养学生的数据分析观念,融入新冠肺炎疫情,体现社会责任、科学防治、精准施策,共同守护生命安全和身体健康.
第8题利用我国古代数学名著《九章算术》中的“粟米之法”,考查学生用二元一次方程组解决实际问题的能力,体现古代劳动人民的智慧和成果,依托史料,彰显人文价值,激发爱国情怀.
第14题利用国家级的非物质文化遗产中的抖空竹作为背景,考查切线的性质、四边形内角和定理和弧长的有关计算的知识,继承和发扬中华优秀传统文化,体会我国传统文化的博大精深,增强数学应用意识.
第20题以选手参加跑步集训为素材,考查学生观察数据、分析数据及应用数据分析解决问题的能力,引导学生热爱体育,倡导强健体魄,锤炼意志.
第21题应用消防车云梯并结合PISA理念编拟而成,考查三角函数与解直角三角形,加强消防安全知识宣传,提高全民消防安全意识,以科技化手段提升防灭火和应急救援能力,为建设平安和谐社会发挥积极作用,培养学生对社会的责任感、使命感.
第22题以农科院专家指导学生种植小番茄为背景,实现对一次函数、二次函数的考查,使学生认识到劳动创造美好生活的意义,懂得了劳动光荣、劳动致富,弘扬劳动精神,热爱劳动,为人生发展奠定坚实的基础.
2 淡化技巧,注重通性通法
关注四基要求,体现数学基础,注重本原性方法,淡化特殊技巧,强调最合理的想法、最基本的思路、最常用的方式和最普遍的操作程序,注重通性通法的深入理解和综合运用,促进学生将知识和方法内化为自身的知识结构,力图引导中学遵循教学规律、提高课堂教学效果,服务“双减”政策实施,助力基础教育提质增效.
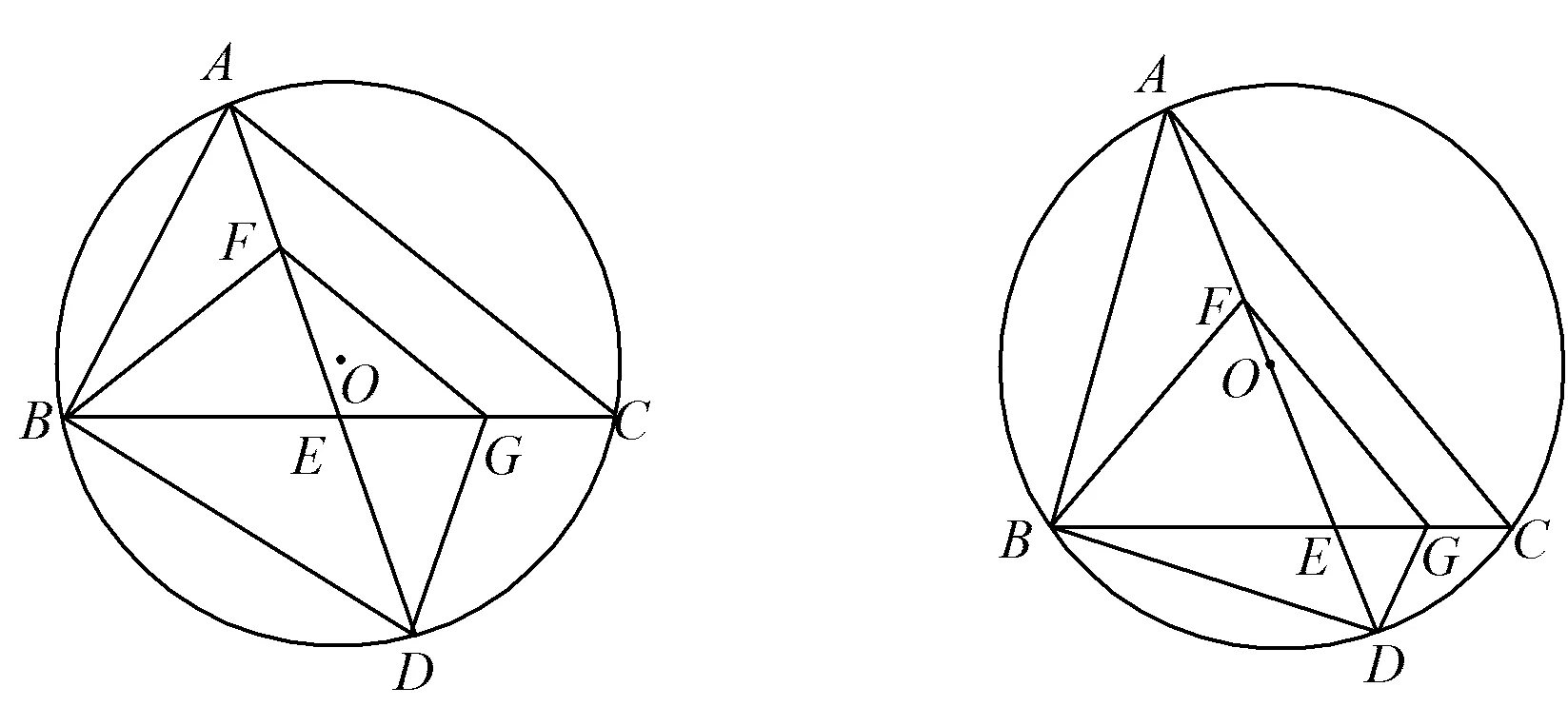
例1点A(m-1,y1),B(m,y2)都在二次函数y=(x-1)2+n的图像上.若y1 ( ) (2022年浙江省宁波市数学中考试题第9题) 分析本题主要考查二次函数的解析式、图像和性质以及学生的画图能力和识图能力.运用数形结合的数学思想方法进行分析,将直观函数图像的概念代入求值,得 y1=(m-2)2+n,y2=(m-1)2+n, 从而 (m-2)2+n<(m-1)2+n, 解得 将直观函数图像的规律进行转化,即点A到对称轴的距离比点B到对称轴的距离近,于是 |m-1-1|<|m-1|, 可根据绝对值的几何意义求得结果.将直观二次函数的性质进行分类:当m-1≥1时,显然成立;当1 故 当m≤1时,显然不成立. 通过直观选项意义进行排除:观察A,B,D这3个选项发现m=2是一个特殊值,此时A(1,y1),B(2,y2),显然满足题意,即可排除选项A,C,D. 例2将两张全等的矩形和另两张全等的正方形纸片按如图1所示的方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出( ) 图1 图2 图3 A.正方形纸片的面积 B.四边形EFGH的面积 C.△BEF的面积 D.△AEH的面积 (2022年浙江省宁波市数学中考试题第10题) 分析本题以矩形纸片为素材,以生成的图形面积为问题核心,将整式的运用、矩形的性质、图形的平移问题融汇在基本图形中,为运用割补、重组、转移、等积变形、以数解形等方式提供平台. 直观数量与数量关系:设正方形纸片的边长为a,矩形纸片的长为b,宽为c,则 2a=b+c, 从而 EH=b-a,EF=a-c=b-a, 于是S阴影=(b-a)2+(b-a)c+(b-a)a=2a(b-a), 故 S阴影=4S△BEF. 直观图形与图形关系:如图2,联结EN,GM,EG,通过线段平移可得EF=EH,从而 S△AEH=S△NEH,S△CFG=S△MFG, S△BEF=S△DGH=S△MEG=S△NEG, 于是 S阴影=4S△BEF. (或如图3,延长HG交BC于点M,延长GF交AB于点P,根据等积变形可得S矩形EFPQ=S矩形EHMN进行求解.)在问题解决的过程中考查学生对于代数式的变形能力以及图形的变换. 主干知识是数学学科理论的基本内容,是考查学生能力与素养的有效途径和载体,更是学生今后生活和学习的基础.关键能力是基于必备知识的提升,是发展学科核心素养的基础.“活”的知识才是能力,“活”的能力才是素养,应注重考查知识的形成过程以及知识之间的内在联系,在知识的应用中不断地深化. 图4 (2022年浙江省宁波市数学中考试题第16题) 分析本题以矩形和对称点为素材、以反比例函数为载体设置问题,实现双曲线与平行线的图形的完美组合,注重核心知识组合与串联,使试题具有综合性和灵活性,达到了用一道题考查诸多核心知识的目的.本题综合考查了初中阶段“数与代数”“图形与几何”的重点知识,矩形性质生长在几何图形变换的应用中,反比例函数的概念生长在面积转换中,平行应用到等积变形中,线段比应用到代数推理中,点的坐标应用到几何性质中,准确把握了几何与函数学习的核心内容和要求,引导学生整体感知图形特征,有利于学生形成数学学习的整体意识. 数学教学的重要目标之一是让学生亲身经历数学知识形成、发展和应用的过程,积累数学活动经验,理解知识本质,感悟数学思想[2].以数学知识、数学规律、数学方法为载体实施即时学习,并运用所得的知识方法探索、研究、解决相关问题,考查核心概念的同时,考查学生对数学思想的感悟与认知,以此来检测学生将知识迁移到不同情境中去的能力,从而检测出学生个体理性思维的广度和深度以及进一步学习的潜能.关注过程方法,活学结合活用,凸显思维发展. 例41)(基础巩固)如图5,在△ABC中,D,E,F分别为AB,AC,BC上的点,DE∥BC,BF=CF,AF交DE于点G,求证:DG=EG. 图5 图6 图7 (2022年浙江省宁波市数学中考试题第23题) 本题呈现形式新颖简约,问题设计坡度合理,连贯有层次,蕴涵丰富的思维,且兼顾整体性,又对“个性发展”的差异性做出有效甄别.以平行相似基本图形中的比例线段为起点,寻找中间比实现等比替换,巧用线段成比例证明线段相等,以此获得线段中点的基本结论,结合垂直进而出现等腰三角形三线合一的基本图形,逆用线段垂直平分线的逆定理实现等量替换线段.在此基础上利用平行四边形对角线的性质隐藏线段中点的条件,去除等腰三角形三线合一的一半图形,根据问题情境的变化,通过类比和引申合理进行思想方法、思维方式和思维策略的迁移,进而转化为背靠背解三角形的基本图形,实现问题的自然转化.体现出试题结构的整体性和系统性,梯度进阶,互相关联,渐次展开,从证明体验(基础巩固)—思考探究(尝试应用)—拓展延伸的学习过程的考查,要求学生学习能够从“知识的回顾”到“本质的理解”再抵达“灵活应用”的层次,为后续的学习积累重要的方法,充分体现建立联系、融会贯通等数学学习过程的意义. 对数学学科来说,特别重要的是淡化记忆,凸显思维.数学思维是学生数学素养的重要体现,试题内容应从核心素养角度出发思考需要的数学知识与能力,将数学知识与核心素养有机融合,给学生提供展示逻辑推理和思维能力的平台,突出每个学生用自己的数学方式思考、探究,注重考查学生的创新意识和能力以及有理、有序、有度的思维品质,在问题探究中积累数学活动经验,提升数学探究能力,彰显数学教育对学生能力发展的价值. 图8 图9 1)用含α的代数式表示∠BFD. 2)求证:△BDE≌△FDG. 3)如图9,AD为⊙O的直径. ②当OF∶OE=4∶11时,求cosα的值. (2022年浙江省宁波市数学中考试题第24题) 分析本题以圆为背景,将圆的基本性质与三角形边角关系、三角形全等和相似、勾股定理、三角函数等核心知识融合在一起,蕴涵了函数思想、方程思想、转化思想、从一般到特殊等重要的数学思想方法,将重要的数学知识点和数学思维体现得淋漓尽致,层次分明,适度综合,让不同水平的学生都有充分展示数学水平与能力的空间,较好地发挥了试题的评价导向功能.第1)小题重基础,通概念,激活知识梳理,由主干条件提取信息:∠AFB-∠BFD=α.把握几何图形特征:∠AFB-∠BFD=180°,建立方程组求解.第2)小题重过程,通思维,引领理性思考,体现综合性,加强理性思维含量.从寻找目标中提取常用的解题经验,已知一边相等,通过平行线寻找角相等,结合等弧等图形结构特征得到角相等的条件,在第1)小题角度计算的自然衔接与相互关联中发现等腰△BEF、等腰△BDF、等腰△BFG,使之成为一个合乎逻辑的和谐结构. 第②小题重训练,通算理,培养运算能力,增加思维量,考查理解分析能力.求余弦值的方法比较常规,恰恰在常规解法基础上,设置了障碍,即不容易表示出这个角的邻边和斜边.在定性分析位置关系和定量确定数量关系的思维操作程序的指导下,只需设OF=4x,OE=11x,DE=DG=y,再用符号进行相关线段的数学表达即可. 图10 图11 思路2在前面发现等腰△BEF的指引下,如图11,作BH⊥AD于点H,即可表示出 利用△BDH∽△ADB列方程求解. 思路4由△FBE∽△FDB,得FB2=15x(15x+y),再利用双勾股BF2-FH2=BD2-DH2,问题迎刃而解. 本题坚持试题的应有开放度和综合性,实现了知识性、创新性与开放性的融合,理性思维——交相辉映,相得益彰;科学探究——传承创新,包容开放,以“谋求教学长远发展为”终极目标,促进学生全面素质的提高和教师专业的全面发展,引领教学进入良性循环的轨道.

3 立足主干,聚焦关键能力
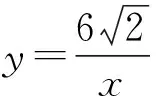


4 重视过程,体现数学本质

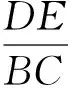
5 关注思维,凸显素养导向