且把金针度与人
——对一道初中数学学业考试题的探索与思考
魏祖成, 赵 涛
(1.竹溪县教师学习与资源发展中心,湖北 竹溪 442300;2.竹溪县实验中学,湖北 竹溪 442300)
2022年湖北省十堰市初中数学学业水平考试第9题是一道以圆内接四边形为背景的试题.对全县3 366位考生答题情况的统计分析引发了笔者对此题的较多思考,尤其是对学生中丰富的解题思路有了更多的了解,进而引发了笔者对数学教学工作进行探索与思考.
1 一题——真题呈现
例1如图1,四边形ABCD是⊙O的内接四边形,若∠A=90°,∠B=60°,BC=3,AD=2,则AB的长为
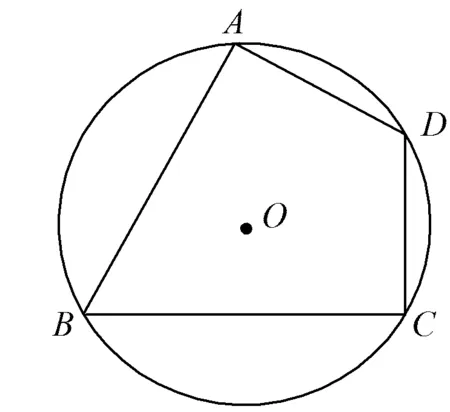
图1
( )
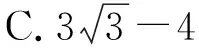
根据圆内接四边形的性质可知∠A=90°,则∠C=90°;由∠B=60°,可知∠D=120°.由此可知在四边形ABCD中,AB⊥AD,BC⊥DC,不妨称这种四边形为“双垂四边形”.它是一种特殊的四边形,在四边形“家族”中特别引人注目.
2 一课——解法探析
解答“双垂四边形”时要用到圆内接四边形的性质、含30°的“特殊”直角三角形的相关性质、勾股定理和解直角三角形相关知识.在已知和未知难以直接产生关系时,应采取“割”与“补”的办法添加辅助线,将其转化成熟悉的图形(如三角形、矩形、梯形等)来解答,考查了学生运用数学知识解决问题的能力[1].
2.1 延长增补法
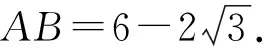

图2 图3
方法2类比方法1,延长BA和CD交于点E(如图3),下同方法1.
评注“双垂四边形”的两组对边都不平行,延长每一组对边都一定相交,那么该“双垂四边形”就是一个含30°特殊直角三角形的一部分.通过解“直角三角形”,所求问题便可迎刃而解.
2.2 垂线分割法
方法3过点C作CE⊥AB于点E,过点D作DF⊥CE于点F(如图4),则△BEC和△CFD都是直角三角形,四边形AEFD是矩形.在Rt△BEC中,BC=3,易得BE和CE的长度,易求EF的长度,进而可知CF的长度,故可求得AB的长度.

图4 图5
方法4过点A作AE⊥BC于点E,过点D作DF⊥AE于点F(如图5),则△ABE和△ADF都是直角三角形,四边形CEFD是矩形,易求AB的长.
方法5过点D作DE⊥DC交AB于点E,过点E作EF⊥BC交BC于点F(如图6),则△AED和△BEF都是直角三角形,四边形EDCF是矩形,易求AB的长.
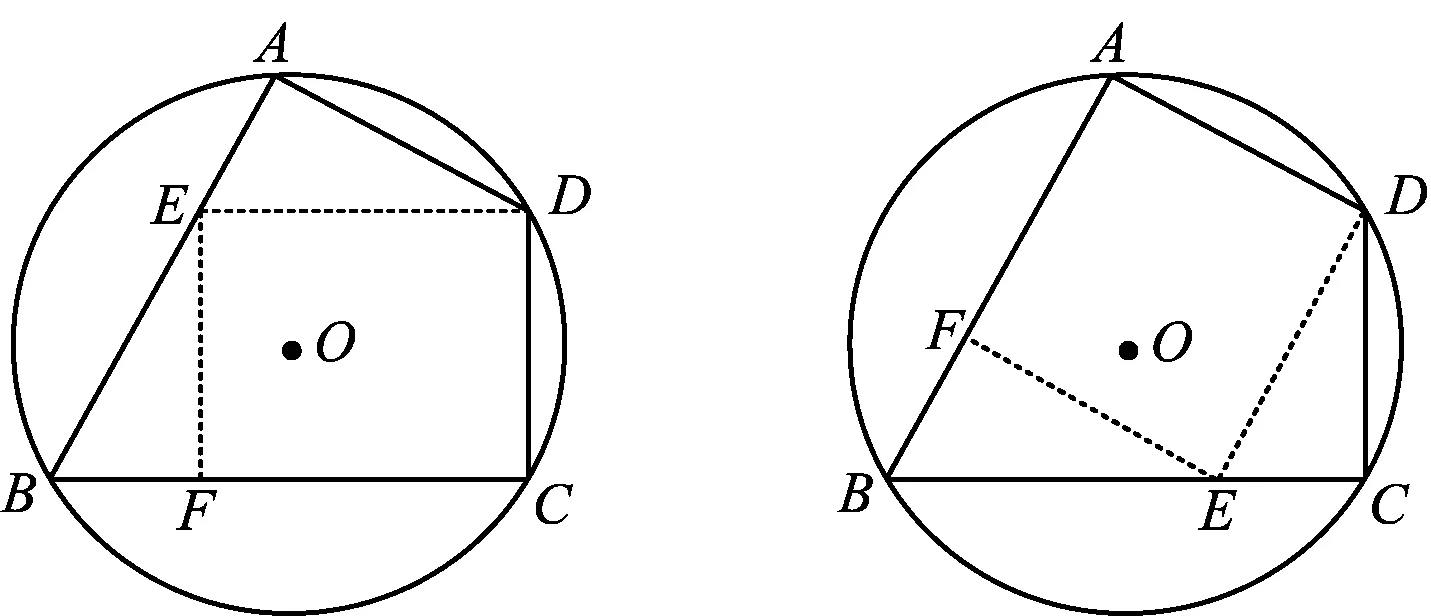
图6 图7
方法6过点D作DE⊥AD交BC于E,过点E作EF⊥AB于点F(如图7),则△CED和△BEF都是直角三角形,四边形EDAF是矩形,易求AB的长.
评注以“双垂四边形”中A,C,D为端点,分别引相应的“垂线”,把“双垂四边形”分割成直角三角形、直角梯形、矩形,这样就把问题转化为在一些“规则”的几何图形中来求解[2].
2.3 割补结合法
方法7过点B作BF⊥BC交⊙O于点F,联结DF,DF交AB于点E(如图8),则△AED和△EBF都是直角三角形,四边形BFDC是矩形,易知∠ADE=∠FBE=30°.在Rt△AED中,AE,DE可求,则EF可求;在Rt△EBF中,BE可求,故AB=AE+BE可求.
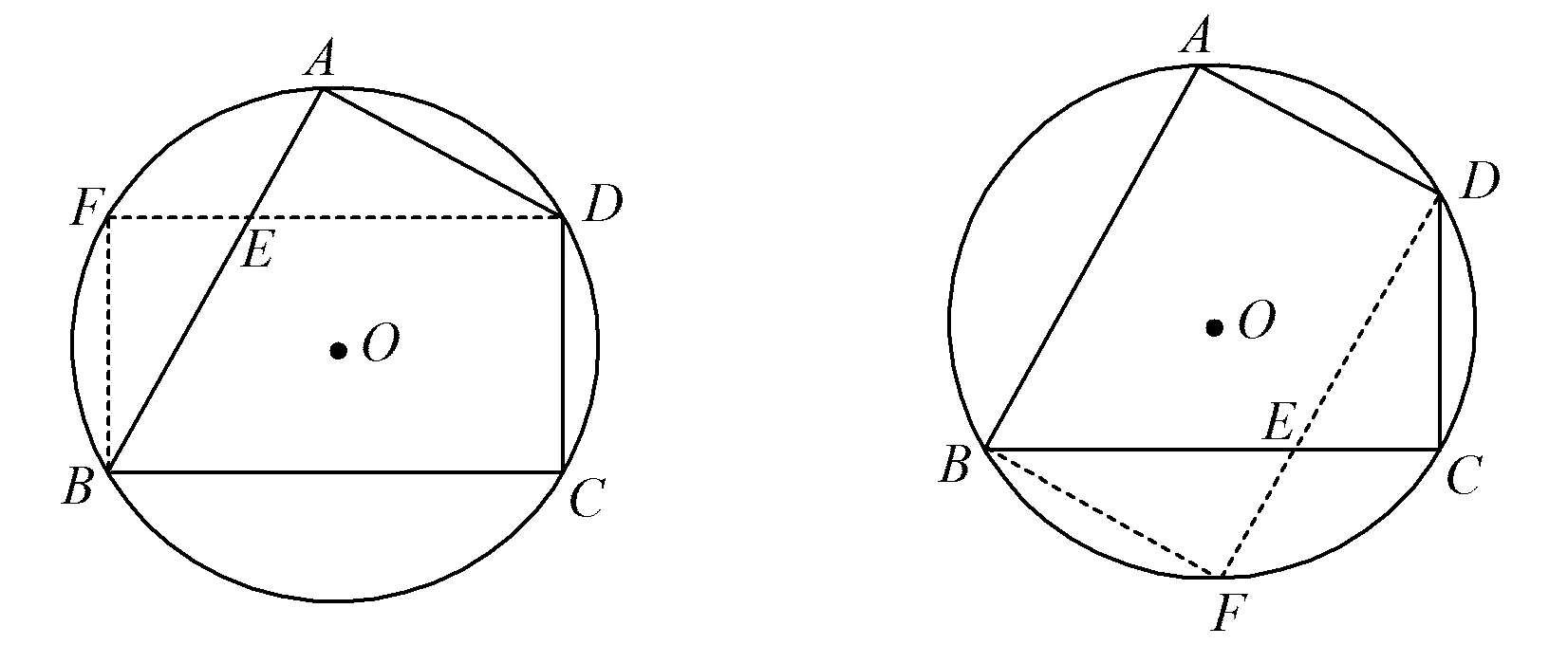
图8 图9
方法8过点B作BF⊥AB交⊙O于点F,联结DF,DF交BC于点E(如图9),则△BFE和△CDE都是直角三角形,四边形ABFD是矩形,易求AB的长.
方法9过点C作CE⊥AB于点E,过点C作CF⊥AD交AD的延长线于点F(如图10),则△BEC和△DFC都是直角三角形,四边形AECF是矩形,易求AB的长.
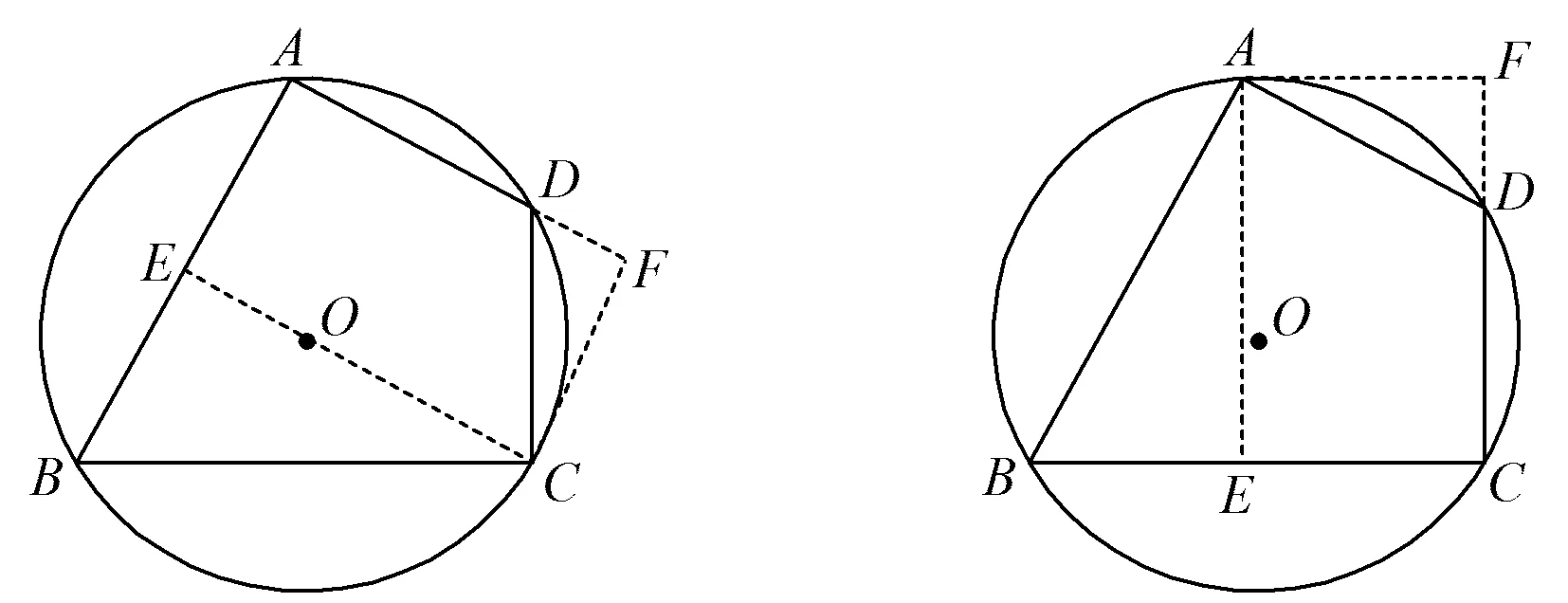
图10 图11
方法10过点A作AE⊥BC于点E,过点A作AF⊥CD交CD的延长线于点F(如图11),则△AEB和△ADF都是直角三角形,四边形AECF是矩形,易求AB的长.
评注通过作相应的“垂线”或“平行线”,在“双垂四边形”外部进行“补形”,使部分线段得到“平移”,把“双垂四边形”补成(或分割成)直角三角形、直角梯形、矩形,问题便可轻松获解[3].
2.4 翻转折叠法
方法11作AE⊥BC,垂足为E,作梯形ADCE关于AE的对称图形(如图12),点D,C的对称点分别为G,F,易求GD的长度,FC=GD,进而求得BE的长度,于是在Rt△ABE中易求AB的长度.

图12 图13
方法12作CE⊥AB于点E,作梯形CDAE关于CE的对称图形(如图13),点A,D的对称点分别为F,G,易求AB的长度.

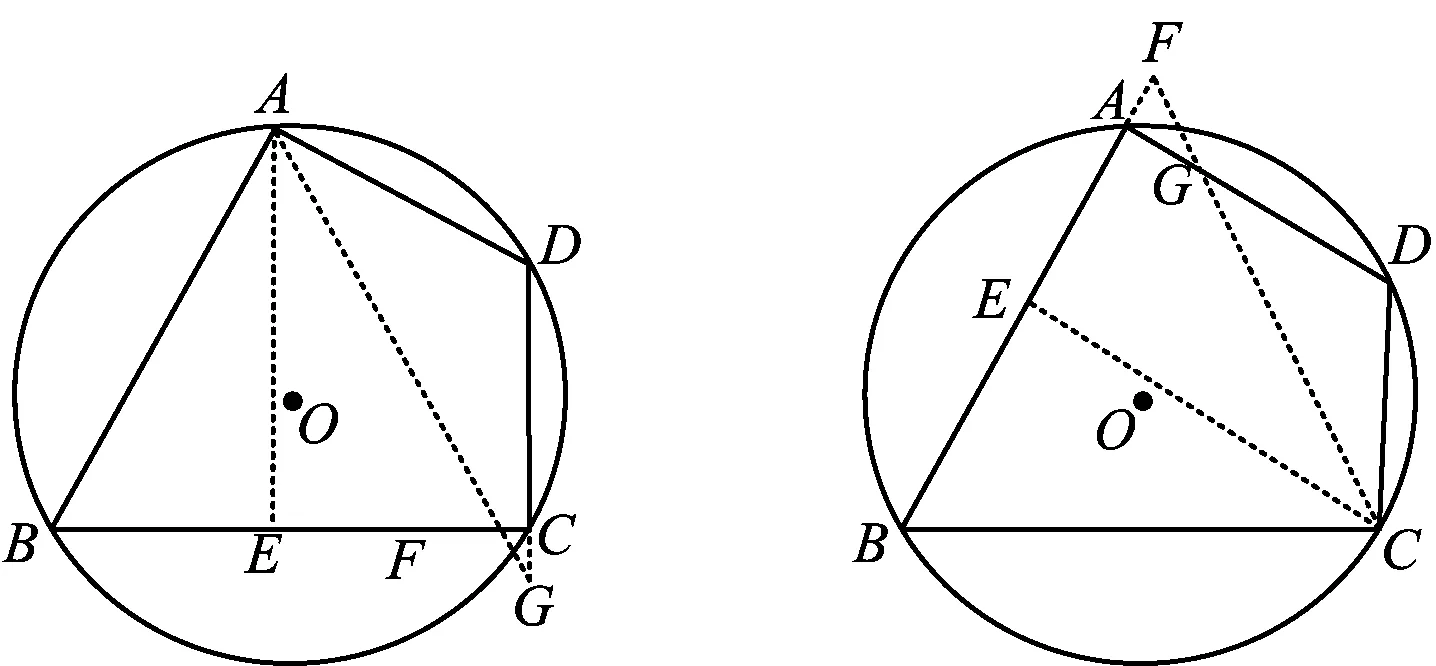
图14 图15
方法14作CE⊥AB于点E,作△BCE关于CE的对称图形(如图15),点B的对称点为F,联结CF交AD于点G,易知DC=DG,易求AB的长度.
评注对称图形给我们优美、有序、赏心悦目的感觉,利用轴对称图形可以将一部分图形进行对叠(或进行180°翻转),使已知和所求线段之间靠近一些,使所求问题轻松获解[3].
2.5 平移替换法
方法15过点A作AE⊥BC于点E,过点C作CF∥AD交AE于点F(如图16),则△ABE和△CEF为直角三角形,四边形AFCD是平行四边形,易求AB的长度.

图16 图17
方法16过点C作CE⊥AB于点E,过点A作AF∥CD交CE于点F(如图17),则△BCE和△AEF为直角三角形,四边形AFCD为平行四边形,易求AB的长度.
方法17过点D作DE∥BC,DF∥AB,交AB,BC于点E,F(如图18),则△AED和△DCF都为直角三角形,四边形BFDE是平行四边形,易求AB的长.
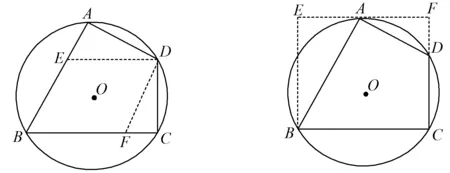
图18 图19
方法18过点B作BE∥CD,过点A作EF∥BC交CD的延长线于点F且BECF(如图19),则△AEB和△ADF都为直角三角形,四边形BCFE是矩形,易求AB的长.
方法19过点B作BE∥AD,过点C作EF∥AB交AD的延长线于点F且BEAF(如图20),则△BCE和△DCF都为直角三角形,四边形ABEF是矩形,易求AB的长.
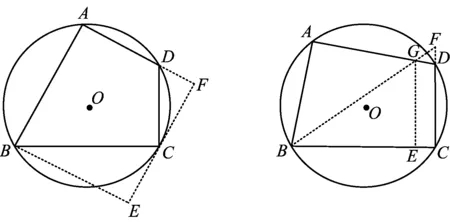
图20 图21
评注通过作相应的“平行线”,使部分线段得到“平移”,把“双垂四边形”分割成了直角三角形、直角梯形、矩形,问题便可轻松获解[3].
2.6 平分内角法
方法20作∠B的平分线交AD于点G,与CD的延长线交于点F,过点G作GE⊥BC于点E(如图21),则△ABG,△BCF和△BEG都为直角三角形,△DFG是等边三角形,易求AB的长.
方法21作∠B的平分线交AD于点F,与CD的延长线交于点E(如图22),则△ABF,△BCE都为直角三角形,△DEF是等边三角形,易求AB的长.

图22 图23
方法22作∠B的平分线交AD于点F,过点F作FE⊥BC于点E,过点D作DG⊥FE于点G(如图23),则△GDF,△BEF,△ABF都为直角三角形,四边形DGEC是矩形,易求AB的长.
方法23作∠D的平分线交BC于点F,交AB的延长线于点E(如图24),易求AB的长.
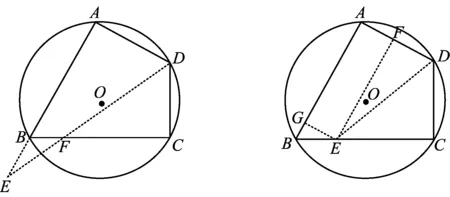
图24 图25
方法24作∠D的平分线交BC于点E,过点E作EG⊥AB于点G,过点E作EF⊥AD于点F(如图25),则△BEG,△EFD都为直角三角形,四边形AGEF是矩形,易求AB的长.
评注前面的解法中都没有破坏∠B和∠D的整体性,由于∠B=60°,∠D=120°,都可以视为“特殊角”,通过作∠B和∠D的“平分线”,从而构造含有30°角的特殊直角三角形,使问题解决十分轻松[3].
从上述添加辅助线的思考方法不难看出,充分利用了垂直、平移、旋转、翻折、对称等方法将图形划分成为熟悉的图形,从而使已知和未知之间产生联系,从不同的角度进行思考,就会产生不同的辅助线,殊途同归最终均会达到解决问题的目的.
3 一思——解题反思
3.1 变式
3.1.1 关于“角”的探究
1)∠B和∠D是“特殊角”.
在双垂四边形ABCD中,∠A,∠C是直角,∠B和∠D是两个“特殊角”,一般情况下∠B为60°,30°或45°,则∠D相应为120°,150°或135°,利用直角三角形中的角角关系、边边关系、边角关系,所求问题便会迎刃而解.
2)∠B和∠D是“任一角”.
在双垂四边形ABCD中,∠A,∠C是直角,∠B和∠D是两个“任一角”,同样利用直角三角形中的角角关系、边边关系、边角关系,利用解直角三角形的方法,所求问题便会迎刃而解.
3.1.2 关于“边”的探究
1)已知4条边中的任意两边,可求另外两边(∠B和∠D是“特殊角”或“任一角”).
如图26,在双垂四边形ABCD中,∠A,∠C是直角,4条边AB,BC,CD,AD中知其中一边不能解这个四边形,但知其中任意两边就可以解这个四边形.

图26
2)已知一边和直径,可求另3条边和∠A的平分线的长.
如图26,在双垂四边形ABCD中,∠A,∠C是直角,若AC平分∠BAD,BD=10,AB=6,求AD,BC,DC,AC的长.
3)已知夹∠A的两边长和直径,可求∠A的平分线与直径相交成的4条线段的长.
如图26,在双垂四边形ABCD中,∠A,∠C是直角,若AC平分∠BAD交BD于点M,AB=a,AD=b,BD=c,求AM,CM,BM,DM的长.
4)已知夹∠A的两边长,可求∠A的两边与∠A的平分线长的关系.
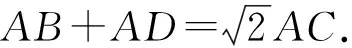
3.2 推广


图27
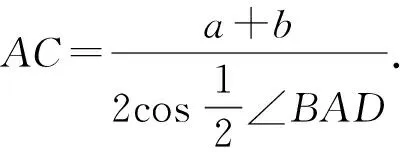
3.3 应用
如图28,在直角坐标系中,⊙O1经过坐标原点,分别与x轴正半轴、y轴正半轴交于点A,B.若⊙O经过点M(2,2),设△BOA的内切圆的直径为d,试判断d+AB的值是否会发生变化?若不变,请求出其值;若变化,求其变化的范围(答案:d+AB的值不会发生变化).

图28 图29
如图29,设△AOB的内切圆分别切OA,OB,AB于点P,Q,T,则
d+AB=OQ+OP+QB+PA=OA+OB.
在x轴上取一点N,使AN=OB,联结OM,BM,AM,MN.因为OM平分∠AOB,所以
∠BOM=∠MON=45°,AM=BM.
又因为∠MAN=∠OBM,OB=AN,所以
△BOM≌△ANM,
从而
∠BOM=∠N=45°,
于是
∠OMN=90°,
进而
故d+AB的值不会发生变化,其值为4.
3.4 反思
从此题丰富的解法思路和变式可以看出,在平时的数学教学过程中应加强对学生综合运用知识来解决问题的能力的培养.在今后的数学教学过程中要加强基础知识、基本技能和数学思想方法的教学力度,加强计算能力、思维能力、规范解题等方面的训练,让所有的学生都快乐地学习、健康地发展.

