基于“一题一课” 探析习题生长
——以一道九年级习题教学探究为例
许科挺, 毛孟杰
(海曙区集士港镇中心初级中学,浙江 宁波 315171)
众所周知,数学复习课具有数学知识系统化、基本技能熟练化、数学思想方法外显化等功能.浙教版《数学》教材中的复习课大多以“小结”和“目标与评定”的形式来呈现,其中“小结”主要罗列本章需要理解、掌握的基本知识与基本技能,“目标与评定”是以习题的形式来评估学生对基础知识和基本技能的掌握程度,以及学生综合运用知识解决实际问题的能力情况.事实上,复习课还可以用另一种课的形式——“一题一课”来演绎.“一题一课”就是教师通过对一道题或一个材料的深入研究,挖掘其内在的学习线索与数学本质,基于学情,合理、有序地组织学生进行相关的数学探究活动,以达成多维目标的教学过程[1].
由此可见,“一题一课”是一个由“题”化“课”、对教材素材进行“二次开发”的过程.这个过程需要教师找出适当的材料或题目,通过改编、组合、加工和延拓,设计出一个彼此相关的“习题链”,从而达成学生数学知识系统化、基本技能熟练化、思想方法外显化和综合运用知识解决实际问题的能力等多维目标.因此,“一题一课”的目标能否有效达成,很大程度上取决于“习题链”的设计是否具有针对性.本文以一道二次函数的习题为母题,通过全方位、多层次的思考与探究,设计出一个可生长的、涵盖初中数学主要知识点的习题链.
1 母题呈现
例1如图1,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A,B,与y轴交于点C(0,3),顶点为D(1,4),求抛物线的解析式及点A,B的坐标.
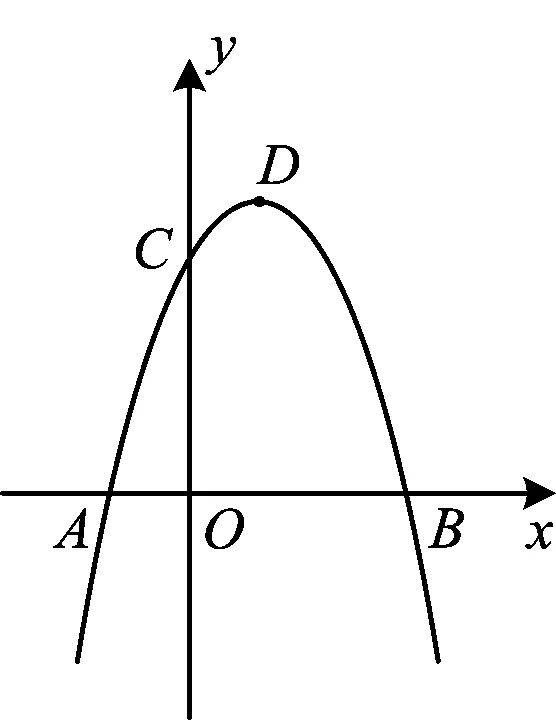
图1
(答案:y=-x2+2x+3,点A的坐标为(-1,0),点B的坐标为(3,0).)
功能分析母题是由浙教版义务教育教科书《数学)九年级上册第一章第3节“二次函数的图像”的一道课后作业题改编而成.本题的价值主要体现在以下两点:
1)从代数角度来说,要确定抛物线的解析式y=ax2+bx+c,应由3个条件确定,如抛物线经过3个点,或抛物线经过2个点和它的对称轴,或抛物线经过顶点和另一点.因此,由“抛物线经过顶点和y轴上的一点,求其解析式”的问题是一道常规题.解决这类问题的方法有一般式、分解式和顶点式3种.根据题目给出的条件,显然用一般式和顶点式较为合适,采用待定系数法列方程(组)来解决.因此,母题不仅能巩固学生的基础知识、基本技能和数学思想方法,还有利于培养学生的解决问题方法的选择意识,从而提高学生解决问题的能力.
2)从几何角度来说,题目中“抛物线与坐标轴的交点和它的顶点”的4个点构成四边形,坐标原点O与点C,A构成直角三角形,坐标原点O与点C,B构成等腰直角三角形,抛物线的顶点D与点A,B构成等腰三角形,整条抛物线是以“抛物线对称轴”为对称轴的轴对称图形.若让点或线段分别在抛物线上或抛物线的对称轴上运动,再结合相关的一些点和线段,就出现一系列有关长度、位置、相似、特殊图形存在性等问题.这就有利于教师在设计习题过程中,把初中数学中的“代数与几何”两个重要领域有机融合起来,从而达到“一题贯通一片”的目的.
2 习题生长
生长1周长与面积问题.
例2如图2,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A,B,与y轴交于点C(0,3),顶点为D(1,4).联结AC,CD,BD.

图2
1)求四边形ABDC的周长;
2)求四边形ABDC的面积.

设计意图我们知道,长度、角度和面积等是平面几何重要的研究对象.从求点的坐标深入到求图形的周长和面积,是母题不断深化的过程.学生在求四边形ABDC的周长时,应先通过勾股定理求出线段AC,CD和BD的长度,体现“数形结合”思想;在求四边形ABDC的面积时,需要把一般四边形进行分割,化成熟悉的直角三角形和直角梯形来解决,这较好地体现了数学中的“化归”思想.而数学思想实质上就是数学的“本质”与“精神”.
生长2函数与角度问题.
例3如图3,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A,B,与y轴交于点C(0,3),顶点为D(1,4).联结BD,在BD上方的抛物线上有一动点P,过点P作PH⊥x轴于点H,PH交BD于点Q,联结PB,PD,BC.设点P的横坐标为t,PQ的长度为s.

图3 图4
1)求s关于t的函数解析式;
2)当PD∥BC时,求s的值以及∠PBH的正切值.
1)解如图4,过点D作DE⊥x轴于点E,则
即
则
QH=6-2t,
从而
PQ=PH-QH=-t2+2t+3-(6-2t)
=-t2+4t-3,
于是
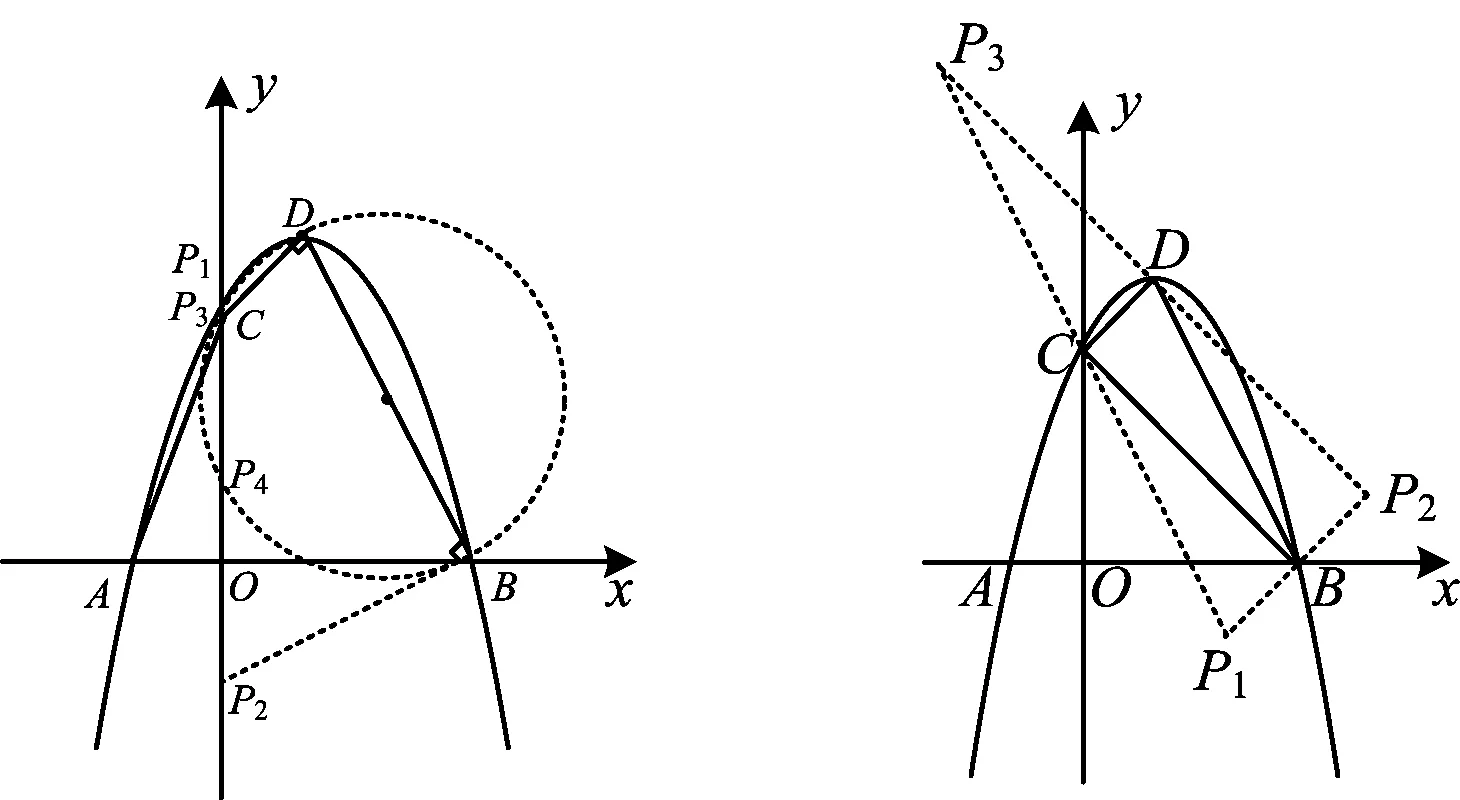
s=-t2+4t-3(其中1 2)欲求s的值,先求t的值. 方法1如图4,设DE与BC交于点M,PH与BC交于点N.由∠BOC=90°,OC=OB=3,知Rt△MEB和Rt△NHB都是等腰直角三角形,则 ME=EB=3-1=2, NH=BH=3-t, 从而 DM=DE-ME=4-2=2, PN=PH-NH=-t2+2t+3-(3-t)=-t2+3t. 由PD∥BC,PN∥DM,得四边形DMNP是平行四边形,则 DM=PN, 即 -t2+3t=2, 解得t=1(舍去)或t=2.下略. 方法2由PD∥BC得直线DP的斜率和直线BC的斜率相等,即 解得t=1(舍去)或t=2. 当t=2时, s=-t2+4t-3=-22+4×2-3=1, PH=-t2+2t+3=-22+2×2+3=3, BH=3-t=3-2=1, 故 设计意图由BD上方的抛物线上的动点P,引起PQ,PN,QN和NH等线段长度的变化,从而使图形由封闭走向开放、从静态走向动态.在两个变化数量之间探索彼此相互依存的关系,这就是数学中重要的函数思想.在探究s与t的函数解析式的过程中,用到锐角三角函数或相似三角形性质;在探求“当PD∥BC时,求s的值以及∠PBH的正切值”的问题中,用到了等腰直角三角形、平行四边形和直线斜率等性质.学生在用图形的性质来简化数学运算的过程中,有利于提升自身的逻辑推理能力和数学运算能力. 生长3全等与相似问题. 例4如图5,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A,B,与y轴交于点C(0,3),顶点为D(1,4).设M是抛物线上的点,过点M作MN⊥x轴于点N,联结AC与MB,若△MNB∽△AOC,求点M的坐标. 图5 图6 解由△MNB∽△AOC且∠MNB=∠AOC=90°,得 这样的点M有4处M1,M2,M3,M4,如图6所示.设点M的横坐标为t,则点M的纵坐标为-t2+2t+3. 1)对于点M1,有 M1N1=3BN1, 即 -t2+2t+3=3(3-t), 解得t=2或t=3(舍去).由 -t2+2t+3=-22+2×2+3=3, 知点M1的坐标为(2,3). 2)对于点M2,有 M2N2=3BN2, 即 -(-t2+2t+3)=3(3-t), 解得t=-4或t=3(舍去).由 -t2+2t+3=-(-4)2+2×(-4)+3=-21, 知点M2的坐标为(-4,-21). 3)对于点M3,有 BN3=3M3N3, 即 3-t=3(-t2+2t+3), 4)对于点M4,有 BN4=3M4N4, 即 3-t=-3(-t2+2t+3), 评注当点M的坐标为(2,3)时,△MNB≌△AOC. 设计意图三角形相似是平面几何中一种只要求保角的图形变换,而三角形全等可看做相似比为1的相似变换,它是一种要求既保角又保距的图形变换,因此全等与相似是几何中重要的图形变换.在探求符合“与已有的Rt△AOC相似的△MNB”的点M坐标中,由于涉及两个相似三角形直角边不同的对应关系和直角边MN的不同表示方法,学生在解题中需要用到“分类讨论”思想.“分类讨论”思想不仅是数学的本质,更是学生逻辑推理素养的一种具体表现. 生长4最值与定值问题. 例5如图7,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A,B,与y轴交于点C(0,3),顶点为D(1,4),P是抛物线对称轴m上的一个动点,线段PQ=1(点Q在点P的下方).分别联结CP和AQ,求CP+AQ的最小值. 图7 图8 解如图8,过点Q作QE∥PC交y轴于点E,则 CP=EQ,CE=PQ=1. 联结线段BE交直线m于点G,由于点A,B关于直线m对称,从而 AQ=BQ, 于是 CP+AQ=EQ+BQ. 欲求CP+AQ的最小值,只需求EQ+BQ的最小值.根据“两点之间,线段最短”得:当点Q与点G重合时,EQ+BQ的值最小,最小值为线段BE的长度.由点C的坐标为(0,3),CE=1,得点E的坐标为(0,2),从而 图9 证明设点M(x1,y1),点N(x2,y2),经过点M,N的直线解析式为 代入y=-x2+2x+3,整理得 由韦达定理,得 则 所以 生长5图形与存在问题. 例6如图10,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A,B,与y轴交于点C(0,3),顶点为D(1,4),问:在抛物线对称轴m上是否存在一点P,使△PBD是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由. 图10 图11 2)若BD=BP,则点P,D关于x轴对称,故t=-4; 3)若PD=PB,则 (4-t)2=(0-t)2+(3-1)2, 引申1把例6中的点P改为在y轴上,把“△PBD是等腰三角形”改成“△PBD是直角三角形”,其他条件不变,问:这样的点P是否存在?若存在,求出点P的坐标;若不存在,请说明. (答案:如图12,点P的坐标为(0,3.5)或(0,-1.5)或(0,1)或(0,3),使得△PBD是直角三角形.) 图12 图13 引申2在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A,B,与y轴交于点C(0,3),顶点为D(1,4),问:在平面上是否存在一点P,使得以P,B,C,D为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由. (答案:如图13,点P的坐标为(2,-1)或(4,1)或(-2,7),使得以P,B,C,D为顶点的四边形是平行四边形.) 设计意图学生探究特定图形是否存在的问题,属于探究性问题.它需要一定的构造方法,通过该类问题的解决能有效地发展学生的创新意识.例6和它的两个引申分别把所求的点放在抛物线的对称轴、y轴和平面上,探究等腰三角形、直角三角形和平行四边形是否存在的问题.学生解决这些题除了要用到等腰三角形、直角三角形和平行四边形知识外,还需要用到圆和线段中垂线的知识,更需要具备分类讨论思想和几何直觉能力. 笔者认为,教师要进行“一题一课”的习题设计,需要注意以下3个方面. 作为生长为“习题链”的母题,它的素材主要源自教材中的典型例题、习题、中考题或学生熟悉的学习与生活背景.这些素材由于较为经典或者广为学生熟知,素材也较为贴近学生现有的数学知识结构、学习经验和思维方式,因此它比较容易激发学生的兴趣,使学生进入积极参与探究活动的心理状态. 由收集得到的素材改编成为的母题,它应该具有习题的基本功能,比如母题既能有效考查学生的基础知识、基本技能和数学思想方法,又能提升学生解决问题的应用意识;它还应该具有潜在的生长功能,比如,母题由于具有良好的结构,因此可以适当改变它的条件,去探索结论的变化,或者给定一些特定的结论,去探索使结论成立的条件,或者它与数学其他领域相结合,在更大的空间中探求问题的变化等. 我们认为,在将母题设计出一个习题系列时,一般有以下3种方法:1)从简单到复杂.当母题具有可以深化探究的可能时,设计习题可以从“简单到复杂”.例如,例2是从母题结论中“抛物线与x轴的交点坐标”出发,与已知条件中的两点结合,设计出“探求四边形的周长与面积”的问题.2)从静态到动态.当母题条件处于封闭、静止状态时,设计习题可以“从静态到动态”.例如,母题中的抛物线、对称轴、顶点、抛物线与坐标轴的交点等都是静态的、确定的,我们在抛物线上设置动点和在对称轴上设置动线段,就出现了相应线段长度的变化,从而为探求变量之间的函数关系和相关量的最值问题提供了可能.3)从单一到多维.当母题条件较为单一时,设计习题可以“从单一到多维”.例如,母题中的条件仅有抛物线的顶点和其他4个定点,我们可以分别加上“平行”“相似”“等腰三角形”“直角三角形”和“平行四边形”等元素,使习题变得更有韵味. 设计好一系列习题后,接下去应关注习题之间的衔接,使之成为层次分明的“习题链”.习题之间的衔接,主要是数学知识间的衔接、数学思想方法间的衔接和思维层次上的衔接. 习题链设计要有针对性,有利于“一题一课”教学多维目标的达成.首先,每一道习题要有主干知识的考查,促使学生形成较为完备的数学知识体系;其次,习题要有重要数学思想的渗透,从而彰显数学精神;最后,习题更要有对学生核心数学素养的培养,尤其要突出对学生的逻辑推理、数学运算、几何直观等方面素养的提升[2].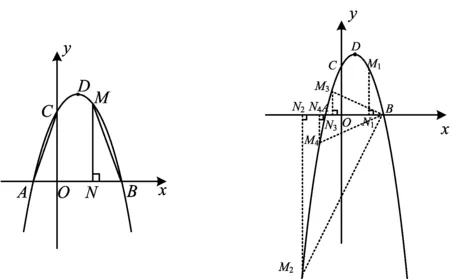

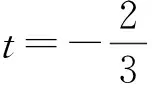






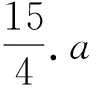

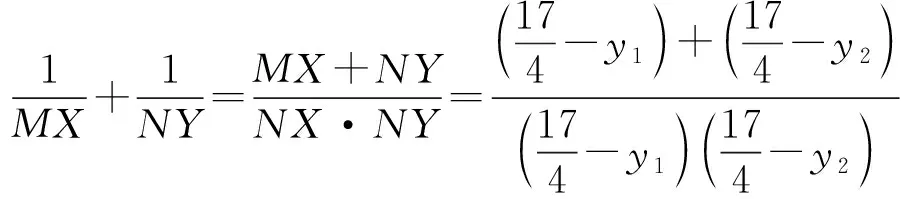




3 3点思考
3.1 注重素材收集,思辨母题功能
3.2 研究习题生长,关注题间衔接
3.3 彰显数学精神,提升数学素养

