2022年数学新高考Ⅰ卷第21题赏析*
2023-01-16 02:24福建教育学院数学研修部350025蔡海涛
中学数学研究(江西) 2023年2期
福建教育学院数学研修部 (350025) 蔡海涛
一、试题呈现
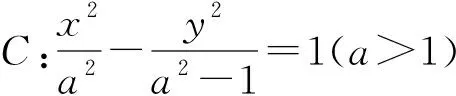
(1)求l的斜率;
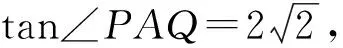
本题以双曲线为载体,考查直线的方程、双曲线的标准方程及其简单几何性质、三角形的面积等基础知识;考查运算求解能力,逻辑推理能力,直观想象能力及创新能力等;考查数形结合思想,函数与方程思想,化归与转化思想等;考查直观想象,逻辑推理,数学运算等核心素养;体现基础性、综合性与创新性.
二、解法赏析
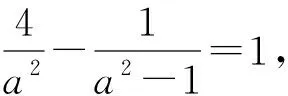
评析:把点A的坐标代入,易得双曲线的方程,由直线与双曲线联立,设而不求把直线AP,AQ的斜率之和用变量k,m表示,根据斜率之和为0,得直线l的斜率的值.

评析:根据双曲线的参数方程,把P,Q两点的坐标用参数表示,进而用参数表示直线AP,AQ的斜率之和,求得t1t2的值,整体代入得直线l的斜率的值.
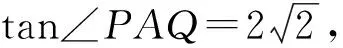

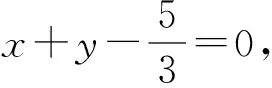
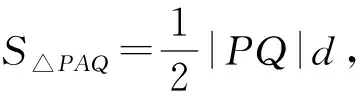
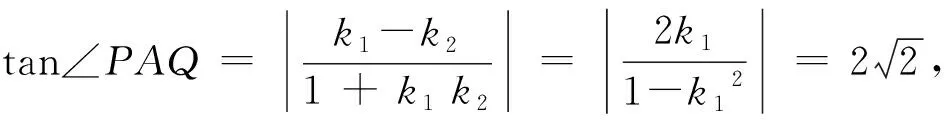
评析:涉及角的问题,考虑利用两直线的到角公式切入,求得直线AP,AQ的斜率,得直线AP,AQ的方程,与双曲线方程联立求得P,Q两点坐标.
三、解后反思
1.求圆锥曲线方程一般用待定系数法,涉及直线与圆锥曲线位置关系问题一般是联立,设而不求,再利用根与系数的关系整体代入.
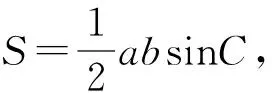
四、跟踪训练

(1)求双曲线C的标准方程与离心率;

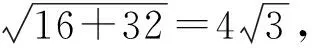
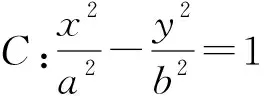
(1)求该双曲线的标准方程;
(2)设NA1和MA2交点为P,则△PF1F2的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
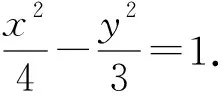
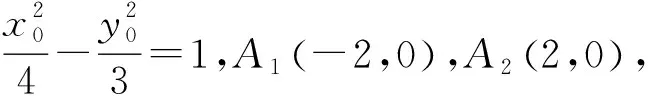
猜你喜欢
高中数理化(2022年3期)2022-03-14
物理之友(2020年12期)2020-07-16
中学数学杂志(2019年1期)2019-04-03
中学数学研究(广东)(2018年24期)2018-03-12
科技知识动漫(2017年8期)2017-08-09
中学生数理化(高中版.高二数学)(2017年1期)2017-04-16
福建中学数学(2016年7期)2016-12-03
光学精密工程(2016年1期)2016-11-07
电测与仪表(2016年6期)2016-04-11
中学数学杂志(2015年9期)2015-01-01

