考试命题视角下的试题探究——以空间中距离之和最小值问题为例

刘祥云，黄小燕

(江苏省兴化中学，江苏泰州，225700)

数学学习离不开试题的训练，但纯粹的刷题已无法适应新高考要求，数学试题探究活动是提升试题效能的一个重要手段.《普通高中数学课程标准(2017年版)》在对数学高考的考试命题说明中，要求在命题中，需要突出内容主线和反映数学本质的核心概念、主要结论、通性通法、数学应用和实际应用.在命题中，应特别关注数学学习过程中思维品质的形成，关注学生会学数学的能力.考试命题的视角主要是从试题的通性通法、高阶的数学思维、会学数学的能力三个方面来进行试题研究，旨在寻求试题研究的一般方法，引导学生深入思考试题的本质，丰富试题的内涵和外延，提升学生的学科核心素养.

1 试题呈现、代数试解

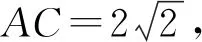
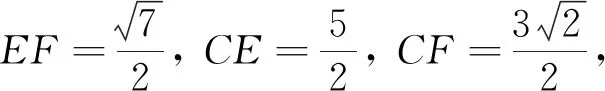
图1

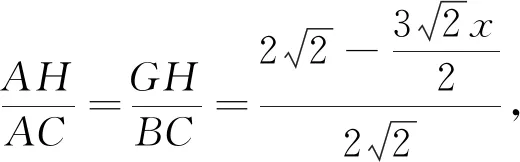
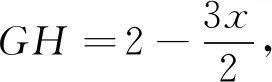
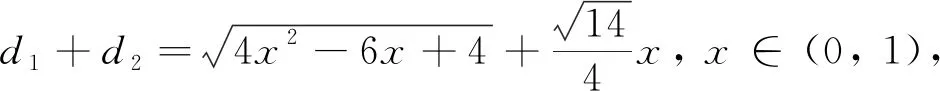
本题是2022年武汉二模试题填空压轴题最后一问(分值3分)，参考答案是建立空间直角坐标系，利用空间向量转化为代数问题求解，类似于解法1的求解过程(求导过程省略).空间向量是判断空间位置关系、计算空间距离、计算空间角的通性通法，若在考试过程中，试题所处的位置和分值，不适合计算量大的方法求解，若在平时的习题训练中，空间向量会掩盖空间想象能力，无法掌握图形与图形、图形与数量之间关系的基本方法，更加无法借助图形性质探索数学规律，达不到培养空间想象能力的要求.

2 本质探寻、另辟蹊径

图2

通过题海搜索，发现早在2006年，江西的高考(题目2)就已经考察过空间中两距离和的最小值问题.本题的解法可以从代数和几何两个角度来求解，代数方法就是用空间直角坐标系，设出点P坐标，利用距离公式表示出两线段之和，再用导数分析单调性求出最小值；几何方法是利用平面化的思想，将平面A1BC1和平面BCC1平移到同一个平面，在同一平面中利用余弦定理求出CA1的长度.从考试命题的角度看，命题者想要考查的是几何方法，通过特殊几何体的结构特征，进一步考查空间想象能力及平面化的思想.那么对于题目1，命题者是不是也有同样的意图呢？能否构造出两个新平面，从平面化的思想入手呢？

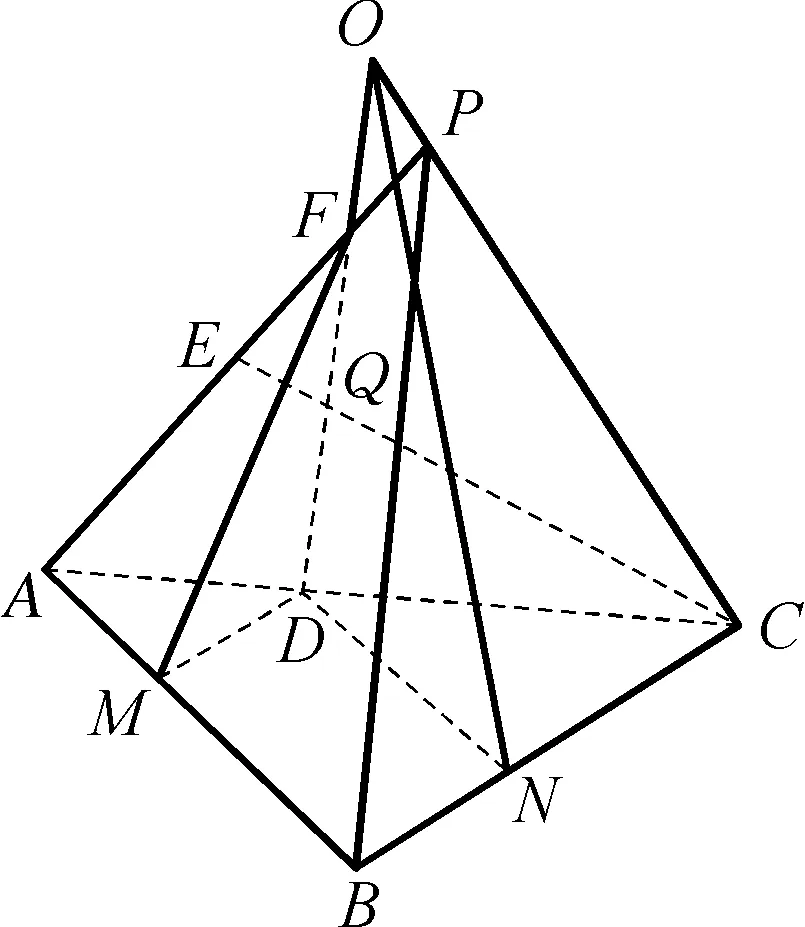
图3

图4

3 举一反三、提升思维

通过几何条件的融合运用，将平面化思想得到有效的迁移，几何方法的成功解决，降低了立体几何中距离、角等问题对空间向量的依赖程度，大大减少了计算量.在提高解题效率的同时，加深了对问题本质的理解，训练了数学思维的收敛性.为了进一步发展数学思维的发散性和广阔性，仔细审视几何条件，思考探究，又可以得到以下两种几何解法.

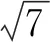
图5

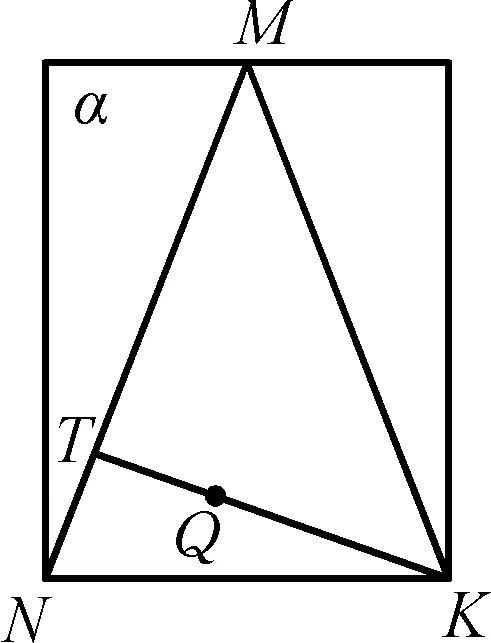
图6

解法3是空间问题中常见的“补形”思想，将不规则的几何体通过“割”或者“补”的方式变为规则的几何体.问题的解决，促进了学生数学关键能力的培养与数学思维品质的提升，一题多解，让学生掌握了解决相似情境下同类型问题的“高层次思维”，而这些“高层次思维”，使得“数学知识块”不断被强化，并纳入学生的记忆库中，成为认知解决的一部分.

4 命题探究，内化素养

数学核心素养并不是数学问题之间简单的叠加关系，数学学科核心素养是在数学问题解决过程中，提升数学思维，生成高阶思维，再次运用数学思维解决问题，再不断提升，再次运用提升的结果，总而言之，数学核心素养是在运用思维与提升思维不断联结融合的过程.命题探究就是提升核心素养的一种重要方式.每道题可以根据题根，仔细揣摩命题者的所想所思，思考问题的来龙去脉，认清问题本质.下面就以题目2为题根，揣摩一下命题者的意图，旨在提供一个提升素核心养的案例.(见下图)

改编思路在长方体ABCD-A1B1C1D1中题目条件解题思路分析打磨原因将题目2中立体图补充成长方体点P是BC1上动点,求PC+PD1的最小值最小值为CD1的长度题根模型将表面上的直线BC1换成空中间直线B1D点P是B1D上动点,求PC+PD1的最小值最小值为CD1的长度尽管点P由表面上的点变为空间中点,但是解题思维不变,计算难度下降将到两个定点距离换成一动一定F是AD1中点,P,E分别是B1D和A1B1上动点,求PE+PF的最小值E'为E关于直线BD的对称点,最小值为E'F的长度E,F变为一动一点,增加思维难度,可保留对称思维,将E,F点朝两个动点变化的思路将一动一定换成两个动点上下底面是正方形,P是B1D上动点,E是A1B1上动点,F是动平面ADD1A1上动点,求PE+PF的最小值由于该长方体是关于平面BDD1B1对称的,PE=PE'(E'为B1C1上的点),所以最小值为过E'作平面ADD1A1的距离,最小值即为边B1A1的长E,F点都变为动点,但本题最小值就是B1A1的长,故将平面ADD1A1换成一个斜平面将表面ADD1A1换成空间平面MND1A1上下底面是正方形,M,N分别是AB,CD的中点,Q是B1D与平面MND1A1的交点Q,P是B1Q上动点,E是A1B1上动点,F是动平面MND1A1上动点,求PE+PF的最小值由于该长方体是关于平面BDD1B1对称的,PE=PE'(E'为B1C1上的点),所以过E'作平行于ABB1A1的平面,与平面MND1A1相交于GH,过点E'作GH的垂线,垂足为F,最小值即为边E'F的长点P在QB上运动,条件不够简洁,可以将长方体截取部分,形成新的几何体,提炼条件,最终形成题目1