类比，让学生对抽象的知识掌握更容易——以《平方根》第一课时教学为例

丁 颖

(江苏省常州市戚墅堰实验中学，江苏常州，213000)

类比，就是借助于两类不同本质事物之间的相似性，通过比较将一种已经熟悉或掌握的特殊对象的知识推移到另一种新的特殊对象上去，从而对另一事物做出假定性说明的推理方法.本文从《平方根》的教学目标和教学过程设计入手，谈谈类比教学法在初中数学抽象知识中的应用.

1 “类比”在《平方根》教学中的应用

1.1 分析数学教学内容

本章在有理数和勾股定理等知识的基础上，进行数系的第二次扩张，引入无理数，将有理数扩充到实数范围，使学生对数的认识进一步深入.从有理数扩充到实数是第三学段数系扩张的最后一个阶段，中学阶段有关数的问题多是在实数范围内进行讨论的，同时实数也是一元二次方程、函数等后续内容学习的基础.

本节内容共计2个课时，本节课是第1课时，主要是平方根的概念和性质的教学.《义务教育数学课程标准(2022年版)》要求：对于数学概念的教学，要关注概念的实际背景与形成过程.

1.2 类比教学法的过程设计

(1) 与学生的生活经验和数学经验进行类比，引出本节课的“教学目标”

师：一个陌生人，你最想了解他(她)什么？重点了解他什么？最难了解的是他的哪方面？

学生：了解他(她)叫什么名字？了解他(她)与我们周围熟悉的人有什么关系？了解他(她)具有什么性格？最难了解的是他(她)的性格，需要漫长的过程.

师：说说看“平方根”知识，你想了解它什么？

学生互相说说，教师及时点拨引导到本节课的教学目标上.

(2) 与旧知识进行类比，引出平方根与平方互为“逆运算”

我们已经学习过哪些运算呢？它们中互为逆运算有哪些呢？

学生：加法、减法、乘法、除法、乘方等五种运算.加法与减法互逆、乘法与除法互逆.

师：乘方有没有逆运算呢？我们先来看下面的问题：

问题一：一个正方形边长为6厘米，那么这个正方形面积为——

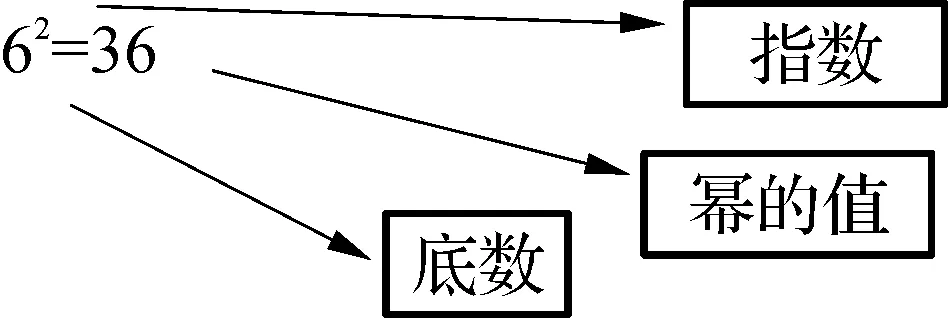
这是已知底数、指数，求幂的乘方运算.

问题二：如果一个正方形的面积为100平方米，那边它的边长为多少？

解：设正方形边长为X米，则

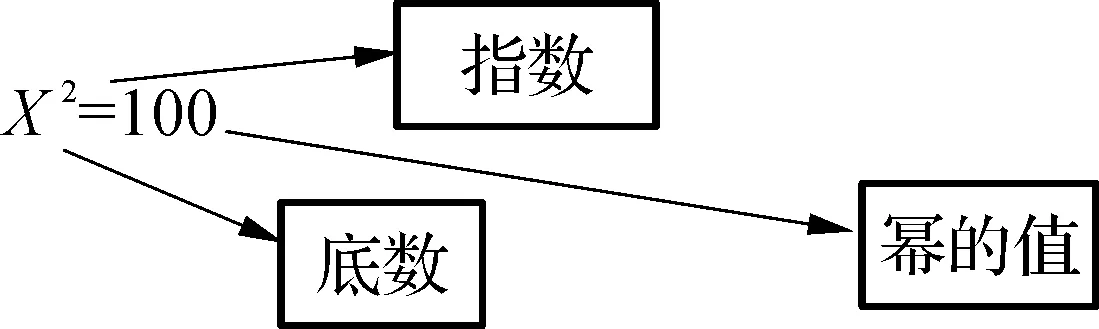
这是已知指数和幂，求底数的问题.正与上面的乘方运算相反，我们虽然不知道这是什么运算，但我们通过口算很容易求出X=10.

(3) 将“树根”“草根”等生活中事物名称与平方根概念进行类比，引入平方根的概念

我们来看下面的问题：

探索 发现

设计目的：这是引入平方根概念的切入点，要让学生充分地进行思考和比对.知道“两个互为相反数的平方等于同一个数”，为平方根的引入作准备.

(4) 概括：x2=a(a≥0)

因为x2≥0，所以a≥0，求x就是帮a找源头，即帮a找根子，是什么数平方得到a的？

类比：树有树根，草有草根，要知道是什么根子，就看根子上方长什么梢子.

因为x的右上方指数是2，所以x是a的二次方根，也就是说x是a的平方根.

平方根概念：如果x2=a(a≥0)，那么x叫做a的平方根.

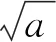
根号的书写：先写左边勾号，写好被开方数后，再写上面的一横.

平方根史话：以古希腊数学家毕达哥拉斯的守旧与其学生西伯斯的创新进行类比，让学生了解根号的由来，激发学生勇于创新，不局限于已有结论.

(5) 与生活中人的“戴帽”进行类比，讲解如何求一个非负数的平方根

这个定义，可以简记为：一数平方根，根号头上戴，正负莫丢掉.

开平方：求一个数平方根的运算，叫开平方.

(6) 开平方与乘方类比，理解新旧知识之间的区别和联系

开平方是已知指数和幂，求底数，与平方运算正好相反，所以开方与乘方是互为逆运算.由于平方与开平方互为逆运算，因此可以通过平方运算来求一个数的平方根，也可以通过平方运算来检验一个数是不是另一个数的平方根.

求一个数的平方根方法：

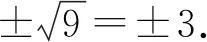
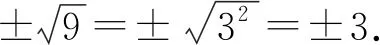
练习1：0.09的平方根记作

i.被开方数是完全平方数的开平方方法：被开方数要出来，先变完全平方数，去掉平方去根号，符号写在底数旁.

ii.被开方数不是完全平方数的开平方方法：不能写成平方数，根号里面长期住.

练习2：41的平方根是多少呢？

④ 因为？2=-36，“？”不存在，因此负数没有平方根，所以-36没有平方根.

通过分类讨论，使学生对有理数的平方根有一个全面的认识，进一步深化了平方根的概念，加深了对符号意义的理解和对平方根概念的灵活应用，这是平方根知识的重点和难点.

2 类比教学材料的编写与制作方法

2.1 类比前的准备环节

在这个环节中，主要是促使学生发散思维，在原有的知识结构中寻找与新知识(靶问题)匹配的类比源，也就是我们所说的“源问题”.这个过程应该让学生主动搜寻建构，但所用时间较长，容易误入歧途，或者根本找不到类比源.可能学生在以往的学习过程中没有这种类比的思维习惯，也不知道如何搜寻类比源.为了让学生顺利找到类比源，教师必须发挥好主导作用，通过设计问题串来引导学生找到相应的类比源.如本节课我设计了以下问题，串起本节知识点：① 与学生的生活经验“了解一个陌生人”进行类比，引出本节课的教学目标；② 与旧知识进行类比，引出乘方与开方互为“逆运算”，理解它们之间的区别和联系；③ 与“树根”“草根”等生活中事物名称与平方根概念进行类比，引入平方根的概念；④ 以古希腊数学家毕达哥拉斯的守旧与其学生西伯斯的创新进行类比，让学生了解根号的由来，激发学生勇于创新，不局限于已有结论.⑤ 与生活中人的“戴帽”进行类比，讲解如何求一个非负数的平方根.

2.2 类比的实施环节

类比，最核心的目标就是找到“有效的类比条件”，顺利实现由旧知识向新知识的类比.所谓“有效的类比条件”，就是类比实施的突破口，找到它就相当于找到了一把打开类比大门的钥匙，这是类比实施的中心环节，也是类比教学的难点.为了突破这个难点，就需要教师对数学知识本身的体系要有较为深刻的认识，对各部分知识的内在逻辑联系有充分地了解，善于发现知识间的类比关系，做好长期的学习、思考和积累.

2.3 类比结果的验证

并不是每种形式的类比都需要有此过程，有很多情况，此环节就已经蕴含在类比实施的过程中了.对于类比结果的验证有两点好处：一方面可以检验类比的正误，重新判断一下这个类比的可信度；另一方面，如果类比是正确的，通过验证可以进一步加深学生对新知识的理解，从而达到巩固类比所得到新知识的目的.

2.4 多元评价

课堂上要对学生在学习过程中所学知识效果情况进行评价.这种评价不断指导着学生的情感态度和价值观，指导着学生的学习方法和策略，保证教学目标的顺利实现.

一方面，可以进行学生之间的自评和互评.课堂上每学完一个知识点我就让学生进行自评和互评一次，培养学生的自尊心和正确评价自我的能力，提高其自信心.评价标准就是根据回答的准确性和回答的速度分为A、B、C三等.学生通过自评和互评可以发现自己在学习过程中所取得的成绩和不足，不断地调整自己.

另一方面，可以进行教师评价.学生的自评和互评，都必须与老师的评价结合起来，在对学生进行评价时，教师的作用是展示优秀学生的学习方法和评价方法，帮助学生学会自评.多采用一些鼓励性的评价语言.教学评价能够帮助教师及时掌握学生的学习情况，便于修改或调整教学活动计划，获得更加理想的教学效果.