少数民族地区文化资源融入高中数学教学的案例研究

孙雪梅，包广啟

(1. 曲靖师范学院教师教育学院，云南曲靖，655011 2. 云南省曲靖市第二中学，云南曲靖，655000)

《国家中长期教育改革和发展规划纲要(2010—2020)》明确指出：“加快民族教育事业发展，对于推动少数民族和民族地区经济社会发展，促进各民族共同团结奋斗、共同繁荣发展，具有重大而深远的意义.”数学教育在促进学生智力发展和形成理性思维方面具有独特的、不可替代的重要作用，但因为数学学科的抽象性、严谨性，数学语言的形式化特点，数学思维的特殊性，以及不同的历史文化经济背景，导致少数民族地区的数学教育水平与发达地区相比还有一定差距.

统一的、以主流文化以及汉语言思维习惯为背景的国家课程忽略少数民族学生所处的历史文化背景和思维模式，现行教材所提供的问题情境、实例等对他们来说都是不太熟悉的，使得少数民族学生在学习中面临着“文化冲突”的问题，也给他们的数学学习造成了困难[1].因此，如何结合当地文化资源，积极开发和有效利用各种文化资源来补充和衔接现行数学教材，使少数民族学生借助熟悉的当地文化情境进行数学学习，从而提高少数民族学生数学学习的兴趣，提升数学课堂教学的效益是值得少数民族地区教师思考的问题.

文章第一作者参加曲靖市高中数学教师课堂教学比赛的评委工作，听了第二作者任教的人教版(A版)高中数学必修第一册第四章第二节的“指数函数的概念”一课，受到启发，在他的教学设计的基础上，尝试将楚雄彝族自治州的地方文化资源融入此节课.现将教学过程设计的主要环节呈现出来，对于问题和例题的解答，教材中已有详细解答，就不再呈现.

1 教学案例及设计分析

1.1 引入文化资源，衔接教材

情境一：万家坝古墓群位于楚雄市城南的青龙河畔，是周朝时期的古墓葬遗址.1975年，云南省文物工作队对遗址进行了清理发掘，共发掘79座古墓.出土的随葬品有兵器、生产工具、生活用具、乐器、装饰品等文物共1 245件，其中青铜器1 002件，尤以5件铜鼓最为珍贵，被命名为“万家坝型铜鼓”(如图1所示).经“碳-14测年法”测定，铜鼓距今已有二千六百年左右，是迄今为止科学发掘所获铜鼓中最早的铜鼓.它在研究铜鼓的起源和发展、我国鎏金技术的产生和发展、我国古代五声和七声音阶的形成发展以及我省滇青铜文化的历史等方面有着重要的意义和参考价值.

图1 万家坝型铜鼓之一

根据情境一中的相关史料，教师说明：考古中经常会使用“碳-14测年法”来测定文物年代.“碳-14测年法”是根据生物体死亡后停止新陈代谢和该生物体中碳14的衰变程度来推算生物体死亡年代的一种测量方法.然后，教师提出问题：生物体死亡后，其体内的碳14的量衰变的规律是什么呢？请大家阅读课本第115页的《阅读与思考》，并思考课本第113页的问题2.

设计意图：教师结合当地考古史料，通过对“万家坝型铜鼓”及其在历史及科学研究中的重要意义和价值的介绍，自然引出 “碳-14测年法”， 无缝衔接教材.这不仅增强了数学教学的针对性，而且将地方文化渗透到数学课堂教学中，增强了学生的自豪感.

1.2 模型建立，概念抽象

问题一：当生物死亡后，它机体内原有的碳14含量会按确定的衰减比率(简称为衰减率)衰减，大约每经过5730年衰减为原来的一半，这个时间称为“半衰期”．按照上述变化规律，生物体内碳14含量与死亡年数之间有怎样的关系？

问题1：生物死亡后体内碳14含量的年衰减率p是多少？

解：略.

问题2：求出生物体内碳14含量y随死亡年数x变化的函数解析式？

解：略.

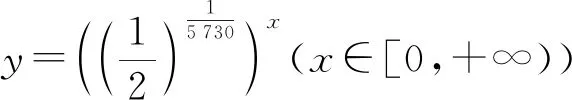
情境二：呈现楚雄州的旅游风景名胜资源：楚雄世界恐龙谷旅游区(如图2所示)、元谋土林(如图3所示)等风光照.

图2 楚雄世界恐龙谷

图3 元谋土林

根据情境二，自然引出课本中的问题1作为探究问题二.

问题二：随着中国经济高速增长，人民生活水平不断提高，旅游成了越来越多家庭的重要生活方式．由于旅游人数的不断增加，楚雄世界恐龙谷旅游区(A地)、元谋土林(B地)两景区自2001年起采取了不同的应对措施，A地提高了景区门票价格，而B地则取消了景区门票．

设计意图：结合当地旅游资源，找到与教材中问题1联系的结合点，顺势引入问题二，符合学生的实际生活背景，并且也让学生有亲切感和代入感.这开启了良好的开端，为后面的数学作铺垫，起到了“未谱曲调先有情”的效果.

1.2.1 发现和提出问题

问题3：假如你是地方政府工作人员，面对游客人数的变化，你该关注什么问题？

解：略.

设计意图：将学生代入角色，引导学生发现和提出问题，巧妙引出探究A、B两种方案对应的游客人次的年增长量问题.紧紧围绕教材内容，但又不拘泥于教材，步步为营，将学生置身问题情境中，激起学生的求知欲和认知冲突.

1.2.2 建立和求解模型

呈现教材中的数据(如表1所示)：A、B两地景区2001年至2015年的游客人次及逐年增加量．

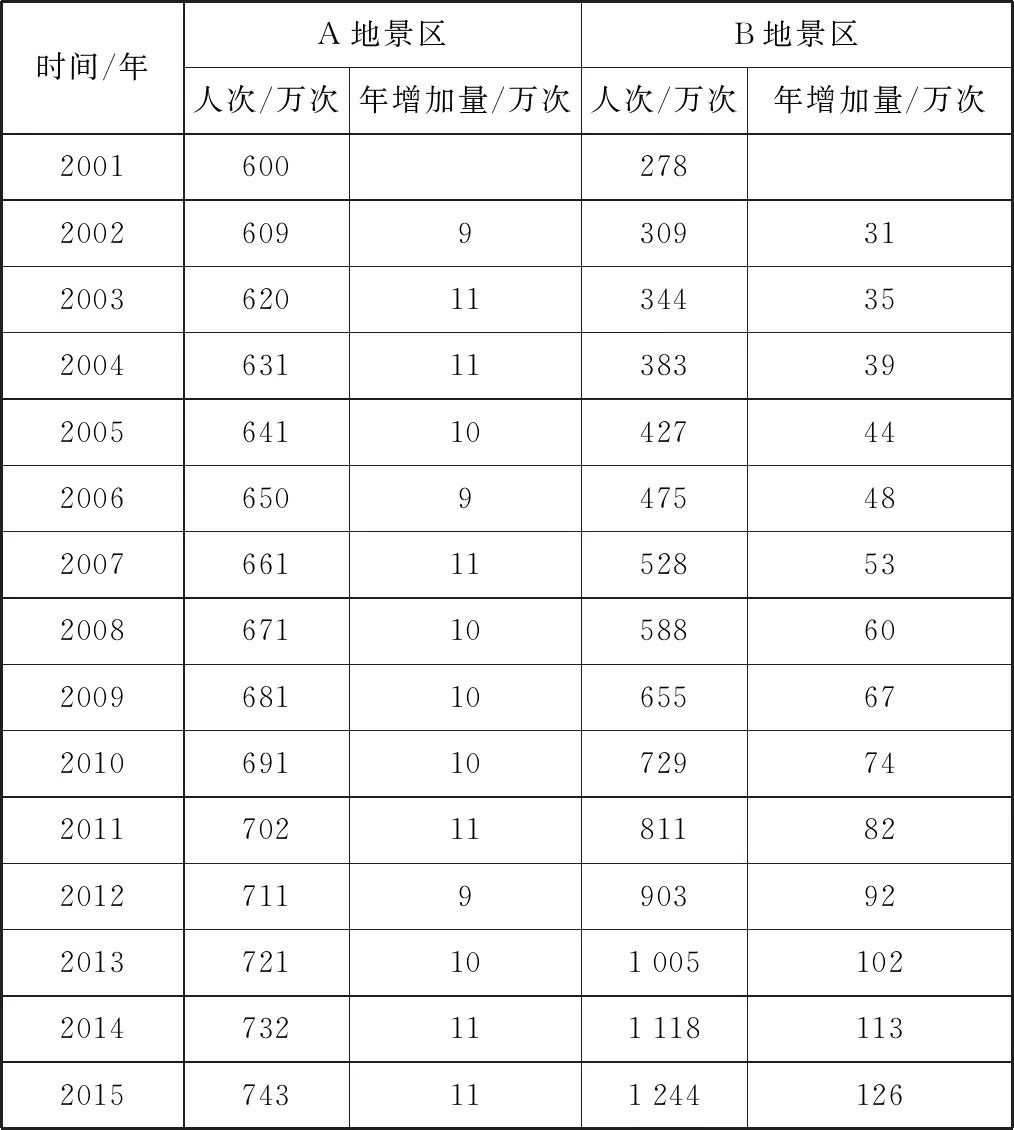
表1 A、B两地景区2001年至2015年的游客人次及年增加量

引导学生通过对数据的观察和分析，试着去比较A、B两种方案对应游客人次的年增长量并发现规律.

问题4：比较两地景区游客人次的变化情况，你发现了怎样的变化规律？

引导学生利用数形结合的方法探寻规律.根据上表分别画出A，B两地景区采取不同措施后15年的游客人次变化图象.

解：略.

设计意图：引导学生观察图4可以得出A地景区游客人次近似直线上升，年增加量约为10万次，为后面的例3中求图4的函数解析式f(x)奠定基础；观察图5可以看出B地景区游客人次为非线性增长，年增加量越来越大，用现有的知识求不出图5的函数解析式，为接下来探求此函数解析式埋下伏笔.

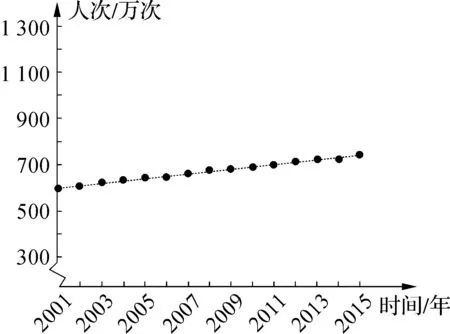
图4

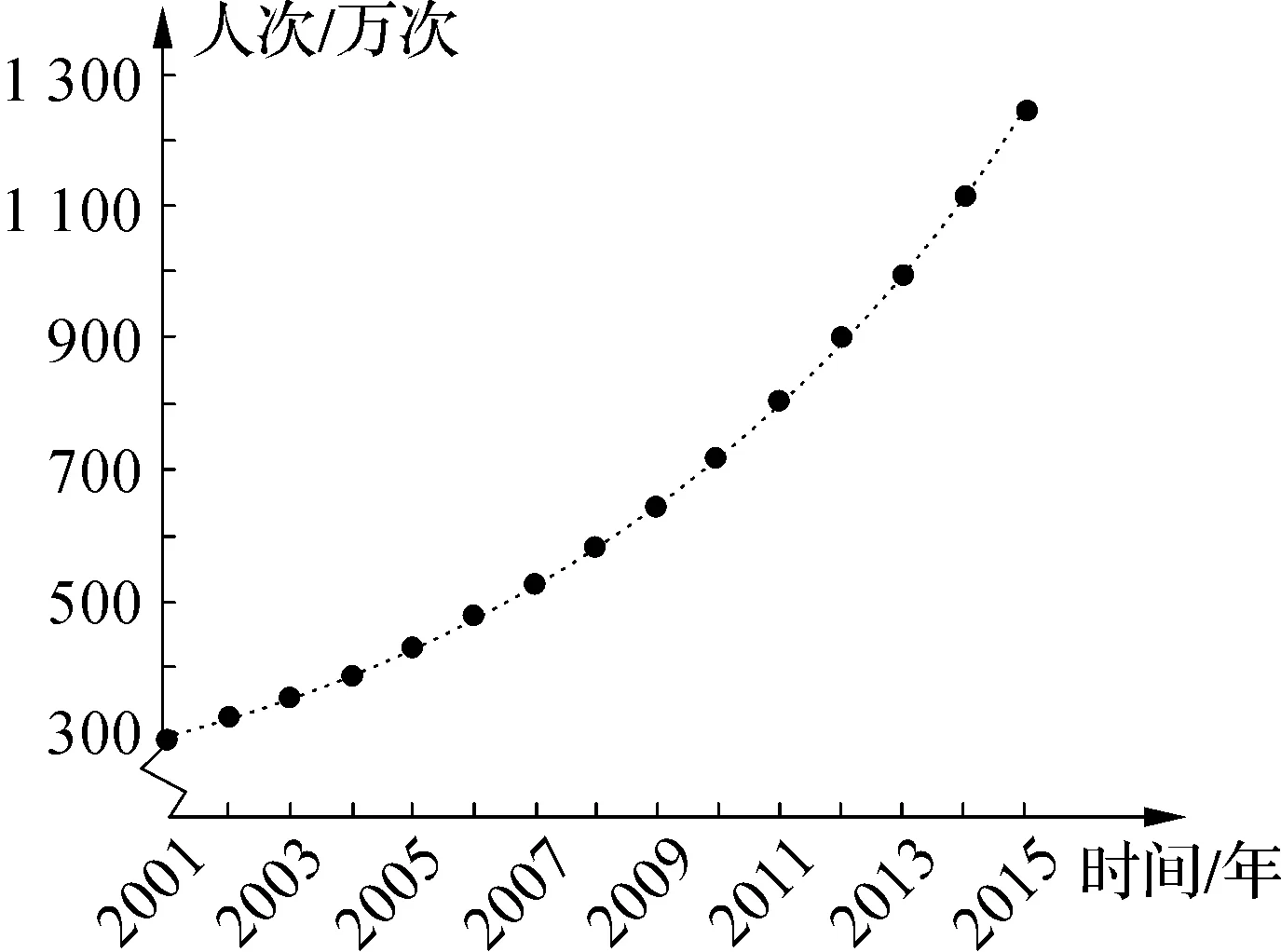
图5

问题5：求出图5的函数解析式.

引导学生分组探究：通过对B地景区每年的游客人次做相应的运算(一些组做减法，一些组做除法)去发现游客人次的变化规律，从而建立相应的数学模型描述出此变化规律.最后，通过学生的探究能找出刻画图5的函数解析式：y=1.11x(x∈[0,+∞)).

解：略.

设计意图：A地有相同的增长量(年增加量大致为10万次)，但B地游客增长量不同，不能凭借增长量求出B地游客人数y与年数x的关系式，应该寻找相同的量(增长率)来刻画图5的函数解析式.通过分组探究，让学生掌握做减法可以得到游客人次的年增加量，做除法可以得到游客人次的年增长率.增加量、增长率是两个很重要的刻画事物变化规律的量.

1.2.3 指数函数概念的引入

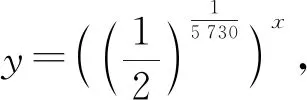
结合这两个函数解析式的求解过程，教师引导学生思考：这两个函数刻画了哪类运动变化现象？决定这类运动变化现象的要素是什么？要素之间的相互关系如何？可以用怎样的数学模型来刻画？然后，归纳这两个函数的共性，并指出指数x∈R时ax(a>0，且a≠1)有意义，从而给出刻画这类现象变化规律的函数的定义：

一般地，函数y=ax(a>0，且a≠1)叫做指数函数，其中指数x是自变量，定义域是R．

让学生自主探究问题6.

问题6：指数函数定义中为什么规定a大于0且不等于1?

设计意图：引导学生观察两个函数解析式的共同特点，抽象出指数函数定义，并通过对指数函数定义中底数a的范围探究，让学生感悟抽象思维、分类讨论的数学思想.结合函数解析式：y=1.11x(x∈[0,+∞))的求解过程分析，让学生理解指数函数刻画的现实事物变化规律的关键词是“增长率为常数”，发现规律的方法是做除法运算.这为后续学生懂得哪些实际问题可以通过建立指数函数型来解决做好铺垫.

以上教学围绕两个情境(情境一、情境二)及一系列环环相扣的问题链(三个大问题(问题一、问题二、问题三)和6个小问题(问题1—问题6))的探究，使教学不再仅仅停留在指数函数概念的知识表层，而且深入到知识产生过程中所嵌入的思想、方法与思维，并赋予知识和问题文化内涵，使学生在主动学习和探究的过程中，积累了分析和解决问题的经验，使其数学建模、数学抽象、数学运算、直观想象等数学核心素养得以提升.

1.3 概念巩固，模型应用

1.3.1 指数函数概念的理解巩固

例1判断下列函数是不是指数函数：

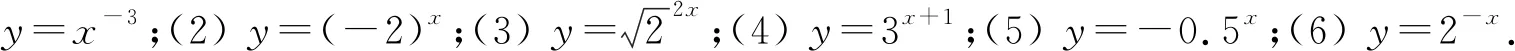
总结：.

例2已知函数f(x)=ax(a>0，且a≠1)且f(3)=π，求f(0)，f(1)，f(-3)的值．

解：略.

设计意图：通过辨析指数函数和求解指数函数解析式及其函数值，强化对指数函数概念的理解.

1.3.2 应用指数函数模型分析和解决问题

进一步呼应情境一及问题一，引导学生进一步利用指数函数模型分析和解决问题.

例3(1) 在学习活动一中，某生物死亡后，过了10 000年，它体内碳14的含量衰减为原来的多少倍？

解：略.

进一步呼应情境二及问题二，引导学生进一步利用指数函数模型分析和解决问题.

(2) 在学习活动二中，如果平均每位游客出游一次可给当地带来1 000元门票之外的收入，A地景区的门票价格为150元，设经过x年，游客给A，B两地带来的收入分别为f(x)和g(x)，请求出f(x)和g(x).

解：略.

(3) 在(2)的基础上，请比较这15年间A，B两地旅游收入变化情况．

解：略.

设计意图：利用指数函数模型进一步解决与问题一和问题二相关的问题，让学生进一步了解指数函数的实际意义，从而加深对指数函数概念的理解和应用.同时引出形如y=kax(k∈R，且k≠0，a>0，且a≠1)的函数是刻画指数增长或指数衰减变化规律的常用函数模型.

在以上例题讲解的基础上，让学生自主完成以下练习题：

楚雄市2020年底人口为63万，人均住房面积为46 m2，计划2025年底人均住房达到50 m2，如果该市将每年人口平均增长率控制在1%，那么要实现上述计划，这个城市平均每年至少要增加住房万m2.(精确到整数，注：1.015≈1.05)

解：略.

设计意图：利用指数函数型模型，进一步解决和学生家庭相关的实际问题，培养学生的应用意识，帮助学生切实感受数学与现实世界的联系，认识数学在社会、科学、经济等领域的作用，发展学生数学建模素养，提高实践能力，进而让学生逐步学会用数学语言表达世界.

2 思考和建议

数学教育与历史文化密切相关，不同的文化导致不同的教与学.少数学民族学生在主流文化中学习面临的困难是由文化冲突和文化差异造成的[2].文化背景凝聚着民族智慧和文化烙印[3].把地方文化资源从“文化学术形态”转化为“教育形态”，将地方文化(特别是民族文化)引进数学课堂，既扩大了学生的数学学习资源，又能使学生体验到数学就在身边，能增强学生对民族文化的认同和民族自豪感，还利于激发少数民族学生数学学习的兴趣和自信心.

我国少数民族文化多姿多彩、特色鲜明、形式多样，具有浓郁的地域特色.在其历史发展进程中，他们创造了大量有价值的文化、艺术、科学等文献典籍，建造了富有民族特色的建筑，产生了绚丽多彩的民俗文化，它们或源于生产实践，或源于宗教信仰，或源于活动仪式，或源于居住环境和服饰等.少数民族地区的数学教育工作者要以文化为视角，从当地少数民族族源文化、传统文化和现代旅游、休闲文化中，搜集整理其民族的宗教、天文历法、建筑、服饰、科技、工艺等民族文化文献典籍、实物等，从中整理和挖掘民族文化资源，得到第一手鲜活的民族文化资料.然后，在对民族文化中数学文化的挖掘的基础上，将这些文化资源结合主流数学教材编写相关教学案例，并应用于数学课堂教学和地方、校本课程资源开发中.

现行数学教材不可能满足各民族地区多种文化背景的教育需求.如何在具有浓厚和丰富文化底蕴的地方(民族)文化中选择和开发符合民族学生生活环境、思维方式、数学学习的素材和文化资源融入数学课堂教学？这对民族地区的数学教育工作来说，是值得思考的问题.以上案例只是在现行数学教材中的情境、实例、问题中寻找衔接少数民族地区学生的生活经验和文化背景的契合点的一些尝试，借此抛砖引玉，让更多数学教育工作者能参与其中，为提升少数民族地区的数学教育教学质量贡献自己的智慧！