在变式教学中挖掘题根——以一道“数列”课后习题为例

西华师范大学数学与信息学院 梁 燕 吴明忠 陈清方

万尔遐老师曾经说过：题根是一道具有生长性的题. 题根将学生救出“题海深渊”，提高解题效率，减轻学生负担[1]. 数列作为高考中必考的知识点. 涉及的相关题型变化多端，计算纷繁复杂，但看似杂乱无章的问题背后，事实上有通法可寻. 古人云：“万变不离其宗.”由于题根是题目的根基，因此研究题根对解题而言显得尤为重要.

1 原题呈现

已知Sn是等比数列{an}的前n项和，S3,S9,S6成等差数列，求证：a2,a8,a5成等差数列.

思路1：化归思想、方程思想.

分析：由于涉及等比数列前n项和，所以首先分类讨论公比q是否为1，根据前n项和的定义，分析出S9和S6中都包含了S3，再根据等差数列性质(等差中项)与等比数列通项公式列方程，求出公比q，代入需要求证的式子中，从而验证结论.

证明：①当q=1时，由Sn=na1，得

2S9=18a1，S3+S6=3a1+6a1=9a1.

所以2S9≠S3+S6.

故S3,S9,S6不成等差数列，应舍去.

②当q≠1时，因为S3,S9,S6成等差数列，有2S9=S3+S6，所以

2(S3+a4+……+a9)=S3+(S3+a4+a5+a6).

故2S3+2(a4+……+a9)=2S3+(a4+a5+a6).

即2(a4+……+a9)=a4+a5+a6.

所以2(a4+a5+a6)+2(a7+a8+a9)=a4+a5+a6，a4+a5+a6+2(a7+a8+a9)=0.

又因为a7+a8+a9=q3(a4+a5+a6)，所以

(a4+a5+a6)(1+2q3)=0.

又因为a4+a5+a6≠0，所以1+2q3=0.

由此可得

所以2a8=a2+a5，即a2,a8,a5成等差数列.

思路2：整体代换法、分析法、方程思想.

分析：同思路1先分类讨论公比q是否为1，再根据等比数列前n项和公式以及等差数列的性质(等差中项)列出等式，约分化简后运用分析法，观察化简后的式子与待证明的式子之间的关系，发现两式相差a1q-2倍. 思路2的特点是整个计算过程中并不用求出公比q，其巧妙之处在于运用分析法发现待证明等式和化简出来的等式之间存在特定的倍数关系从而找到此题的突破口.

证明：①当q=1时，同思路1.

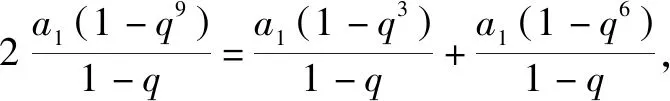
2(1-q9)=1-q3+1-q6，

2q9=q3+q6.

等式两边同时乘a1q-2,得

2a1q7=a1q+a1q4.

所以2a8=a2+a5，即a2,a8,a5成等差数列.

点评：思路1结合代入验证利用化未知为已知思想，中规中矩；思路2结合逆向思维利用设而不求的整体代换思想，非常巧妙，为后面的变式奠定了基础. 两种处理方法殊途同归，都运用了性质法，分类讨论思想、方程思想，培养了学生数学运算、逻辑推理等核心素养.

2 变式探究

原题所考查的知识点如表1所示，下面从条件和结论两方面入手，对此题进行变式探究. 数列题所包含的基本量有：首项a1、公差d(或公比q)、具体项第n项an、第n项的序号n、前n项和Sn等[2]. 由于此题涉及到的基本量较少，因此主要研究项的下标以及前n项和的下标这两种变式思路.

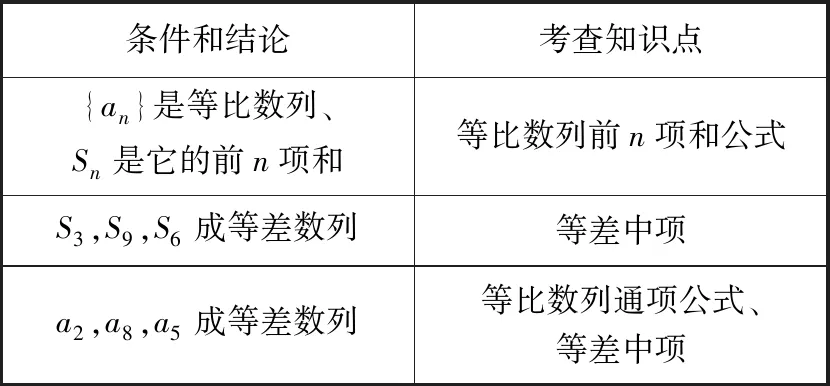
表1 原题所考查的知识点

2.1 条件变式探究

结论不变，条件改变下标：

S3,S9,S6→S1,S7,S4/S2,S8,S5/Sn,Sn+6,Sn+3.

变式1已知Sn是等比数列{an}的前n项和，S1,S7,S4成等差数列，求证a2,a8,a5成等差数列.

思路：引导学生逆向分析，由于条件改变，根据等差中项的性质得到的等式可变为2S7=S1+S4，化简得到2q7=q+q4，比较它与特征式的异同之处，发现等式两边同时乘a1，可以得到2a1q7=a1q+a1q4，于是证明出a2,a8,a5成等差数列.

变式2已知Sn是等比数列{an}的前n项和，S2,S8,S5成等差数列，求证a2,a8,a5成等差数列.

思路:等式2q8=q2+q5两边同时乘a1q-1.

变式3已知Sn是等比数列{an}的前n项和，对任意n∈N*，Sn,Sn+6,Sn+3成等差数列,求证a2,a8,a5成等差数列.

思路:等式2qn+6=qn+qn+3两边同乘a1q1-n.

2.2 结论变式探究

条件不变，结论改变下标：

a2,a8,a5→a1,a7,a4/a3,a9,a6/am,am+6,am+3.

变式4已知Sn是等比数列{an}的前n项和，S3,S9,S6成等差数列，求证a1,a7,a4成等差数列.

思路：由于条件不变，因此由已知条件得到的等式2q9=q3+q6不变，引导学生利用原题的解决方法(根据在等式两边同时乘a1q-2便可得证)，因此为我们提供了解题思路，等式两边同时乘a1q-3就能证明a1,a7,a4成等差数列.

变式5已知Sn是等比数列{an}的前n项和，S3,S9,S6成等差数列，求证a3,a9,a6成等差数列.

思路:等式2q9+q3+q6两边同时乘a1q-1.

变式6已知Sn是等比数列{an}的前n项和，对任意m∈N*，S3,S9,S6成等差数列，求证am,am+6,am+3成等差数列.

思路:等式2q9=q3+q6两边同时乘a1qm-4.

3 题根探究

在上述两种变式思路的基础上，可以发现下标之间存在特定的联系，结合由特殊到一般的数学思想方法，将条件结论结合在一起进行变式，拓展到更为一般情况.

变式7已知Sn是等比数列{an}的前n项和，对任意n,m∈N*，有Sn+1,Sn,Sn+2成等差数列，求证am+1,am,am+2成等差数列.

思路：由变式教学过渡到题根教学的过程中，教师切忌“填鸭式”教学，而应充分发挥学生的主观能动性，根据前面的变式循序渐进地引导学生自主找出规律，总结方法，提炼题根.培养学生的数学抽象素养和归纳能力.(等式2qn=qn+1+qn+2两边同时乘a1qm-n-1.)

变式8已知Sn是等比数列{an}的前n项和，对任意p,r,t,k,m,n∈N*，且p,r,t成等差数列，若pSk,rSm,tSn成等差数列，求证pak,ram+1,tan+1成等差数列.

思路：由于新添加了系数这一基本量，具有一定的难度.教师可以适当给出题根分析，即此题根是在讨论已知含有系数的任意三个前n项和为等差数列，去判定任意三项亦为等差数列的问题.证明方法与前面类似，此处不再作具体的分析．

4 教学反思

荀子曰：“千举万变，其道一也．”意思是万千事物尽管在形式上变化多端，但其本质是不变的[3]. 在解决千变万化的数学题的过程中，要注意观察分析其变化规律，在变与不变中抓准其本质的不变性，还原数学知识的本来面目，从而开展变式教学.

变式教学是一种双赢的教学手段， 既能培养学生在变换的条件下举一反三，又能挖掘出题目的本质，有利于学生了解知识方法的拓展和迁移，从而掌握这一类题型. 因此教师在变式教学中，应抓住问题本质，精选题、巧设计、有意识地寻找和设置题根，开展围绕题根知识的变式教学.