新课标背景下高中数学教学活动化的实践与思考

河北省固安县第一中学 王春艳

俗话说：“兴趣是学习最好的老师.”不论是教学活动化，还是活动教学化，都是以激趣为出发点，以具体的教学任务为核心，围绕教学目标设计教学过程.数学教学中，常见的活动包括游戏、问答、角色扮演、访谈等形式，丰富的活动为学生提供了更多参与、实践与表达的机会，拉近师生、生生距离的同时，还能促进学生思维的飞速发展.

然而，活动再好，都只是教学的一种手段，伴有思维升华的活动才是有深度的教学.笔者以一节复习课教学为例，浅谈在新课标背景下教学活动化的实施过程与思考，共勉！

1 开放问题，激发兴趣

良好的开端是成功的一半，不论课堂教学内容是什么，在学生感兴趣的基础上开展教学才能高效完成教学任务.复习课具有知识点多、杂、综合性强等特点，该怎样激发学生主动参与学习的热情呢？如何利用活动来梳理、巩固学生的知识网络结构？这是笔者一直在思考的问题.

例1已知a+b=1，且a>0，b>0.根据这个条件，说一说自己第一反应的结论，并思考如何添加待求解的问题.

本题虽然题干简短，但开放性问题却给学生提供了一个宽阔的思维空间.学生在勇敢的表达中，获得自信；又在板演中，充分暴露思维过程，增强自信.这样的教学活动，不仅激发了所有学生的参与热情，还让每个学生在自己的能力范围内思考、探索，最终达到知行合一、全面发展的目的.

2 穷追不舍，优化思维

思维的发展遵循由浅入深的特征，而教学活动化的主旨就是从浅显、有趣的活动中，探寻知识的内涵，获得思维的成长[2].为了优化学生的数学思维，在以上教学基础上，教师根据学生的实际认知水平，展开追问，以培养学生思维的深刻性与发散性.

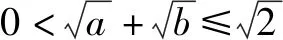
此过程可看出猜想对学习产生的影响，良好的猜想、预估不仅体现了一种重要的学习习惯，还凸显了学生认知的生长点.

追问2：a2+b的取值范围是什么？

此追问的目的，在于提醒学生关注变量间存在的约束关系，同时再次肯定第一个提出a=1-b,b=1-a这个想法的学生，揭示该结论中所蕴含的消元思想.同时也反映出变量间的约束关系，对挖掘问题中所存在的隐含条件产生的影响.此追问不仅强化了学生对函数定义域的认识，还有效地培养了学生思维的严谨性.

追问3：对于本题的条件，还能从哪些角度去解读？

引导学生从不同视角去思考问题，是教学活动化秉承的宗旨.此问鼓励学生换个角度看待并思考问题，有效地促进学生知识的横向发展，这也是培养学生发散性思维的良好途径.

针对此问，有学生提出：根据a+b=1联想到直线，那么所约束的范围则对应的是一条线段，a2+b2即可解读为距离的平方.

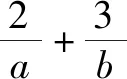
学生的思维被打开后，分别从不同的角度来分析此问.连续的追问，不仅拓宽了学生的视野，还深化了学生对数学各个分支之间联系的认识，起到融会贯通、提高思维品质的成效.

3 深入探究，强化理解

深入探究是实现教学活动化的关键因素.从解一道题中发现解一类题的方法，让无序的问题转化成具有可操作性与规律性的有序模式，是教学深入探究的目的，更是培养学生形成深刻性思维的重要途径[3].随着教师的引导，学生从众多问题中抽象出它们的共性特征，为形成良好的解题技巧作铺垫.

要求学生带着如下几个问题进行探究：①思考本题所提供条件的知识背景，有哪些与之相关的重要方法与结论？②从题设条件中，你发现了哪些表示量与量关系的词语？③根据结论，你联想到哪些问题？

在这几个问题的引导下，学生很快回答出：本题有向量背景，与之相关的有向量共线条件、加减运算、坐标表示、重心、数量积等，由此联系到坐标法、基向量、几何意义及特殊化方法等.

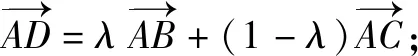
学生在自主探究活动中，体会“向量→几何→代数”互相转化的关系，并获得用变量来表达其转化过程的方法.把条件、方法与结论三者放在一起分析时，可用文字、图象、符号语言进行相互转化，这是解题的关键.

4 变式拓展，灵活应用

变式拓展主要是通过题设条件的改变，让问题变得更为深入、发散.教师可将问题中具有相关性的元素，从不同角度进行改变，让各个元素凸显出不同的功能，让学生能更加立体化、多维度地去分析并解决问题.

如例2，在问题探究结束后，笔者则提出新的变式，引发学生产生新的思考.

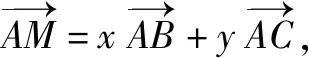
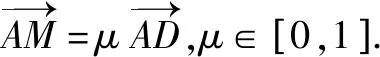
到此处，学生的思维出现了障碍.笔者让学生思考：到现在为止，出现了几个变量？应从什么角度去考虑？

随着教师的点拨，有学生立即想到两个变量，从它们的相关性着手，通过消元法即可突破这个障碍.由0≤μ≤1，得0≤μ≤2μ-λμ≤2μ≤2.

从以上教学活动过程来看，变式的应用，将学生的思维从无序问题过渡到有序问题的思考中，第一种方法凸显了函数思想，第二种则突出了数形结合思想在解题中的优势.此过程，学生充分体会到从不同角度思考同一个问题的乐趣.

总之，新课程标准不仅强调了学生的主体性地位，还强调了教师的引导作用.本节课的教学，教师不仅给予了学生充足的时间与空间进行探索与交流，还充分发挥了教师的职能，在适当的时候给予巧妙的引导，让学生感受教学活动化带来的乐趣，为学生数学核心素养的形成与发展奠定了坚实的基础.