强化解题研究 提升思维能力

甘肃省甘谷第一中学 刘兰生

数学解题及其研究一直是教师教学与学生学习中的一个重要过程．历年的典型高考真题，都是数学解题研究的一大活字典，利用高考真题的典型性、基础性、综合性、应用性和创新性，强化解题研究，探究教学艺术，挖掘问题本质，拓展规律结论，摒弃题海战术，全面提升学生的解题能力、创新能力、综合能力以及思维能力等，以及教师的教学水平与研究能力．下面结合一道2021年高考真题的解题研究加以剖析、展开、应用．

1 巧展高考题

A．0 B．1 C．2 D．3

2 夯实基本功

常规解法最能体现学生的数学基本功，是学生审题后第一时间内自然而然想到的、常见的破解方法之一，也是学生解题经验的积累与应用的充分体现．夯实基本功，是教师教学与学生学习中最基本的要求之一.因此，要不断强化基础训练，全面提升学生的“四基”水平，提升解题能力．

解法1：基本不等式+特殊值法.

利用基本不等式，可得

以上三式同向相加，整理可得

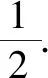
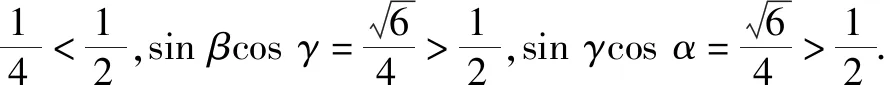
综上分析，可知满足条件的个数的最大值是2.故选择答案：C．

点评：解法1是比较容易想到的破解方法之一.首先利用基本不等式确定三个值之和sinαcosβ+sinβcosγ+sinγcosα的取值范围，确定所求个数的上限；然后利用特殊角的选取，通过求值直接确定满足题意的个数情况；最后综合判断满足条件的个数的最大值．基本不等式与特殊值的结合，方法基本，双管齐下，一张一弛，巧妙判断．

3 培养探究欲

解法2：二倍角公式法.

以下部分同解法1.

点评：利用三个三角代数式相乘处理，结合三角恒等变换中的二倍角公式加以变形，借助三角函数的有界性确定其积式的最大值，结合不等式的性质确定三者不可能同时满足条件，得以合理推理与论证．

解法3：主元法.

利用辅助角公式，可得

sinαcosβ+sinβcosγ+sinγcosα

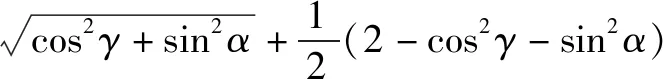
(令u=cos2γ+sin2α)

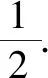
以下部分同解法1．

点评：利用三个三角代数式相加处理，结合辅助角公式对其中两个和式进行变形与转化；利用三角函数的图象与性质、基本不等式加以转化，引入参数，把对应的三角关系式转化为涉及参数的二次函数问题；通过配方处理，结合二次函数的图象与性质确定其和式的最大值，结合不等式的性质确定三者不可能同时满足条件，得以合理推理与论证．

解法4：反证法.

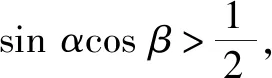
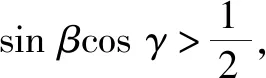
则α>β，β>γ与γ>α矛盾，故假设不成立.

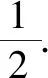
以下部分同解法1．

解法5：排序不等式法.

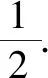
以下部分同解法1．

点评：利用三个不相等锐角的一般处理方法，确定对应的大小关系，进而得到对应的正弦值与余弦值的大小关系；利用排序不等式中“乱序和小于等于同序和”建立不等关系式，结合三角恒等变换公式加以变形与转化；再利用三角函数的图象与性质确定其和式的最大值，结合不等式的性质确定三者不可能同时满足条件，得以合理推理与论证．

事实上，在数学解题过程中，强化解题研究，充分审题析题，不应停留在问题的表面以及问题成功破解的第一步，而是不断进行认真研究，解后思考、探究、拓展、变式、总结等，深入进行“一题多解”“一题多思”“一题多探”“一题多变”“多题一解”等创新应用，归纳总结题目类型与破解规律，不断发展学生的机智和创造力，全面提升综合能力、创新能力与应用能力等．