从教材立意,走向深度学习
——挖掘导数概念的立意
江苏省淮阴中学 胡桂东 陈伏香
江苏省清浦中学 吴洪生
立足于教材立意,对教师认识理解数学具有启发意义,才能充分发挥教材对数学教育的功能.在暴露思维的解题活动中,为让复杂问题简单、形象、生动,提升学生探究问题的能力,从而走向深度学习,教师要对教材进行精心创作,在帮助学生对数学概念的理解过程中为学生的深度学习提供广阔的空间.
1 高中导数课程与教学现状概述
高中“导数”内容是建立在必修一“函数”基础之上的选修课程.用高等代数的方法研究函数问题,是对初等函数问题研究的延续、内容的扩充、方法的提升、思想的引领,是研究与完善函数问题的关键之举.教材的立意格局是开阔和深邃的,教师应当从中可寻找到:是什么?为什么?怎么做?换言之,将“知识背景、章节理念、过程实践、文化诠释、主线梳理”等环节都贯穿于教材立意之中.
新课标教材中“导数”这一章的内容在高中数学中的地位格外重要,函数图象的切线成为命题的热点,也是高中数学教学的难点.但是,“导数”课程教学的“尴尬”之处在于教师在教学这程中普遍重视刷题,用教辅资料取代教材,忽视教材立意与格局,违反教学规律,学生没有知识基础:(1)没有学过极限直接学导数,本身给导数教学带来的是一种不清不楚的知识环境;(2)高中数学对切线的概念并没有详细的说明(仅在《选修2-2》中有描述性介绍);(3)导数中很多结论直接给出并要求学生学会运用,学生掌握的知识很脆弱.所以教学中绝大部分学生是“食之无肉,去之无味”,在综合题中表现为理解能力不足,忽视教材教学导向功能,应当改变目前高中教材使用现状,深入理解、领悟教材立意,正确认识教材的教学价值导向,笔者根据选修教材“导数”中对导数概念的理解,结合案例谈谈教材的立意.
2 教材的立意探索
2.1 建立理解目标
在课堂教学实践中,教师为了凸显教学内容的重难点,往往以简单的记忆、训练来代替对数学问题的理解,一味地把教学的重心指向所谓的学习内容的知识“核心”,学生在观察、思考过程中,因为思维没有深度参与,形成对所学数学知识概念的“概念表象”,阻碍了学生向学习目标深处追溯的意愿,降低了教学目标的达成度,使得“高效课堂”的背后埋藏着未被学生掌握的“核心知识”.
美国数学家哈尔莫斯提出过“问题是数学的心脏”的精辟论述,要聚焦解决什么问题,才能建立理解目标.在教材“导数”章引言的案例中,气温“陡增”的数学意义是什么?用怎样的数学模型刻画变量的快与慢?所以,如何建立平均变化率模型就是引领学生深度思考,探究问题本质的关键;建立平均变化率的模型,就是建立导数概念的理解目标.
2.2 建构理解系统
无论是立于一章的设计,还是立于一节课的设计,都应当考虑教学内容和学生整体思维的过程,在知识构建、探究策略、反思总结、拓展升华等方面建构理解系统.通过问题情境—问题提出—问题解决—学生活动(建立数学—运用数学—反思升华)这个过程提炼、建构理解系统,能够让学生全面掌握章节核心知识,这也是教学设计的主线.如何建构?可以结合教材的章引言、教材每节的标题、章节回顾、文化阅读提炼关键的线索.建构导数概念的设计,如图1所示.
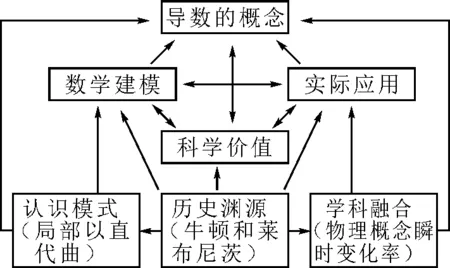
图1
2.3 明确理解主体
现代数学学习理论认为:数学学习是一个数学认知的过程.因此,要对数学知识形成过程中的内部认知加以分析,数学思想的学习要经历感性到理性、从领会到形成、从巩固到应用的发展过程.如何让学生理解导数的概念便是该章节学习的关键,教材中对“陡峭程度”是这样描述的:平均变化率是曲线陡峭程度的“数量化”,或者说,曲线陡峭程度是平均变化率的“可视化”,前者是“数”的表达,后者是“形”的立意.
数形结合思想学习的心理建构过程需要经历以下4个阶段:
(1)辨认:通过初中的已知物理概念“平均变化率”的相关知识,确认数形结合思想内在统一的两个方面.
(2)分化:从函数曲线“增与减”的直观代数化和“平均变化”到“瞬时变化”的几何化对心理产生不同的刺激反应.
(3)交互:几何问题代数化和代数问题几何化以彼此对立的方式在心理上运行.
(4)内化:数形结合思想,以一种综合的心理图式转化为内部观念.
课堂实践要以学生为教学主体.教师要引导学生在探索与创造的过程中培养认识、搜索与整理信息的能力,不能将自己的主观经验直接灌输给学生,知识传播要符合学生的认知规律,要建构对理解的目标设计.因此教师必须足够重视教材对概念的引导和启发.
2.4 发掘理解项目
奥苏伯尔认为:学生的认知起点是学生学习是否成功的前提.教师在帮助学生对问题进行深入学习时,应着眼于学生思维的发展.在解决问题的过程中完成对数学学习的认识、对项目的理解,应注重学生认知的起点,重视认知过程的层次性;同时,在解决问题的过程中,使其自身不断产生新的问题,促进学生对原来问题进一步的认识,随着新问题的提出使其自身思维进一步发展.

图2
教材中,利用割线逼近切线的方法,通过图示的动态模拟方式建构导数概念的初步感性认识,挖掘导数概念的内涵进行深度学习.结合教材图示(如图2),尝试解读.
2.4.1 割线斜率的动态变化与切线静态斜率之间建立的等量与不等量关系的内涵


图3
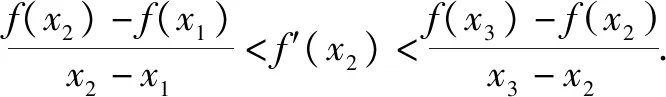
2.4.2 割线斜率的动态变化揭示直线与静态函数曲线之间位置的内在联系
例2设k,b∈R,若不等式kx+b≥lnx对任意实数x∈(0,+∞)恒成立,求k+b的最小值.

图4
思路点拨:如图4,不难想到将条件中不等式左边看成不等式右边函数图象的切线.


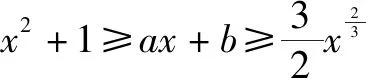

图5
思路点拨:过点(0,b)分别作f(x),g(x)的切线,使直线y=kx+b在两切线之间.如图5.


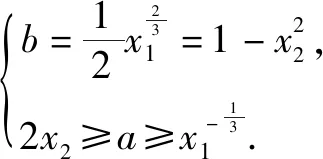

例4已知函数f(x)=(x+1)lnx-ax+a(a为正实数,且为常数).若不等式(x-1)f(x)≥0恒成立,求实数a的取值范围.
思路点拨:不等式(x-1)f(x)≥0恒成立可等价于x≥1时,(x+1)lnx≥a(x-1)恒成立;0 简解:根据数形结合法可求出实数a的取值范围(0,2]. 通过几个案例分析,了解了切线与函数图象的位置关系,题目的立意几乎都源自导数的概念.数学解题是一种思维活动,教师要摒弃繁杂套路的解题教学,回归教材关注数学问题的本质. 图6 将对教材的研究融入课堂实践,在概念教学中寻找新的生长点,立足于教材结合学生的认知规律,设计教学是学生走向深度学习的前提,也是问题设计的思想源泉.挖掘教材内涵,发挥教材教学功能,让教学回归良性的教育生态.2.5 梳理理解成果



