复杂网络能控性鲁棒性研究进展

楼洋 李均利 李升 邓浩

复杂网络作为现今科学研究中的一个热点学科,在过去20 年里得到了巨大的发展[1−4].复杂网络普遍存在,如互联网、神经网络、交通运输网[5]等.同时许多系统,如人际社会关系[6]、学术合作[7]、人类迁徙[8]等都可以抽象为复杂网络,以进行系统地分析和研究.除了广泛应用于数学、工程、经济等学科之外,复杂网络更与我们的日常生活息息相关,如在信息的传播[9]、语言的演变[6,10−12]、流行病的传播和阻断[13−15]、网络群体智能[16−17]等方面,复杂网络都提供了极有价值的参考模型和分析工具.

复杂网络能控性(Controllability)是复杂网络研究的一个核心问题[18−33],其概念是指在有限时间内,通过适当的控制输入,控制网络从任意初始状态到达一个目标状态的能力.人类对自然系统和技术系统的理解,最终体现在如何有效地控制它们,使之为人类的生存和发展服务.作为一个跨学科的研究领域,网络科学与控制系统理论之间的跨学科研究在过去20 年里得到迅速的发展.

由于复杂网络通常具有大量的节点和连边,其中高维动态节点系统相互连接,这给经典控制理论和技术带来了新的机遇,但同时也带来了巨大的挑战.对于复杂的动态网络,要达到最佳控制目标,往往只需要通过外部输入控制小部分节点或连边.作为实现网络优化控制的实用方法之一,牵引控制(Pinning control)策略[34]旨在通过高效的算法来回答 “牵引控制多少节点和哪些节点” 的问题,以最少的能量消耗和代价,达到牵一发而动全身的最优效果.

复杂网络在攻击下维持能控性的能力称为能控性鲁棒性(Controllability robustness).本文中 “攻击” 的表现形式为删除节点或连边.近年来,对复杂网络的攻击成为主要关注的问题之一[35−45].这些随机或恶意的攻击可能导致系统瘫痪等严重后果.复杂网络的能控性理论为研究神经网络结构和功能之间的联系提供了分析工具,如分析秀丽线虫(Caenorhabditis elegans) 的各神经元功能及其与肌肉运动的联系[46].而能控性鲁棒性则为进一步研究提供分析基础,如秀丽线虫部分神经元损坏可导致生物功能障碍和疾病[46],这里神经元损伤可看作网络拓扑结构受到攻击,即网络中的节点和连边受到破坏和攻击.此外,能控性鲁棒性的研究对交通运输、电力、社交网络的鲁棒控制具有重要的指导意义.

在不同背景下,复杂网络抵御攻击的能力 (或称 “抗毁性”) 具有不同的定义和度量[47].在维持连通性能力(Connectedness)[37, 45,47−48]的研究中,抗毁性是指复杂网络在攻击情况下保持连通性的能力.在能控性研究中,抗毁性是指网络维持能控性的能力.为避免混淆,本文将保持连通的抗毁性称为 “连通鲁棒性”;将保持能控性的抗毁性称为 “能控性鲁棒性”,也是本文的主要讨论对象.良好的能控性以较强的连通性为基础,但是,强的连通性却不能保证良好的能控性.同样地,良好的能控性鲁棒性以良好的连通鲁棒性为基础,而良好的连通鲁棒性并不能保证良好的能控性鲁棒性.能控性鲁棒性较好的网络系统具有好的抵御攻击的能力,同时能延迟系统的整体瘫痪,为攻击后的补救争取时间.相反地,能控性鲁棒性差的系统则容易在受到攻击以后,迅速导致网络系统的整体失效.因此,实用的控制网络模型应同时兼备良好的能控性和能控性鲁棒性.基于当前理论研究的局限和日益发展的超级计算能力,复杂网络的能控性鲁棒性研究以仿真实验研究为主[49−50].同时,深度学习的发展也为这一领域提供新的研究技术[51−53].不同类型网络系统具有不同的能控性计算方式,如有向和无向网络,无权和有权网络,以及单输入单输出和多输入多输出系统等,因而其能控性鲁棒性的研究与优化也有所不同.本文主要阐述针对有向网络的能控性鲁棒性研究,主要关注以下3 个关键问题:

1) 如何定义和度量复杂网络的能控性鲁棒性?能控性鲁棒性的定义和度量为不同拓扑结构的优劣提供比较标准,为不同攻击方式的破坏能力提供参考,也为复杂网络的优化提供依据.不同的定义方式具有不同的理论依据及其侧重点,导致不同的比较结果.在计算方式上,基于仿真的能控性鲁棒性的计算得到的结果真实准确,但需要较大的计算量,而基于深度神经网络的能控性鲁棒性预测则可以较小的计算代价取得相对准确的估值.

2) 常见的攻击方式有哪些? 哪些攻击对能控性的危害最大? 针对不同的攻击方式,复杂网络可能表现出不同的能控性鲁棒性,所以研究攻击方式对于复杂网络的能控性鲁棒性有重要意义.通过分析常见的攻击方式及其危害程度,可以理解网络中节点、连边和其他特征对能控性鲁棒性的重要程度;找到危害最大的攻击对于评价网络的性能也有着重要的意义,启发式攻击由计算智能算法自主选择攻击对象,可以达到相较于传统方法更大的破坏效果.同时,对网络攻击的研究也有助于对网络优化的研究,对网络的攻击的理解和将其应用于优化犹如理解 “矛与盾” 的关系,既相互抑制,又相互促进.

3) 怎样提高能控性鲁棒性? 如何达到最优的能控性鲁棒性? 对复杂网络的能控性鲁棒性优化问题属于NP (Nondeterministic polynomial time)难问题.但是由于能控性鲁棒性度量方式,攻击方式,以及限制条件等的不同,使其成为一个多目标优化问题.同时,由于基于仿真的能控性鲁棒性度量普遍耗时较多,以及节点和连边特征与能控性鲁棒性之间相关性不够明确等问题,给该优化问题带来了挑战.

围绕以上3 个问题,本文就能控性鲁棒性研究现状与进展进行归纳总结,指出当前研究中存在的问题与技术挑战,并探讨了未来发展趋势.

1 复杂网络的能控性鲁棒性

1.1 预备知识

1.1.1 无权有向网络

对于一个无权有向网络G=(V,E),其中,V={1,2,···,N}和E={Aij|i,j∈V}分别为节点和连边集合.邻接矩阵A中元素Aij定义为

其各节点的出度和入度可由邻接矩阵计算,即

各节点的介数可由式(3)计算,即

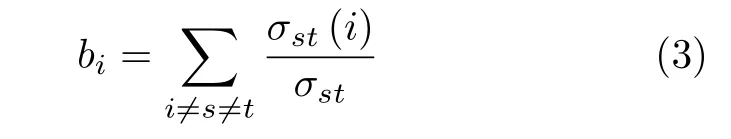
其中,σst是从节点s到节点t的所有最短路径总数,σst(i) 表示这些路径经过节点i的次数.对于有向网络,如果从节点s到t存在最短路径,则称节点s到t可达,否则称为不可达.

1.1.2 复杂网络能控性

复杂网络能控性的概念由卡尔曼[54]在1960 年首先提出.对于一个复杂网络系统或线性时不变(Linear time invariant,LTI)系统

其中,A和B分别为N ×N和N ×ND常系数矩阵,分别代表网络的邻接矩阵和LTI 系统外部控制器所控制的节点,x是状态向量,u是控制输入,卡尔曼准则 (Kalman criterion)[54]提出该系统能控的充分必要条件是系统的能控性矩阵

满足行满秩,该能控性称为复杂网络的状态能控性(State controllable).结构能控性的概念是状态能控性的泛化.对于常参数系数矩阵A和B,如果存在一组非零参数值可以确保系统是状态能控的,那么则称该系统是结构能控的(Structural controllable).对于一个能控系统,其状态向量x可以通过适当的控制输入u(ND×1 向量),从任意初始状态驱动至任意目标状态.

1.1.3 匹配

匹配(Matching)是指由连边所组成的集合,该集合中的任意两条连边不共享起始节点和终止节点.连边集合E中除了匹配连边,其余均为非匹配.最大匹配(Maximum matching)包含了最大可能的匹配数目.最大匹配并不唯一.如果一个节点是一条匹配连边的终止节点,则该节点是匹配节点(Matched node),否则是非匹配节点.在完全匹配(Perfect matching)中,所有的网络节点均为匹配节点.图1(a)链式网络的最大匹配包含3 条连边,除了起始节点1之外都是匹配节点;图1(b)所示4 节点星型网络的最大匹配包含1 条连边,且不唯一(3种情况);图1(c)网络的最大匹配包含5 条连边,且不唯一(最大匹配可包含连边(5,6)或(5,7)).其类仙人掌型结构具有较好的能控性[55].

图1 匹配和节点控制中心性的例子Fig.1 Examples of matching and node control centrality

1.1.4 节点控制中心性

节点控制中心性(Control centrality)[38]度量单个节点做为控制节点的控制范围,其定义为

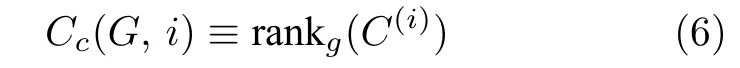
其中,Cc(G,i) 表示复杂网络G中节点i的节点控制中心性,C表示网络能控性矩阵(Controllability matrix),可由式(5)计算; r ankg(C(i)) 表示能控子空间的一般维度,可根据Hosoe 理论[56]计算.控制中心性大的节点能控制的范围较大,适合作为控制节点.图1 中阴影部分表示每个网络中节点1 的能控子空间.图1 给出了节点控制中心性的相关例子: 图1(a)中节点1 的控制中心性为4;图1(b)中节点1 在3种情况下的控制中心性都为2;图1(c)中节点1 的控制中心性为6.

1.1.5 关键连边和关键节点

Liu等[18]将有向网络连边依据其对能控性的贡献分为3 类: 1)关键连边,删除任一关键连边会导致系统能控性下降,也就是需要额外增加一个控制节点;2)冗余连边,删除任一冗余连边不影响系统的能控性;3)普通连边,删除一条普通连边不会导致能控性下降,但是会改变可能的最大匹配.其中冗余连边和普通连边可称为非关键连边.图2(a)和图2(c)分别举例说明了关键连边与普通连边.

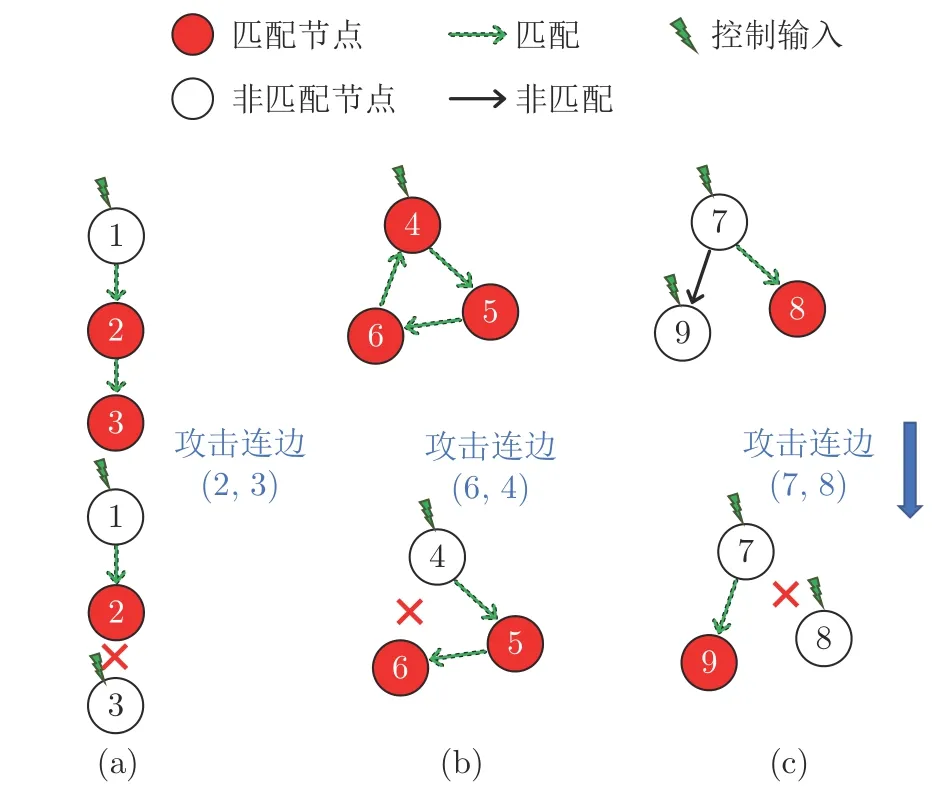
图2 按文献[57]连边分类举例Fig.2 An example of edge classification according to [57]

Lou等[57]依据其对结构能控性(见式(8))鲁棒性的贡献,将所有连边分为3 类: 1) 关键连边,定义与文献[18]相同;2) 亚关键(Subcritical)连边,遭攻击后不会改变控制节点数,但是会增加1 个非匹配节点;3) 普通连边,被攻击后既不会影响控制节点数,也不会增加非匹配节点数.注意文献[57]定义的 “普通” 连边包含了文献[18]定义的 “普通”和“冗余” 连边.

图2 分别给出了关键连边(图2(a))、亚关键连边(图2(b))和普通连边(图2(c))的例子.同时,文献[57]将该分类扩展到节点,将所有节点分为4 类:1)关键节点,其遭攻击后须额外增加1 个控制节点;2)亚关键节点,遭受攻击后不影响控制节点数,但会使非匹配节点增加1;3)普通节点,其遭攻击既不影响控制节点数,也不影响非匹配节点数;4)冗余节点,其遭受攻击后使得所需控制节点数下降1,冗余节点是从能控性角度的 “孤立节点” (不一定与其他节点没有连边).

图3 给出了节点分类举例.图3(a)中节点2 是关键节点,遭攻击后节点1和3 分别须单独的控制输入;图3(b)中节点6 是亚关键节点,遭攻击后虽然控制节点数不变,但节点4 由匹配节点变为非匹配节点;图3(c)中节点7 为普通节点,遭攻击后控制节点数不变,非匹配节点数也不变(原先非匹配节点为7和9,攻击后非匹配节点为8和9);图3(d)中节点8 为冗余节点,将其删除后,系统所需控制节点减少1.

图3 按文献[57]节点分类举例Fig.3 An example of node classification according to [57]

1.2 能控性度量

通常,复杂网络能控性可由控制节点的密度(nD)来量化表示,即

其中,ND是系统所需控制节点的总和,N是系统中节点数总和.nD∈[1/N,1],当nD=1/N表示当前网络的N节点只需一个控制节点,此时的能控性最佳;而当nD=1 则表示当前网络的每个节点都需要一个单独的控制器,此时网络能控性最差.系统具有较小的nD值,表示该系统的能控性较好.

常用的控制节点数ND计算方法有两种,分别根据结构能控性[18]和精确能控性(Exact controllability)[20].结构能控性可由匹配(Matching)计算,依据最小输入理论(Minimum inputs theorem)[18],控制节点数可由最大匹配计算得到,即

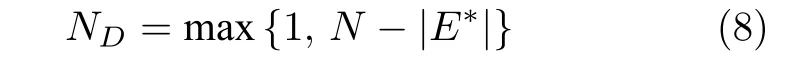
其中,|E∗|是最大匹配E∗中的连边数.式(8)说明网络所需控制节点数等于网络中非匹配节点的个数.当网络非完全匹配时,需ND=N −|E∗|个控制节点,即将控制器加载于ND个非匹配节点.当网络为完全匹配时,仅需ND=1 个控制节点,此时控制器可加载于任意节点.

为了识别任意结构以及加权网络达到能控状态所需的最小驱动节点数,Yuan等[20]根据卡尔曼准则的等价条件PBH (Popov-Belevitch-Hautus) 秩提出精确能控性,其所需控制节点个数可由式(9)计算获得,即

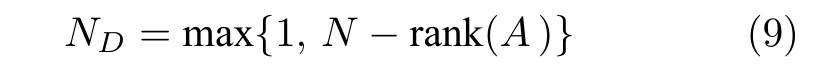
如果矩阵A满秩,需ND=1 个控制节点;否则,需N −rank(A)个控制节点.

1.3 能控性鲁棒性定义

复杂网络能控性描述了当前系统的能控性状态;而能控性鲁棒性则刻画在受到攻击的情况下,复杂网络能控性的变化情况.

常用的能控性鲁棒性定义包括基于能控性曲线的定义,基于节点控制中心性的定义,以及基于排序的定义.其中基于能控性曲线的定义参照常用的连通鲁棒性定义.常用的连通鲁棒性度量基于最大连通子图LCC (Largest connected component)[37],在节点攻击情况下,其计算为

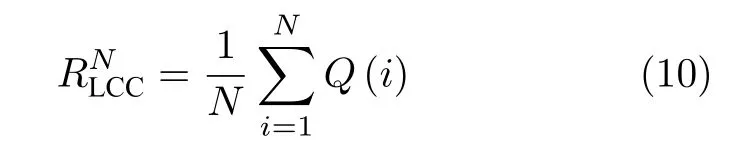
其中,Q(i) 表示当网络中i个节点被攻击之后,最大连通子图的节点数占当前网络节点总数的比例,其范围是 [ 1/N,1],当Q(i)=1/N表示该网络包含N个离散节点,而当Q(i)=1 则表示该网络节点互相连通.类似地,RLCC在连边攻击时计算为

其中,Q(i) 表示当网络中i条连边被攻击之后,最大联通子图的节点数占当前网络节点总数的比例;M为网络中的连边总数.式(10)～(15)中的上标N和E分别表示节点攻击和连边攻击.

1.3.1 基于能控性曲线的定义

能控性鲁棒性即系统在遭受节点或连边攻击之后,余下网络的能控性.它是一组能控性值的序列,其中节点攻击下能控性鲁棒性定义为

其中,ND(i) 是当i个节点遭受攻击后,所需的控制节点数;N −i为i个节点遭攻击后的网络剩余节点数,随着每次攻击逐一减少.同样地,连边攻击下能控性鲁棒性定义为

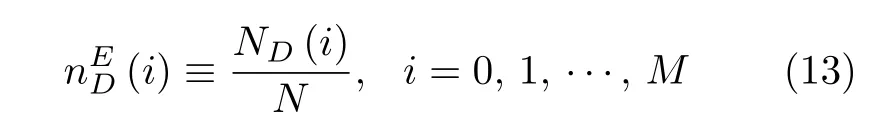
其中,ND(i) 是当i条连边遭受攻击后,所需的控制节点数;N和M分别表示网络节点和连边数.注意在连边攻击下节点数不变,而连边数逐一减少.当表示遭受攻击前的初始网络能控性.

式(12)和式(13)定义了攻击情况下能控性变化的动态过程.而整体的能控性鲁棒性可由平均得到,如式(14)和式(15)所示.

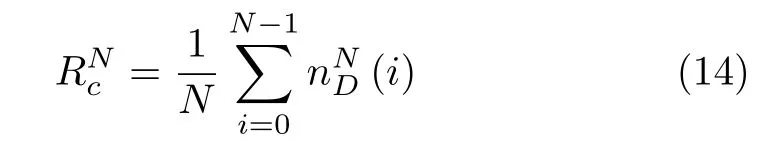
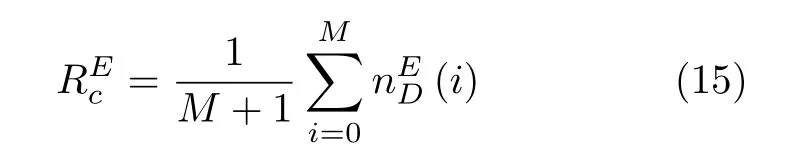
其中,较小的或值分别表示在节点或连边攻击的情况下,具备较好的整体能控性鲁棒性.该度量方式与常用的连通性鲁棒性的度量LCC[37]类似.式(14)与式(10) 区别在于: 1) 函数(·)和Q(·)的物理意义和计算方式不同;2)考虑到各网络的初始能控性(0) 不同,因而须从i=0 开始累加,而一般情况下,网络的初始状态均连通,即Q(0)=1,因而可忽略.

1.3.2 基于节点控制中心性的定义

Usman等[58]将能控性鲁棒性定义为节点和连边受攻击以后能控子空间(Controllable subspace)的剩余维度,提出了预期鲁棒控制中心性ERCC(Expected robust control centrality).假设对复杂网络G中任意n个节点进行攻击,则节点i做为控制节点的预期鲁棒控制中心性可由如下计算得到,即

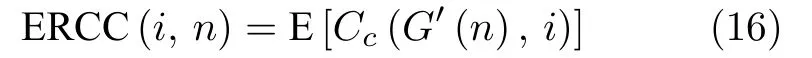
其中,G′(n)是由G删除n节点后得到的网络;Cc(G,i)表示网络G中节点i的节点控制中心性; E [·] 表示数学期望.作为预期鲁棒控制中心性的扩展,即

其中,e是节点i可达的任意一条边.相较于ERCC而言,GRCC (Generic robust control centrality)不限定在当前网络中攻击n个节点这一条件.ERCC和GRCC 适用于度量随机攻击情况下,某节点i的控制范围的鲁棒程度,因而可根据ERCC 或GRCC 选择适当的控制节点.

由于式(16)和式(17)计算量巨大,Usman等[58]提出了一种均匀采样的估值方式,降低了部分计算量.该鲁棒性度量适合于评估选择哪些节点适于作为鲁棒的控制节点.

1.3.3 基于排序的能控性鲁棒性度量

Chen等[50]提出一种基于排序比较的能控性鲁棒性度量.该度量计算在相同的受攻击程度下(受攻击的节点或连边比例相同),不同网络的能控性(根据式(7)计算)的排序,依照排序确定能控性鲁棒性: 排序靠前的较好,排序靠后的较差.

图4 列举了两个复杂网络net1和net2 在受到同种攻击情况下的能控性曲线,其中Rc表示基于能控性曲线的能控性鲁棒性,Rk表示基于排序的能控性鲁棒性.对两个网络在相同的受攻击节点比例下进行比较排序,例如,当受攻击节点比例为0.1 时,net2 排序为1,net1 排序为2.Rk为其排序的整体平均值.

图4 能控性鲁棒性度量方式比较举例Fig.4 Comparison of two different controllability robustness measurements

从网络攻击的过程来看,net2 的初始能控性较好,而受到攻击时能控性下降 (所需控制节点密度上升) 速度较快,net1 的初始能控性较差,但是在攻击中维持较好.根据能控性曲线的平均值(Rc(net1)=0.72,Rc(net2)=0.69),net2 的能控性鲁棒性更好;而根据基于排序的度量(Rk(net1)=Rk(net2)=1.5),两者能控性鲁棒性等价.两种度量的侧重点不同,相对基于能控性曲线的定义,基于排序的度量更注重鲁棒性,而弱化了能控性本身和初始能控性的比重;其缺点在于该方法只能根据给定方法和结果比较,无法推广到的一般情况.基于上述理由,本文对能控性鲁棒性的讨论以第1.3.1 节的基于能控性曲线的定义为基准.

1.4 能控性鲁棒性的预测

对一个N节点M连边的复杂网络,其点攻击和边攻击次数范围分别为 [ 0,N −1]和[ 0,M],每次攻击以后以式(8)或式(9)计算网络的当前能控性,可得能控性曲线.以Hopcroft-Karp算法为例,计算式(8)的复杂度为[59];以Coppersmith-Winograd 算法为例,计算式(9)的复杂度为O(N2.37)[60].通过仿真获得的曲线精确但耗时.Sun等[61]提出了在随机和蓄意攻击下的能控性曲线近似预测.Lou等[52]通过训练卷积神经网络[62],获得能控性鲁棒性曲线的近似预测,其预测误差小于样本方差,同时将计算速度提升 1 02∼103倍[52].进一步地,文献[63−64]通过加入先验知识,提高了卷积神经网络的预测精度,同时比较得出该预测精度优于谱度量(Spectral measures)[65]和异质性(Heterogeneity)[66]等方法.值得一提的是,深度学习也应用于分析和预测其他非解析的网络属性[53,67].

1.5 能控性鲁棒性研究框架

目前的研究成果主要集中在对复杂网络的拓扑结构的探索和优化两个方面.

对拓扑结构的探索体现在研究复杂网络中节点和连边对维持能控性鲁棒性的重要性,即寻找网络中的关键节点和连边.由于目前尚没有可以预测能控性鲁棒性优劣的可靠详实的理论依据,而且经验指标也不充足,这一研究目标主要依靠设计高效的攻击策略来实现.本文第2 节回溯了随机攻击、基于特征的蓄意攻击和启发式攻击,其中基于特征的蓄意攻击和启发式攻击的研究对探索预测能控性鲁棒性优劣的指标 (或经验指标) 具有重要意义.

对拓扑结构的优化主要包括模型优化设计和重新连边.本文第3 节回顾了主要的优化策略,同时介绍了全齐性和模体 (包括环和链等) 结构对提高能控性鲁棒性的重要意义.

2 针对能控性鲁棒性的攻击

能控性鲁棒性体现了在攻击下,系统保持能控状态的优劣.在不同攻击方式下,不同的复杂网络系统呈现出不同的鲁棒性.攻击的类别基于对象可分为节点攻击和连边攻击.通常,对节点攻击后,该节点及其所有连边从当前网络中删除;对连边攻击后,仅该连边从当前网络中删除.

按攻击目标的不同可分为随机攻击和蓄意攻击.随机攻击指无差别地破坏、删除复杂网络中的节点或连边;蓄意攻击则优先攻击被认为最重要的节点或连边,例如度数最高的节点.同时,不同的攻击方式针对不同的复杂网络功能,如图5 所示,一种对网络连通性的破坏较大的攻击,对于能控性的破坏未必较大.图5(a) 中的星型网络,其所需控制节点数为4,其最大连通子图LCC[37]为6 (即 6 个节点之间均有连边相连);当中心节点被攻击后,其所需控制节点数为5 (增加25%),而其最大连通子图降为1 (减少83%).

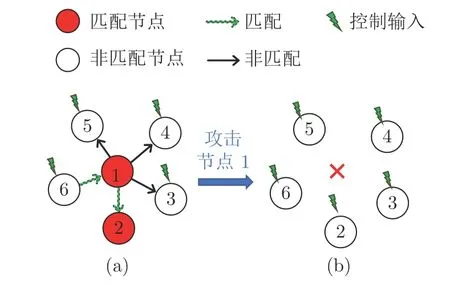
图5 能控性鲁棒性与连通性鲁棒性Fig.5 Controllability robustness and connectedness robustness

由于网络连通性和能控性既有一定的相关性又存在差别,即能控必须连通,而连通未必能控.本文讨论的攻击以破坏网络能控性为主,文中描述的攻击效果以破坏网络能控性为目标.

2.1 随机攻击

随机攻击是指均匀随机地选择复杂网络中的节点或连边进行攻击.Sun等[61]指出,在随机攻击下,网络所需控制节点数的增量,可以根据网络中关键连边的数量估算得到,即

当被攻击的连边数小于关键连边数时,关键连边会以p(Mc)=Mc/M的概率被攻击.每攻击一条关键连边,所需的控制节点数增加1;若攻击到非关键连边,所需控制节点数保持不变.如果被攻击的连边总数大于关键连边数(即Mr >Mc),则式(18)不成立,因为此时网络中的关键连边已经发生变化.实际上,攻击1 条连边就可能引起关键连边的变化,如图6 举例所示.在图6(a)中 连边(2,4)原本是非关键连边,当连边(2,3)和(3,4)被攻击以后,则变成了关键连边;在图6(b)中节点2,3,4原本都是关键节点,但当节点1 被攻击以后,它们都成为非关键节点;接着,当节点4 遭受攻击之后,节点2 又成为关键节点.

图6 关键连边和关键节点在遭受攻击过程中变化Fig.6 Critical edges and nodes may change during attacks

Liu等[38]利用有向网络中的层级结构,设计了随机上/下游攻击,旨在攻击随机选取的节点的上游或者下游节点.该攻击比普通随机攻击以更大的概率攻击到枢纽(Hub)节点,因而比普通随机攻击更有效.以图1(c)中节点5 为例,其上游节点为节点1,下游节点为节点6和7.

2.2 基于特征的蓄意攻击

区别于随机攻击,蓄意攻击的攻击者选取主观认为的最有效对象进行攻击,因此,蓄意攻击的效果一般比随机攻击更显著.通常假设攻击者具有对被攻击网络的必要知识,如最大度数节点、最大介数连边等,并且该知识能在攻击后得到更新.常用于破坏复杂网络连通性的攻击特征包括度数和介数,以及邻里相似度(Neighborhood similarity)[68]、分支权重(Branch weighting)[69]、结构孔(Structural holes)[70]等.通常,攻击者主观地认为该知识(网络特征)能带来最优的破坏效果,然而,度量复杂网络节点和连边在维持能控性方面的重要性,是一个复杂而艰巨的任务,尤其是对较大规模网络.绝大部分基于单一特征的攻击并不能给网络带来持续的、最有效的破坏.

网络拓扑结构与能控性之间关联的研究较多[27,32,71−73],而与能控性鲁棒性相关的指标或特征研究相对较少.目前尚无可以预测能控性鲁棒性优劣的可靠详实的理论依据,而且经验指标也不充足.节点攻击的研究较多,而连边攻击的研究较少[74],其原因是: 1) 节点攻击相对有效,攻击节点时其连边也同时被删除,而连边攻击并不影响节点;2) 节点的特征属性相对明确,而连边的属性相对模糊,如有向图的节点具有明确的出度和入度定义,而连边的出度和入度不同定义较多[35,47,75].

2.2.1 基于度数和介数的攻击

基于度数的攻击旨在攻击网络中度数最大的节点(或连边).Holme等[35]将基于度和介数的节点攻击分别分为基于初始分布的攻击和重新计算分布的攻击.前者依据最初网络的度数或介数分布,由大到小依次攻击,而后者则在每次攻击后重新计算.由于网络的统计特征在攻击后通常会发生较大变化,重新计算的攻击效果要优于基于初始分布的攻击[35,76],因而本文默认基于度数或介数的攻击中,度数或介数最大的节点需要在每次攻击后重新计算.

基于度数和介数的攻击既是破坏网络连通性的最常见攻击方式,也是破坏能控性的常用方式.基于度数的攻击是局部策略,其重点是尽可能快地减少总连边;而基于介数攻击是全局策略,专注于尽可能多地破坏全局最短路径.基于度数和介数的节点攻击分别定义为

Nguyen等[77]观察发现基于介数攻击在攻击后期效果变弱,由此设计了一个约束条件,即如果当前(全局)介数最高节点属于最大连通子图,则攻击该节点;否则攻击最大连通子图(局部)介数最大的节点.

作为最常用的攻击度量,度数和介数经常一起用于攻击.Nie等[76]通过预先给度数最大和介数最大的节点分配权值来分配两者被攻击的概率,即

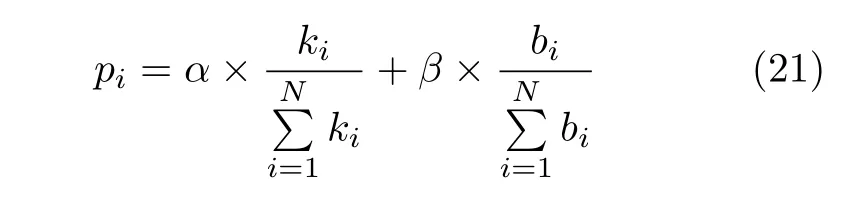
其中,ki和bi分别为节点i的度数和介数,pi是攻击该节点的概率,α和β为预先设定的权值.Gao等[78]将式(21)中的β替换为 1−α.进一步地,Hao等[79]设定了3 个参数α,β和γ来控制度数、介数和谐波接近度(Harmonic closeness)在攻击中的权重.这些攻击策略应用于互依网络(Interdependent networks)[78−82]、网络的网络(Networks of networks)[83−84]以及加权网络(Weighted networks)[85]等.

研究发现,基于度数的节点攻击[86]比随机节点攻击更能有效地破坏随机网络和无标度网络的能控性.Lu等[87]发现节点攻击的破坏力大于连边攻击,同时,异质网络的能控性鲁棒性要劣于同质网络.此外,对于许多实际网络来说,基于介数攻击对能控性破坏力最强[87].

对于本地世界网络(Local-world network)[88−89],Sun等[90]发现基于度数的节点攻击对本地世界规模较大的网络更具破坏力,而对本地世界规模小的网络破坏力较小.文献[90]的研究包括连通鲁棒性和能控性鲁棒性.Lou等[57]以最大度数和最大介数为依据,每次选取破坏程度较大的对象进行攻击.基于负载(介数)的连边攻击[91]能有效地破坏网络能控性.连边攻击不仅能破坏连通性和能控性,也能引起无标度网络的级联故障.

2.2.2 其他蓄意攻击

Wang等[92]提出的基于破坏力的攻击(Damage-based attack)以破坏程度作为选择攻击的度量,即攻击带来破坏程度最大的节点.这里的破坏程度以攻击前后LCC 大小的变化来度量.Lou等[57]提出在每次攻击中找到度数和介数最大的节点,选择带来破坏力较大的节点作为攻击对象,该方法对能控性的破坏力接近于基于度数攻击和基于介数攻击的破坏力上限.这类基于破坏程度的攻击要求攻击者具备比其他攻击更多的对攻击对象的知识.

基于模块的攻击(Module-based attack) 策略[93−94]旨在攻击具有多社区(Community)结构的网络中连接各社区的公共连边(Inter-community edge),从而达到破坏整体性能的效果.Ma等[95]让攻击与防御交替进行,并以此优化网络结构.

Sun等[61]提出了基于关键连边的攻击策略.该策略首选搜集网络中的所有关键连边,将其存储于列表并优先攻击,待列表中的关键连边全部攻击后,采用随机攻击策略.如图6(a)所示,一条关键连边在一次攻击之后就可能转换成非关键连边.Lou等[57]在文献[61]的基础上,提出了层级攻击(Hierarchical attack): 层级连边攻击依次删除网络中的关键连边、亚关键连边和普通连边.类似地,层级节点攻击依次删除网络中的关键节点、亚关键节点、普通节点和冗余节点.关键连边和节点的定义及举例见第1.1.5 节.同时,连边和节点的层级划分在每次攻击后得到更新.该方法计算复杂度较高但获得了有效的攻击效果.

2.3 启发式攻击

启发式算法(Heuristic algorithm)属于计算智能,是一种用于解决NP 难问题的有效方法,常见的算法包括模拟退火算法(Simulated annealing)、遗传算法(Genetic algorithm)、禁忌搜索(Tabu search)、粒子群算法(Particle swarm optimization)等.

前述的随机攻击和蓄意攻击通过预设的策略逐个选取攻击节点或连边;而启发式攻击则将整个攻击过程视作一个优化问题,通过启发式算法搜索最优攻击序列(即破坏效果最佳的攻击序列).对于一个N节点网络,其攻击序列的解空间大小为N!;对于一个M节点网络,其攻击序列的解空间大小为M!. 常用的编码方式为自然序号,即预先按1到N(或M)分别标记每个节点(或连边),通过选用适当的优化目标函数以达到优化攻击序列的效果.Zhang等[96]采用遗传算法,以连边的自然序号作为遗传编码,设计了可剔除重复基因的交叉和遗传算子,这里 “重复基因” 表示在同一个攻击序列中存在多个位置指向同一节点或连边.孙昱等[97]使用禁忌搜索最优攻击序列,通过局部交换,生成新的攻击序列,如果该序列在禁忌列表中 (在一定时间范围内生成且已经评价的相同攻击序列),则放弃该序列.该算法的计算成本高,适用于较小规模网络.Ventresca[98]利用启发式算法搜索网络中的关键节点.Deng等[99]通过禁忌搜索关键节点集合,提高网络解体的攻击效果,该方法计算成本较高.Qi等[100]以禁忌搜索提高多层网络的分解效果.Lozano等[101]以网络中最大介数为目标函数,通过人工蜂群算法(Artificial bee colony)来最小化这一目标函数,从而优化攻击效果.Li等[102]以邻域信息增强随机算法搜索关键节点集合的能力,显著提高攻击效率.

2.4 不同攻击下的能控性鲁棒性

本小节和第3.2 节可视为同一问题的不同角度分析.对于同一种网络在不同攻击下,使其能控性下降最快速明显的攻击为最有效攻击;将同一种攻击方式用于不同拓扑结构,其中能控性保持最好的网络可视为能控性鲁棒性最好的拓扑结构.

图7 给出了常见的9种网络模型在基于介数和度数的连边和节点攻击下的能控性曲线变化,包括随机图网络RG (Random graph)[103],小世界网络SW (Small-world)[104−105],随机三角形网络RTN(Random triangle network)[50,106],随机四边形网络RRN (Random rectangular network)[50],无标度网络SF (Scale-free)[107−108],洋葱型网络OLN (Onionlike network)[109−112],q-回路网络QSN (q-snapback network)[113−114],q-回路及反向连边QSNR (QSN with re-directed edges)模型[115],以及极同质EH(Extremely homogeneous) 网络[116].图中pE=Mr/M和pN=Nr/N分别表示已被攻击的连边和节点的比例.网络规模为节点数N=1 000,连边数M=5 000,所有数据来自20 次攻击的平均结果.

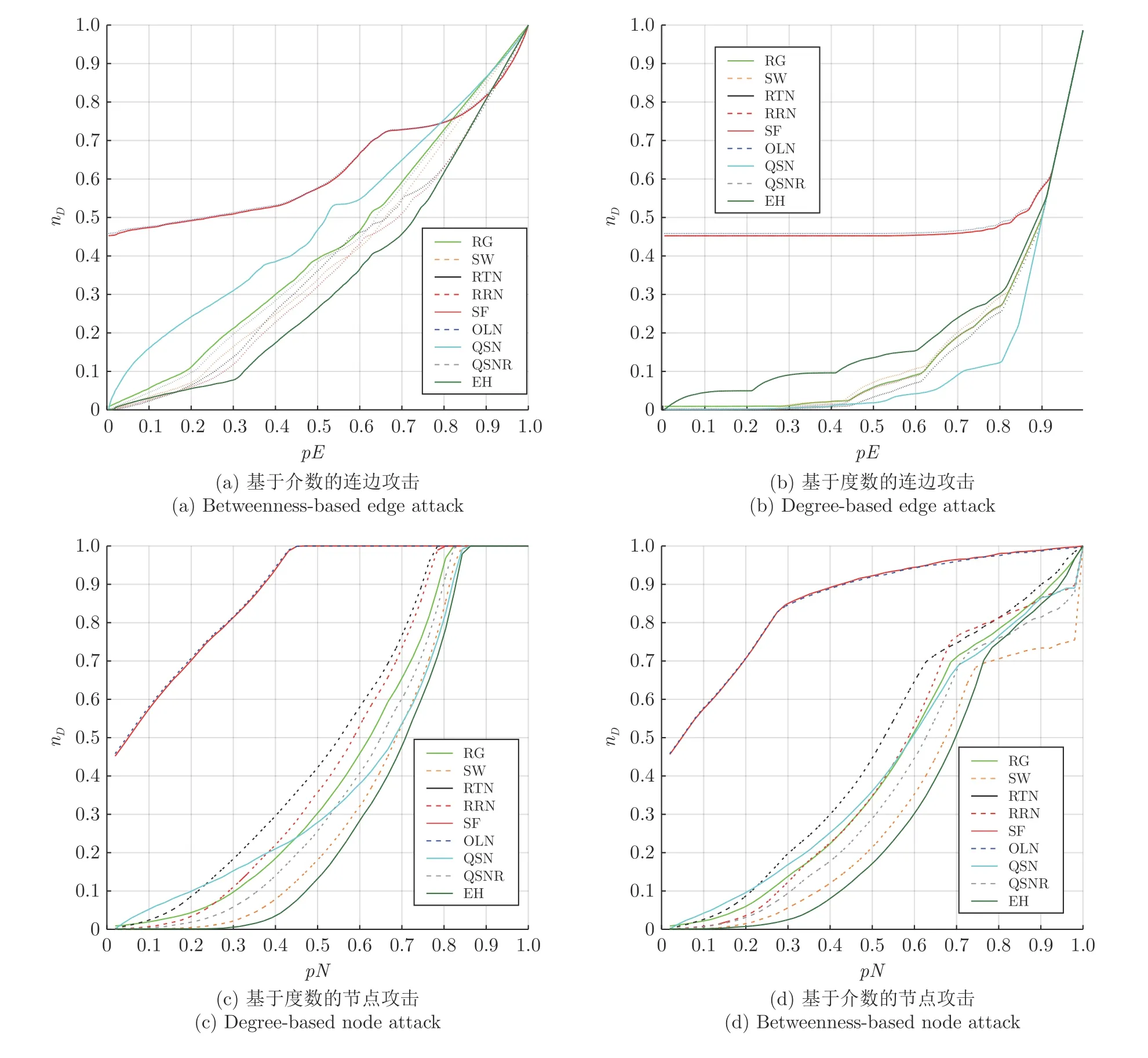
图7 常见的网络模型在攻击下的能控性曲线变化Fig.7 The controllability curves of 9 network topologies under 4 different attack strategies

由图可见,极同质EH 网络在图7(a)基于介数的连边攻击、图7(c)基于度数的节点攻击和图7(d)基于介数的节点攻击过程中,始终保持所需控制节点比例较低,相较于其他网络,EH 具有最佳能控性鲁棒性;而在图7(b)基于度数的连边攻击中表现较差.而无标度SF 网络和洋葱型OLN 网络则具有相似的能控性曲线,两者均为能控性鲁棒性最差的网络结构.在不同攻击下,各网络表现出不同的能控性鲁棒性,如QSN 在图7(a)基于介数攻击下的能控性只优于SF和OLN,而劣于其他网络;但在基于度数的连边攻击下,QSN 表现出最好的能控性鲁棒性,尤其在攻击的中后期.值得一提的是,使用不同的连边度数定义也会影响比较结果.

3 能控性鲁棒性优化

能控性鲁棒性优化旨在提高复杂网络对各种攻击的抵御能力.以第1.3.1 节的度量为例,定义如下.

定义 1.一个复杂网络G∗称为能控性鲁棒性最优网络(简称最优网络),当且仅当

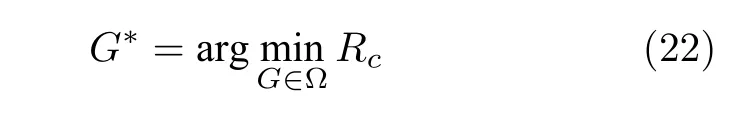
成立,其中,Ω 为适用解空间,即所有满足约束条件的复杂网络G构成的解空间;Rc可由式(14)或式(15)计算得到.

由于能控性鲁棒性优化属NP 难问题,而进化算法(Evolutionary algorithm)[117−118]和群智能算法[119]等智能计算[120−121]方法本身的计算代价较小,其计算成本通常取决于待优化问题的评价.因而,智能计算方法常应用于这一优化问题.

网络模型优化设计和对网络进行重新连边为常用的能控性鲁棒性优化手段.全齐网络拓扑结构在研究中认为是具有最优的能控性鲁棒性.此外,复杂网络中模体对保持网络能控性鲁棒性具有一定的促进作用.表1 列举了常见优化策略的优点与不足.以下各小节针对这几个方面分别进行讨论.

表1 常用能控性鲁棒性优化策略的优点与不足Table 1 Pros and cons of the strategies for controllability robustness optimization

3.1 网络模型优化设计

Yan 等基于同余论(Congruence theory)构造了同余网络MCN (Multiplex congruence network)[122],其生成方式如下: 首先对所有N节点进行1 到N编号,如果两个节点i和j满足:

则存在一条连边Aij,其中r为j除以i得到的余数.相同余数的所有节点构成同于网络的一层.同余网络的每一层是无标度网络,属异质(Heterogeneous)网络,其出度分布服从

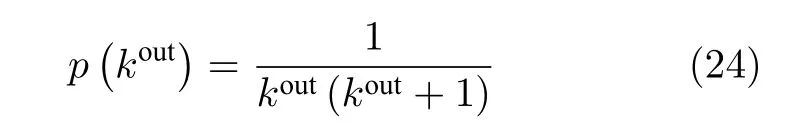
通常认为异质网络的能控性和能控性鲁棒性都较差[18,50],而同质(Homogeneous)网络的能控性和能控性鲁棒性都较好[18,116].但是由于主链(r=1层)的存在,使得同余网络具有较好的能控性和能控性鲁棒性,同时揭示了度分布非影响能控性鲁棒性的唯一原因.

Lou等[113−114]发现多链和多环结构有助于提高能控性鲁棒性,提出了基于工业流水线的q-回路网络QSN,由一条主链和若干回路构成,回路的数量由参数q∈[0,1] 控制.其第r(r=1,···,N −1) 层第i(i=1,···,N) 节点的出度可由下式计算:

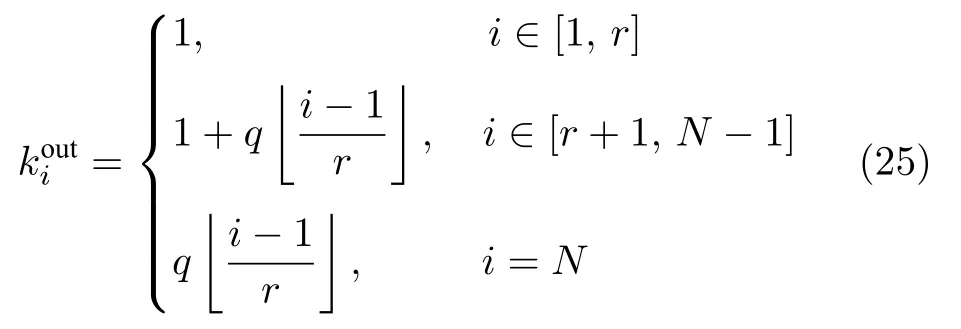
q-回路及反向连边QSNR 模型[115]基于QSN模型,同时加入随机反向连边,并保证主链不受影响.QSNR 的度分布服从泊松分布.虽然在不同攻击方式下,各网络的能控性鲁棒性稍显不同,整体而言,QSNR和QSN 优于MCN,其中QSNR 又稍优于QSN[115].

随机三角形网络RTN[50,106]基于Henneberg 增长,由大量的有向三角形构成.将其扩展到四边形,就形成了随机四边形网络RRN[50].在这两个模型中,任意一个节点都至少处于一个三角形/四边形(有向环)当中.这些多环结构的存在,使它们的能控性鲁棒性较好.

极同质EH 网络[116]中任一节点i(i=1,2,···,N) 的出度和入度被限定在极小范围内,也就是

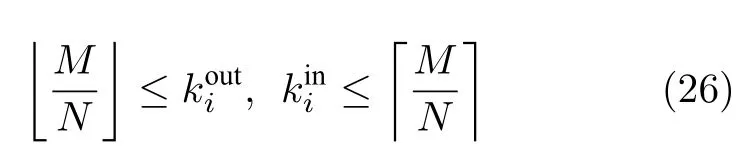
3.2 不同网络拓扑结构的能控性鲁棒性比较

Chen等[50]以第1.3.3 节基于排序的度量比较了包括随机图网络RG[103]、无标度网络SF[107−108]、同余网络MCN[122]、q-回路网络QSN[113−114]、随机三角形网络RTN[50, 106]和随机四边形网络RRN[50]等6种网络在6种不同攻击(包括随机节点和随机连边攻击,基于度数的节点和连边攻击,以及基于介数的节点和连边攻击)下的能控性鲁棒性,发现ER和RRN 能较好地抵御节点攻击,而RRN和RTN能较好地抵御各种连边攻击.

文献[115]通过实验比较得出当反向连边概率为0.5 时,QSNR 网络的能控性鲁棒性最佳,此时QSNR 的能控性鲁棒性优于QSN.

现有研究证实,极同质EH 网络[116]是在给定网络规模(N节点和M连边)情况下,能控性鲁棒性最优的结构(如图7 所示).同时,Lou等[116]提出的随机连边矫正RER (Random edge rectification)策略,可将任何网络结构,改变为EH 网络,同时,与EH 网络越近似则该网络的能控性鲁棒性越好.

表2 列举了几种能控性鲁棒性优化的网络结构.这些网络都由优化设计得到,其中QSNR和EH 需要进行重新连边优化.仅EH 结构具有全齐属性.除了MCN 仅具有多链结构,其余5种网络同时具有多链和多环结构.

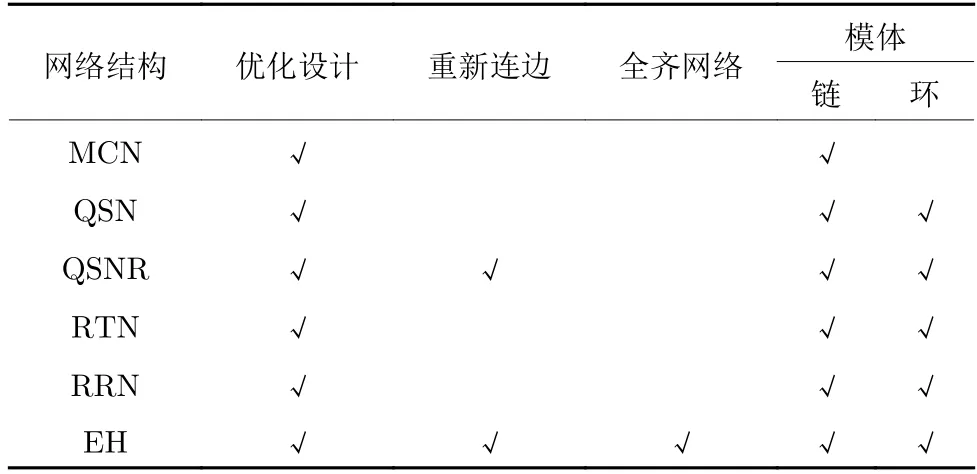
表2 能控性鲁棒性优化的网络结构Table 2 Comparison of network topologies with optimized controllability robustness

3.3 重新连边优化

重新连边(Rewiring)[119]通常分为3种形式:1)基于度保持(Degree-preserving)的重新连边: 保持各节点出度和入度不变,重新调整连边;2)保持网络基本骨架不变,对连边的方向进行调整;3)保持网络整体节点和连边数目不变,对网络进行任意重构.其中第1种方式为最常用的策略.本小节只讨论前两种方式,第3种将在第3.4 节讨论.不同的重新连边策略本质上是对式(22)的 Ω 进行了不同约束,而优化的目标是相同的.

重新连边常用于连通鲁棒性的优化.基于度保持的重新连边策略保持每个节点的出度和入度均不变,即将连边Aij和Ast(is或jt) 重新连接为Ait和Asj,从而保持节点i和s的出度不变;节点j和t的入度不变.异质网络 (例如无标度网络等) 在应用基于度保持的重新连边策略后,网络趋于洋葱型(Onion-like)结构,即度数相近的节点之间普遍连接,同时抑制度数相差较大的节点之间的连接,洋葱型网络具有较好的连通鲁棒性[36,110−112,123],同时也能提高网络的k-壳组成.

重新连边可看作优化问题,基于不同的目标函数,网络的优化趋向不同.Chan等[65]以谱度量[124−128]为目标函数,通过基于度保持的重新连边策略来优化连通鲁棒性.谱度量是常用的用于估算和预测复杂网络连通鲁棒性的工具[129].然而,目前尚未发现谱度量或其他复杂网络特征与能控性鲁棒性具有较强的相关性[49].

Xiao等[130]提出的基于度保持的重新连边策略首先选择特定度范围的4 个节点,然后交换其连边.该方法在增强网络连通鲁棒性的同时,也降低了网络同配性系数(Assortativity coefficient)[131].

Louzada等[132]提出的智慧重新连边(Smart rewiring)策略通过增强枢纽节点的相邻节点之间的联系,来增加网络抵御基于度数攻击的鲁棒性.该方法假设枢纽节点为首要攻击目标,很多情况下,当枢纽节点遭受攻击后,其相邻节点之间的联系随即消失.通过智慧重连策略可使枢纽节点遭受攻击后,网络仍保持较好的连通性.

启发式算法不仅应用于网络攻击(见第2.3 节),同时也应用于优化复杂网络鲁棒性.启发式算法包含一个种群的解,其中每个解代表一个网络结构,通过变异和交叉,以适当地选择算子来引导解的演化趋势,从而产生出高质量的解,即鲁棒性好的网络结构.

Buesser等[133]用模拟退火(Simulated annealing)算法来优化网络连通鲁棒性.Zhou等[134]以式(10)作为目标函数,用文化基因算法(Memetic algorithm)来优化无标度网络的连通鲁棒性.

由于抵御连边攻击的连通鲁棒性往往不能随着抵御节点攻击的鲁棒性的提高而提高[135],Zeng等[135]以混合贪婪算法(Hybrid greedy algorithm)来同时提高网络对抗节点攻击和连边攻击的连通鲁棒性.Liu等[136]提出了以多目标优化(Multi-objective optimization)来同时优化对抗节点攻击和连边攻击的鲁棒性.Wang等[137]以多目标优化,同时优化网络的连通鲁棒性和抵御级联故障的鲁棒性.多目标优化不仅可以优化网络的不同鲁棒性,同时连通鲁棒性的多种度量也可以被同时优化[138].Ma等[95]通过攻击和防守交替的策略提高网络鲁棒性,其中防守策略是指通过随机、优先或平衡的方式来补充被攻击的节点或连边.对于异质网络的连通鲁棒性优化来说,一个普遍共同结果是产生洋葱型结构网络[37,110−112].

与攻击方式一样,已有研究大部分侧重于提高连通鲁棒性.能控性鲁棒性的优化可借鉴连通鲁棒性的优化方法,但是由于评价标准和优化目标的不同,能控性鲁棒性的优化有其自身特点.通过删除冗余连边和增加关键或普通连边的方式[139−140],减少网络中非匹配节点数,可以提高复杂网络能控性.Wang等[141]以合作者比例(维持合作能力)和式(14)所示能控性鲁棒性定义作为两个优化目标,以多目标进化算法来同时优化它们.

Hou等[142]保持了网络的架构和规模(节点数和连边数)不变,通过只改变连边的方向来优化能控性.Lou等[115]通过改变非主链连边的方向,不仅将原先均匀度分布改变成泊松分布,同时也增加了模体的数量和跨度,提高了QSN 的能控性鲁棒性.虽然一般来讲,同质网络较异质网络具有较好的能控性和鲁棒性,但是同余网络的存在否定了这一共识结论[122].然而,Lou等[116]提出对于给定数量的节点和连边,能控性鲁棒性最优的网络结构(满足式(22))应具有极同质结构,即所有节点的出度和入度均相等(或者其差值小于等于1).Shi等[143]提出的全齐性(Totally homogeneous)网络给出了较极同质网络更为全面的数学定义,且提出全齐性网络具有最优同步性等多种最优指标.通常地,多链结构和多环结构具有较好的能控性鲁棒性[50,113,115,122].

3.4 全齐网络

基本的网络结构,如链式、环式、星型等结构无法解决一些新涌现的网络问题,如能控性网络子结构的设计和优化网络同步性等问题.Shi等[143]借鉴庞加莱的剖分思想,把网络分解为全齐性子网络.以团(Clique)为基本单位建立一系列二元域上的向量空间表述网络结构.模型和实际网络中都存在大量全齐性子网络,是支持网络功能的重要基础结构,对网络同步性[144]、能控性[18,33]、连通鲁棒性[37]等具有重要意义.Fan等[145]研究了网络的圈结构,提出刻画网络圈结构的边界矩阵和衡量节点重要性的圈指标.

Lou等[116]基于小规模网络的遍历搜索,归纳了经验必要条件ENC (Empirical necessary condition).ENC 指出满足式(22)的最优网络结构,应满足式(26).Lou等[116]发现对于给定N节点和M连边,其所有网络结构、满足ENC 的网络、以及最优网络之间的关系如图8 所示.

图8 所有N 节点和M 连边网络,满足ENC 的网络、全齐网络,以及最优网络之间的关系图Fig.8 The relationship diagram of theN-nodeM-edge networks,ENC networks,totally homogeneous networks,and the optimal networks

同时,Lou等[116]提出了随机连边矫正RER(Random edge rectification)策略,该策略使复杂网络趋于满足式(26)的结构,此外,使用RER 策略的次数与网络能控性鲁棒性的提高成正比.RER属于第3种重新连边优化方式,即保持网络整体节点数N和连边数M不变,对网络进行(任意)重构,以达到优化能控性鲁棒性的目的.

经验地,全齐网络满足ENC 条件,同时也是最优网络;然而显然并非所有的最优网络都属于全齐网络,其关系如图8 所示.

3.5 模体

模体(Motif)[146]是复杂网络中高频出现的具有统计意义的导出子图.近年来模体的研究广泛深入到各个领域,如电力系统网络[147]和大肠杆菌代谢网络[148]等.在网络控制方面,Badhwar等[149]发现秀丽线虫神经元网络中,前馈模体的数量对能控性的影响较大.Dey等[150]研究了不同攻击策略下网络中模体的变化情况,并分析了欧洲国家的电力系统网络的连通鲁棒性差异.贾承丰等[151]提出了基于模体的攻击策略,仿真结果表明基于模体攻击对模体特征明显的网络可造成的更大损害.

同余网络MCN[122]中存在较多链式模体结构.每一条链仅用一个控制器即可保证链路能控性.在受到攻击时,针对驱动节点的攻击不会破坏链路能控性;反而随机攻击更容易造成链路断裂,从而增加额外控制器.Lou等[113]进一步将链式模体扩展至环式模体.环式模体的反馈连接比链式的前馈连接具有更好的能控性鲁棒性.QSN 网络中含有大量的链式和环式模体[113].多模体结构的QSN和MCN在抵御攻击方面优于一般的无标度网络.进一步地,对QSN 的非主链连边随机反向重连可增加3-环、4-环和4-链(n-环/链指由n个节点构成的环/链)结构,增强了能控性鲁棒性.

Chen等[50]比较了具有链式模体的MCN,具有环式模体的QSN,以3-环为基础结构RTN,以4-环为基础结构的RRN 等在不同攻击下的能控性鲁棒性,发现3-环和4-环的RRN和RTN 结构在各种连边攻击下,保持较好的能控性.

4 展望与总结

本文围绕3 个问题进行归纳与总结:

1)复杂网络能控性鲁棒性的定义和度量.不同的定义因侧重点不同而稍有区别,须根据实际应用场景选取适当的定义和度量方式.

2)常见的复杂网络攻击方式及其对网络连通性和能控性的危害.随机攻击的危害较小,对攻击者来说需要掌握的网络相关信息较少;基于特征的蓄意攻击依据预先设定的特征对网络的节点或连边实施攻击,取得的攻击效果往往较好,对攻击者来说需要掌握较多网络相关信息;启发式攻击以智能计算优化攻击,往往需要具备较全面的网络相关信息和较多的计算资源,同时攻击效果的提升也较为显著.

3)能控性鲁棒性的优化问题.对于尚未建立的网络可采取优化建模,对于已有网络可采取(全部或部分)重新连边策略.如果能够掌握攻击者的信息,则可更有效地针对某一类攻击做出防御.一般的,在各类攻击情况下,极同质网络具有较好的能控性鲁棒性.

针对以上3 个问题,未来可研究内容包括:

1)深度学习和计算智能可更广泛地应用于复杂网络能控性鲁棒性的预测、分析和优化.目前,利用深度学习预测复杂网络能控性鲁棒性的研究和利用计算智能来生成优化网络拓扑结构的研究处于起步阶段.深度学习和计算智能处理大规模问题能力的进一步发展,将会对包括能控性鲁棒性在内的复杂网络各项研究带来新的机遇和挑战.

2)相关网络特征与能控性鲁棒性的相关性值得进一步探索和研究,包括相关拓扑结构特征、关键节点和关键连边的定义与搜索等.这一研究方向的难点在于网络规模、拓扑结构、攻击方式等同时具有多样性.同时,在实际网络中,各节点和连边存在权值等因素,因此,相对不容易形成一般性可泛化的理论结果.

3)全齐性网络和经验必要条件的进一步研究和理论拓展.全齐性网络和经验必要条件的研究从简单结构开始,逐步推向一般情况,简单的网络拓扑结构比一般实际网络更容易研究分析,实现理论突破.对经验必要条件的理论证明,以及对经验和理论充分条件的探索,将从理论上实现复杂网络能控性鲁棒性的最优化.

附录A 本文所用符号列表

A邻接矩阵

Aij邻接矩阵中节点i和j之间的连边

bi节点i的介数

B输入矩阵

C能控性矩阵

E网络连边集合

G复杂网络

ki节点i的度数

节点i的出度

节点i的入度

M网络连边数

Mc关键连边数

Mr当前已攻击的连边数

N网络节点数

ND网络所需控制节点数

∆ND网络所需控制节点数增量

Nr当前已攻击的节点数

nD网络所需控制节点密度

p(Mc)关键连边比例

Rc平均能控性鲁棒性

RLCC平均连通鲁棒性

u控制向量

V网络节点集合

x状态向量

σij从节点i到j的最短路径

Ω 适用解空间