一种面向工业过程的质量异常检测与故障量化评估方法

董洁 张伟 彭开香 马亮

质量异常的故障检测与量化评估技术是保证安全生产及获得可靠产品质量的有效手段,是当前国际过程控制领域的研究热点之一[1].复杂工业过程的非线性、高维度特性给其应用带来了极大的挑战.因此,有必要建立准确可靠的监测模型质量异常的故障诊断,为现场维护提供支持.

随着分布式控制系统(Distributed control systems,DCS)的广泛应用,多元统计过程监测(Multivariate statistical process monitoring,MSPM)方法得到了广泛的关注[2−3].主成分分析(Principal component analysis,PCA)作为MSPM 的典型方法,通过将高维空间分解为主元子空间和残差子空间,进而采用T2和平方预测误差(Square predicted error,SPE)统计量进行检测,近年来广泛地应用到故障检测领域[4−5].然而,基于PCA 的故障检测技术聚焦于故障是否发生,而忽略了由过程变量引起的故障是否会影响最终产品的质量.于是,以偏最小二乘(Partial least squares,PLS)、典型相关分析(Canonical correlation analysis,CCA)等为核心技术的质量异常检测(Quality abnormality detection,QAD)研究成果不断涌现.PLS 立足于两组变量之间的协方差最大化.近年来基于PLS 及其相关扩展模型的质量异常检测技术层出不穷.Zhou等[6]将PLS 提取过程变量中与质量相关空间的优势与主成分分析相结合,构建了全潜结构投影(Total-partial least squares,T-PLS)模型,实现了质量异常检测.Ding等[7]针对静态过程,提出了一种改进偏最小二乘(Modified partial least squares,MPLS)算法,提高了分解后子空间可解释性和关键性能指标检测能力.Huang等[8]通过核偏最小二乘法(Kernel partial least squares,KPLS)将主成分分析与质量异常检测相结合,提高了质量监测的有效性.Wang等[9]从模型鲁棒性的角度将正交信号校正(Orthogonal signal correction,OSC)与改进偏最小二乘(Modified partial least square,MPLS)方法相结合,提高了模型对微小故障的敏感性,增加了建模的复杂度,但其检测性能与MPLS相当.Jiang等[10]通过开发基于MATLAB 的面向关键性能指标的故障检测工具箱,对基于多变量统计分析的众多面向关键性能指标监测方法从建模原理、准确性、检测敏感性等多角度对比分析,进一步验证了MPLS 具有高计算效率,OSC-MPLS 具有良好的故障检测能力和灵敏性.与PLS不同的是,CCA 通过最大化两组变量的相关系数来获得质量相关的投影矩阵,取得了大量研究成果[11].Chen等[12]将CCA 应用于动态过程残差信号的构建,提高了模型对动态过程的检测性能.Zhang等[13]将CCA与分布式思想相结合,改善了传统的质量异常检测的效果.但是,复杂工业过程的数据往往具有非线性、非高斯等特性,传统的MSPM 方法遭遇一定瓶颈.支持向量数据描述(Support vector data description,SVDD)算法最早由Tax等[14]提出.由于其对具有非线性、非高斯特性的数据具有很好的适应能力,已经广泛地应用到复杂工业过程的故障检测领域.为了提高模型的检测能力,基于SVDD 的故障检测方法不断涌现.Khediri等[15]将核技术与SVDD相结合,实现了多模态过程的非线性故障检测.Zhang等[16]采用间隙度量进行数据预处理,实现了流程工业的厂级监控.Zhu等[17]采用粒子群优化算法对SVDD 进行改进,实现了检测模型的自适应更新,具有重要的现实意义.

故障检测虽然能够通过报警提示质量异常,但却不能给出故障根源、传播路径以及故障程度的量化信息.近年来国内外众多学者对相关问题进行了大量研究[18−19].但是,这些研究专注于故障根源与传播路径辨识,缺少对故障进行准确的量化评估,轻则造成维护费用的增加,重则会导致故障的蔓延和恶化.因此,不同于故障根源与传播路径辨识,对质量异常故障进行合理评估能够为维护人员提供更好的决策支持.Luo等[20]提出了一种采用两级判别指标的方案,将故障划分为严重故障、轻微故障和无害故障,实现了故障等级评估.Song等[21]将过程变量空间划分为3 个性能相关的子空间,并在此基础上进行了故障的严重程度分析.Yang等[22]在操作性能评估的过程中采用加权主成分分析(Weighted principal component analysis,WPCA)的方法针对系统不同的性能状态分别建立检测模型,采用T2统计量构建健康指标,实现了对系统状态的等级划分.以上方法虽然能够从检测的角度对故障进行分析,但是并没有给出精确的量化评估结果.为此,Guo等[23]采用拉普拉斯特征映射(Laplacian eigenmap,LE)进行低维投影,得到了更加准确的退化指标.Yan等[24]在评估指标的构建过程中综合考虑不同操作条件,实现了多工况的状态监测.Sun等[25]在设备健康监测中采用了核稀疏表示的局部线性嵌入算法(Kernel sparse representation–local linear embedding algorithm,KS-LLE)对轴承的不同故障程度进行了量化评估,得到了良好的评估效果.Atamuradov等[26]采用基于特征融合的监测方法,实现了电机系统的状态评估.上述方法虽然能够实现量化评估,但并未分辨出故障是否造成质量异常,进而不能提供准确合理的维护建议.

针对上述问题,本文提出了一种新的工业过程质量异常检测与故障量化评估(Fault quantitative assessment,FQA)方法.对比已有的工作,本文的主要贡献归纳如下: 1)采用弹性网络(Elastic net,EN)算法构建了更加可靠的质量相关的变量候选集,能够为后续的检测与评估提供支持;2) 采用CCA 算法强化了候选集变量与质量变量的关系,并通过SVDD 实现了质量异常检测;3)从优化近邻点距离的角度改进了局部线性嵌入(Local linear embedding,LLE)算法,并提出了CCA-ELLE 算法,将质量异常的故障样本投影到二维空间进行量化分析,实现了准确的故障量化评估.

1 基于CCA-SVDD 的质量异常的故障检测方法

1.1 质量相关的变量候选集

复杂工业过程测量变量较多,变量间存在多重共线性.为了降低候选变量集的信息冗余,需要对过程变量进行特征选择.为了更好地结合质量相关信息,考虑采用正则化的方法进行变量选择.

给定输入矩阵X∈Rn×m,n为样本个数,m为变量维数,Y∈Rn×1代表输出变量.x∈R1×m,y∈R1×1为样本在X和Y中对应的元素.标准的最小二乘算法的思想是最小化残差平方和

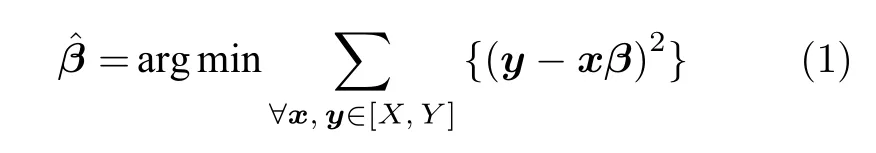
式中,s决定EN 的收缩程度.当s →0 时全部的变量会被消除.相反,当s →∞时算法逼近标准的最小二乘算法.参数η可以调节两种惩罚项的权重,当η=1 时该算法为基本的岭回归算法,当η=0 时为基本的LASSO 算法.本文将过程变量作为EN算法的输入变量,质量变量作为输出变量,通过合理选择收缩参数s,构建质量相关的最优变量候选集.

1.2 CCA-SVDD 算法

为了增强过程变量与质量变量的关系,同时降低数据的多重共线性,采用CCA 算法构建质量相关的特征矩阵.首先,获得一对投影向量α和β,使得随机变量u=αTX与v=βTY具有最大的相关系数ρ=corr(u,v).目标函数为

式中,特征值λ为随机变量u与v的相关系数.由于特征矩阵由过程变量构成,因此只需计算投影向量α.

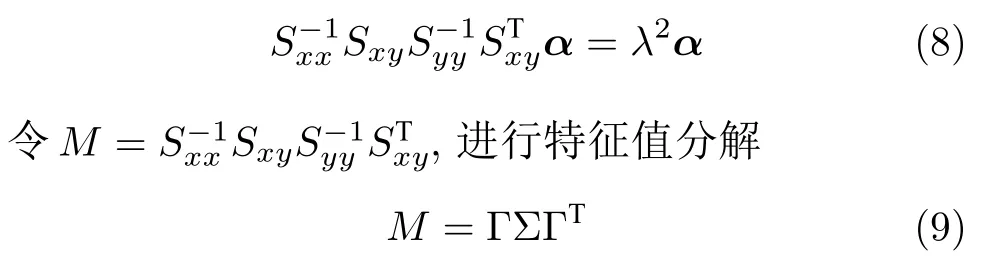
取最大的前d项特征值对应的特征向量作为投影向量

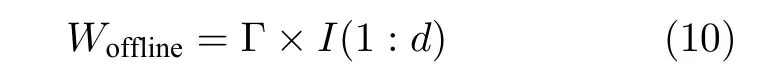
其中,I(1:d) 为d维单位矩阵,Woffline∈Rp×d,p为变量维度,d为投影变量的维度.

在线测试阶段,测试样本Xtest经过如下处理:

式中,C可以调节容错率,R为超球体的半径,a为超球体的中心.通过拉格朗日乘子法并转化为对偶问题,则目标函数转化为

式中,σi(i=1,···,n) 为样本ui对应的拉格朗日乘子.σi0 的样本称为支持向量.內积的计算引入了核函数 (ui,uj)=exp(−∥ui −uj∥/ρ2),参数ρ可根据经验调节.因此,得到超球体中心a和半径R

于是,测试样本是否为故障状态可以通过如下方式判别:

2 基于CCA-ELLE 的故障量化评估方法

2.1 增强LLE (ELLE)算法

给定测试样本的最优典型相关变量集Utest∈Rl×d,计算如下:

式中,l代表测试样本数量.LLE 算法包括以下3个步骤[24]:

步骤1.获取每个样本的近邻点集合.样本的近邻点集合包含k项元素,可以通过k近邻的方法得到.

步骤2.计算样本与其近邻点的连接权重w,可以通过最小化重构误差

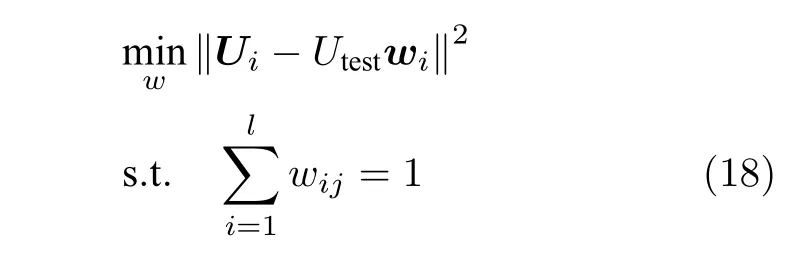
得到权重矩阵W∈Rl×l,其中,Ui∈Utest为选取的样本近邻点,wi为近邻点对应的权重向量.在权重矩阵的取值过程中,不属于近邻域的样本权重为零.在接下来的运算过程中W保持不变.

步骤3.给定yi为Ui的低维空间投影,通过最小化重构误差得到目标函数

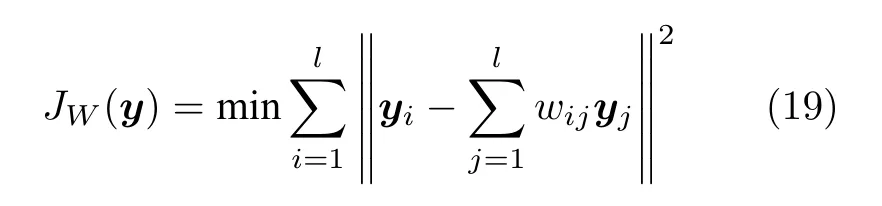
目标函数等价于

LLE 算法只考虑了重构误差,计算权值的条件为近邻点之间保持线性关系,也就是只考虑了近邻点间的拓扑结构.在构建近邻点集合之后,并没有考虑样本数据与其近邻点的距离信息.因此,样本点与其距离较小的近邻点的权重可能会比与较远距离近邻点的权重小.这将会导致通过LLE 建立的模型不准确,并且会严重影响评估的准确性.

为此,本文提出了增强LLE (Enhansed LLE,ELLE)算法.建立如下目标函数

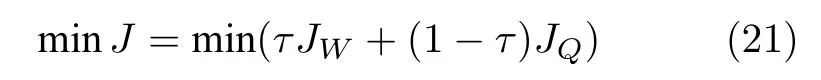
式中,JW是LLE 算法的目标函数.JQ为反映近邻点与样本点距离的目标函数,τ为调节两部分权重的参数.矩阵化表示为

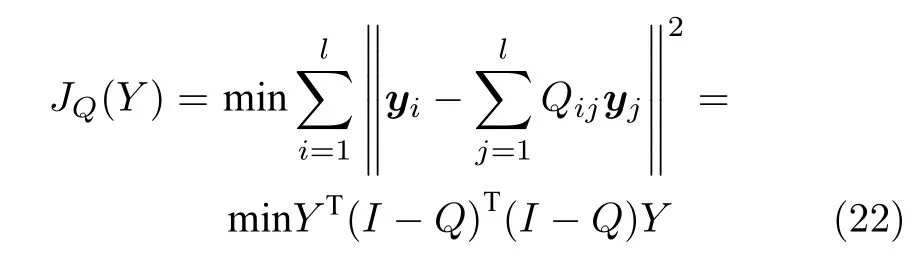
式中,Q∈Rl×l表示样本点与其近邻点距离的权重矩阵.为了提高算法对非线性数据的处理能力,Q矩阵元素的计算引入了核方法

其中,Ui和Uj为不同样本点.权重矩阵Q增强了样本点与其近邻点的距离.由于距离的计算函数为减函数,距离较小的近邻点对应的值相比于距离较远的近邻点对应的值更大.参数δ可以调节衰减率.

ELLE 算法的目标函数表示为

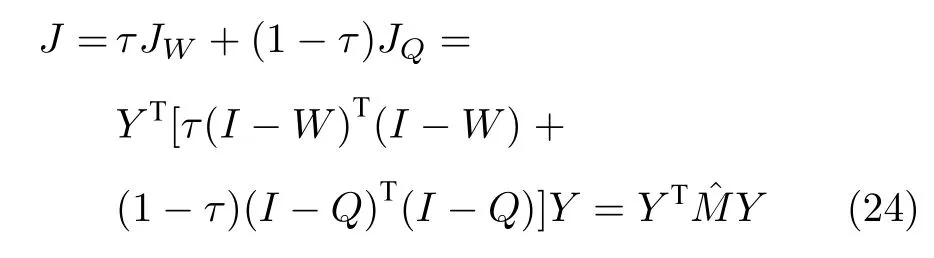
后续的计算过程与LLE 算法相同.

2.2 量化评估指标的构建

与LLE 算法类似,ELLE 算法会保留原始数据的拓扑结构,低维数据保留着高维数据的局部几何结构.定义正常状态的样本中心点与原点构成的方向向量为,测试样本点与原点构成的方向向量为.定义,故障的严重程度指标定义为SI(i),取值范围为 [ 0◦,360◦].计算方法为

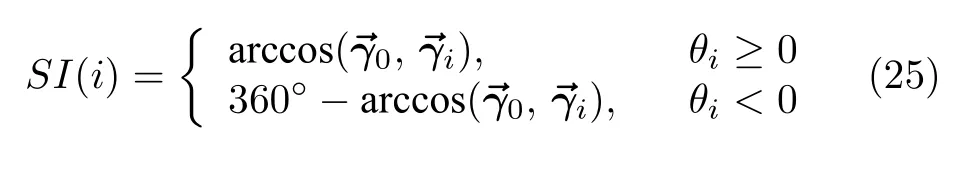
其中,arccos(·,·) 为两方向向量内积的反余弦函数,此处计算的值为角度.由于故障程度定义在二维空间,指标计算要在 [ 0◦,360◦] 的范围内.评估方法示意图如图1 所示,样本故障程度满足SI(2)>SI(1).为了更直观地进行比较,使评估结果更具有普遍意义,同时提高评估结果的精度和可靠性,采用每一种状态的样本中心点代表当前状态,对评估结果进行归一化.

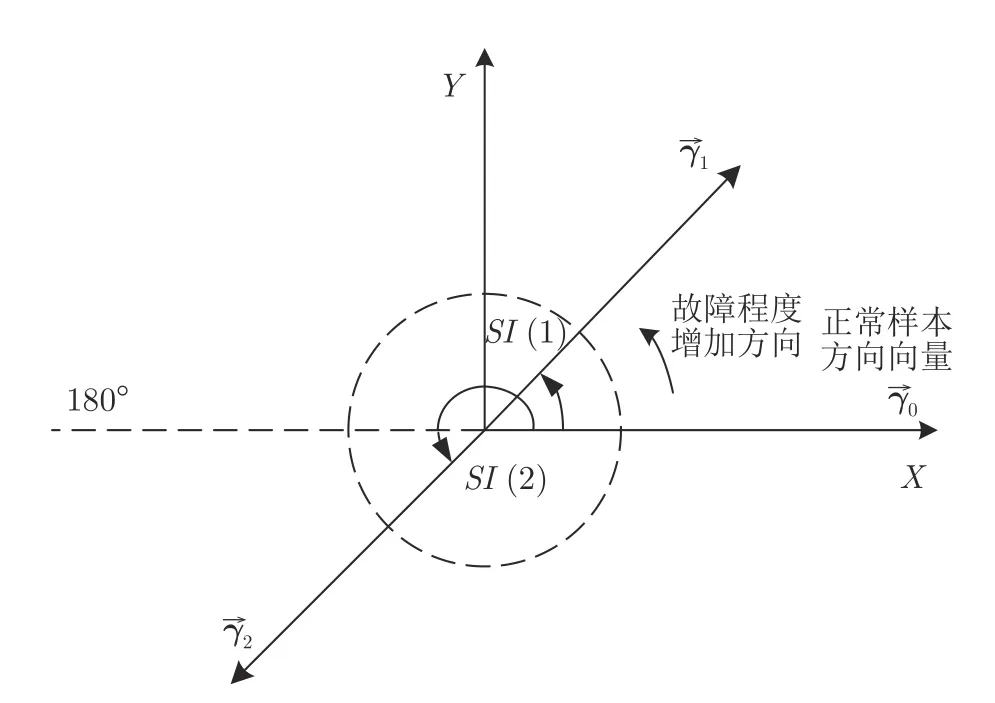
图1 评估指标示意图Fig.1 Schematic diagram of evaluation indicator

2.3 质量异常检测与故障量化评估流程

本文提出的质量异常检测与故障量化评估框架包含离线建模和在线检测两部分.

2.3.1 离线阶段

1)获取正常状态的过程数据,并进行数据预处理(z-score 标准化,数据平滑处理).

2)采用EN 算法构建质量相关的变量候选集,为之后的质量异常检测与故障量化评估提供支持.

3)采用CCA 算法获得投影矩阵Woffline∈Rp×d和变量集Uopt,同时将Uopt送入SVDD 模型中训练检测模型.

2.3.2 在线阶段

1)获取测试数据Xtest∈Rl×p,并进行数据预处理(z-score 标准化,数据平滑处理).

2)送入已建立的CCA 模型,获得典型相关特征矩阵Utest∈Rl×d,进而送入SVDD 模型进行判别.根据式(16)的计算结果,如果出现质量异常,则进行下一步,否则,继续执行检测部分.

3)采用ELLE 进行投影,得到二维空间表示的样本Ytest∈Rl×2,进而获得表征测试样本的方向向量和表征正常样本的方向向量.

4)计算测试样本间方向向量的夹角,即故障的量化评估指标SI(i).

所提方案的流程图如图2 所示.

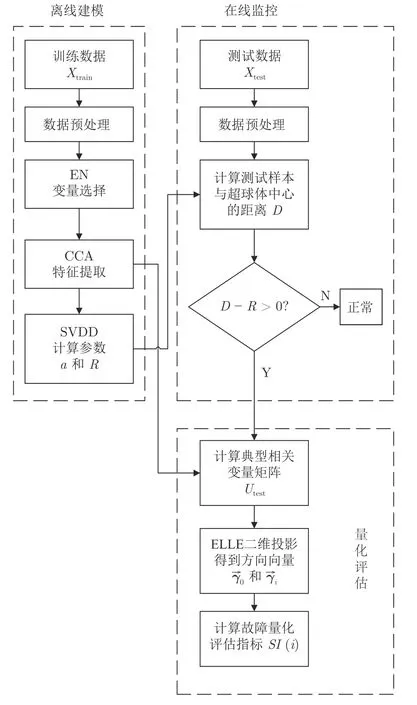
图2 质量异常检测与故障量化评估流程图Fig.2 Flowchart of QAD and FQE

3 仿真研究

3.1 TE 过程描述

TE (Tennessee-Eastman)过程由5 个主要单元: 反应器、冷凝器、压缩机、分离器、汽提塔组成;存在8种成分,其中,A,B,C,D,E 为反应物,G,H 为产物,F 为副产物[28].本文的实验是在模态1 的基础上完成的.22 个过程变量作为过程监测的目标变量,详细情况见表1.TE 过程的Simulink 仿真模型含有28 中不同的故障类型,每一种故障可以通过设置参数来决定是否注入.对同一种类型的故障可以通过设置参数来调节注入故障的严重程度(Fault severity,FS),FS 的调节范围为 [ 0,1],代表过程从 FS=0 到 FS=1 的不同状态.

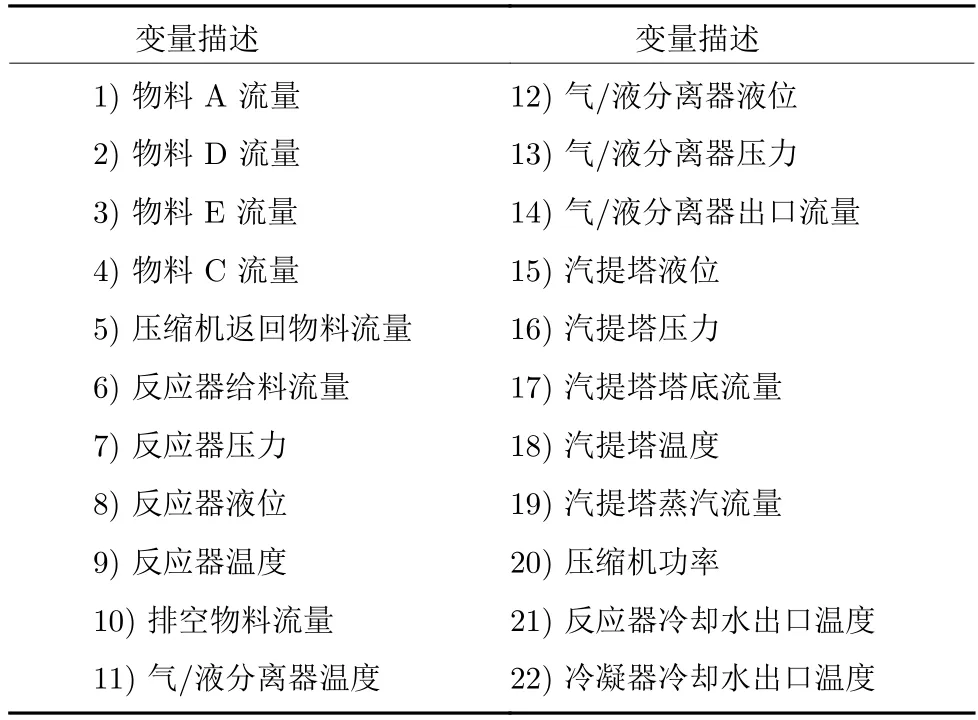
表1 TE 过程变量Table 1 Process variables in the TE process

3.2 参数分析

本文提出的算法存在两个主要参数: 特征维数d和近邻点数量k.下面分别讨论各参数对算法评估效果的影响.

1) CCA 特征融合后的特征维数d

较少的特征维数会破坏原始数据的近邻结构,而维数较高则会引入冗余信息.在参数分析过程中,分别将d设置为3,4,5,6,7.仿真结果见图3(a).

图3 参数分析Fig.3 Analysis of parameters

2)近邻点数量k

近邻点选择较少会破坏原始数据的近邻结构,近邻点选择较多则会忽略数据的局部特征.在参数分析过程中,分别将k设置为16,18,20,22,24.仿真结果如图3(b).

图3 中横坐标代表从 FS=0 到 FS=1 的6种不同的故障工况,纵坐标代表量化评估结果.为了进行准确的量化评估,评估结果需要满足两个条件:1)不同过程状态的评估结果需符合实际故障程度;2)相邻过程状态的评估结果间隔均匀.可以看出,图3(a)中d=5 的曲线和图3(b)中k=20 的曲线均为最优情况.因此本文的特征维数设置为d=5,近邻点数量设置为k=20.

3.3 实验结果

采用EN 算法对正常状态的数据样本进行分析,选取产物G 的成分含量作为质量变量,式(5)中的参数设置为η=0.2,构建了质量相关的最优变量候选集X={x1,x2,x3,x4,x7,x10,x13,x20,x21}.为了验证所提方案,本文选取TE 过程标准故障类型2 进行验证,通过对TE 过程注入不同程度的故障,获得了相应的测试数据.具体情况见表2.

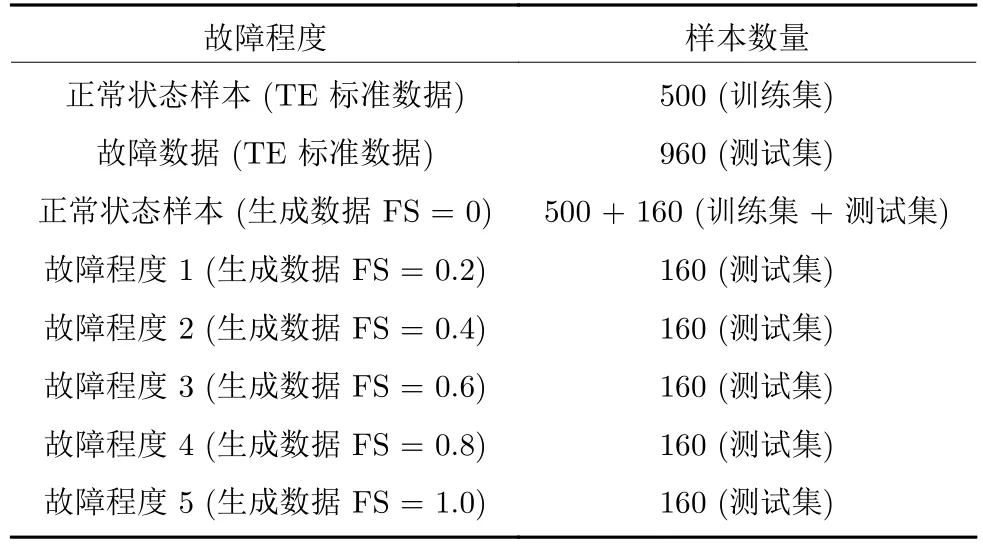
表2 验证数据集Table 2 Data sets used for validation

为了验证CCA-SVDD 算法的有效性和优越性,选择广泛应用于质量异常检测的KPLS 算法进行对比,控制限的置信度设置为95%.两种方法检测结果如图4 所示.

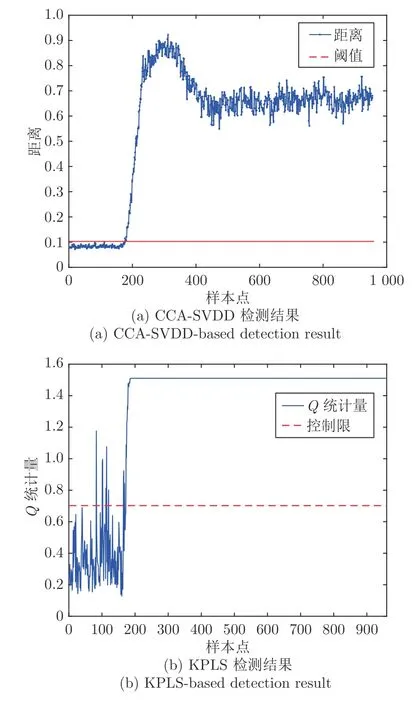
图4 两种方法的故障检测结果Fig.4 Detection results of the two methods

从表3 的对比结果可以看出,传统的KPLS 方法存在较高的误报率,而本文提出的CCA-SVDD算法在保证高检测率与较低计算复杂度的前提下,大大降低了误报率,检测效果良好.上述实验均在MATLAB R2019b 平台上完成,硬件配置为: i5@1.6 GHz,RAM 6 GB.

表3 两种方法的性能比较Table 3 Comparison of the two methods

为了验证所提故障量化评估方案的有效性,本文采用TE 过程标准故障类型2 进行验证,式(25)的参数设置为τ=0.8.表2 中的生成故障数据集对应的FD 值满足递增的关系.

首先,采用TE 过程标准故障类型2 进行验证.将正常状态(*)与故障状态(·)的数据用两种标识符号来表示,从图5 中可以看出,两种状态的样本点具有清晰的样本中心,并且故障状态样本点的分布说明了过程从正常状态到故障状态是有向分布的,而且样本点与原点构成的方向向量能够很好地反映状态的转变过程.

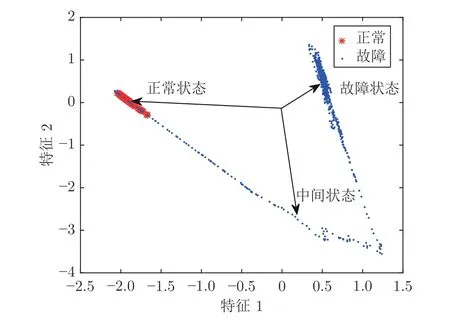
图5 CCA-ELLE 二维投影Fig.5 CCA-ELLE-based two-dimensional projection

图6 是通过TE 模型生成的不同程度故障数据对所提方案进行验证的结果.图中不同的故障程度采用不同类型的标识符号表示.可以看出,随着故障程度的不断增加,测试样本点与原点构成的方向向量具有连续变化的趋势,并且随着数据的不断延伸,不同类型的样本点可清晰地分开.

图6 两种方法的二维投影Fig.6 Two-dimensional projection results of the two methods

图7(a)和图7(b)为两种方法的量化评估结果.图7 (c)和图7(d)为归一化的评估结果.可以看出,评估指标越接近1,故障状态偏离正常状态越大,故障程度越高.并且传统的LLE 算法对于故障程度4 的评估结果与案例不符.而本文改进的CCAELLE 算法可以准确地量化评估不同程度的故障,而且不同程度的故障样本点的间隔较均匀,与验证案例相符.

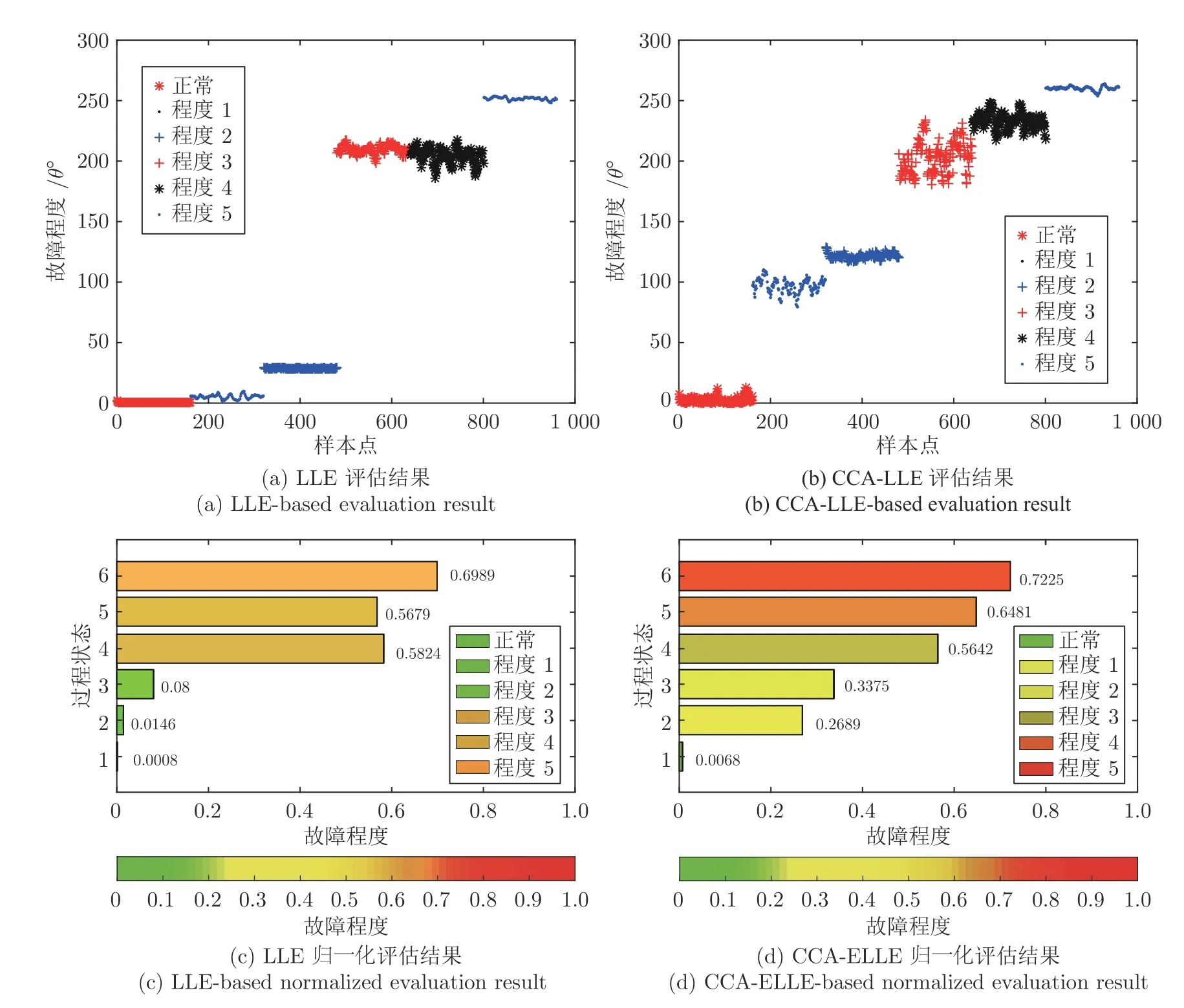
图7 两种方法的量化评估结果Fig.7 Evaluation results of the two methods

4 结束语

本文提出了一种新的工业过程质量异常检测与量化评估框架.首先,采用弹性网络算法筛选出可靠的质量相关的变量候选集;其次,提出了CCASVDD 算法进行质量异常监测,并取得良好效果;再次,从优化近邻点距离的角度提出了ELLE 算法,并与CCA 相结合实现了质量异常故障的量化评估;最后,通过TE 过程进行仿真验证,并与传统的方法进行对比分析,实验结果验证了所提方法的优越性和有效性.下一步的工作是将所提框架应用到多故障多种程度的质量异常检测与故障量化评估中.