基于蠕虫传播和FDI 的电力信息物理协同攻击策略

冯晓萌 孙秋野 王冰玉 高嘉文

随着电力系统和通信技术的高度耦合[1−2],远程攻击者可以利用漏洞入侵信息网络引起通信故障,进一步导致电力系统连锁故障.近年来,针对电力系统的攻击事件频繁发生,如2019 年3 月,委内瑞拉的古里水电站遭到反派黑客的网络攻击.2019年7 月,美国纽约曼哈顿发生了大规模停电事故.因此,电力系统的网络安全问题逐渐成为研究焦点.

现阶段针对电力系统网络攻击的相关研究可以根据攻击阶段的不同,分为2 类: 第1 类是在侵入电力系统前,研究针对通信层的攻击,即远程攻击者采取何种网络攻击方式入侵通信网络.这类研究在计算机科学领域已经相对完善,一般采用攻击树模型[3]和复杂网络理论两种方法对不同种类的攻击方法进行建模,如蠕虫攻击[4]、木马攻击和网络监听等.这类攻击不考虑从通信网络侵入后对电力系统造成的破坏.第2 类是在成功侵入后,研究针对电力层的攻击,即攻击者采用何种攻击行为破坏电力系统.这类研究主要是围绕如何篡改量测数据,从而躲避检测机理,对电力系统造成更严重破坏展开.主要包括: 虚假数据注入攻击(False data injection,FDI)[5−7]、负载重分配攻击(Load redistribution,LR)[8]和拒绝服务攻击[9]等.这类攻击不考虑攻击者利用通信设备上漏洞的难易程度和攻击代价.上述两类研究都相对独立,不能将攻击者如何侵入系统,和侵入后的攻击行为两个阶段联合为一个整体,实现跨空间攻击过程.为了探索两个阶段攻击行为的耦合过程,信息物理协同攻击逐渐受到国内外学者关注.与传统的网络或物理攻击相比,协同攻击的特点是同时考虑(由于物理攻击)对电力系统造成的破坏性,和(由于网络攻击)对通信数据造成的不准确性(篡改量测数据、开关状态等)[10].协同攻击的最新示例是2015 年12 月对乌克兰电网的攻击,该攻击使几台断路器(即物理攻击)断开,导致大约225 000 名客户断电.在攻击过程中,针对电力客户服务的分布式拒绝服务攻击[11]和KillDisk 服务器擦除(即网络攻击)被用来掩盖紧急情况并延长中断时间[12].

现阶段对信息物理协同攻击的研究处于初步阶段,主要分为2 类: 1) 攻击者能够通过网络攻击对物理攻击行为进行遮掩,欺骗检测机制.例如,通过FDI 攻击,修改线路的开断信息和量测数据,从而掩盖和误导调度中心错误指令.2)攻击者通过分析信息物理耦合网络的特征和双向跨空间级联故障传播特性,对耦合系统存在的漏洞进行分析,制定更有效的攻击方案[13−15].文献[16]提出了一种电力信息物理协同攻击分析模型,侧重于考虑攻击者和调度中心的交互关系.文献[17−18]分别分析了在可观察和不可观察条件下攻击者通过改变拓扑信息来掩盖物理攻击行为.文献[19]提出了一种在攻击者通过修改PMU (Phasor measurement unit)的量测数据后引起电力系统的状态估计结果出现误差的情形下,电力系统的脆弱性评判指标.文献[20]提出了攻击者共谋理论,某通信节点的量测数据和与它邻接的其他通信节点,即共谋者的数据同时被篡改后,更容易避开检测装置的检测机制.

当黑客进行协同攻击时会根据电力系统的网络结构、设备特性和破坏情况反馈制定最优的攻击策略.为了解决求最优解时出现的维度灾难、不连续可微函数不可解等问题,引入了人工智能算法[21].因为电力信息物理系统在信息物理协同攻击下的系统运行状态符合马尔科夫决策过程,提出了一种基于Q 学习方法求解的最佳攻击策略[22].文献[19]使用马尔科夫决策过程来模拟在电力信息物理系统中的攻击风险传播过程,并分析攻击者的攻击路线选择策略,以获得最佳的回报效益.此外,从攻防双方的角度出发,文献[23−24]建立了基于随机博弈的攻防模型,能够给防御资源分配起到指导作用.

类比电力系统中的级联故障[25],通信网络中故障的传播也具有一定的拓扑传染特性[13].上述研究均假设攻击者能够直接对从PMU 采集到的量测数据进行篡改,没有考虑信息层故障在通信网络中扩散到指定的量测设备这一阶段的拓扑传染机制,未实现跨空间协同攻击的耦合建模.因此,本文主要工作如下: 1)本文提出了基于马尔科夫决策过程的协同攻击模型,其在传统的虚假数据注入攻击的上层首次引入了蠕虫传播模型(Susceptible infected recovered model,SIR),实现了通信−电力双层攻击的耦合建模.2)在信息层采用漏洞评分标准(Common vulnerability scoring system,CVSS)中的 “漏洞利用难度”字段量化攻击者对攻击的难易程度,即攻击成本.在物理层依据全量测状态估计的误差值评定该攻击行为对电力系统造成的破坏程度,即攻击收益.3)使用Q 学习方法对该模型下攻击者最优协同攻击策略进行求解,目标函数定义为破坏电力设备的攻击收益和入侵通信层设备的攻击成本比值的积累奖励.4)使用网络模拟器(Network simulator 2,NS2)和MATLAB 进行通信8 节点−电力IEEE 14 节点的联合仿真实验,模拟攻击者跨空间渗透的攻击过程,并分析了在该最优攻击策略下相关设备被攻击的可能性.仿真结果表明,较单层攻击模式,本文所提的协同攻击模型攻击破坏性更强.本文进一步分析了最优攻击策略下相关设备被攻击的可能性,能更有效地发现电网薄弱环节.

1 电力信息物理跨空间协同攻击模型

近年来数例典型电网破坏事件[12, 26]的流程可以概括为: 远程黑客利用PC 机或可编程逻辑控制器(Programmable logic controller,PLC)中的系统漏洞注入病毒;该病毒在通信设备中级联渗透;扩散到指定功能的通讯设备或调度中心;随后通过修改量测数据和控制命令使得电力系统瘫痪.

如图1 所示,电力信息物理系统由电力系统网架结构和通信网络组成.量测装置PMU 将潮流和线路开关状态信息传输给由通信设备(如PLC)组成的通信网络,接着传输至调度中心.调度中心利用状态估计筛查量测数据,并进行潮流调度.基于此,本文提出了一种信息物理协同攻击模型,该模型实现了跨空间双层攻击的耦合建模,在上层通信层攻击模型建立为蠕虫传播模型,下层电力层采用虚假数据注入的攻击方式.通信−电力两层之间以电力母线上装置的量测装置PMU与PLC 等通信设备相连接.该协同攻击的攻击原理为: 远程攻击者发起蠕虫病毒感染通信网络中的PLC 等通讯设备.一旦感染成功,被感染的通讯设备所收集到的PMU 量测数据有一定概率被注入虚假数据,进而导致电力系统状态估计值出现误差,从而引发连锁故障.

图1 电力信息物理协同攻击示意图Fig.1 Diagram of electrical cyber-physical cooperative attacks

由此,本节首先对通信层和物理层攻击模式分层建模.然后根据网络攻击从信息系统渗透到物理系统的跨空间传播方式,提出了一种基于马尔科夫过程的协同攻击模型.为了便于表述,在下文中,将通信网络(C-net)中负责传输PMU 量测数据的通信设备定义为信息节点C-n,节点数目为Nc.将电力网络(G-net)中的母线抽象定义为电力节点Bus-n,节点数目为Ng.

1.1 通信层攻击模型

本节使用SIR 传染病模型对蠕虫病毒在通信层设备间的传播机制进行建模,并采用CVSS 漏洞评分标准来定义攻击者成本函数.

1.1.1 蠕虫传播模型

首例工业控制蠕虫病毒Stuxnet[27]被证实能在边缘通信设备,如PLC 中单独传播,不需要借助任何PC 机.文献[4]对工控网络中PLC 病毒传播机理进行建模,但仅分析了病毒在信息设备的传播机理.文献[28]使用元胞自动机建模定性分析了电力信息系统中信息安全风险跨空间传播的基本原理,但并没有给出具体模型.本文采用SIR 传染病模型对蠕虫病毒在电力通信网络中的传播机理进行建模.在该模型下通信设备i的状态有3种: 1)易感染态 (S): 易感染态也是正常状态,处于该状态的设备上存在安全漏洞,但还没有被感染节点扫描到.2)感染态(I): 此类设备已经成为蠕虫节点,将会扫描与它拓扑相连的其他易感染态节点并将其感染.3)免疫态(R): 此类节点的安全漏洞已经被修复,在该状态下对蠕虫节点的扩散免疫.通信网络中3种节点的状态转移过程如图2 所示,一旦某通信设备被感染成为蠕虫节点,那么攻击者可以获取该设备的权限,对该设备存储和传输的PMU 量测数据进行篡改.

图2 通信网络的SIR 蠕虫扩散模型状态转换图Fig.2 SIR worm diffusion model state transition diagram of the cyber network

如图2 所示,通信网络的设备状态转变和前一时刻状态的关联度较高.基于本模型的各个通信设备i从t时刻的状态到t+1 时刻的状态的状态转移概率为

其中,通信设备i在t时刻为易感染态(S)且t+1时刻为感染态(I)时,状态转移概率为,其他同理.该转移概率与通信网络当前的拓扑结构,数据包传输情况以及各个设备当前的感染情况有关.其中拓扑结构与网络中节点的度有关,本文将定义为信息节点i的度,表示该节点与个信息节点邻接.第i个信息节点在t时刻状态转移概率计算式为

其中,|Θi|代表与信息节点i相连接的蠕虫节点的个数.η是蠕虫病毒节点可以在1 s 内扫描的邻接设备的数量,该参数受限于扫描方法的性能和网络带宽.在理想的情况下,一般取实际网络带宽的上限.本节假设在同一个通信网络中全网蠕虫节点的值相同. ∆t表示扫描周期,这里设一般取为秒级.β代表通信设备扫描到一次之后被成功感染的概率.ς代表从免疫态(R)到易感染态(S)的恢复率,该参数是由病毒实时更新速度和补丁失效情况决定.同理,ν代表通信设备状态从感染态(I)转移到免疫态(R)的移除率,该参数是由漏洞补丁的更新速度和感染区域隔离情况等决定.

在实际情形中,攻击者通过监听和流量监测等手段并不能完全掌握观测到整个信息层设备的状态,只能掌握部分可观的网络结构、蠕虫节点的总数量和被监听的节点的连接信息,不能掌握正常节点和蠕虫节点的拓扑关联信息.下面对|Θi|进行估算,进而求解状态转移概率.本文根据已知参数估计通信网络的平均度估计各个信息节点的邻接情况.

通过攻击者检测到的相关信息,预估计出的度为k的信息节点的数为其中蠕虫节点的个数为表示该网络中的度分布,即节点度的散布情况.也就是说,在网络中随机抽取某信息节点的度是k的概率为λc(k).令⟨k⟩c代表平均度,可计算为

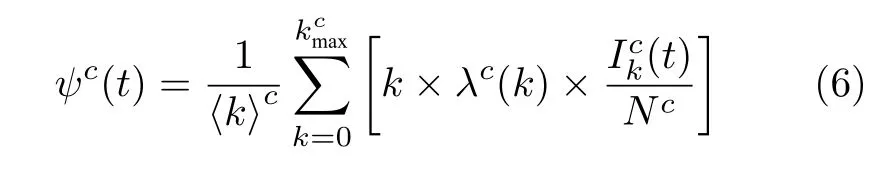
由此,|Θi|可以表示为

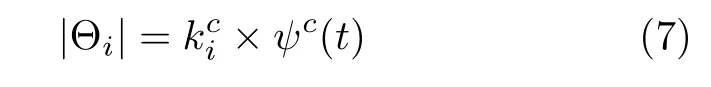
在该模型下可以模拟蠕虫病毒在通信网络中的传播机理.在这种动态的状态转化过程中,各个通信设备的攻击成本也随着状态转移概率动态变化.

1.1.2 攻击者成本函数

攻击者的攻击成本与设备主机上的漏洞的利用难度成正比.某一通信设备的攻击成本由该设备上最薄弱的漏洞利用难度决定.本文参考漏洞评估系统(CVSS)中网络漏洞评价指标的 “利用复杂性”分数,对漏洞难度量化.“利用复杂性”值越大,该漏洞被利用的难度就越大.此外,通信设备中的相关漏洞参数由工业互联网安全响应数据库[20]中提供.攻击者在t时刻攻击第i个通信设备的攻击成本为

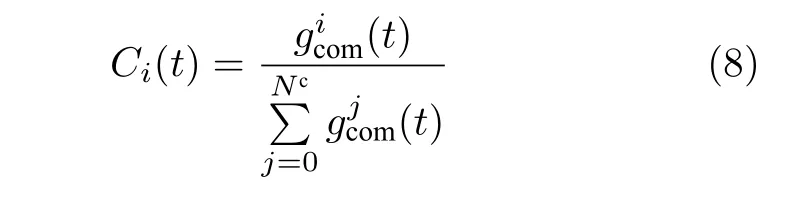
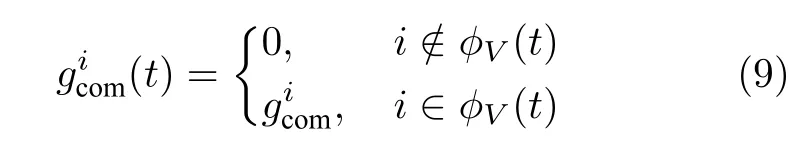
其中,ϕV(t) 代表暴露给攻击者的扫描目标集,即攻击者可以通过当前信息网络的渗透状态能够选择的下一个阶段攻击的目标节点的集合.本文使用动态攻击图G=(ϕV(t),ϕE(t)) 来记录攻击者的扫描目标集和渗透路径.ϕE(t) 代表攻击者掌握的当前扫描目标集能够利用的渗透路径.攻击图节点集ϕV(t)和边集ϕE(t) 的初值为攻击者在最开始时能利用的扫描网络.当蠕虫病毒扫描网络时,只能感染扫描集中的设备.一旦某设备i被感染,那么与其相邻的节点j,即满足lc,ij=1,会被加入ϕV(t),见式(17).同时,节点i和j的连接线将被添加到ϕE(t) 中.每一次攻击结束后,更新整个动态攻击图的拓扑.

1.2 电力层攻击模型

本节定义了电力系统全量测状态估计遭受FDI攻击后的错误估计结果和原始估计结果的均方误差(Root mean squared error,RMSE)作为攻击者攻击回报函数.分析了攻击者在篡改量测数据时,要同时更新共谋者的相关数据,以此躲避检测器检测机理.

1.2.1 电力系统的FDI 攻击

无论攻击者对信息层设备的渗透严重程度如何,其最终目标都是通过对量测装置、相关的控制设备和通信网络注入错误数据,进而导致电力系统状态估计器产生错误的状态估计结果,最终对电力系统相关应用业务造成危害.

本文采用电力系统全量测状态估计方法[29],该方法中电力系统状态估计的量测值包括SCADA量测值和PMU 量测值.从攻击动机方面,相比于SCADA 量测数据,PMU 量测量误差更小,精度更高,还包括独有的相角量测数据,具有很高的攻击价值.从攻击难度方面,考虑电力系统调度的分区机制,SCADA 在一区,防御最严密,攻入难度较大,而与PMU 量测量相关的通信设备由于在终端,攻入难度相对较小.综上,PMU 量测量更容易成为攻击者的攻击目标[30−31].基于此,针对全量测状态估计方法的电力系统虚假数据注入攻击过程如下:

步骤 1.首先使用传统的状态估计模型求解,即使用SCADA 量测数据计算加权最小二乘估计方法求解状态估计结果x(1)=[θ,V]T.

步骤 2.引入PMU 的量测值进行全量测状态估计

1.2.2 “共谋” 躲避检测机理

对电力节点j的第l个量测值zjl注入虚假数据后,该错误量测数据被检测器检测出的概率与检测算法和该节点周围邻接节点的量测值被篡改的个数有关[33].该节点周围邻接节点的量测值被篡改的个数越多,对该节点注入恶意数据后被检测出来的概率越小,即攻击者共谋理论.本节对这个特性进行定性分析检测器检测概率,某个电力节点j数据被篡改后,被检测出来的概率为

1.2.3 攻击者回报函数

假设攻击者某一次的攻击行为成功地避开了检测机制,将合适的虚假数据注入系统的量测装置并且造成估计的状态结果的偏差,则攻击者可以通过本次攻击行为获得回报.对于某一个电力节点j的数据被篡改之后,攻击者攻击回报为电压偏差和电流偏差,即

其中,Vxj,θxj分别是原始估计结果,而是错误的估计结果.针对整个电力网络,攻击者的攻击收益为全局状态估计结果的均方根误差,即

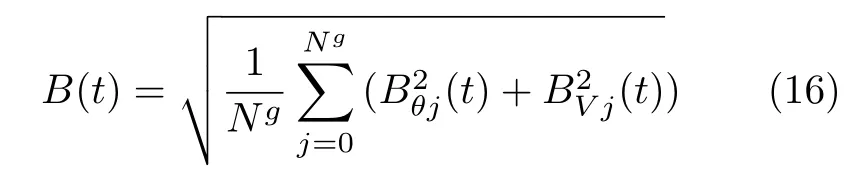
攻击者通过修改部分通信设备的量测值后,使得全局的状态估计结果和原始估计结果产生的均方根误差(RMSE)定义为攻击者的回报函数.

1.3 信息物理协同攻击模型

本节通过马尔科夫决策过程模拟恶意入侵者在动态环境中的攻击行为和电力信息物理系统的状态随时间演变过程.在遭受协同攻击后,电力信息物理系统在t时刻的系统状态与t −1 时刻的系统状态具有很高的纵向关联度.也就是说,在协同攻击下电力信息物理系统的状态演化过程具有马尔科夫性,因而本节建立基于马尔科夫决策过程的电力信息−物理双层协同攻击模型.

1.3.1 信息−物理脆弱性邻接矩阵

如图3 所示,定义电力信息−物理脆弱性邻接矩阵L:

图3 电力信息物理耦合网络Fig.3 The network of cyber-physical power coupling system

其中,脆弱性邻接矩阵的元素主要有4 类: 1)通信−通信节点连接矩阵Lc: 其中元素Lc,ij代表攻击者可以利用信息节点i上的漏洞,并进一步感染信息节点j.2)通信−物理节点连接矩阵Lf:Lf,ij表示母线i和j之间的传输线从控制中心向物理设备发送控制命令的过程.3) 物理−物理节点连接矩阵Lg:Lg,ij表示电力母线i和j之间的传输线.4)物理−信息节点连接矩阵表示信息节点i可以接收并传输物理设备j的相关量测值.当节点i和节点j之间存在传输线路时,Lij=1.相反,当节点i和j之间不存在传输线路时,Lij=0.

1.3.2 信息−物理双层耦合建模

如图4 所示,当前攻击者可模拟控制中心的功能,进行状态估计求得奖励回报值Reward,从而制定更精确更有效的攻击策略[6,34].由此,针对该类攻击者的攻击策略所制定的防御策略更具有研究意义.基于此,本节给出在上文所提出的信息物理协同攻击下跨空间渗透和反馈决策机理.首先,根据攻击策略π发动攻击行为Action,感染相关的通信层设备,使其从正常态S变为感染态I,并在通信网络中扩散;然后,感染态的信息节点将从PMU中收集到的量测值zg(t) 进行篡改,使其变为错误的量测值(t);随后,状态估计器使用错误的量测值估计出错误的状态量x(2)(t)+exz,计算状态量的误差,该误差值作为奖励回报值Reward 反馈给攻击者;最后,攻击者会根据相应的回报值调整接下来的攻击行为,通过不断地模拟,修正策略,最终得到使得目标函数最大的最优攻击策略.其中,感染态的信息节点对邻接的PMU 量测值注入虚假数据的函数为

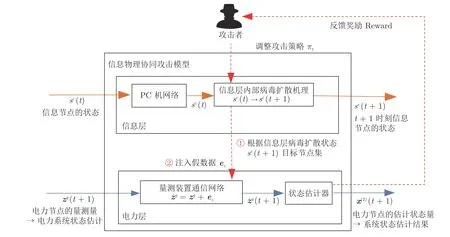
图4 信息物理协同攻击下跨空间渗透和反馈决策机理Fig.4 Cross-space penetration and feedback decision mechanism under cyber-physical collaborative attack

由于PMU 的采样频率很高,大约为30 次/s,而大多数研究表明攻击者攻击间隔 ∆t大约是秒级.为了解决注入假数据时刻和PMU 采样时刻并不一致的问题,本文采用基础的PMU 缓存的方法,即当攻击者在t时刻对PMU 量测量注入假数据时,直接选取PMU 缓存器中距离t时刻最近时刻的存储数据篡改.由此,这里根据攻击间隔对原本离散的PMU 采样值进一步离散化.

1.3.3 攻击者的目标函数

攻击者的最终目标为: 从初始状态在时间T内采取策略π后,能够获得期望的Reward 值达到最大.即对电力网络的破坏程度与对通信设备的利用成本的比值的累积和W达到最大,定义其最大值为

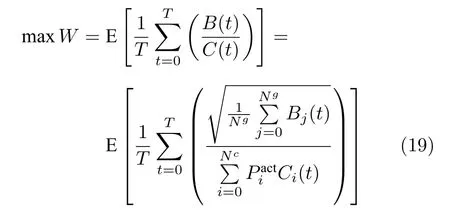
电力网络的约束条件为

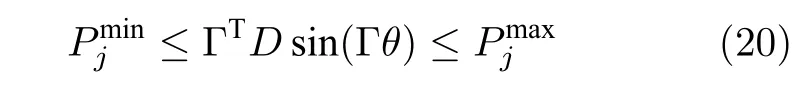
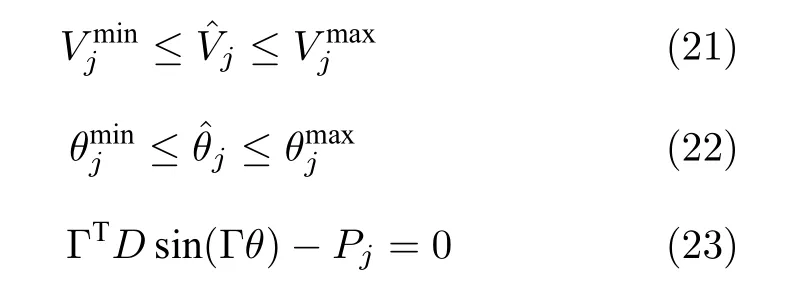
信息网络的约束条件为

其中,B(t)表示攻击者在时间t的攻击收益,由式(16)求得.C(t) 表示攻击者的攻击成本,定义为C=,其中Ci(t) 由式(8)求得.式(20)～(23)是关于电力系统的约束条件. Γ 是智能电网拓扑的关联矩阵,D是线路导纳的对角矩阵.此外,式(24)和式(25)是网络设备的限制.由于资源有限,在攻击持续时间 [ 1:T] 期间只能执行n次攻击动作,∥π∥0代表策略π的0 范数.攻击者发动某次攻击之后信息节点i的攻击概率为,其概率和为1.该目标函数同时考虑了电力系统和通信网络的耦合影响.

1.3.4 协同攻击建模

本节将通信−电力协同攻击建立成一个四元组(S,A,R,P)的马尔科夫决策过程.

1) 状态集合S={sI,sII,sIII: 表示马尔科夫模型中的状态集,其中任一状态s由Nc个通信设备的状态和Ng个物理设备的状态两部分组成,分别用sc和sg表示.sc表示通信设备的状态,该状态包括易感染态、感染态和恢复态,见式(1).

2) 动作集合A={aI,aII,aIII,···,aNA}: 表示攻击者能够采取攻击的动作集,针对每一个系统状态s均有响应的动作集φ(π(s)).攻击者的某次攻击动作a是对所有的通信设备的攻击概率分布,即

其中,不在扫描集ϕV(t) 中的通信设备的攻击概率为0.因为在t时刻攻击者无法直接或间接的扫描到该设备,所以并不能对该设备上的漏洞加以利用.在每个攻击时间,选择目标节点i进行攻击的概率为.

3)状态转移概率P: 从t时刻的状态s转换到t+1 时刻的状态s′需要经过一个过渡状态s˜,该状态表示该时间间隔内信息层设备的病毒扩散过程结束,但该攻击效果还没有渗透到物理设备.由式(18)可以得出s˜→s′时信息层发生状态改变后对物理层的渗透影响.处于状态s的系统采取动作a后状态转移到s′的概率定义为P(s′|s,a).P(s′|s,a) 包括两部分,分别是攻击行为a造成的通信层设备感染概率P(s˜|s,a)和电力层设备注入虚假数据后不能被检测概率P(s′|s˜).值得注意的是,这里s′仅与s˜ 有关,与a无关.

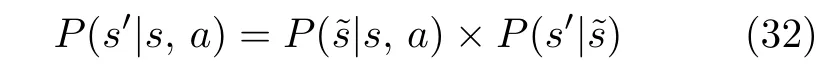
对受到攻击者攻击行为a之后的信息层设备状态转移概率和攻击者攻击概率求和,分别可由式(1)和式(32)求得

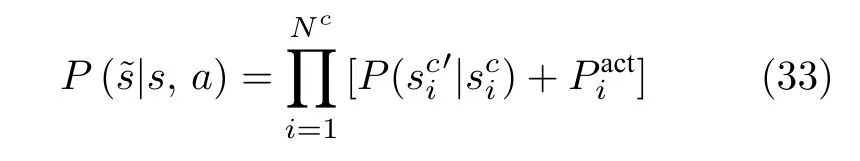
攻击者发动攻击后成功避开检测装置,即攻击行为在电力层成功渗透的概率为

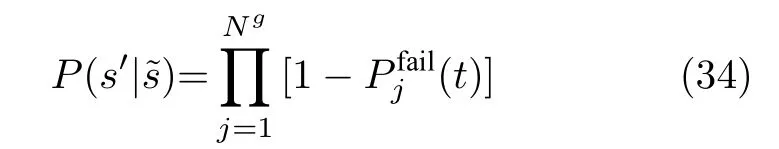
4)奖励回报值R(s,a): 表示系统在t时刻s状态时采取a行动后转移到t+1 时刻s′状态后整个[0,t+1] 时间段内的预期奖励回报.其定义为这段期间内攻击者的攻击成本与攻击收益的比值累积和,即

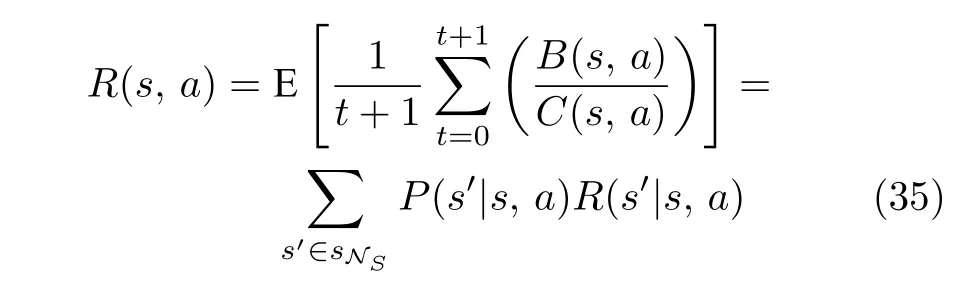
2 基于Q-learning 的模型求解

本文使用Q 学习求解所提的协同攻击模型下的最优攻击策略.首先采用Q-learning 的方法根据攻击者目标函数求得最优策略.目标函数可由式(19)求得.最后分析在该最优攻击策略下各个电力设备被攻击的可能性,由此可以识别电力系统的薄弱节点.

2.1 Q-learning 求解过程

基于Q-learning 的攻击者最优攻击路径求解的基本思路为: 攻击者根据Reward 奖励值反馈或惩罚刺激下,逐步修正自己的攻击策略π,最终求解在有限攻击资源下最大化预期总奖励的最优攻击策略,即

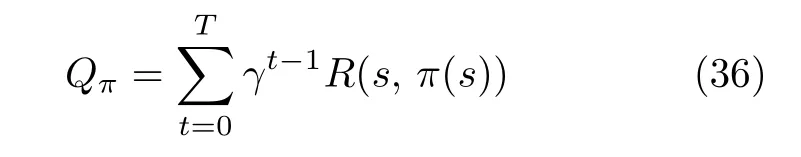
其中,γ为折算因子,γ∈[0,1).由于信息网络路由选择概率和网络延迟等原因,其中求解R(s,π(s))所需要的P(s˜|s,a) 不能直接求得,见式(32).所以本文使用NS2 软件通过蒙特卡洛方法模拟大量的信息网络状态过程求得.接下来,在s下最优攻击策略π∗可以通过下式计算:

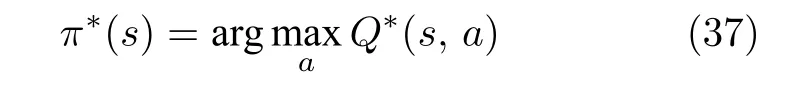
为了避免局部最优的出现,许多随机动作序列将被搜索以更新Q 表,在此期间,攻击者动作序列最终会被修改为最佳攻击策略,即

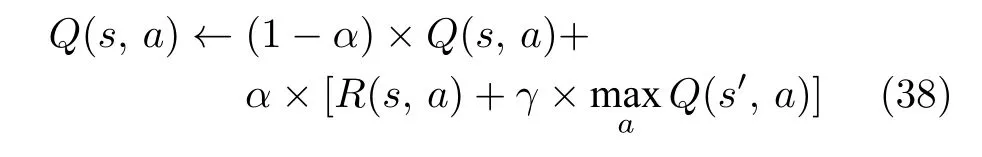
其中,α是学习速率.最终,该最优攻击策略相当于攻击者的一个预判行为,通过该预判行为可以分析哪些电力元件成为攻击者攻击目标的可能性更大,能够对防御资源的分配起到指导作用.

在制定状态−动作Q 矩阵时,由于变量之间存在关联关系,所以许多系统状态在整个探索过程中均未出现.如果使用传统的Q 矩阵,随着变量的增加,状态集和动作集均会呈指数增长,最终导致运算速率过慢.因此,本文将传统的静态稀疏Q 矩阵转换为动态更新的满秩Q 矩阵,以加快运算速率并节约存储空间.

2.2 电力元件被攻击的可能性分析

在求得最优策略下,根据各个电力设备被攻击的可能性,研究相应节点的特性,并指导相关的防御行为.因为马尔科夫决策过程的状态转移概率存在随机性,所以攻击者采取相同的攻击策略时,导致电力信息物理系统的破坏程度也存在随机性[19].基于此,首先定义在马尔科夫决策过程中系统状态为sX时,状态分布概率为

3 算例分析

3.1 仿真模型与参数设置

如图5 所示,本模型在一个通信8 节点−电力IEEE14 节点的耦合系统上进行测试,该算例系统由两部分组成,上层通信层由8 个通信设备C-n 组成,下层电力层是IEEE14 节点系统,该通信网络服务于电力系统的状态估计功能.当攻击者发动远程网络攻击时,病毒在通信网络节点之间以蠕虫形式传播,将虚假数据注入通信设备.在该算例系统中,通信网络使用NS2 软件仿真,该软件可以考虑更多实际情况,如链路阻塞、丢包等过程,仿真结果更加准确.该算例系统在参数设置时采用UDP 协议和自带的单播路由协议,并选择具有代表性的已经公开的PLC 机上的漏洞,相关的通信网络参数见附录A,其中移除率和恢复率分别为0.001和0.01(参见文献[4]).为了使实验结果更直观,做出以下假设:

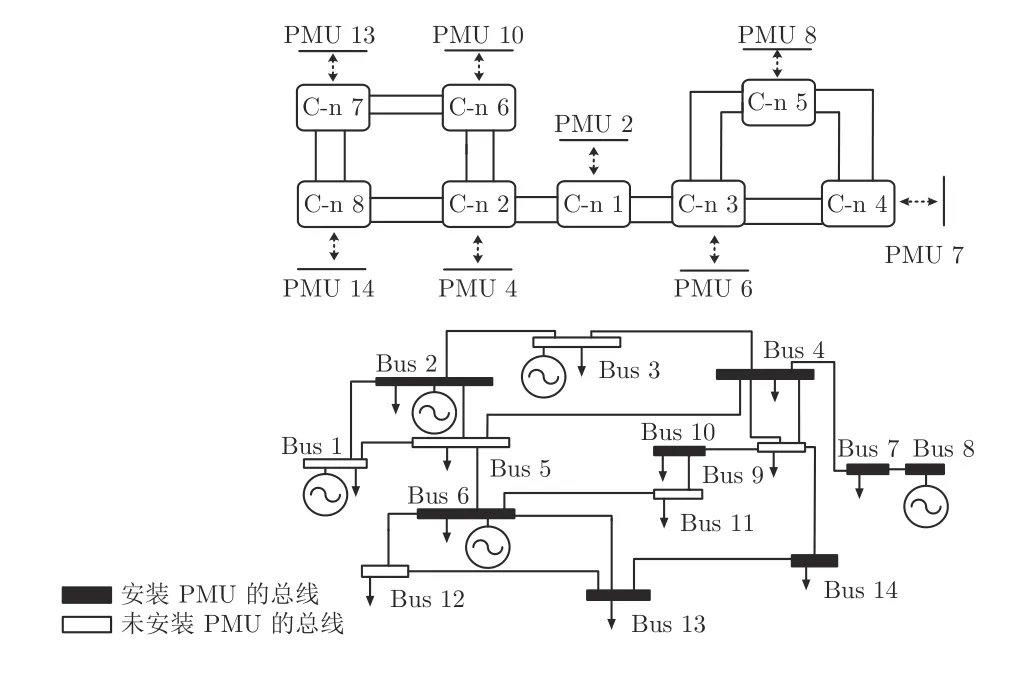
图5 通信8 节点−电力IEEE14 节点耦合系统Fig.5 Cyber 8-Power IEEE14 node coupling system

假设 1.攻击者动作集合均采用单层攻击目标的动作,即攻击目标为i时,

假设 2.电力节点和信息节点是一一对应的,电压量测值允许的偏差为±5%,单次修改的虚假数据为原始量测值的±1%.

Q-learning 算法的每一个训练周期都是从攻击者发动攻击开始.在算例系统上进行15 000 次仿真训练,每次训练都设置的时间间隔为T=3∆t,其中攻击间隔取值 ∆t=1 s[19].其目标是寻找最优攻击策略,以获得最大的积累回报值.图6(a)显示了每次训练中采用不同的攻击策略的累积奖励.整个搜索的过程可分为3 个部分: 起始状况、局部最优和全局最优.截止到886 次测试时,攻击者累积奖励没有显著增加,保持其初始值为1.783.从887 次训练开始,积累奖励值从1.783 迅速增加到2.156,即找到了局部最优解.然后在3 962 次训练时,累积奖励从2.156 急剧增加到2.242,即找到全局最优解.3 963次训练之后,奖励值保持稳定并且仍然是最大值,这意味着确定了最优攻击策略.同时,随着训练次数的增加,图6(b)显示经过大量训练之后Q 值趋于恒定,这表明已经搜索到最优的攻击策略.

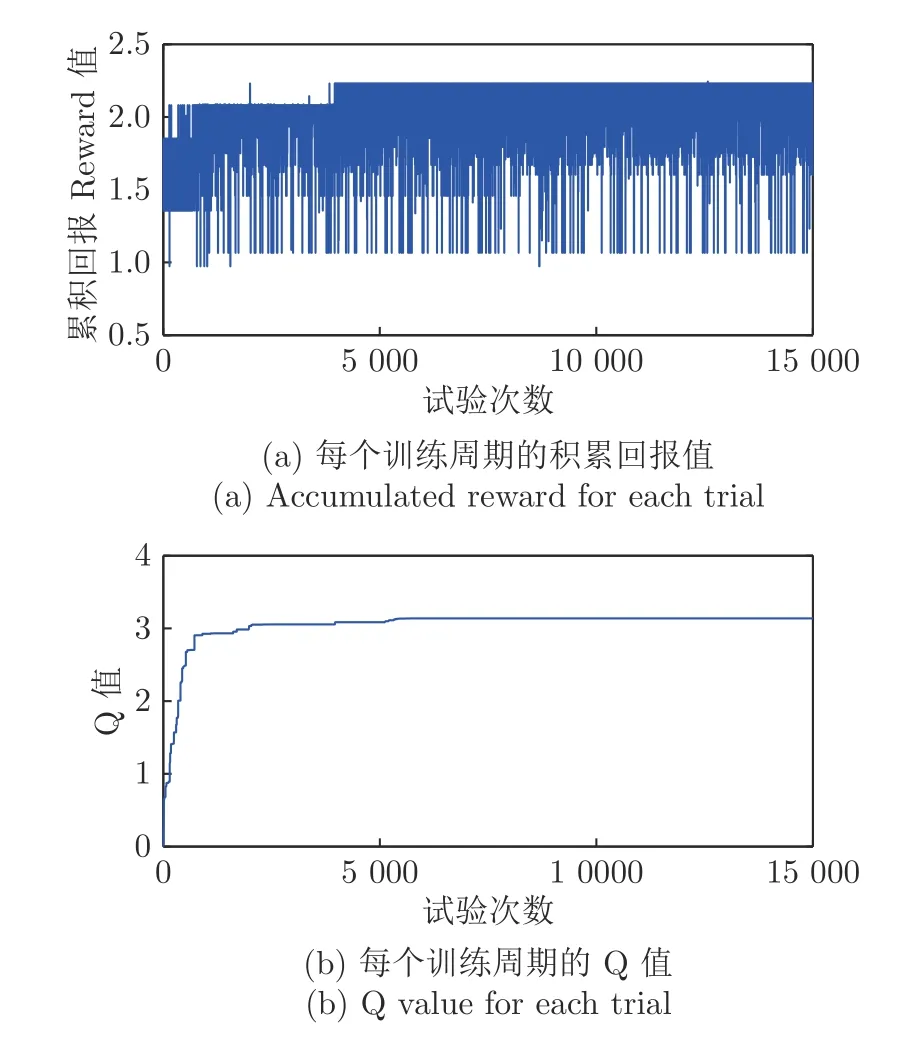
图6 每个训练周期的累积收益Fig.6 Accumulated benefit for each trial

在本节的算例仿真中,攻击者最优策略下的攻击序列为C-n 4→C-n 2→C-n 1,映射到电力系统中为Bus 7→Bus 4→Bus 2,每一次攻击行为之后蠕虫病毒在通信网络的扩散情况如图7 所示.

图7 最优攻击策略下攻击者的攻击序列和病毒扩散序列Fig.7 The attack sequence and virus spreading sequence under the optimal attack strategy

图8 横坐标从左到右分别是初始状况、攻击者第1 次攻击动作后、第2 次攻击动作后和第3 次攻击动作后.纵坐标表示在最优的攻击策略下估计状态值偏差的百分比,即式(16)的值.

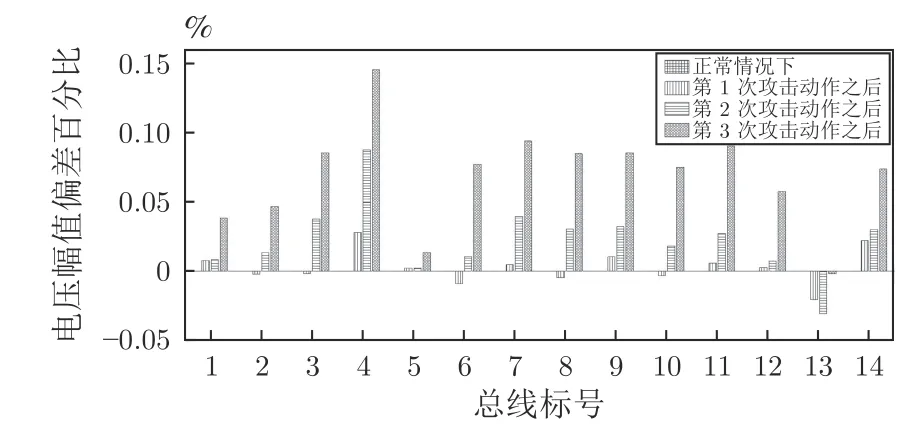
图8 在最优攻击策略下电压幅值差百分比Fig.8 Difference percentage in voltage amplitude under optimal attack strategy

可以推断,如果只修改一个母线的测量值,则可能由检测机制检测并且能够被校正;如果攻击者同时修改某条母线及其相邻母线的测量值,就会使估计器无法检测到错误数据,从而使估计误差变大.在该算例中电力母线4 受到攻击的可能性最大,是系统中较为薄弱的环节,在防御者进行资源分配的时候应该优先考虑.

3.2 结果分析

为了验证本文提出的协同攻击具有更好的攻击效果,这里对网络攻击、物理攻击和信息物理协同攻击3种不同攻击方法的攻击效果进行仿真实验,对比结果如表1 所示.其中,n表示发动攻击的次数.网络攻击指的是攻击者的目标是只考虑信息层攻击成本最小,不考虑电力系统的破坏程度;物理攻击指的是传统的电力系统攻击研究,即假设在通信层量测设备能够无差别地被攻击者篡改的条件下,攻击者目标是对电力系统破坏程度最大.

从表1 可以看出,协同攻击在3种攻击方法中表现最好,物理攻击次之,网络攻击最差.其中,π∗表示当前攻击者的最优攻击策略,exz表示估计状态值的误差,f(∆V) 表示电压幅值偏差百分比的累积量,f(∆θ) 表示电压相位角的偏差百分比的累积量.需要注意的是,当攻击者采用网络攻击时,每个物理节点的攻击回报值设置为1.随着攻击时间的增加,协同攻击的有效性变得更加显著.由此可见,当攻击者只考虑利用信息节点漏洞的利用能力时,虽然受感染的网络节点数量在短时间内增加,但对电力网络的影响很小.此外,单纯的物理攻击可能效果不佳,这是因为与某些关键电力节点相连接的通信网络节点在通信层难以得到利用.

表1 考虑不同攻击方法下的影响Table 1 Attack effect under different attack methods

表2 对比了在协同攻击和物理攻击下各个电力设备被攻击的可能性,概率和为1.由分析可知,当考虑到通信层设备的影响时,与在通信网络中更脆弱的信息设备相连接的电力设备的脆弱性显著增加,且边缘信息设备的脆弱性与该设备在通信网络中连接度的大小和元件上存在的漏洞的利用难易程度相关.例如: 采用物理攻击时,母线10 的脆弱性最高,因为连接母线10和母线9 的电力线具有比其他支路更小的电抗.当虚假数据注入母线10 的测量值时,状态估计器的估计结果将具有更大的误差.当采用协同攻击时,母线2 (对应通信设备1)的量测值被篡改的概率急剧增加.主要有两个原因:1)母线2 是电力网络中较为关键的节点;2)通信设备C-n 1 在通信网络中具有较大的连接度,当其被成功感染时,其相邻网络设备C-n 2和C-n 3 的攻击概率将显著增加.随着时间的推进,与C-n 2和C-n 3邻接的通信设备将陆续被感染,从而扩散到整个通信网络.

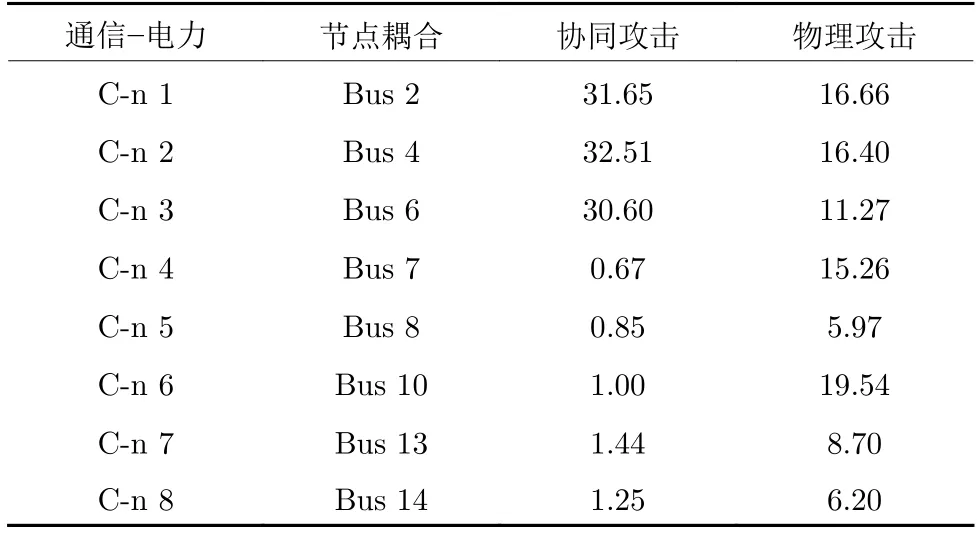
表2 电力设备被攻击可能性分析(%)Table 2 The vulnerability analysis of power equipment (%)

3.3 不同参数对攻击效果的影响

本节讨论系统的离散程度和注入虚假数据的正负是否对协同攻击效果有影响.

3.3.1 系统离散程度对攻击结果的影响

对于算例系统,当各个母线的电压幅度和角度的离散状态的数目和的值在4～8 的范围内发生变化时攻击效果如表3 所示.

由表3 推断,当系统状态离散情况发生变化时,算例系统中每条母线的脆弱性几乎没有变化.

表3 系统离散程度不同时电力设备被攻击的可能性分析Table 3 The vulnerability analysis of power equipment under different discrete degrees of false data

3.3.2 注入虚假数据的正负对攻击结果的影响

对于算例系统,当ez=[eθ,eV]T的数值取正值、负值或者混合符号数据时,攻击效果如图9 所示.

由图9 推断,注入的假数据的符号不同对算例系统中每条物理母线脆弱性影响不大.

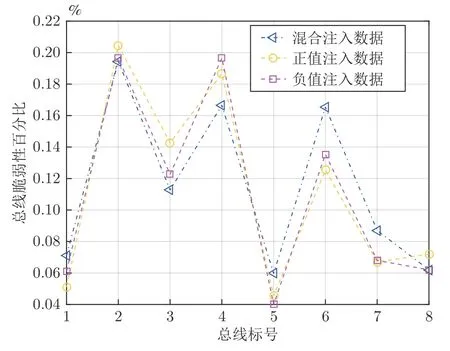
图9 注入虚假数据取不同符号下电力设备被攻击的可能性分析Fig.9 The vulnerability analysis of power equipment under different signs of false data

4 结束语

本文从攻击者角度出发,提出了一种电力信息物理协同攻击模型,该模型同时考虑通信层设备的攻击难易程度以及对电力物理系统的破坏程度两方面因素.然后,本文结合通信层和电力层设备的特性,制定攻击成本和攻击收益函数,并定义攻击收益与成本的比值为目标函数.随后,采用Q-learning 求解所提模型下的目标函数最大的最优攻击策略.最后,利用通信8 节点−电力IEEE14 节点联合仿真算例对单层网络攻击、物理攻击和协同攻击方式的攻击效果进行对比,并分析了元件被攻击的可能性,得到的结论如下: 1)本文所提出的信息物理双层协同攻击模型可以准确地描述攻击行为在电力信息物理系统中的动态攻击效果和级联影响;2)通过算例研究,验证了相较网络攻击和物理攻击,本文所提的协同攻击由于同时考虑通信层设备的利用难度和电力设备的破坏程度两方面因素的耦合影响,所以攻击效果更好,物理攻击次之,网络攻击效果最差;3)由仿真结果分析可得,由于电力信息物理系统的通信层和电力层设备存在复杂的耦合关系和交互机理,所以通信层元件利用的难易程度和通信网络结构对电力设备潜在被攻击的可能性存在显著影响.

附录A

表A1 NS2 中通信网络的参数配置Table A1 The parameters of cyber network in NS2

表A2 每个通信设备上存在的漏洞的CVSS 评分Table A2 The CVSS standards of each cyber node