具有间歇性执行器故障的非线性系统自适应CFB 控制

乃永强 杨清宇 周文兴, 杨莹

由于故障时刻,故障模式以及故障值完全不可预测,因此如何消除执行器故障对控制系统的影响已成为控制领域的技术难点[1].到目前为止,自适应控制[2−3]已成为解决执行器故障补偿问题的有效策略.与其他控制方法相比,自适应补偿控制具有如下的优点: 1) 能够自动调节执行器故障引起的不确定性;2) 控制器利用自适应律可在线调整其估计参数;3) 当故障信息完全未知时,也可以获得期望的控制目标.利用线性矩阵不等式技术,文献[4−6]分别研究了线性系统执行器故障的自适应补偿问题.文献[7]提出的直接自适应控制方案解决了具有卡死 (Lock in place,LIP) 执行器故障和未知系统参数的线性系统的跟踪控制问题.结合自适应Backstepping 控制技术,文献[8−10]分别研究了具有LIP 故障的非线性系统的补偿控制问题.文献[11−12]解决了具有部分失效 (Partial loss of effectiveness,PLOE)和LIP 故障的非线性系统的跟踪控制问题.文献[13]解决了具有 PLOE 故障和LIP 故障以及松浮 (Float) 故障的非线性系统的跟踪控制问题.由于NNs (Neural networks)或模糊逻辑系统的通用逼近特性,文献[14−19]提出的自适应神经或模糊控制方案补偿了执行器故障对系统的影响.然而,文献[4−19]仅仅解决了一次性执行器故障的补偿问题,即所有执行器的状态在故障发生之后保持不变.虽然在故障时刻存在未知参数的跳变,但未知参数的跳变次数和Lyapunov 函数有界,因此可以保证闭环系统的稳定性和期望的跟踪指标.

在实际应用中,控制系统的执行器在运行过程中也经常发生各种不可预测的间歇性故障.即执行器的状态在正常运行和故障之间（或者各种故障之间）进行频繁地切换.正如文献[20]所指出的,间歇性执行器故障会不可避免地导致系统中未知参数的间歇性跳变,并且跳变的总次数可趋于无穷大.因此,一次性故障的研究成果[4−19]不能直接用于具有间歇性执行器故障的控制系统的补偿控制中,主要有如下的原因: 1) 随着跳变次数的不断累积,控制器中的一些估计参数会不断的增加,最终当跳变次数趋于无穷大时,这些估计参数将变得无界;2) 由于存在未知参数的间歇性跳变,则包含参数估计误差的 Lyapunov 函数在每个跳变时刻必将产生一个跳变幅度.从而上述 Lyapunov 函数的可能增加随着跳变次数的增加而不断累积,最终当跳变次数趋于无穷大时,闭环系统的稳定性将得不到保证.因此,在间歇性执行器故障的自适应补偿控制方案设计中,如何有效地保证参数估计的有界性以及闭环系统的稳定性是执行器故障补偿领域的一个技术难点.

目前关于非线性系统的间歇性执行器故障补偿控制的研究成果还非常有限.在文献[20]中,Wang等首次解决了一类参数化严格反馈非线性系统的间歇性执行器故障的补偿问题.所设计的自适应模块化控制方案保证了所有闭环信号的有界性.但是,该方案仅仅保证了均方意义上的跟踪误差的有界性.从而不能建立跟踪误差与设计参数之间的明确关系.受文献[20]的启发,Lai等[21−22]和Xing等[23]进一步研究了非线性系统间歇性执行器故障的补偿问题.文献[24]解决了含有未知时滞非线性系统的间歇性执行器故障的补偿问题.文献[25]解决了航天器姿态控制系统间歇性执行器故障的补偿问题.采用K−滤波器技术[26−27],两种自适应输出反馈控制方案补偿了间歇性执行器故障的影响[28−29].但是,以上方案[20−25, 28−29]仅仅证明了系统的稳定性和稳态跟踪指标,没有建立跟踪误差意义下的系统暂态指标与设计参数之间的关系.从而不能通过调节设计参数改善系统的暂态指标.在文献[22]中,作者在假设故障次数有限的前提下,提出了一种暂态跟踪误差指标的显式界.但是该界取决于系统中故障的次数.当故障次数趋于无穷大时,系统的暂态指标不能被保证.则文献[22]中建立的系统暂态指标不能应用于考虑无限次故障的暂态指标分析中.因此,在间歇性执行器故障的情况下,所设计的补偿控制方案中如何明确地建立跟踪误差意义下的系统暂态指标与设计参数之间的关系并通过调节设计参数获得良好的系统暂态指标也具有重要的理论与工程意义.

此外,文献[9−13,20−23,28−29]设计的基于传统的 Backstepping 故障补偿控制方案需要对虚拟控制律的偏导数进行解析计算.如文献[30−31]所述,随着系统阶数的增加,上述计算将变得非常复杂,从而限制了上述方案在实际中的应用.鉴于此,文献[30−31]提出的CFB 控制技术在不满足匹配条件的非线性系统的自适应控制中引起了广泛的关注.与传统的Backstepping 技术相比,CFB 方法有如下的优点: 1) 指令滤波器可精确地估计虚拟控制信号及其导数;2) 消除了虚拟控制律解析微分的计算,使得控制律的设计更容易实现;3) 指令滤波器引起的滤波误差在控制器中得到了补偿.因此,本文采用 CFB 控制技术,针对一类不确定严格反馈非线性系统,提出一种自适应控制方案以解决间歇性执行器故障的补偿问题.

本文的主要贡献如下:

1) 采用投影算子在线调整控制器中的估计参数,可消除故障次数不断累积而导致的估计参数值不断增加的问题.

2) 改进的Lyapunov 函数证明了所提出的方案能够保证所有闭环信号的有界性.同时明确地建立了跟踪误差与Lyapunov 函数的跳变幅度,最小故障时间间隔和设计参数之间的关系.特别是,Lyapunov 函数的跳变幅度越小和两个连续故障之间的时间间隔越长,系统跟踪指标越好.应该指出的是,系统的跟踪指标与故障次数无任何关系.

3) 通过迭代计算建立了暂态跟踪误差指标的均方根型界.该界说明了通过选择恰当的设计参数,可获得良好的跟踪误差意义下的系统暂态指标.需要说明的是,该均方根型界不依赖于故障的总次数.

本文其余部分安排如下: 第 1 节给出了问题的描述.第 2 节设计了控制方案.第 3 节进行了仿真研究.第 4 节总结了全文并给出了进一步的研究工作.

1 问题描述

1.1 非线性系统

考虑如下不确定严格反馈非线性系统

2) 便于第 2 节的控制器设计以及稳定性分析,给出如下的定义.在时间区间 [tq,tq+1) (q∈N+)内,假定有mq(mq ≤m −1) 个执行器k1,···,kmq发生 LIP 故障,且在未知时刻tq+1之前,所有执行器的状态不发生变化.

控制的目标是设计一种自适应控制方案使得:a) 能够有效地补偿未知间歇性执性行器故障对系统的影响;b) 闭环系统中所有信号的有界性被保证;c) 系统的输出y∈R 可跟踪期望输出yd∈R,其中yd和y˙d已知且有界;4) 通过选择恰当的设计参数,可调节系统在跟踪误差意义下的稳态和暂态指标.

为了实现上述控制目标,需要如下的假设.

假设 1.在每个时间间隔 [tq,tq+1) 内,当任意不大于m −1 个执行器发生LIP 故障时,剩余的执行器仍可驱动系统完成上述控制目标.

注 2.假设 1 是保证系统 (1) 可控性的基本且必要的假设.在每个时间间隔 [tq,tq+1) 内允许所有执行器同时发生 PLOE 故障.但是当所有执行器同时发生 LIP 故障时,则不能完成上述控制目标.假设 1 还表明了每个执行器存在无限次故障的可能性.假设 2[30]表明了非线性函数fi(·),gi(·),bk(·)在x∈Rn上满足 Lipschitz 条件.因此,对于任意的x(0)∈Rn,系统 (1) 都存在唯一的连续解x(t)[32].从而系统 (1) 定义的初值问题的解x(t) 的有界性在∀t∈[0,∞) 上被保证.假设 3 表明了故障参数的 有界性以及上的变化率的有界性.已知常数和将用于第2.2节的自适应律设计中.此外,假设和上均为光滑函数仅仅是为了第 2.3 节的稳定性分析的目的,不用于控制器的设计中.

1.2 极限学习机的学习理论

极限学习机 (Extreme learning machine,ELM) 是由 Huang等[33]提出的用于单隐层前馈NNs 的快速学习算法,其本质上是一种单隐层前馈NNs.ELM 特点是随机选择网络隐含层节点参数,在学习过程中仅需要调节网络的输出权值.正如文献[34]所指出的,ELM 不仅提高了单隐层前馈NNs 的学习效率,而且完全保留了传统单隐层前馈NNs 固有的通用逼近能力.根据文献[34]中的定理II.1,对于任意的随机函数序列,ELM可以逼近任意连续函数f(Z):Rn →R:

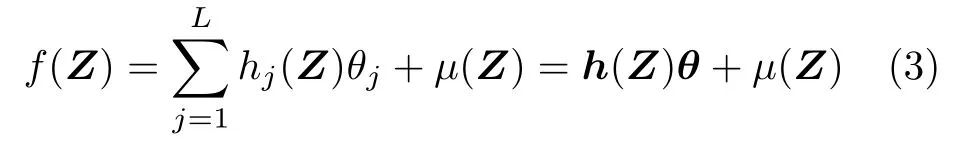
其中,Z∈SZ且SZ∈Rn表示紧集合;µ(Z) 表示逼近误差并且存在未知常数0,使得|µ(Z);激活函数hj(Z) 可表示为

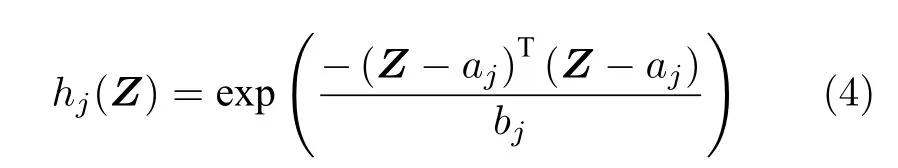
其中,j=1,···,L以及 (aj,bj) 表示第j个隐层节点的学习参数,其在 Rn×R+的任意区间上随机选择;θ=[θ1,···,θL]T∈RL表示 ELM 的最优权值,其真实值未知.因此,在第 2.1 节的控制器设计中,采用了基于估计的逼近模型

使得对于∀Z∈SZ,逼近误差µ最小.紧集合定义为

2 自适应神经补偿控制设计

首先,针对具有间歇性执行器故障 (2) 的系统(1),设计一种自适应 CFB 补偿控制方案,并采用投影算子实时在线更新控制器中的估计参数使得参数估计的有界性被保证.图1 给出了该控制方案的控制流程.在图1 中,以i=3 为例,α2表示指令滤波器 (11) 的输入,xc3和表示指令滤波器 (11)的输出,也表示虚拟控制律α2及其导数的估计,信号α2,xc3,ξ3通过积分运算生成指令滤波误差补偿信号ξ2.其次,考虑到未知故障参数的间歇性跳变对系统稳定性的影响,定理 1 提出一种改进的Lyapunov 函数分析了闭环系统的稳定性.证明了所提出的补偿控制方案能够保证所有闭环信号的有界性.同时明确地建立了跟踪误差与Lyapunov 函数跳变幅度,最小故障时间间隔,设计参数之间的关系.最后,定理 2 利用迭代计算建立了暂态跟踪误差指标的均方根型界,该界表明了通过选择恰当的设计参数,可获得良好的跟踪误差意义下的系统暂态指标.

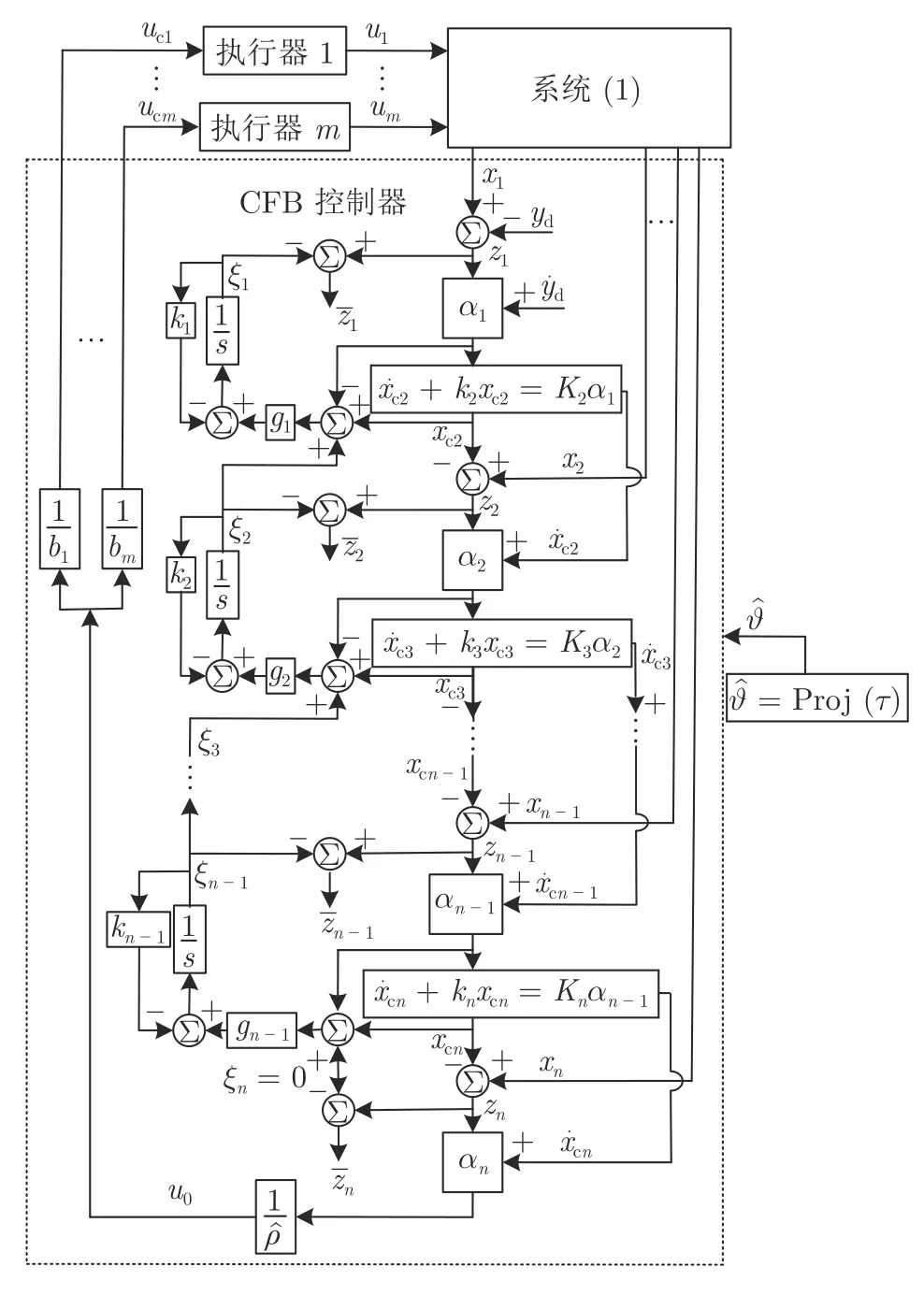
图1 控制结构图 (xci和 ,i =2,···,n,为滤波器(11) 的输出.αi ,i =1,···,n,为式 (12)～(14) 中定义的虚拟控制律.ξi ,i =1,···,n −1 为式 (17) 中定义的滤波误差补偿信号)Fig.1 Control block diagram (xci and fori=2,···,n are the outputs of the filter (11).αi fori=1,···,n is virtual control law defined in (12)～(14).ξi fori =1,···,n −1 is the compensating signal of the filtered error defined in (17))

2.1 故障补偿控制器设计

实际控制律设计为

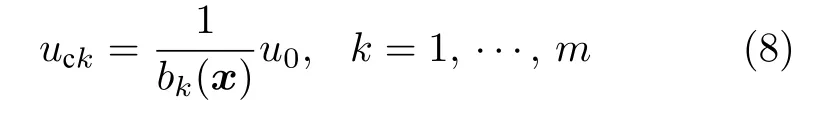
其中,u0将采用CFB 控制技术进行设计.利用注2 中的 2),并将式 (2)和式 (8) 代入系统 (1) 的第n个方程,有

其中,xc1=yd且yd为期望轨迹.由图1 可知,当i=2,···,n时,xci与其时间导数由如下的指令滤波器[30−31]生成

2.2 自适应律设计

根据假设1,有如下的结论:

注 4.引理1 表明了对于∀t∈[0,∞),投影算子(23)可明确地保证估计参数的有界性.从而消除了故障次数不断累积而导致的控制器中估计参数不断增加的问题.由于,∀t∈[0,∞),则有如下的结论: 1)保证了参数估计误差的有界性;2) 保证了由未知参数ϑ间歇性跳变引起的所有Lyapunov 函数的跳变幅度的有界性.结论1)和2)将应用于定理1 的证明中.

2.3 稳定性分析

闭环系统的稳定性分析由定理1 给出.

定理 1.考虑由具有间歇性执行器故障 (2) 的不确定严格反馈非线性系统 (1),实际控制律 (8)和(15),虚拟控制律 (12)～(14),滤波器 (11)和(17) 以及基于投影算子的参数自适应律 (19) 组成的闭环系统.令系统的所有初始条件均有界并满足假设 1～3 以及选择恰当的设计参数.即使在运行过程中存在未知参数的间歇性跳变,所提出的控制方案能够保证闭环系统所有信号的有界性.

证明.在每个时间间隔 [tq,tq+1) 内,Lyapunov 函数选择为

2.4 暂态指标分析

3 仿真研究

选择4 个实例为被控对象分别进行仿真实验,以验证所设计的自适应补偿控制方案对间歇性执行器故障的补偿能力和跟踪控制指标.

3.1 实验1: 数值仿真1

考虑如下的三阶严格反馈非线性系统

其中,j=1,3,···;T∗=20 s.从式 (44)和式 (45)中可看出,在每个jT∗s 时间段内,系统中第1 个执行器的输出将损失其有效性的 40%～80%,而第2 个执行器将锁死在u2=8+4 cos(8t).在其余时间段内,两个执行器均运行在无故障情况下.

首先,从图2 (a) 可看出,系统的输出y可跟踪给定的期望输出yd.从图2 (b) 可看出,跟踪误差可渐近地收敛到零的一个很小的领域内,并且增加控制增益参数k1,k2,k3和自适应律因子Γ可获得很小的跟踪误差.其次,图3～5 分别表明了控制输入信号u1,u2,滤波信号xc2,xc3,ξ1,ξ2和估计参数的有界性.从图5(c)～5(f) 中可清楚地看出,动态参数随着执行器状态的不断切换而不断跳变.但是,选择投影算子实时在线更新控制器中的估计参数,使得的有界性可得到明确地保证.最后,从图2～5 中可看出,在均匀间隔周期执行器故障的情况下,所提出的补偿控制器能够驱动系统完成预期的跟踪控制指标,同时保证了闭环系统中所有信号的有界性.

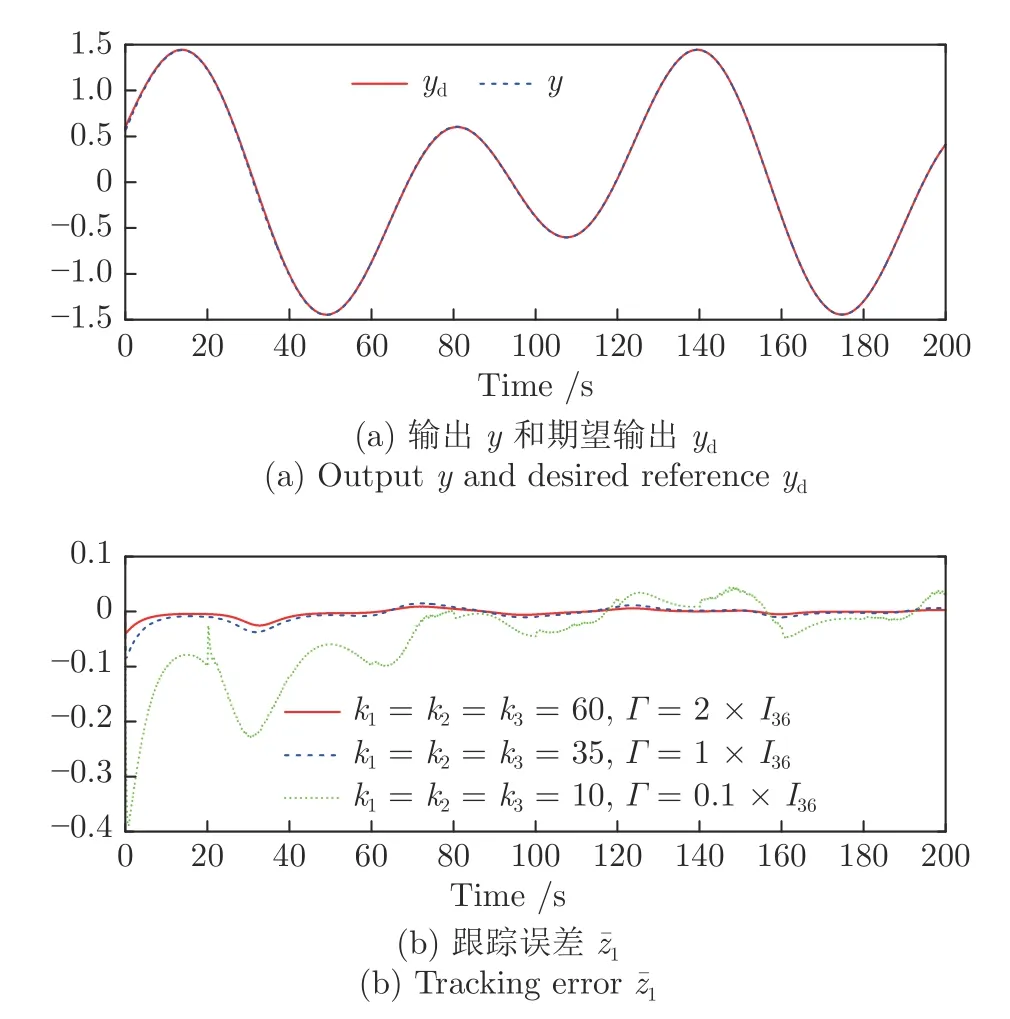
图2 实验1 中输出y,期望轨迹yd 及跟踪误差Fig.2 Outputy,desired trajectoryyd and tracking error in Experiment 1

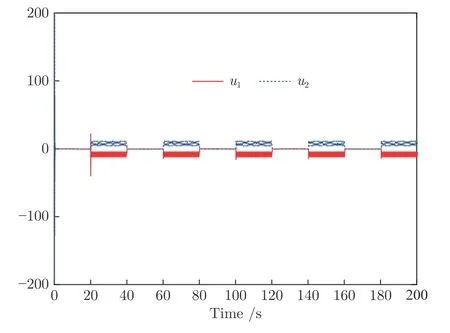
图3 实验1 中控制输入u1和u2Fig.3 Control inputsu1 andu2 in Experiment 1

图4 实验1 中命令滤波误差及其补偿信号Fig.4 Command filtered errors and their compensating signals in Experiment 1

图5 实验1 中自适应参数Fig.5 Adaptive parameter in Experiment 1

3.2 实验2: 数值仿真2

选择如下的三阶不确定严格反馈非线性系统

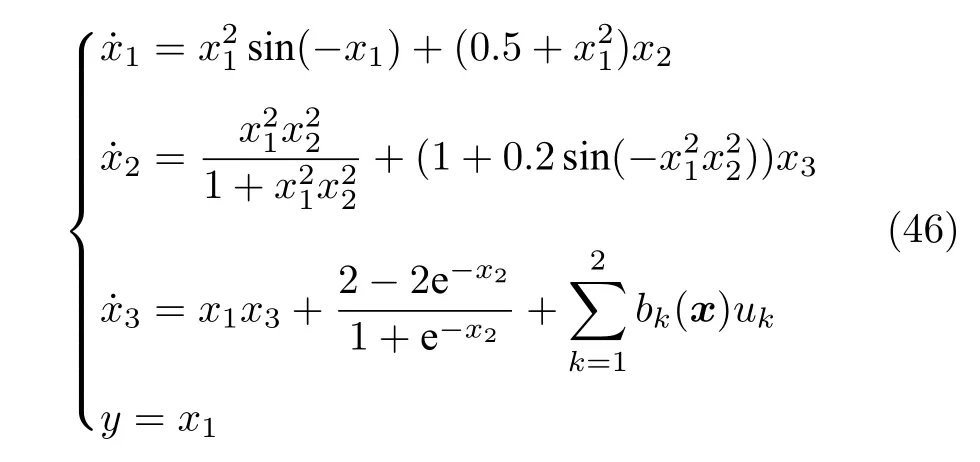
其中,b1(x)=b2(x)=2+sin(x1x2x3).

执行器故障模型选择为

首先,图6(a) 表明了系统的输出y可跟踪给定的期望输出yd.图6(b) 表明了跟踪误差可渐近地收敛到零的一个很小的领域内,并且增加控制增益参数k1,k2,k3和自适应律因子Γ可获得很小的跟踪误差.其次,图7～9 分别表明了控制输入信号u1,u2,滤波信号xc2,xc3,ξ1,ξ2和估计参数的有界性.从图9(c),9(e)和9(f) 中可清楚地看出,动态参数随着故障参数跳变次数的增加而不断跳变.但是,基于投影算子的参数自适应律可以保证的有界性.最后,从图6～9 中可看出,在非均匀间隔周期执行器故障的情况下,所提出的自适应补偿控制器不仅成功地驱动系统完成预期的跟踪控制指标,而且保证了所有闭环信号的有界性.

图6 实验2 中输出y,期望轨迹yd 及跟踪误差Fig.6 Outputy,desired trajectoryyd and tracking error in Experiment 2

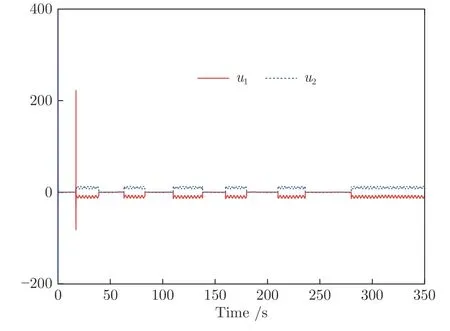
图7 实验2 中控制输入u1和u2Fig.7 Control inputsu1 andu2 in Experiment 2

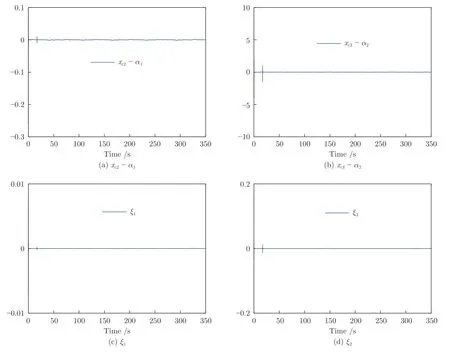
图8 实验2 中命令滤波误差及其补偿信号Fig.8 Command filtered errors and their compensating signals in Experiment 2

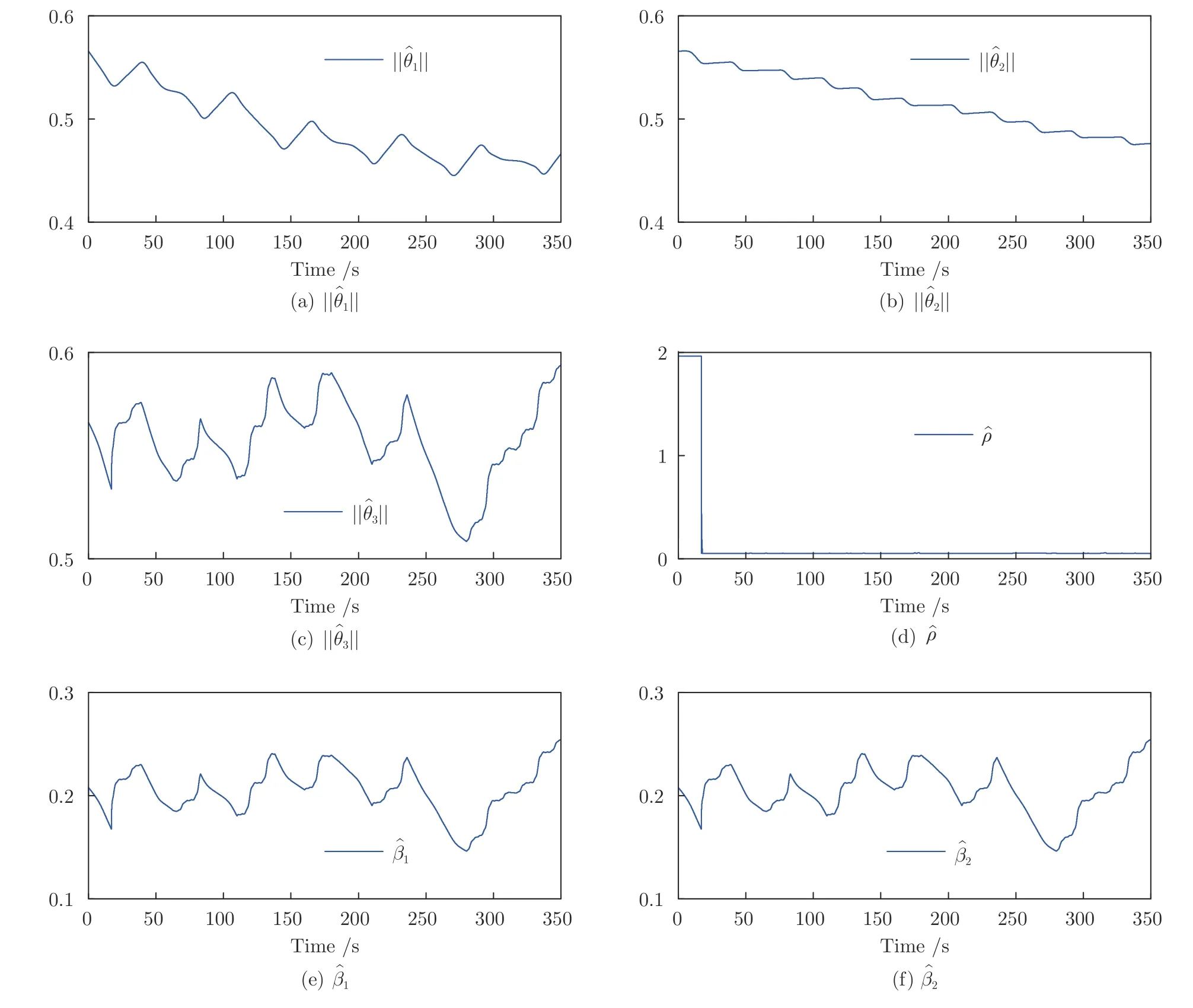
图9 实验2 中自适应参数Fig.9 Adaptive parameters in Experiment 2

3.3 实验3: 三阶单关节机器人的控制应用

将所提出的控制方案应用于实际的三阶单关节机器人控制系统[36]中,以验证其对间歇性执行器故障的补偿能力.三阶单关节机器人的动态方程为

其中,b1=b2=1/M. 在仿真中,系统参数选择为D=B=1,M=0.05,Km=10,J=0.5和N=10.

执行器故障模型选择为

其中,j=1,3,···;T=15.从式 (51)和式 (52) 中可看出,在每个jT∗s 时间段内,系统中第1 个执行器将锁死在 6 +2 cos(3t),而第2 个执行器的输出将损失其有效性的 20%～80%,在其余的时间段内,两个执行器均运行在无故障情况下.

3.4 实验4: 柔性机器人的控制应用

将所提出的控制方案应用于实际的柔性机器人控制系统[36]中,以验证其对间歇性执行器故障的补偿能力.柔性机器人的动态方程可表示为

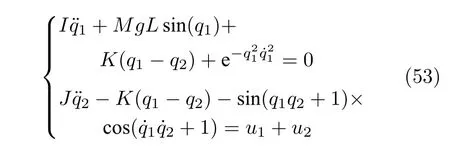
图10 实验3 中输出y,期望轨迹yd 及跟踪误差Fig.10 Outputy,desired trajectoryyd and tracking error in Experiment 3

图11 实验3 中控制输入u1和u2Fig.11 Control inputsu1 andu2 in Experiment 3

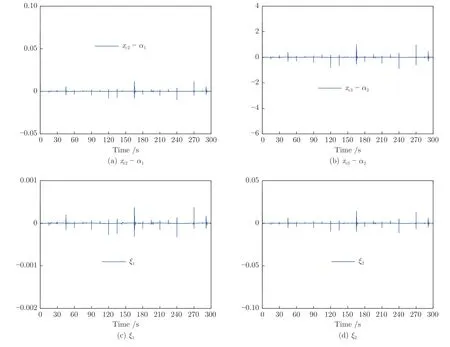
图12 实验3 中命令滤波误差及其补偿信号Fig.12 Command filtered errors and their compensating signals in Experiment 3

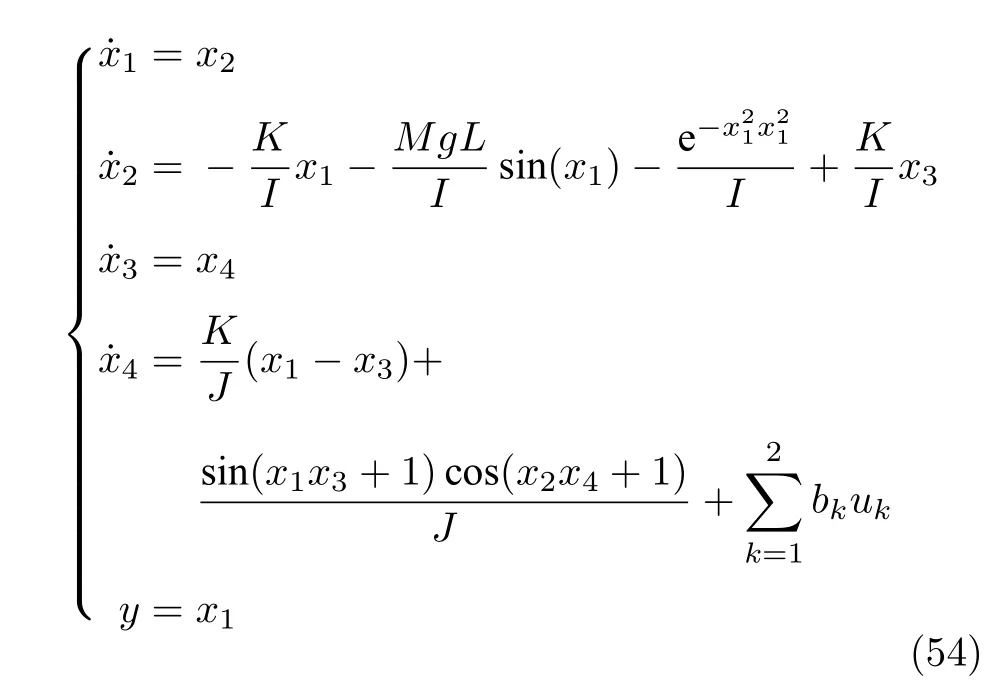
其中,b1=b2=1/J.在仿真中,系统参数选择为M=2.3,L=1,g=9.8,I=ML2,J=0.5,K=15.

执行器故障模型选择为

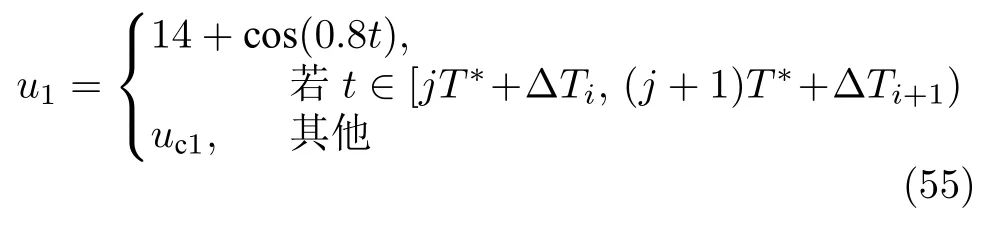
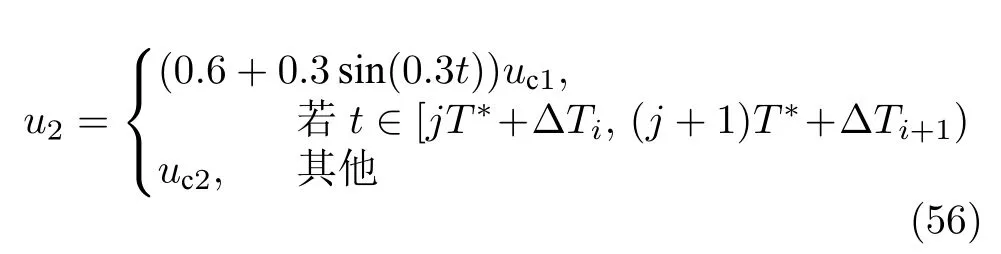
其中,j=1,3,···;T=25.在式 (55)和式 (56)中,加入不等间隔的 0≤∆T1<∆T2<···<∆Ti <∆Ti+1<···,使得均匀间隔周期执行器故障变为非均匀间隔周期执行器故障.从式 (55)和式 (56) 中可看出,在每个 [jT∗+∆Ti,(j+1)T∗+∆Ti+1)s时间段内,系统中第1 个执行器将锁死在u2=14+cos(0.8t),而第2 个执行器的输出将损失其有效性的 30%～90%.在其余时间段内,两个执行器均运行在无故障情况下.

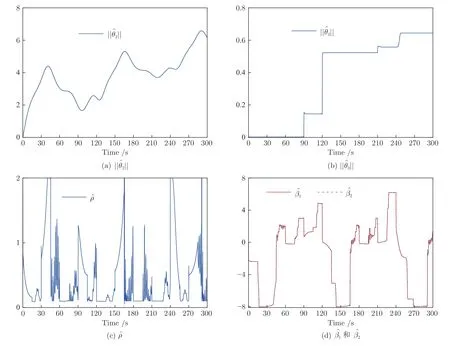
图13 实验3 中自适应参数Fig.13 Adaptive parameters in Experiment 3

首先,图14(a) 显示了系统的输出y可收敛到其期望输出yd的一个很小的领域内.从图14(b)可看出,跟踪误差可渐近地收敛到零的一个很小的领域内.控制增益参数k1,k2,k3,k4和自适应律因子Γ越大,跟踪误差越小,即系统的暂态和稳态指标越好.其次,控制输入信号u1,u2,滤波信号xc2,xc3,xc4,ξ1,ξ2,ξ3和估计参数有界性如图15～17 所示.特别是图17 (a)和图17(b) 显示了估计参数随着参数跳变次数的增加而不断增加.但是,基于投影算子的自适应律能够明确保证的有界性.最后,从图14～17 中可看出,在非均匀间隔周期执行器故障的情况下,所提出的补偿控制器不仅能够驱动系统完成预期的跟踪控制指标,而且保证了所有闭环信号的有界性.

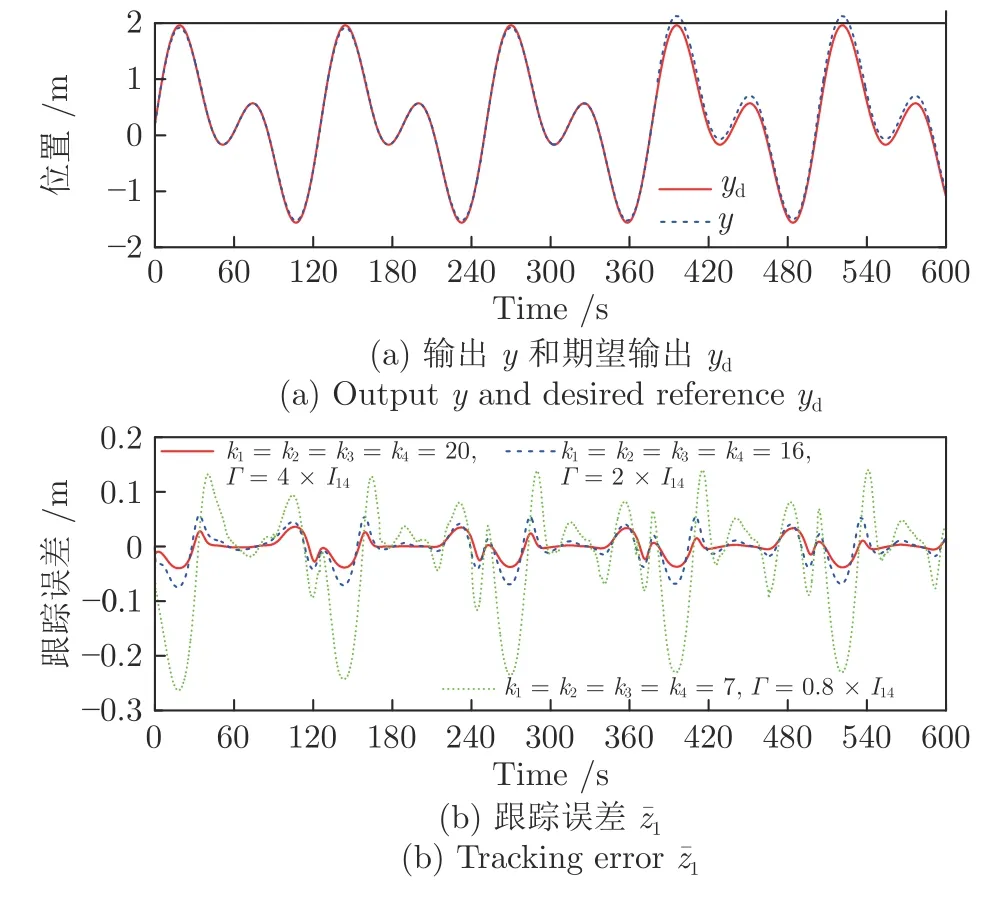
图14 实验4 中输出y ,期望轨迹yd 及跟踪误差Fig.14 Outputy,desired trajectoryyd and tracking error in Experiment 4

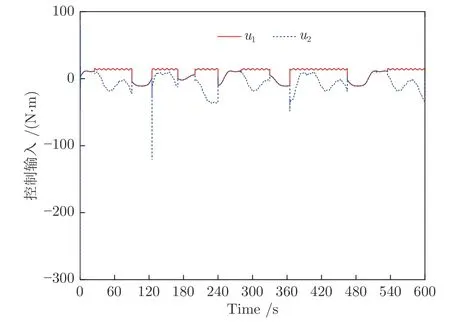
图15 实验4 中控制输入u1和u2Fig.15 Control inputsu1 andu2 in Experiment 4

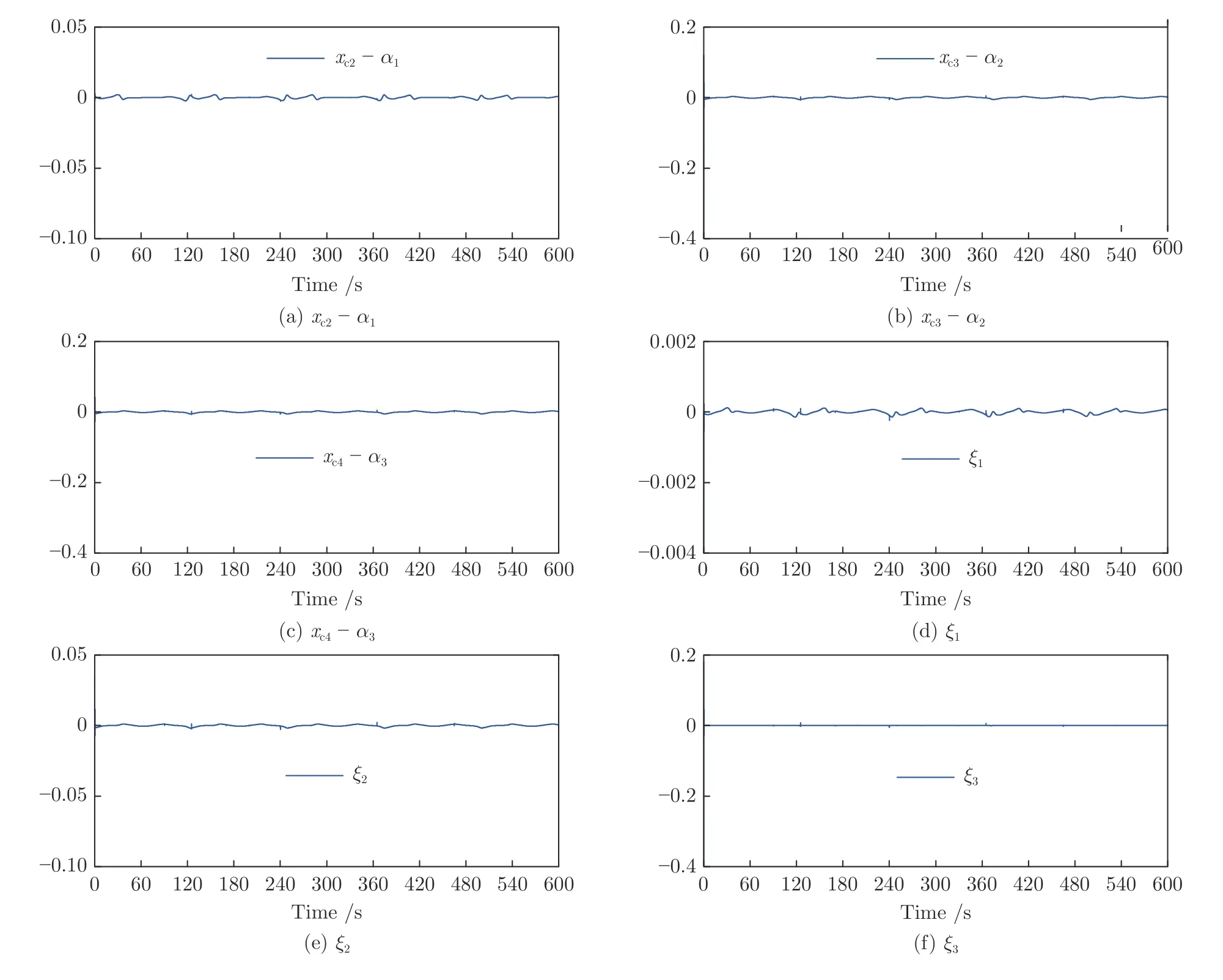
图16 实验4 中命令滤波误差及其补偿信号Fig.16 Command filtered errors and their compensating signals in Experiment 4

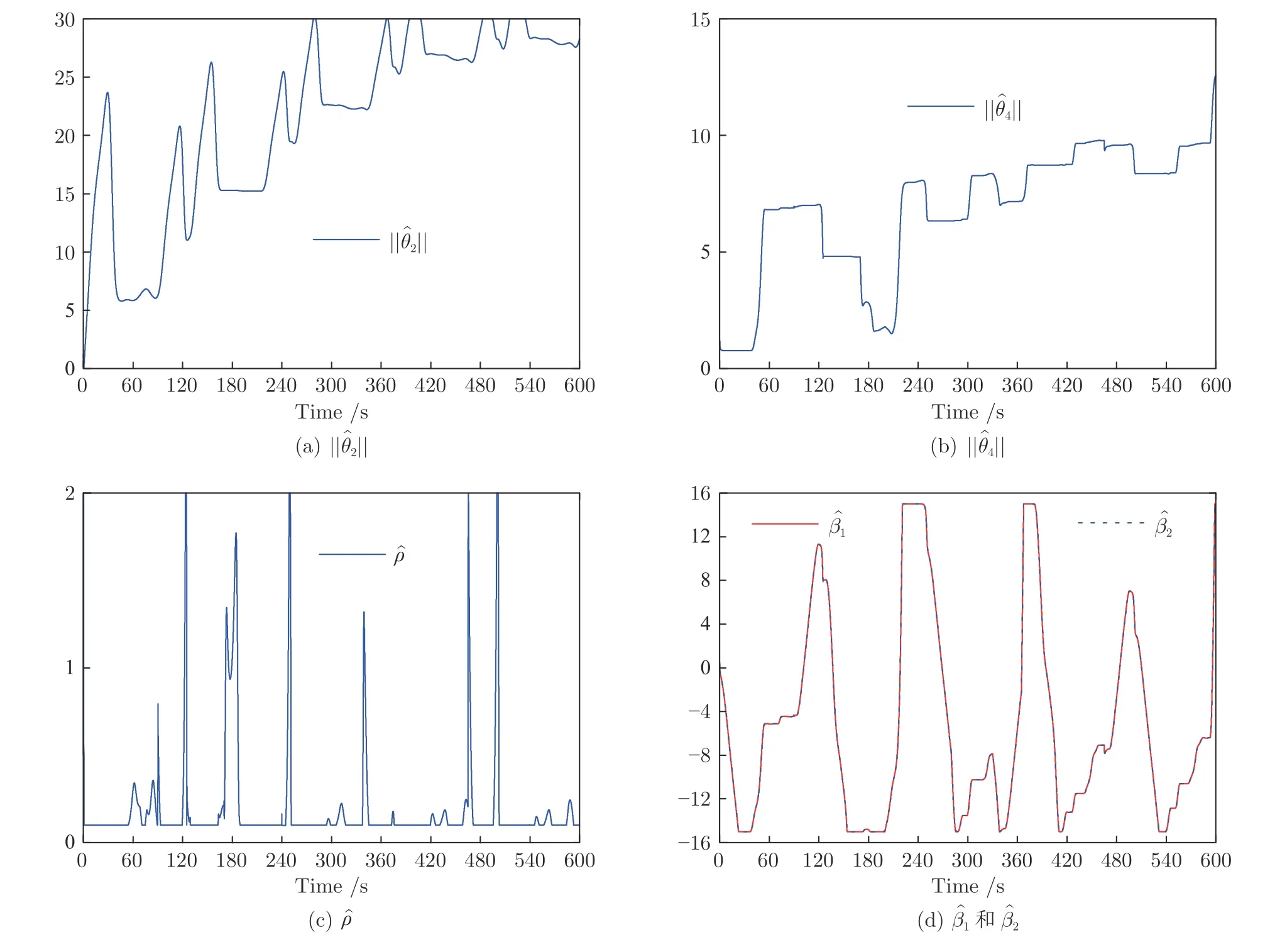
图17 实验4 中自适应参数Fig.17 Adaptive parameters in Experiment 4

4 结束语

本文针对一类不确定严格反馈非线性系统,提出了一种自适应 CFB 控制方案解决了间歇性执行器故障的补偿问题.基于投影算子的参数更新律可保证控制器中估计参数的有界性.即使存在未知参数间歇性跳变的影响,改进的Lyapunov 函数证明了所提出的方案能够保证闭环系统中所有信号的有界性.同时建立了系统稳定性与Lyapunov 函数跳变幅度,最小故障时间间隔以及设计参数之间的关系.进一步,建立的跟踪误差的暂态和稳态指标显式界说明了通过调节设计参数,可获得良好的系统暂态和稳态跟踪指标.最后,四个仿真实例验证了所提出的控制方案不仅解决了均匀间隔周期执行器故障的补偿问题,而且解决了非均匀间隔周期执行器故障的补偿问题.

迟滞或者输入量化等未知非线性现象也经常存在于控制系统的执行器中.因此,结合高增益观测器技术[32],针对具有迟滞(或者输入量化)和间歇性执行器故障的系统(1),设计一种自适应输出反馈控制方案将是下一步的研究重点.

附录A 定理2 的证明

证明.调用式 (31),式 (25) 定义的 Lyapunov 函数V的导数还满足

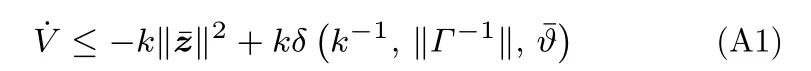
其中,k的定义见式 (27).