一种变分模态分解和频域积分相结合的故障特征提取方法

曹增欢,王国锋,户满堂,盛延亮

(天津大学 机械工程学院,天津 300350)

在旋转机械的振动测量中,加速度传感器由于体积小、灵敏度高、频率范围宽等优点而被广泛使用。而设备的健康监测、振动评估标准常以速度、位移信号为主,例如ISO2372国际振动标准和ISO7919轴振动评价标准就以速度有效值、位移峰值进行评估,因此在实际应用中,常需要对加速度信号进行积分以获取位移、速度信号。

积分方法包括时域积分和频域积分两种。时域积分多是基于离散信号的数值积分,常采用的有梯形公式、辛普森法则等[1]。程启清等[2-3]通过对加速度信号进行时域积分生成位移信号,证实了时域积分过程中的趋势项和直流分量对精度的影响问题,同时信号中存在的噪声信息也会对积分后信号产生干扰,使得积分结果误差较大。许晓红等[4]将牛顿-莱布尼兹公式和辛普森公式相结合,提出了一种组合辛普森积分方法,采用地震波测试数据验证了算法的有效性,提高了计算精度。针对时域积分中产生的累积趋势项问题,陈道云等[5]提出了基于经验模态分解的时域二次积分方法,实验结果表明该方法有效去除了趋势项,然而经验模态分解自身存在的端点效应和模态混叠问题并没有得到有效解决。王万金等[6]提出了一种时域积分与最小二乘方法相结合的方法,消除了零漂对积分结果精度的影响。杨贵春等[7]研究了基频对信号积分的影响,通过对发动机振动信号进行小波阈值去噪并重构,再进行二次积分,验证了积分结果的准确性。

与时域积分相比,频域积分避免了在时域内多次积分时需多次去趋势项的繁琐,同时有效地减小了累计误差的放大[8]。Brandt和Brincker[9]通过研究频域积分方法,提出了一种加权叠加积分法,仿真结果表明该方法对多数情况下的稳态信号更为适用,提高了积分精度。Zhu等[10]提出了一种基于低频衰减的频域积分方法,并提出了3种误差评判指标来控制积分精度,仿真结果验证了该方法的优越性。方新磊等[11]针对信号中含有直流分量和干扰噪声的问题,提出了基于低通滤波和带通滤波的频域积分算法,实例验证了该方法可以较好地去除低频趋势项和高频干扰噪声。胡玉梅等[12]针对二次积分中的趋势项误差问题,采用低频衰减算法对加速度信号进行积分,并利用积分精度控制方程保证积分精度。实验研究表明,该算法可有效控制趋势项误差,然而当加速度信号基频较低时积分误差较大。针对加速度信号中的噪声问题,陈太聪和张奇[13]提出一种基于频谱能量形态拟合与频域积分结合的有效频段法,相对于传统频域积分法,有效频段法可以实现积分频段的自动确定,获得更高的积分精度。成勋等[14]提出了小波分解和时频域积分结合的方法,通过实例和误差指标验证了该方法的积分效果。文献[15-16]中提出了一种基于有效信息重构的故障旋转机械振动加速度信号积分方法,实验结果表明,该方法在去噪和保留有效特征信息方面,比传统积分方法具有更高的优越性。

通过以上分析,频域积分在计算复杂度、累计误差、趋势项和直流分量的抑制等方面要优于时域积分,但仍然存在趋势项误差和噪声干扰的问题,尤其对非平稳信号的低频部分表现明显。另外传感器的测量误差、环境噪声影响等因素,均会影响到积分结果的准确性。因此针对于频域积分中存在的问题,以及变工况下旋转机械振动信号的非平稳特性,研究一种变分模态分解(VMD)和频域积分相结合的故障特征提取方法,提出采用基于最大峭度特征的方法选择最优模态数以保留非平稳故障信号的有效信息,增强噪声的鲁棒性。经仿真与实验数据验证了该方法的准确性及可行性。

1 方法原理

1.1 频域积分原理

频域积分是一种在信号频域上进行积分的方法。首先对加速度信号作傅里叶变换,将时域信号转换为频域信号,进而在频域中进行积分,最后将积分后的频域信号转换为时域信号。

设离散信号的周期长度为N,采样间隔为Δt,频率分辨率为Δf,则傅里叶正变换为

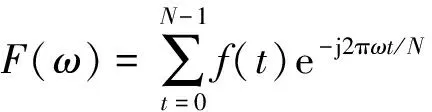
(1)

傅里叶逆变换为

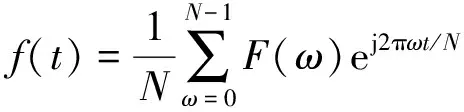
(2)

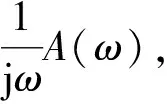
将各个频率的傅里叶分量在频域中进行积分后,再通过傅里叶逆变换转换到时域,得到积分后信号。设实测振动加速度信号为{x(t)}(t=1,2,3,…,n),则其一次积分的计算公式为

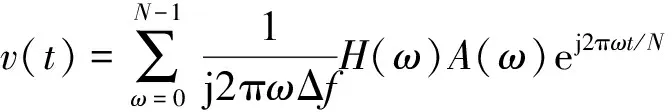
(3)

二次积分的计算公式为

(4)

其中:

式中:fd和fu分别为截止频率下限和截止频率上限;Δf为频率分辨率。

1.2 变分模态分解原理

变分模态分解(VMD)是一种自适应的信号分解方法,其本质是将原始信号分解成若干个不同的本征模态分量(Intrinsic mode component, IMF),每个分量具有不同的中心频率和带宽,通过迭代搜寻变分模型的最优解,来确定每个分量的中心频率和带宽。VMD算法包含两个主要部分,即变分模型的构建和变分问题的求解。

1)变分模型的构建

计算混合后信号的梯度L2范数,并估算出各模态的带宽,构建约束模型如下:

(5)

2)变分问题的求解

为求解上述变分模型,引入二次惩罚因子α和拉格朗日乘法算子λ,求解变分问题的增广Lagrange函数L({uk},{ωk},λ),其表达式为

(6)

通过反复迭代计算,直至找到拉格朗日函数的鞍点,即为最优解。

1.3 峭度因子

峭度因子(Kurtosis factor,KF)是反映随机变量分布特性的数值统计量,是归一化的4阶中心矩。峭度指标是无量纲参数,对冲击信号特别敏感,特别是早期故障的诊断。当设备无故障运转时,峭度指标小于3,当故障严重时,峭度值随之增大。本文采用最大峭度指标来选择分解后的最优模态数。峭度因子表达式为

(7)

式中:x为振动信号;μ为信号的均值;σ为信号的标准差。

1.4 皮尔逊相关系数法

皮尔逊相关系数法是一种度量两事物间相关程度的方法。相关系数越接近于1或-1,表明相关性越强;反之越接近于0,表示相关性越弱。为判别各个IMF分量与原始信号的相关度,采用该方法进行相关系数度量。计算公式为

(8)

2 方法步骤

该方法主要包含4个方面,基于VMD算法的原始加速度信号分解、最大峭度准则选取最优模态数K值、皮尔逊相关系数法确定最优IMF分量、最优IMF分量频域积分。信号分析流程如图1所示。

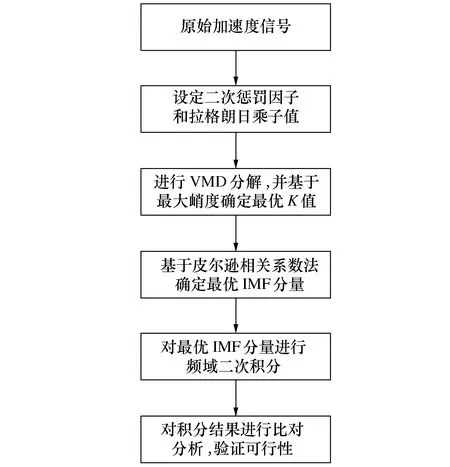
图1 信号分析流程图

信号分析流程步骤如下:

1)通过加速度传感器获取振动加速度信号。设定分解参数:二次惩罚因子α=2 000和拉格朗日乘子λ=0。

2)基于最大峭度准则选取最优模态数K。设定初始模态数为2,步长为1,计算各个模态数K下的各个IMF分量峭度值KFk(k=1,2,3,…,K),取最大峭度值KFmax作为该模态数下的峭度,最大峭度值所对应的模态数即为最优模态数K。

3)通过皮尔逊相关系数法计算各IMF分量与原始信号的相关度ρuk(t),a(t),并选取相关度最大的IMF分量作为最优分量。

4)对最优分量进行频域二次积分,得到位移信号,进行故障特征提取与诊断。

3 仿真分析与验证

3.1 仿真信号构造

仿真一种复杂耦合情况下的旋转机械振动情况,信号转频设定为30 Hz,同时在信号中加入直流分量。加速度信号a(t)与时间t的函数关系式为

a(t)=0.04cos(2π×6t+150π/180)+

0.25cos(2π×30t+36π/180)+

0.18cos(2π×60t+45π/180)+

0.032cos(2π×90t+80π/180)+

0.014cos(2π×120t+120π/180)+0.05

(9)

设定采样频率为1 024 Hz,采样点数为1 024。为了更接近于实际作业环境,在信号中加入信噪比为10 dB的高斯白噪声。

由加速度仿真信号a(t)通过两次积分所得理论位移信号x(t)的表达式为

x(t)=-0.06/(12π)2×cos(2π×6t+150π/180)-

0.25/(60π)2×cos(2π×30t+36π/180)-

0.18/(120π)2×cos(2π×60t+45π/180-

0.032/(180π)2×cos(2π×90t+80π/180)-

0.014/(240π)2×cos(2π×120t+120π/180)

(10)

仿真加速度信号、理论积分位移信号如图2和图3所示。

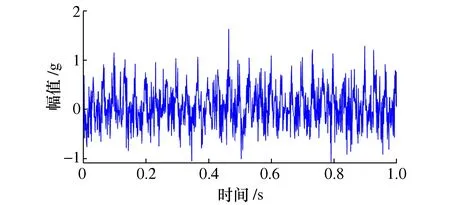
图2 仿真加速度信号时域图

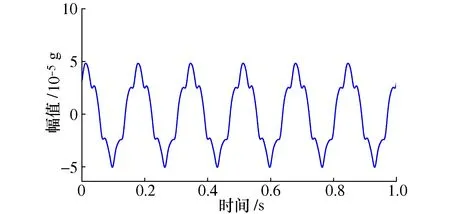
图3 理论积分位移信号时域图

3.2 仿真信号分解

设定二次惩罚因子α=2 000和拉格朗日乘子λ=0,初始模态数K=2,模态数依次递增K=K+1,直至K=10。计算各阶模态数下的各IMF分量峭度值,选取最大峭度KFmax作为该模态数下的最大峭度值,如图4所示。

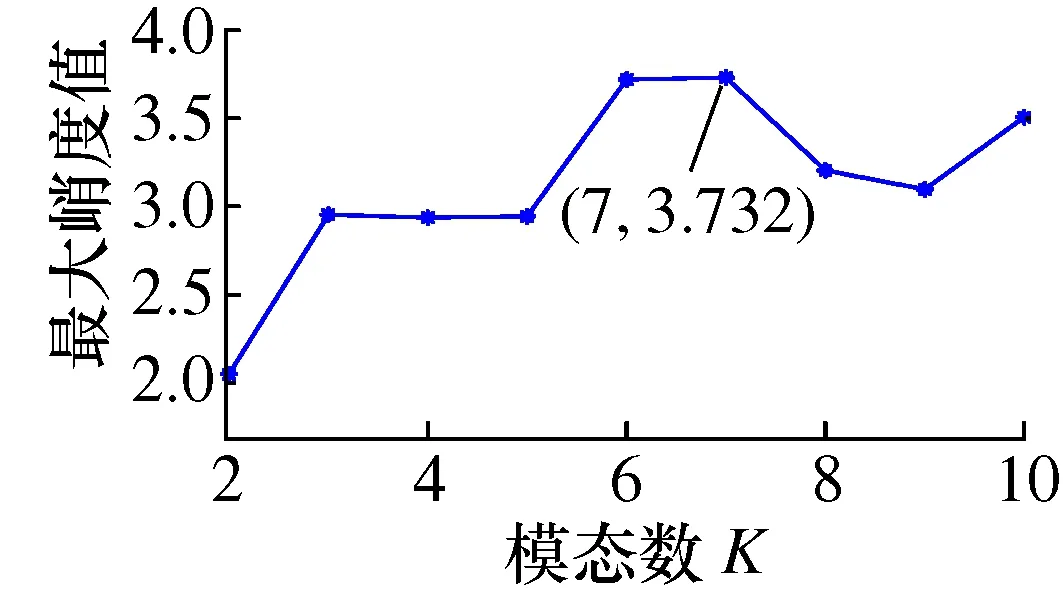
图4 模态数与最大峭度关系图

由图4可知,K=7时峭度值最大,故选取K=7作为最优模态数进行分解,并根据皮尔逊相关系数法则计算各IMF分量与仿真加速度信号的相关系数ρuk(t),a(t),各分量相关系数如表1所示。

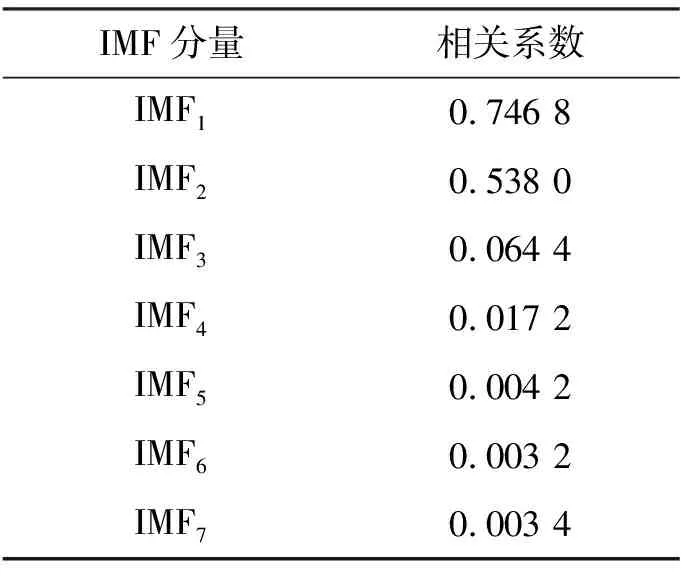
表1 K=7时,各分量相关系数表

由表1可知,IMF1分量的相关系数最大,故选取其作为最优分量。

3.3 最优IMF分量积分与验证

对仿真加速度信号a(t)及IMF1分量分别进行频域二次积分,得到两位移信号时域图如图5所示。

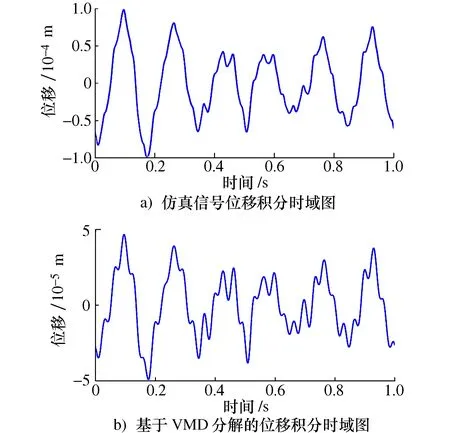
图5 频域二次积分时域图

对比图3与图5可看出,基于VMD分解后的位移积分信号更接近于理论积分信号,而由于信号中存在的噪声干扰以及积分过程中产生的趋势项问题,直接积分得到的位移信号幅值误差更大,降低了有效信息的辨识度。

为了便于定量地分析与评价,采用平均峰值误差、平均最大相对误差以及平方和误差作为评判指标进行评定,结果如表2所示。

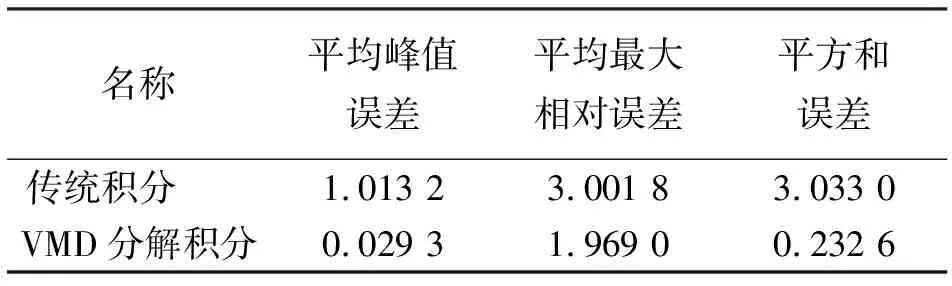
表2 误差评价表

从表2中可以看出,基于VMD分解后的积分信号的3项误差指标均更小,结果表明该方法能够有效地降低噪声及积分过程中趋势项带来的影响,并且累计误差效应得到了明显的改善,比传统方法具有更高的积分精度,证明具有较好的可行性。

4 实验分析与验证

4.1 实验测试

所用实验数据来自于某研究所自行设计加工的滚动轴承试验台。该试验台包括了调速器、驱动电机、动力箱、滚动轴承安装架、轴向加载装置和径向加载装置等部分。该实验采用的轴承为6308深沟球轴承,具体参数如表3所示。轴承状态有5种,包括轴承状态良好、轴承外圈有剥落、轴承内圈剥落、轴承滚珠剥落以及轴承保持架断裂,从中选取外圈故障的信号进行验证。

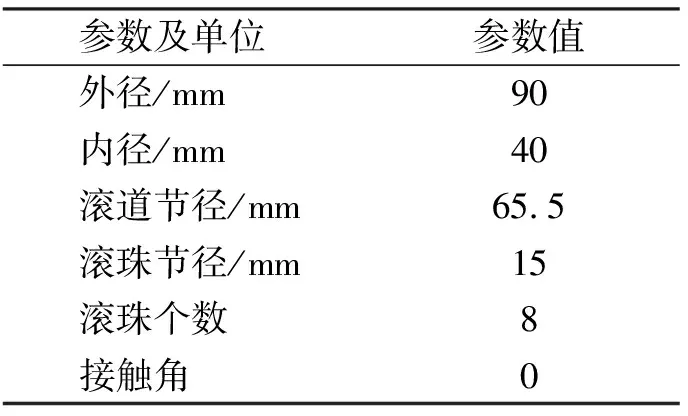
表3 6308轴承参数表

采样频率为10 240 Hz,采样点数为20 480。在电机转速为1 309 r/min下,该轴承外圈故障频率为67.28 Hz,转频为21.82 Hz。实验数据振动加速度时域图如图6所示。

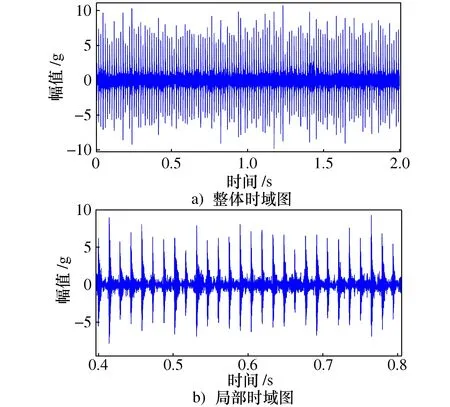
图6 外圈故障加速度信号时域图

4.2 信号分解

在对振动加速度信号进行VMD分解前,设定二次惩罚因子α=2 000和拉格朗日乘子λ=0。模态数初始值K设为2,步长为1,模态数依次为K=K+1,直至16。计算出各模态数下的各分量峭度值,并选取最大峭度作为该模态数下的峭度,如图7所示。

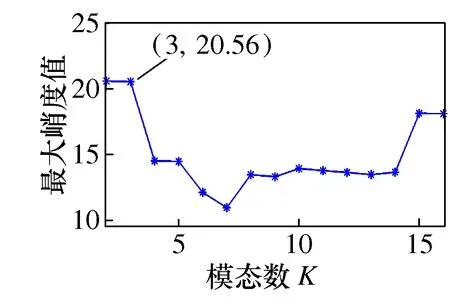
图7 模态数与最大峭度关系图

由图7可知,K=3时,峭度值最大,故选取K=3作为最优模态数,其VMD分解结果如图8所示。

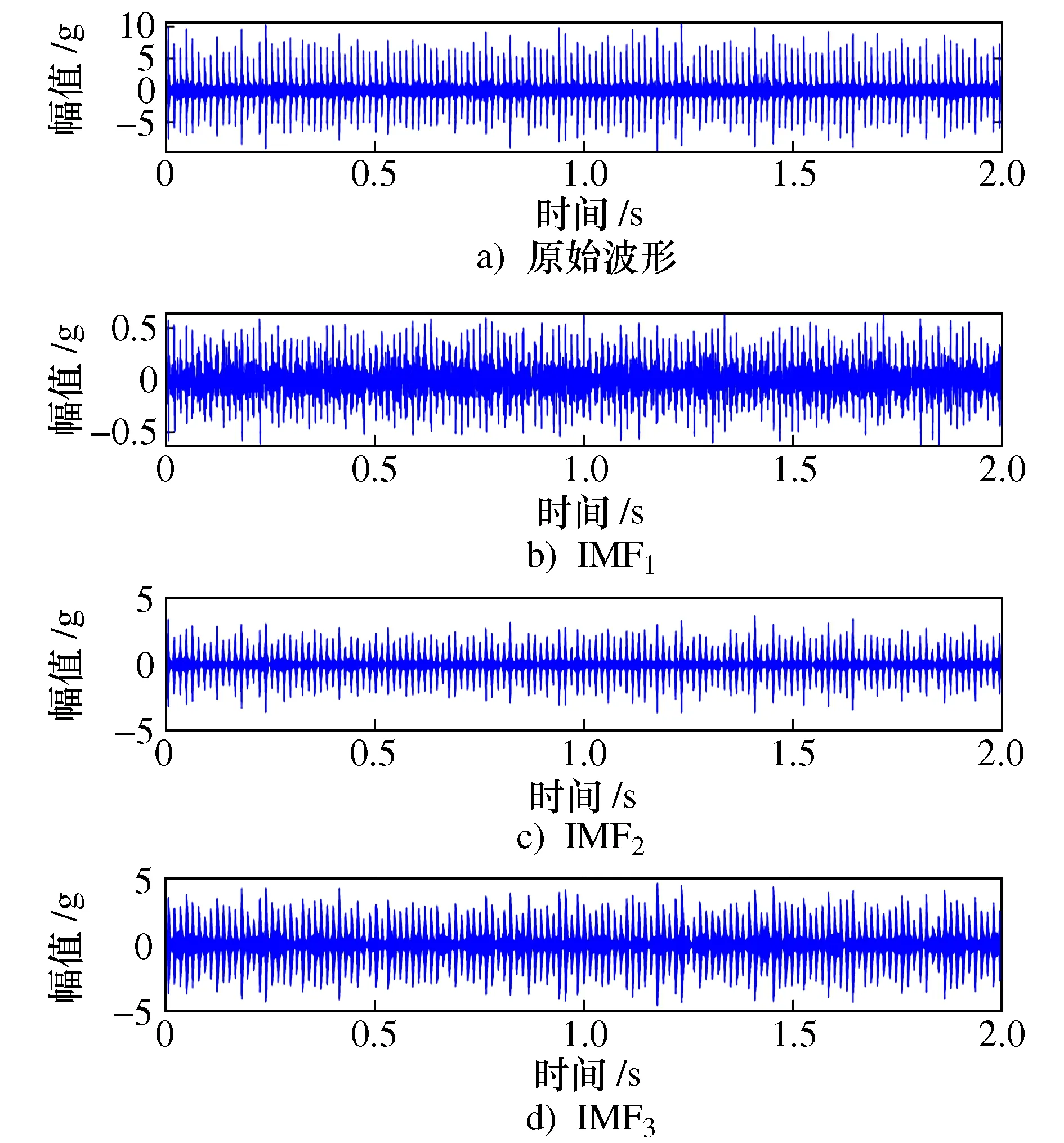
图8 VMD分解图

根据皮尔逊相关系数法,分别计算K=3下的各个IMF分量与原始信号的相关系数,如表4所示。

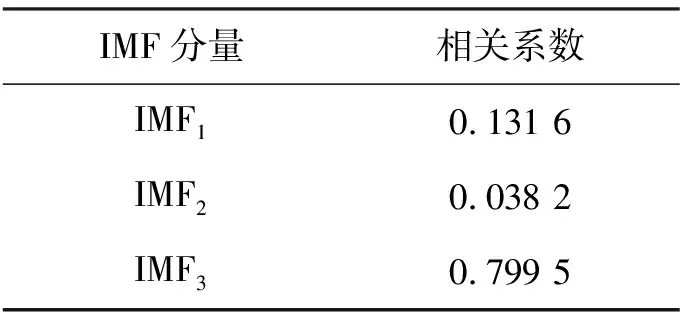
表4 K=3时,各分量相关系数表

由表4可知,第3个IMF分量与原始信号的相关性最高,故选其为敏感IMF分量。

4.3 敏感分量积分与验证

首先对原始信号进行频域二次积分,如图9a)所示,再对K=3的IMF3分量进行频域二次积分,如图9b)所示。

对比图9可以看出,由原始信号直接积分所得的位移信号,其有效信息丢失严重,且基频成分对积分结果影响较大,信号变形严重。而基于VMD分解后所得的位移信号,很好地保留了原始信号的振动信息,减轻甚至消除了基频的影响,清晰真实地呈现出了周期和相位等信息,证明该方法具有良好的可行性。

两积分位移信号的包络图如图10所示。

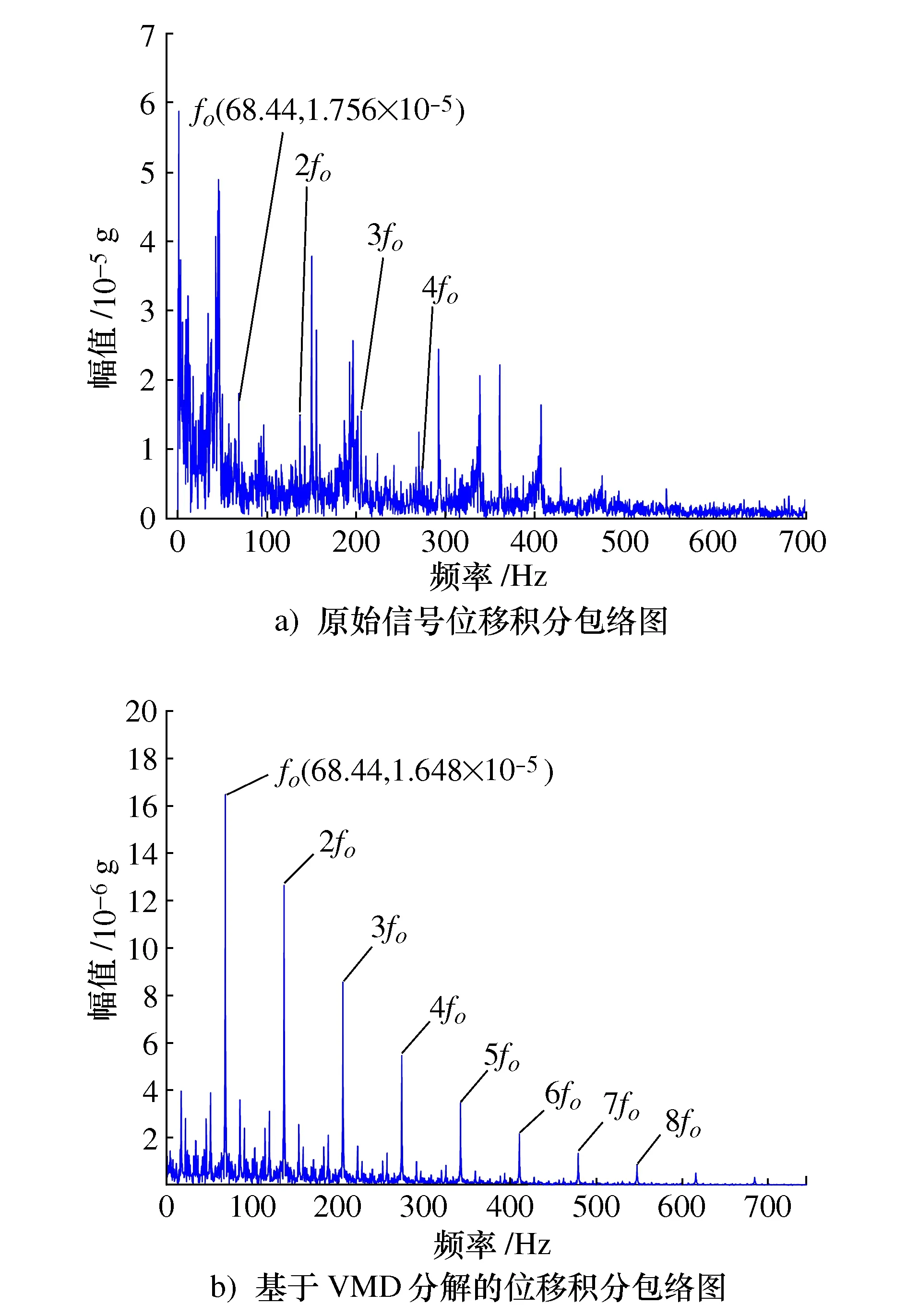
图10 频域二次积分包络图

从图10中分析可知,由原始信号直接积分所得的位移信号,在其外圈故障频率68.44 Hz及其倍频成分有尖峰出现,但受其他杂波频率影响,被淹没在其中难以准确辨识。而基于VMD分解后的位移信号,其外圈故障频率及其倍频成分很好地提取了出来,且直至8倍频处均有明显的尖峰存在,为旋转设备的故障诊断提取了更多的有效信息,从而进一步验证了该方法的可行性。

5 结论

提出了一种变分模态分解和频域积分相结合的特征提取方法。通过仿真和实验分析表明,该方法较好地提取并保存了振动信号中的有效信息,同时抑制了低频信号及噪声信号的干扰,减小了二次积分时产生的趋势项,使得积分信号中故障信息的辨识度更为精准,比传统的频域积分具有更好的实用性。