IVP模型在AUV路径规划与实时避障中的应用研究

李聪,胡超芳,沈同圣,赵德鑫

(1.天津大学 电气自动化与信息工程学院,天津 300072;2.国防科技创新研究院,北京 100071)

近些年,随着自主水下航行器(Autonomous underwater vehicle, AUV)自主平台、传感器、通信以及智能算法的飞速发展,使得AUV在水下爆炸物等危险物品探测领域发挥着越来越重要的作用,而路径规划和实时避障能力是AUV的两项关键技术,也是完成AUV水下作业任务的重要基础[1-2]。AUV路径规划任务通常分为全局路径规划和局部路径规划,当AUV进行水下目标探测作业时,通常需要根据待搜索区域水下环境的先验知识,预先对AUV进行全局路径规划,而后再根据感知到的环境信息、自身的健康状况以及目标信息,采用局部路径修复技术,使AUV可有效跟踪水下目标,保证其高效的水下作业[3-4]。学者们在局部路径修复研究方面做了许多的工作,文献[5]提出利用基于行为的控制体系结构,通过对行为进行矢量求和获得移动机器人的控制决策,有效解决了传统的感知-计划-行动控制回路维护单一世界模型的不足。文献[6]基于行为体系结构,通过对每个可能的控制动作进行投票,选择每个变量的单独决策来确定移动机器人的路径。但是对于移动机器人的耦合控制变量,例如速度和航向变量,对其进行解耦控制容易造成较差的整体行为,存在控制决策选择的困难。为了解决这一问题,通过对自主机器人所有可能的动作进行评估,每个行为都将在公共的决策空间上产生一个目标函数,将自主机器人动作选择问题视为一个多目标优化问题[7-8],但是对自主机器人所有可能的动作进行评估是一个计算量非常大的工作,决策空间也会随着决策变量的增加呈指数增长,难以及时产生控制决策。

针对上述方法的不足,本文设计了在MOOS体系下利用区间优化(Interval programming, IVP)模型进行AUV行为的协调。IVP模型是一种表示和求解多目标优化问题的数学模型,在IVP模型中每个行为都会产生一个分段线性定义的目标函数,是对基本线性函数的一个近似,通过各个块(每个函数一个)的组合空间而不是实际的决策空间来进行搜索的算法,并且在每个块中,分段线性函数隐式的对块中包含的所有动作进行了评估[9-10]。根据AUV路径规划中实时避障的要求,设计路径点跟踪行为、实时避障行为,并将环境约束融入目标函数中,利用IVP模型协调行为,完成了指定区域内设定点的路径规划,分析了IVP模型的有效性。

1 路径规划问题建模

1.1 分布式控制体系结构MOOS-IVP

MOOS-IVP体系结构主要用于对无人驾驶的水面航行器和水下机器人等进行自主控制,由Paul Newman和Mike Benjamin共同维护和开发,包括MOOS(Mission oriented operating suite)和IVP Helm两个部分。如图1所示,采用模块化设计和分布式星型拓扑结构将整体功能分离成单独的不同的模块,MOOSDB负责协调所有模块,并且不同模块代码之间完全解耦[11-12]。

图1 MOOS应用程序及其连接

基于模块的设计思想为自主系统的进一步发展提供了更高的可靠性和更短的开发时间[13]。其中MOOS的核心是MOOSDB数据库,主要用于协调MOOS体系中运行的独立的MOOS应用程序,所有的MOOS应用程序模块彼此之间不能相互通信,必须通过MOOSDB数据库以“发布-订阅”的方式来获取各自所需的数据信息。

1.2 行为控制下的IVP Helm

IVP Helm作为一个独立的MOOS应用程序主要用于协调它自身内部运行的多个自治行为,它的核心是用于管理行为的多目标优化求解器,用于生成行为集的最终控制决策。AUV航迹的控制决策所需要的信息由MOOS-IVP体系中的各个应用程序提供,并将产生的信息以邮件的形式发送到其他应用程序。如图2所示,IVP Helm首先从MOODB获取信息,并放在数据缓冲区中供行为查询使用,为了使行为有效的产生目标函数,需要对行为模式进行声明,通常情况下,AUV任务结构包括一组任务模式M,即

图2 行为求解过程

M={m1,m2,…,mn}

(1)

每个模式都由唯一名称及一组逻辑条件定义,即

mi={n,c1,c2,…,cp}

(2)

行为根据权重信息产生一个目标函数,最后IVP求解器对多个行为目标函数执行多目标优化产生AUV航迹的控制决策。

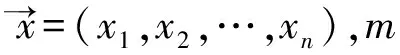
(3)

2 IVP模型中的路径规划行为

2.1 路径点跟踪行为

这里假设AUV工作在同一深度,路径点跟踪行为主要用于在x-y平面上过渡到一组指定的路径点,其中路径点可以以多边形顶点或者割草机路线点的形式在任务启动前直接指定,也可以在AUV运行时动态提供。这里我们以目标为中心设定了一组环绕路径点,并认为以这样方式航行的AUV能够掌握足够多的目标信息,从而间接实现对目标的探测。定义每个路径点周围内径圆和外径圆来确定AUV实际到达某个路径点需要满足的条件,具体思想如图3所示。

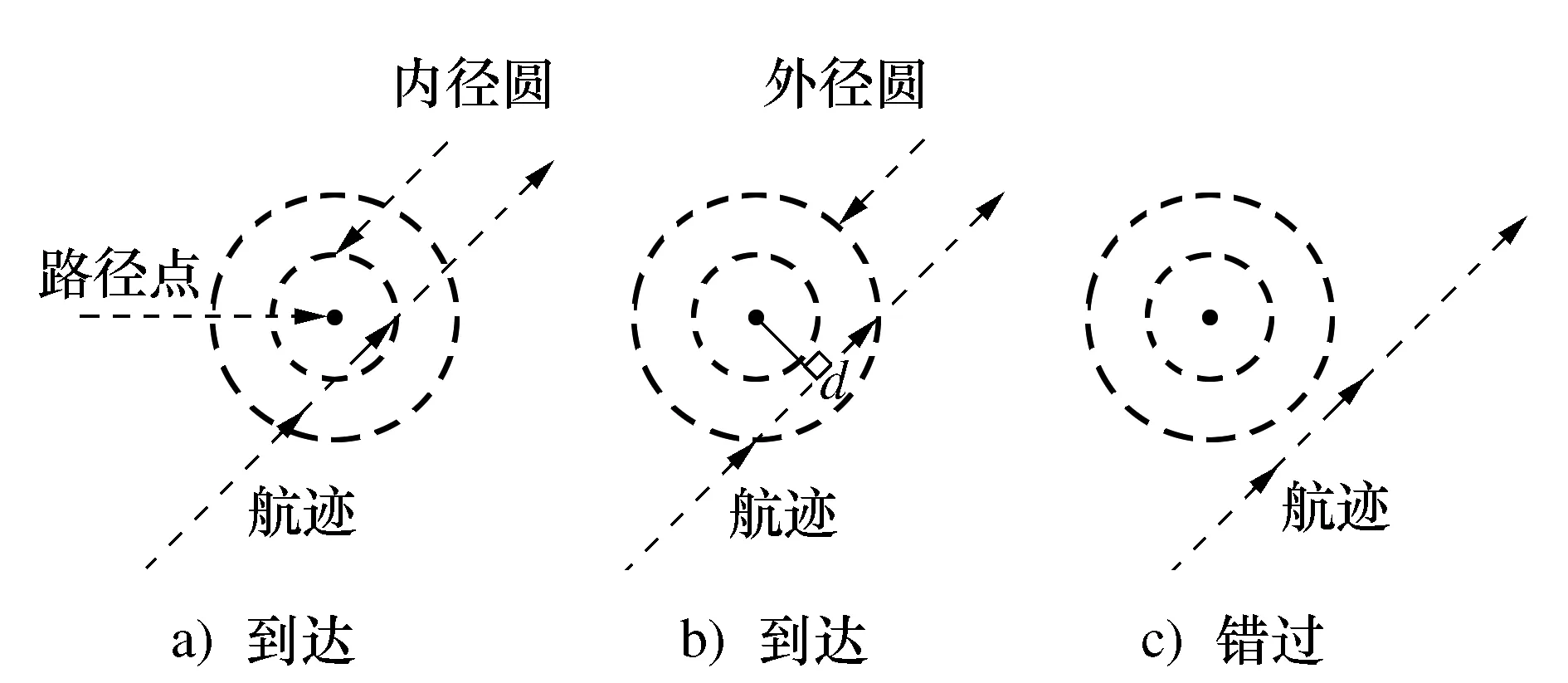
图3 路径点的到达条件

图3a)中AUV通过路径点的内径圆,此时宣布到达路径点;图3b)中AUV错过了内径圆,但是当AUV在外径圆范围内,并且到航路点的距离开始增加时,同样宣布到达;图3c)中AUV既不通过内径圆,也错过了外径圆的范围,此时AUV无法到达当前路径点,也就无法获取路径点的信息。

在两个路径点之间,既可以使AUV简单的转向下一个航路点,也可以根据任务情况驱动AUV转向航迹上的任意一点,具体转向点由跟踪控制引线参数L决定,思想如图4所示。它是从垂直交点d到下一个路径点的距离,定义了轨道线上一个假想的路径点,该行为根据这个假想的转向点输出一个航向,如果引线参数L大于沿着轨线到下一个航路点的距离,则假想的点就是下一个航路点。同时,通过控制AUV与跟踪控制引线的距离h。可以使AUV在有效距离内被拉伸到下一个航路点,以减少轨迹线的超调。

图4 路径点之间的过渡

路径点跟踪行为在IVP Helm的每个迭代中产生一个定义在变量速度和航向上的目标函数,如图5所示,它驱动AUV以接近2 m/s的速度航行到位于90°方向的路径点,圆圈表示航向变量,半径表示速度变量,距离中心越远的位置表示更大的速度值,并且蓝色部分表示不可取值,深红色部分表示行为偏好的控制决策。

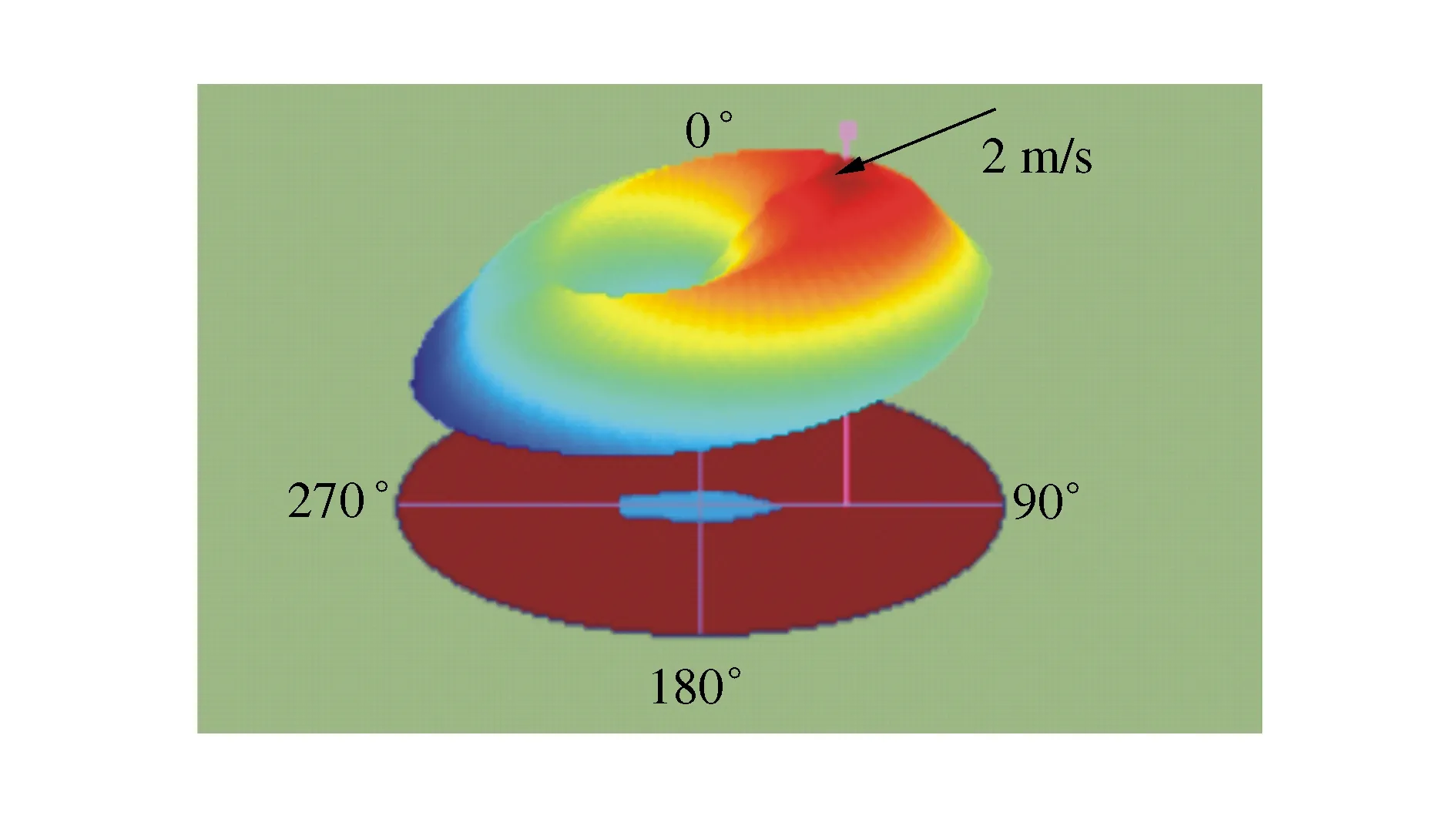
图5 路径点跟踪行为目标函数

2.2 实时避障行为

在AUV路径规划过程中,并非所有的障碍物及其位置在任务加载时就预先知道,只有当AUV及其传感器逐渐接近时才被发现,通过对原路径进行局部路径修复,可以实时有效的处理障碍。文中通过传感器模块标记的动态点簇来表示输入的障碍物,障碍管理器维护一个凸多边形表示来自传感器模块的每一个点簇,并只保留传入的最新的N个动态特征点,即随着新感知点的出现,旧感知点将从障碍管理器的内存中消失。通常情况下,当障碍物的几何形状未知时,采用不规则的凸多边形维护每一个点簇,并且随着障碍物的漂移,多边形也会随之继续增大,从而增加了计算的复杂性。为了简化处理,采用指定径向距离和顶点数的规则多边形维护单个动态障碍点簇,其中多边形以给定点簇中点的平均值为中心,如图6所示。

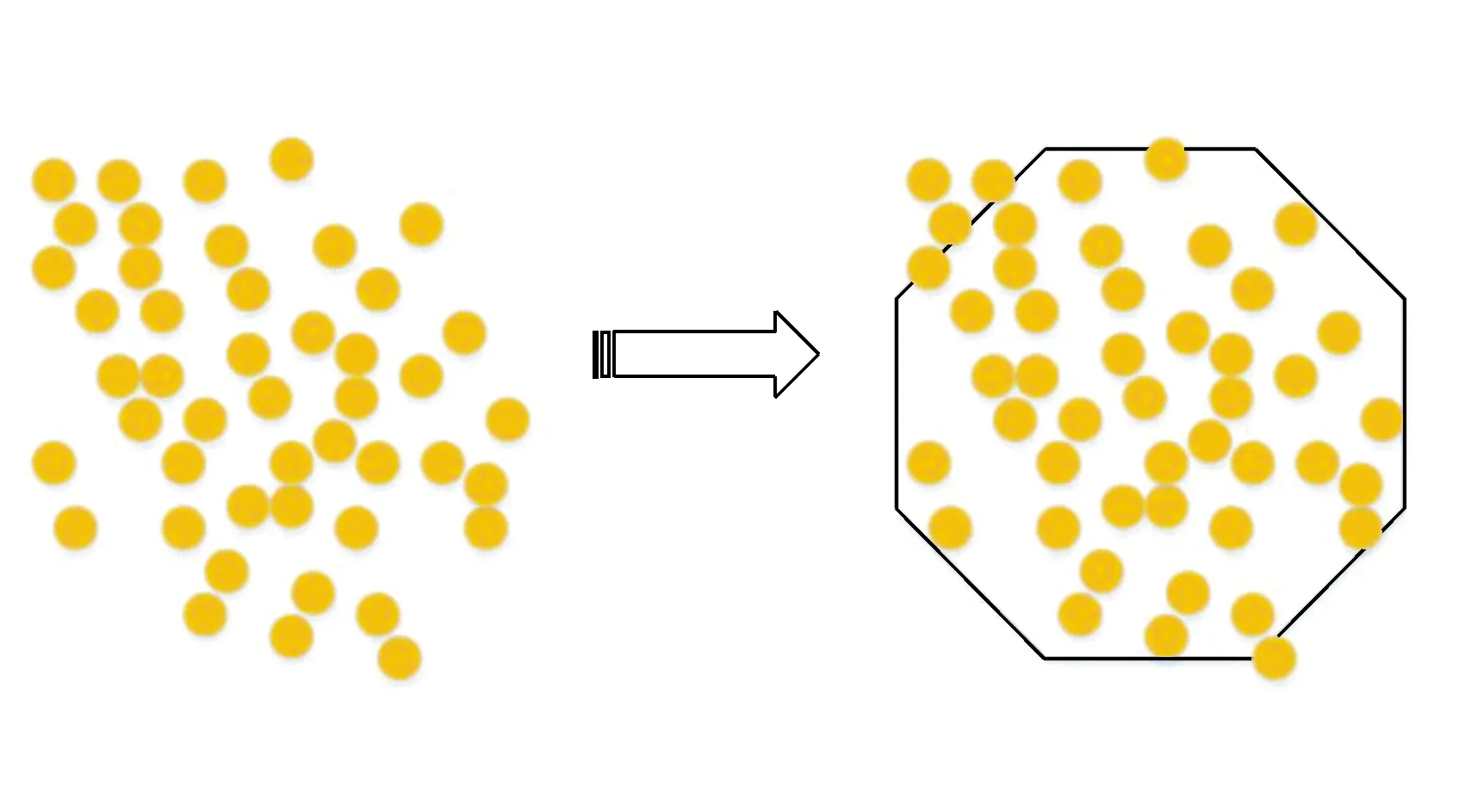
图6 规则多边形近似的障碍物

AUV沿着一组路径点表示的路径航行,当障碍物进入传感器范围时,障碍管理器提供有关障碍物的信息,并促进IVP Helm生成避障行为从而形成经过该区域的局部路径修复。避障行为作为模板存在于IVP Helm 中,在收到关于障碍物的信息之前不会产生任何避障行为,它被配置为在其到障碍物的距离减小时增加优先级,定义了如图7所示的两个距离参数D1和D2,D2直接影响避障行为是否应处于活跃的模式,当AUV和障碍物的距离大于D2时,优先级权重为零,该行为是不活跃的,当AUV在D1范围内时,配置的优先级权重为100%,行为是完全活跃的,而在D1和D2距离之间,优先级权重呈线性方式下降。

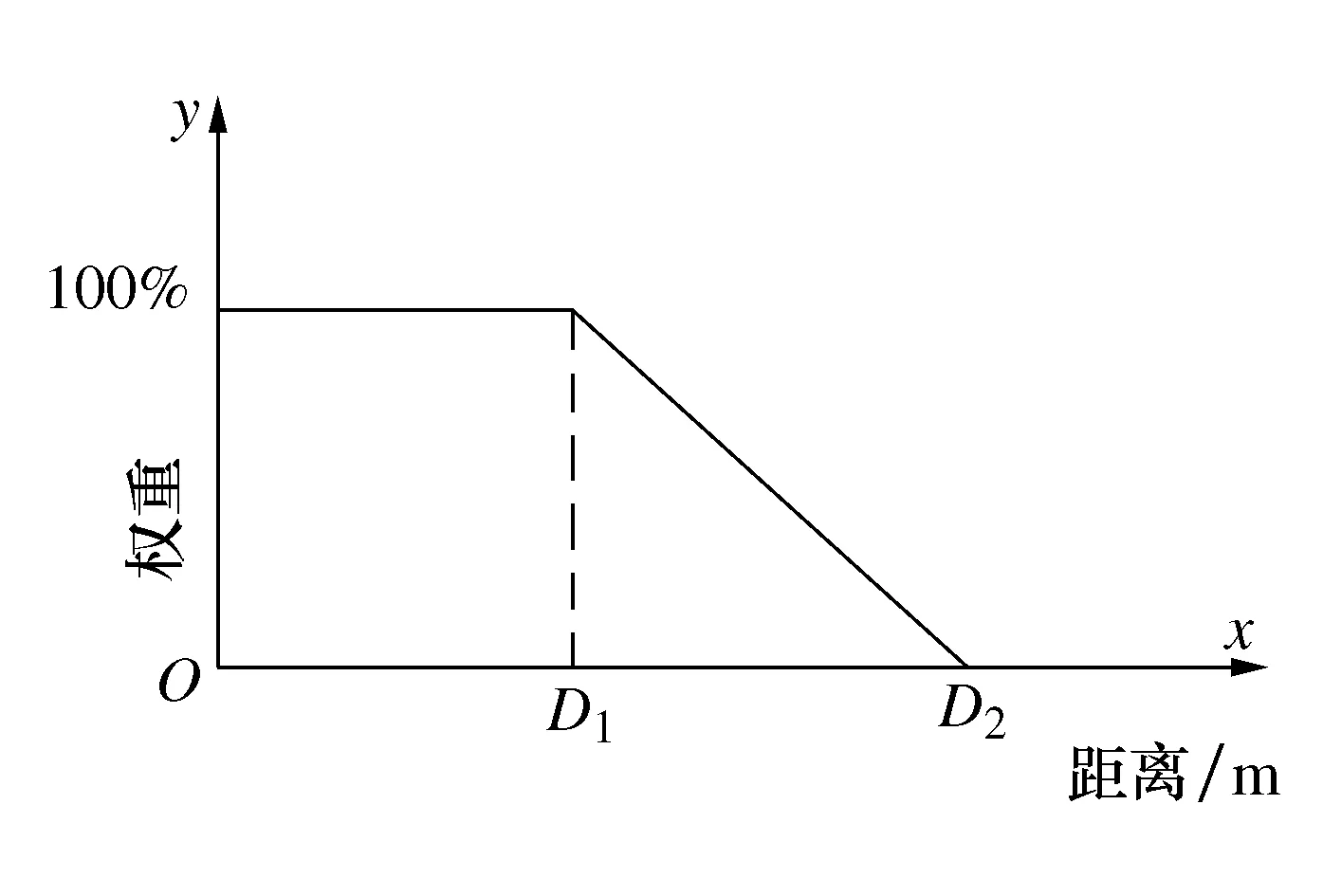
图7 避障行为优先级权重变化过程

考虑到传感器在感知障碍物的大小及其位置时的不确定性以及在利用规则多边形近似实际障碍物的误差,定义了图8中用虚线框表示的缓冲多边形, AUV在避障过程中从缓冲多边形的一边绕到另一边实现避碰,有效的实现了AUV机动安全性和可行路径之间的平衡。

图8 避障实现过程,灰色多边形表示障碍物

避障行为的目标函数定义在速度v和航向θ的笛卡尔积组成的控制决策空间上,其中:

(4)

函数g(x,y,θ,P)为真表示AUV从当前位置(x,y)沿着θ方向航行时与缓冲多边形P不相交。避障行为目标函数形式如下:

(5)

式中:函数h(x,y,v,θ,P)表示AUV从当前位置(x,y)沿着θ方向以速度v航行时与缓冲多边形相交所用时间;tf表示当避障行为活跃时,从当前位置直接过渡到障碍物所能容忍的最大秒数。避障行为产生的目标函数如图9所示,它输出航向大约160°、速度大约为2 m/s的AUV航行控制决策,其中深红色区域表示AUV控制决策的偏好值。

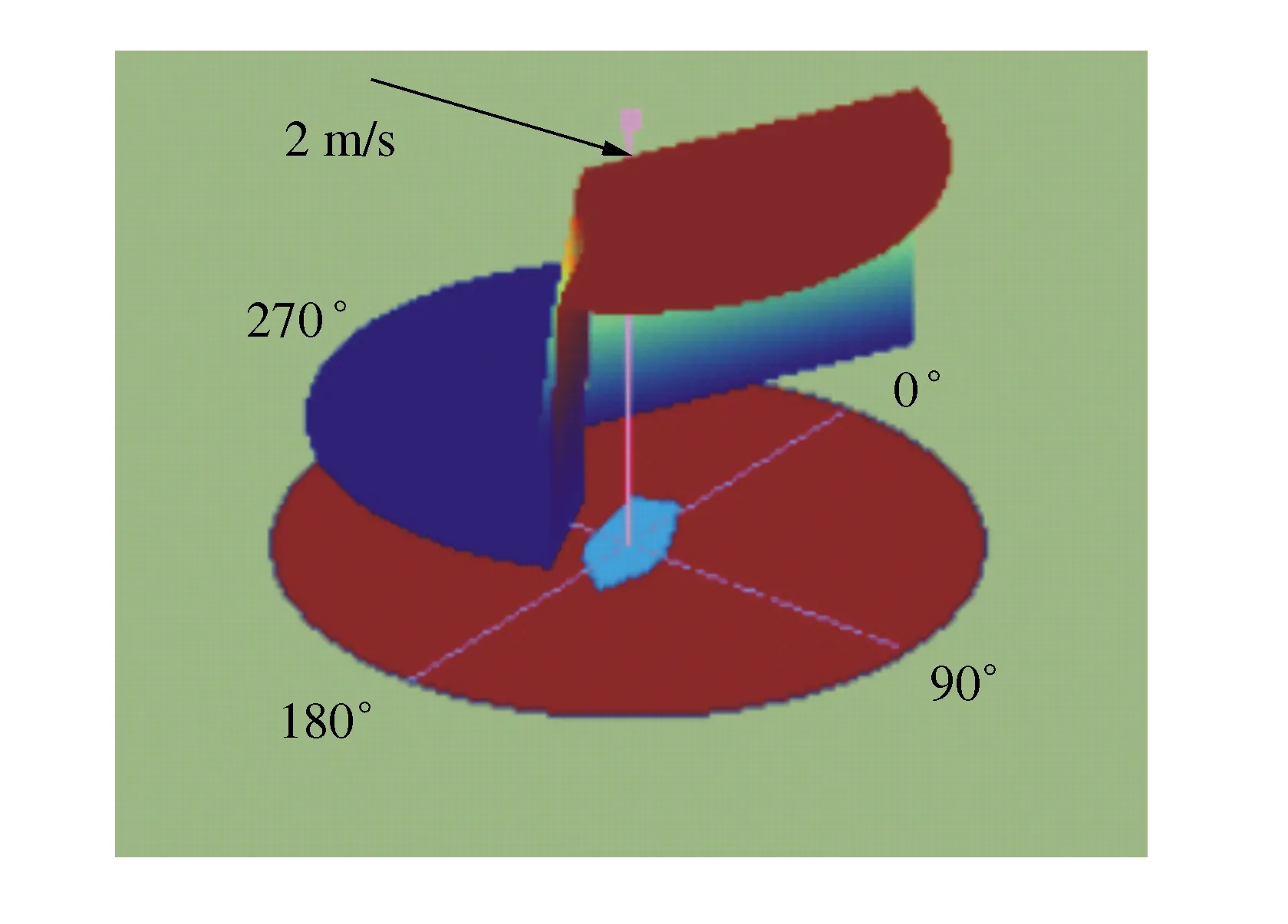
图9 实时避障行为目标函数

3 仿真分析

为了说明上述IVP模型及其控制算法的有效性,采用实际的AUV动力学模型,通过PID控制器进行航行控制,并在MOOS-IVP仿真环境下进行实验验证。图10给出了仿真结果,AUV从初始点(0,0)以期望速度v=2 m/s,初始航向θ=180°出发,最大加速度a1=0.1 m/s2,最大减速度a2=0.1 m/s2,需要跟踪的路径点是分别以目标A=(90,-105)和目标B=(200,-58)为中心,径向距离为30 m的正八边形顶点。为每个路径点定义的参数如下:L=30 m;h=2 m;内径圆半径r1=5 m;外径圆半径r2=10 m。

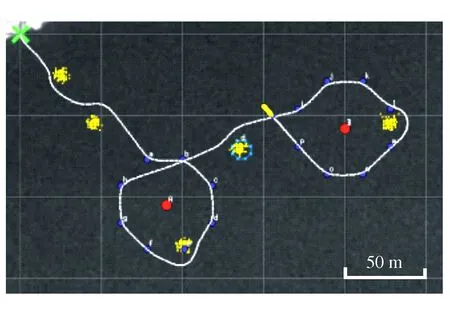
图10 实验仿真结果图

实验中利用径向距离为6 m,顶点数为8的正多边形维护了5个障碍物,配置警报距离参数h1=35 m,当AUV与障碍物的距离进入这个范围时,生成避障行为,定义的其他障碍物参数如下:D1=12 m;D2=20 m;D3=11 m;tf=5 s;N=50个。其中N表示感知并保留最近的障碍物的特征点数,而D3表示图8中缓冲多边形的径向距离。

为了更好地了解避障过程,图11中分别列出了t1、t2、t3时刻对应的目标函数,图中深红色表示AUV偏好的控制决策,而蓝色表示不可取值。

图11 不同时刻目标函数产生的控制决策

图10表明,AUV根据到障碍物的距离范围实时生成避障行为,成功避开障碍物实现对目标A和目标B周围的多边形路径点的跟踪,证明了文中设计的IVP模型和控制算法在AUV路径点跟踪以及实时避障方面的有效性和可行性,图12是对应的速度、航向时间序列图。

图12 速度航向时间序列图

4 结束语

本文研究了AUV的路径规划和实时避障控制问题,介绍了一种新的基于行为的控制方法,将路径规划任务划分为多个具体的行为,设计路径点跟踪行为对以指定位置目标为中心的规则多边形的顶点进行顺时针方式的路径点跟踪,设计实时避障行为避开障碍,并搭建MOOS-IVP体系结构模型,利用IVP模型的多目标优化求解算法进行控制决策选择。最后在仿真分析中,AUV绕开障碍物实现对规则多边形的路径点跟踪说明了本文设计的基于IVP模型的体系结构及其控制算法的可行性和有效性,降低了计算的复杂程度,并保证及时获得最优的结果。