管道攀爬机器人夹持机构设计与优化

邵浩东,肖晓晖

(武汉大学 动力与机械学院,武汉 430079)

电厂中多屏管道应用广泛[1],对电厂多屏管道进行定期检测与维护对生产安全至关重要。目前电厂多屏管道环境主流的检测方式是人工检测,它存在工作强度大、检修效率低、检测盲区等问题[2],采用机器人取代人工进行管道检修已经成为一个迫切的需求。电厂多屏管道环境存在管道密集、环境复杂、空间狭小等特点,机器人在多屏管道环境中运动需具备管间跨越能力。因此,具有空间不连续作业能力的夹持式多自由度管道攀爬机器人(以下简称为管道攀爬机器人)受到关注。

对于管道攀爬机器人,夹持机构的性能直接影响着机器人的攀爬能力和负载能力。机器人夹持机构专用性强,对于不同的夹持对象,夹持机构存在较大差异[3-6]。常见的管道攀爬机器人夹持机构按照与管道接触方式的不同大体可分为:四点接触式、两点接触式和双弧面接触式。寇重光等[7]研制的面向电厂管道的攀爬机器人和江励[8]研制的仿生攀爬机器人的夹持机构均采用四点夹持方式,四点夹持具有方式较强的负载能力,但不具备管道定心功能,在夹持和负载过程中若夹持机构相对于管道存在少量位置偏差,无法自行修正,可能会导致夹持失败;Kim等[9]研究的PiRO和Du[10]研制的攀爬机器人采用两点接触式,两点接触式结构简单,但负载能力弱、稳定性较差;朱海飞等[11]研究的MiniBibot和Faizal等[12]研究的管状爬树机器人的夹持方式均采用双弧面接触式。双弧面接触式夹持机构对特定曲率的夹持对象具有很好的夹持效果,但在接触弧面与夹持对象曲率相差较大的情况下,两者接触面积会大大减小,从而导致夹持效果不理想。

针对以上情况,本文基于三点定心法设计了一种新型管道攀爬机器人夹持机构,该夹持机构与管道间采用三线接触方式,具有良好的自定心能力,可满足多自由度攀爬机器人的夹持需求。本文首先对夹持机构进行机构设计与力封闭性分析,其次进行了连杆机构优化,接着进行了仿真分析,得出夹持机构理论最大负载能力,最后进行机器人负载试验。

1 机构设计与分析

1.1 机构设计

三爪卡盘常用于车床工件夹持,与工件三点接触,具有良好的定心功能。仿照三爪卡盘夹持原理,本文夹持机构与管道采用三线接触夹持方式,夹持机构采用轴对称设计,对称轴单侧采用异构四杆机构,如图1所示。

图1 夹持机构示意图

图1中:1～7为7个构件,其中构件7为机架,构件1为原动件,其余构件为从动件。该机构有6个转动副、2个移动副和1个螺旋副,机构中所有构件只做平面运动,因此根据平面机构自由度计算公式F=3n-(2Pl+Ph)可得该机构的自由度为1。

1.2 力封闭性分析

机器人对夹持机构的作用力随着机器人运动状态的改变而改变,为了达到负载平衡,夹持机构必须具有封闭的力学模型。夹持机构在夹持管道时与管道之间是线接触,线接触模型可由力螺旋基与摩擦锥来表示,因此可用力螺旋理论分析夹持力封闭性[13]。为了方便分析,取接触线中点为作用点,建立接触点坐标系Ci,建立物体坐标系Co,如图2所示。

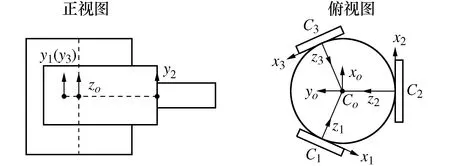
图2 物体坐标系与接触点坐标系示意图

将接触点坐标系下的接触力转化在物体坐标系上,可表示为

(1)

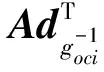
1)至少存在7个6×1矢量(v1,v2,v3,…,v7),且其中6个线性不相关。

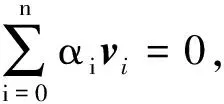
夹持机构与管道之间是线接触,将线接触的作用点定为接触线的中点,每个线接触接触点存在沿x轴和y的摩擦力、沿z轴的接触力和沿x轴和z轴的力矩。因此线接触的接触力由5个矢量组成,分别为:

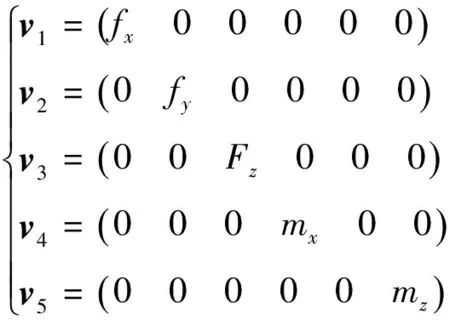
(2)

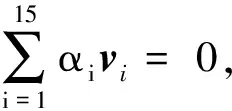
2 连杆机构优化

夹持机构的各个连杆的长度以及结构角将直接决定夹持机构的性能。另外轻量化的设计可增加夹持机构的负载能力,因此夹持机构在满足设计需求的情况下应尽量减轻重量。本文采用遗传算法[15]对连杆机构进行优化,在提高夹持机构性能的同时减轻重量。

2.1 确定优化变量

该夹持机构的夹持目标是直径为65～70 mm管道,夹持机构简图如图3所示。

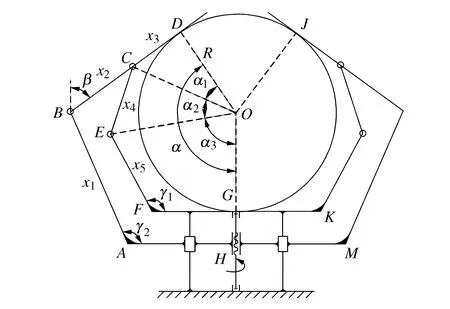
图3 夹持机构简图

图3中:AB连杆设定其长度为x1;BC段长度为x2；CD段长度为x3;CE连杆设定其长度为x4;EF连杆设定其长度为x5;设定EF连杆与FK段所成夹角为γ1,AB连杆与AM段夹角为γ2;FK段和AM段分别为支撑底座和滑台,支撑底座内部有丝杠轴顶部滚珠轴承和直线轴承安装孔,滑台内部有丝杠螺母和直线轴承导轨,两者受限于内部零件结构尺寸,设计中取两者的最小尺寸分别为65 mm和79 mm。以x1,x2,x3,x4,x5,γ1,γ2为设计变量,并限定它们的取值范围:

blow=[15 12 10 12 10 100 100]

(3)

bup=[50 30 30 25 25 120 120]

(4)

式(3)和式(4)分别为变量x1,x2,x3,x4,x5,γ1,γ2取值对应的下限和上限,其中变量x1,x2,x3,x4,x5单位为mm,γ1,x7单位为°。

2.2 确定约束条件

2.2.1 干涉约束

主动连杆和支撑连杆在运动过程中不能发生干涉,根据两者的空间结构,在两者运动过程中不发生干涉需满足如下不等式条件

(x+Ly-x1sinγ2+x5sinγ1)2+

(Lx-x1cosγ2+x5cosγ1)2≥r2

(5)

式中:x为滑台的运动范围，mm;r为连杆铰链直径,mm;Ly为滑台与支撑底座厚度和的一半,Ly=9 mm;Lx为滑台与支撑底座长度差的一半,Lx=7 mm。

滑台与支撑底座厚度均为9 mm,两者在运动过程中不发生干涉需满足滑台与支撑底座间距LGH≥9 mm,即

(x2+x3)cosβ+x1sinγ2-

R(1-cosα1-cosα2-cosα3)≥9

(6)

2.2.2 稳定性约束

为保证夹持机构的定心功能和夹持稳定性,图3中角α取值范围需要加以限定,取α的范围为117.5°≤α≤122.5°,非线性约束方程组为:

(7)

式中:LCO、LEO、LEG、LOG、LFG分别为图4中对应线段长度;R为管道半径,R=32.5 mm;LFG为支撑底座长度的一半,LFG=32.5 mm。

2.3 多目标优化

2.3.1 优化目标

取连杆长度之和为一优化目标,称之为连杆总长F1(x);取丝杆推力F与夹持机构夹紧时与管道接触力FN之比为另一优化目标,如图4所示,称之为有效推力比F2(x)。

图4 夹持机构夹紧状态下受力简图

多目标优化函数方程组为:

(8)

为了减轻夹持机构重量,减少在同等夹持力下丝杆推力,优化过程应以f1(x)和f2(x)取最小值为目标。

2.3.2 优化结果

利用MATLAB遗传算法多目标优化工具箱对夹持机构进行多目标优化,得到Pareto解集合如图5所示。

图5 Pareto解集图

在Pareto解集图中,连杆总长f1(x)减小时导致有效推力比f2(x)增大,反之有效推力比f2(x)减小时导致连杆总长f1(x)增大,权衡两者对夹持机构设计影响,取f1(x)=79.04,f2(x)=2.419为最优解。将连杆长度取整数,并验算式(5)～式(7),得到最终优化解集f1(x)=79,f2(x)=2.53。按照经验法设计的连杆长度与优化后的连杆长度对比如表1所示。

表1 优化前后连杆长度对比

在SolidWorks中建立优化前后的夹持机构模型如图7所示。优化前夹持机构重量为488 g,有效推力比为1.95;优化后夹持机构重量为431 g,有效推力比为2.53。优化后有效推理比相对于优化前增加了29.7%,但重量减轻了11.7%,相对于有效推理比,重量减轻对夹持机构性能提高更有意义,因此该优化结果是可取的。优化后的夹持机构与管道接触点相对于优化前在周向分布更加均匀,提高了夹持机构的侧向稳定性。

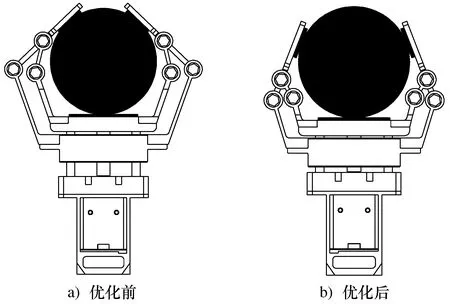
图6 优化前后模型对比

2.3.3 强度校核

为验证优化后的夹持机构的结构强度和可靠性,在ANSYS中对夹持机构做静力学校核,将SolidWorks夹持机构模型导入ANSYS Workbench中,并材料属性、接触与约束、划分网格、添加额定加持力负载。最后得到夹持机构应力应变分布图,如图7所示。

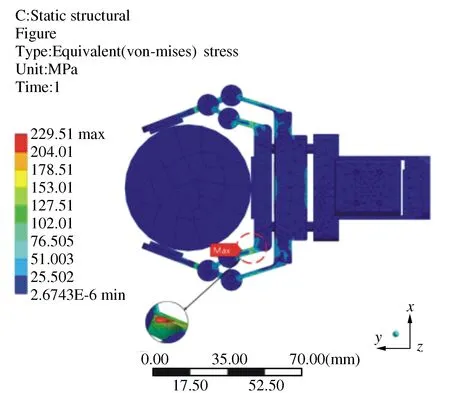
图7 夹持机构应力分布图

夹持机构本体采用7075铝合金,考虑到动载荷,取安全系数为1.8,许用应力为266.67 MPa。仿真结果显示,夹持机构在额定夹持力负载下,最大应力分布在支撑连杆底部倒角处,为229.51 MPa。小于夹持机构最大许用应力。经以上分析仿真,优化后的夹持机构结构强度满足要求。

3 仿真与试验

多关节攀爬机器人在运动过程中施加给夹持机构的负载种类有重力、扭矩和动载荷,机器人在不同的姿态下,施加给夹持机构的负载也不同。夹持机构在受到负载时,夹持连杆在负载作用下会引起连杆形变,较大的变形会导致夹持机构滑落,夹持失败。为了增大夹持机构与管道间的摩擦力,在夹持机构与管道接触面采用橡胶材质,以五自由度攀爬机器人为例探究夹持机构负载性能。

3.1 仿真分析

机器人在管道上的攀爬形式可分为平面攀爬和空间攀爬,平面攀爬即机器人各个关节始终与管道在一个平面内;空间攀爬即管道与机器人关节在三维空间中分布。机器人平面攀爬最大负载发生在机器人各个关节张开,呈直线分布状态下,如图8所示。此时主要负载形式为重力和沿x轴方向的力矩,两者可等效为夹持机构末端的沿z轴负方向的力负载。机器人空间攀爬最大负载发生在机器人各个关节完全张开,呈L型分布在xoy平面上,如图9所示。此时主要负载形式为沿x轴方向的力矩负载。

图8 机器人平面攀爬最大负载状态

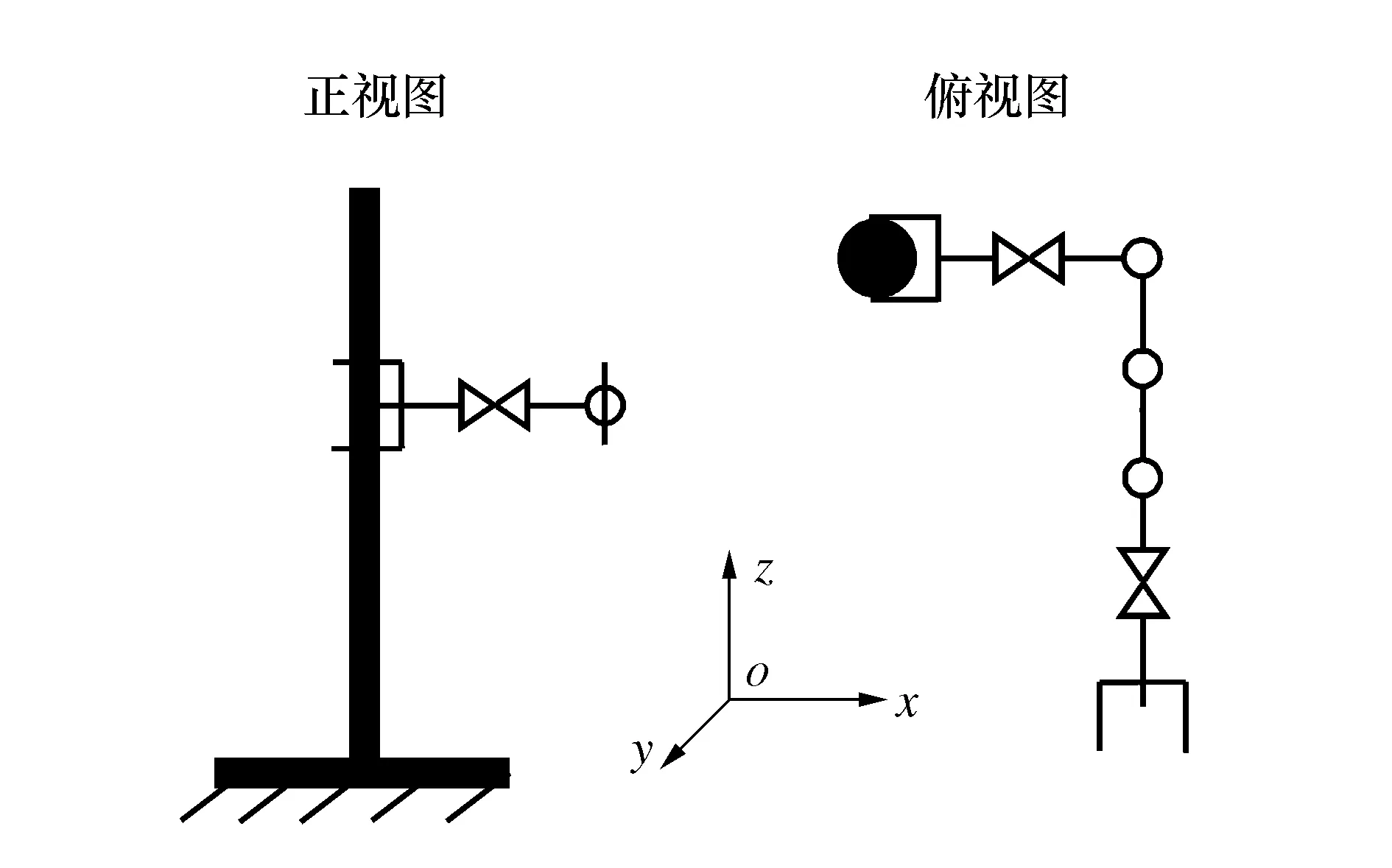
图9 机器人空间攀爬最大负载状态

为了探究夹持机构在以上两种负载形式下的负载能力,本文采用ANSYS对夹持机构进行负载仿真,将SolidWorks夹持机构模型导入ANSYS Workbench中,设置夹持机构材料为7075铝合金,设置管道为钢材,设置夹持机构与管道接触零件为橡胶,并设置接触与约束、划分网格。得到夹持机构仿真环境如图10所示。

夹持机构电机向滑台可提供的最大推力约为2 000 N。对夹持机构进行瞬态分析仿真,仿真分2步进行,第1步模拟传动装置给滑台施加2 000 N固定推力,使夹持机构夹紧管道,第2步在夹持机构末端施加等效负载。以下分别进行z轴负方向力负载仿真(以下简称力负载仿真)和x轴方向力矩负载仿真(以下简称力矩负载仿真)。

1)力负载仿真

力负载仿真负载具体添加方式如表2所示。

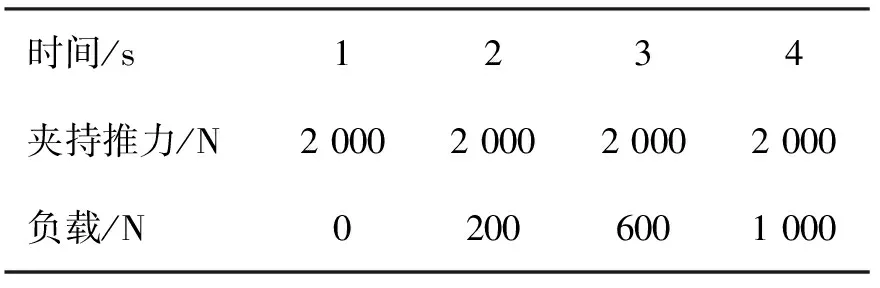
表2 力负载仿真的输入负载

仿真得到夹持机构最大位移时间曲线图如图11所示。

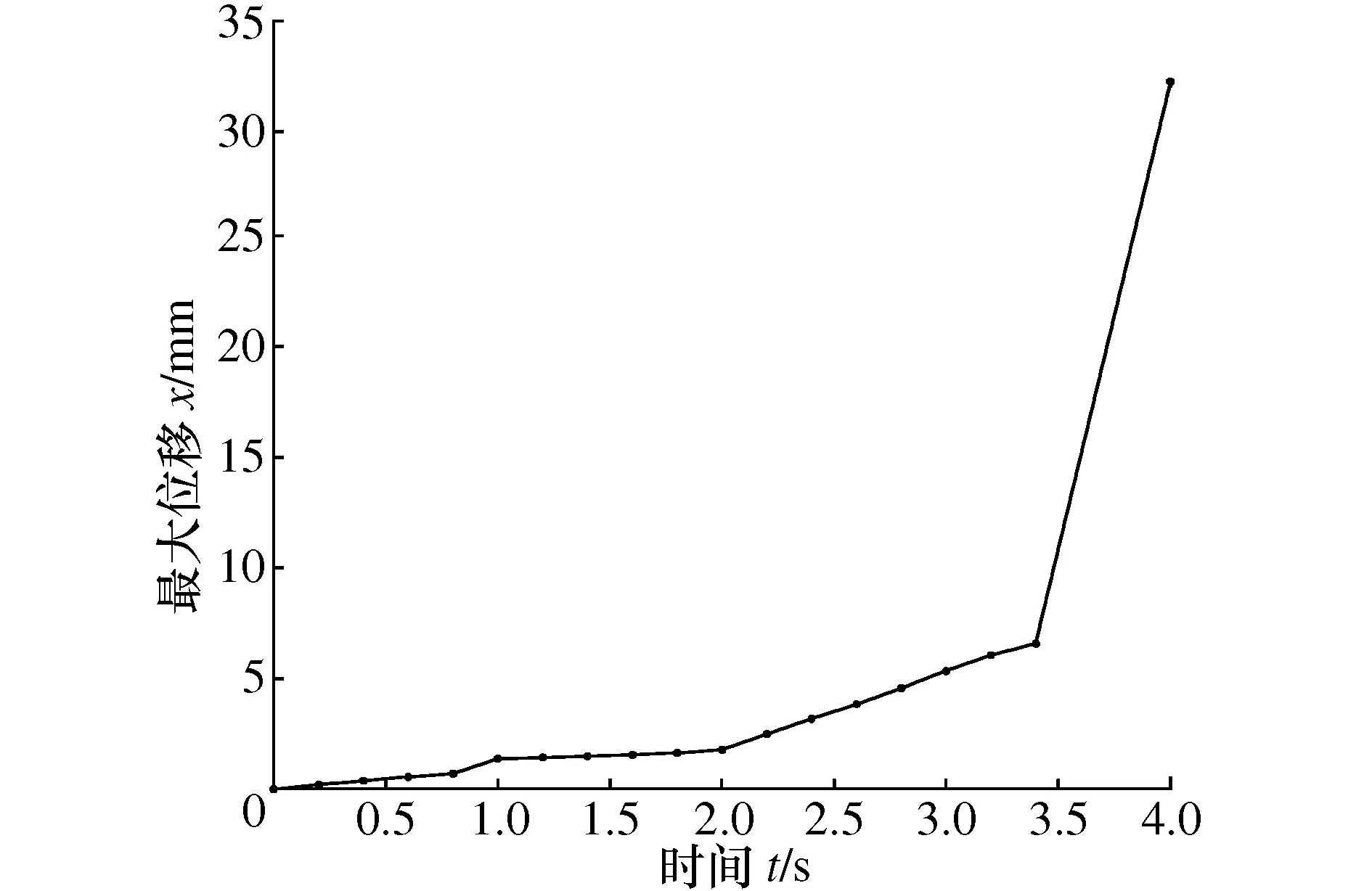
图11 力负载仿真最大位移时间曲线

由图11可得,在3.4 s之后,位移曲线大幅增加,此时夹持机构脱落,仿真无法继续进行。因此夹持机构末端所能承受的最大的力负载约为800 N。

2)力矩负载仿真

力矩负载仿真负载具体添加方式如表3所示。

表3 力矩负载仿真的输入负载

仿真得到夹持机构位移时间曲线图如图12所示。

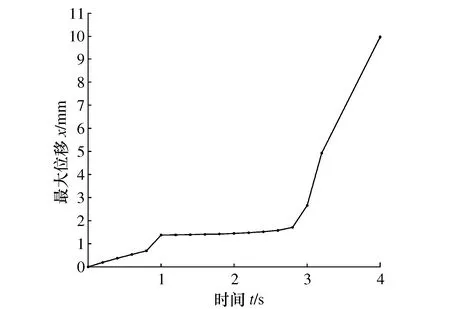
图12 空间负载仿真的位移时间曲线

由图12可得,在3.2 s时,位移曲线大幅增加,夹持机构已无法夹紧,仿真无法继续,因此夹持机构x轴方向最大负载力矩约为22.5 Nm。

仿真结果表明该夹持机构在夹持机构末端所能承受的沿z轴负方向最大的力负载约为800 N,沿x轴方向的最大力矩负载约为22.5 Nm。

3.2 样机试验

为了验证该夹持机构的可靠性,本文采用5自由度管道攀爬机器人做运动负载试验。该机器人主要应用在电厂密集管道环境中,需要完成单根管道攀爬作业和管道间跨越作业,对应两种常用的步态,如图13和图14所示。

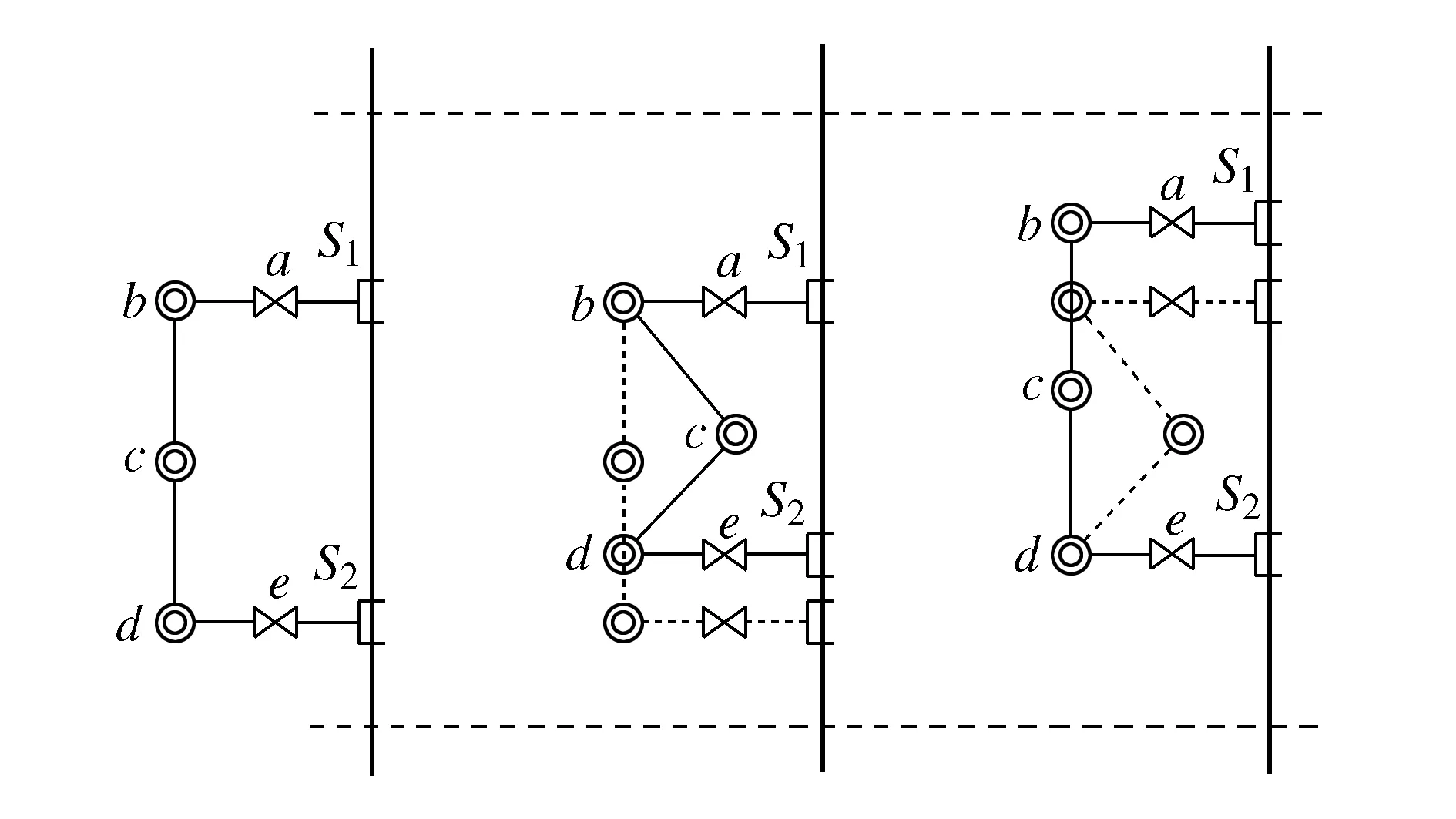
图13 直管攀爬步态

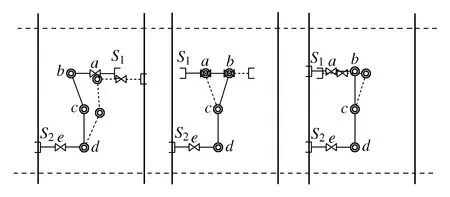
图14 管间跨越步态

以这两种步态进行机器人负载试验,如图15所示。试验中的机器人自重3.6 kg,总长为712 mm,夹持机构重量为431 g。

图15 机器人运动负载试验

以上试验分别进行30次,试验结果如表4所示。

表4 机器人运动负载试验结果

由表4可以看出机器人在直管攀爬步态下夹持机构能稳定可靠夹持;在管间跨越步态下夹持机构有一次失败,失败的原因主要是机器人运动采用离线规划的形式,机器人关节间隙较大,导致夹持机构末端与管道位置相差较大,造成夹持失败,但在成功状态下,夹持机构都能稳定夹持。

4 结论

1)针对夹持式管道攀爬机器人设计了一种夹持机构,该夹持机构采用三线夹持方式,具有良好的自定心功能。

2)进行连杆机构优化,夹持机构重量相对于优化前减少11.7%,提高了夹持机构的负载能力。

3)对夹持机构进行仿真分析得到其理论负载能力,沿z轴负方向的最大力负载为800 N,沿x轴的最大力矩负载22.5 Nm;进行机器人负载试验,证明了该夹持机构的可靠性。