双叶片半转叶轮水轮机水动力性能实验研究

王孝义,李磊,孙承坤,于晓峰,刘聪,张玉华

(安徽工业大学 机械工程学院,安徽马鞍山 243002)

潮流能作为一种能量密度高、存储量大的清洁可再生能源,已经逐渐成为国内外研究热点[1]。垂直轴水轮机作为一种潮流能转换装置因其便于维护,结构简单等特点受到人们越来越多的关注[2]。

垂直轴水轮机研究主要围绕Savonius叶轮阻力型水轮机和Darrieus叶轮升力型水轮机展开[3-4]。各国研究者探究了叶片形状[5]、密实度[6]、叶轮转臂[7]、高柔性叶片[8]等参数对水轮机水动力性能的影响规律。目前研究结果表明,升力型垂直轴水轮机具有较高的获能效率,一般可达35%左右[9],但是其启动性能差,尤其是低流速水流下启动性能更差;阻力型垂直轴水轮机低流速下具有良好的启动性能,但是其获能效率较低,水下实验仅为20%左右[10]。我国潮流能储能丰富,但大多数流域流速较低[11],难以满足高获能效率型水轮机启动流速要求,而低流速下可运行水轮机获能效率不高[12]。因此设计一款低流速下获能效率高的水轮机具有重要的现实意义。

半转机构[13]是安徽工业大学仿生研究团队研发的一种能实现不对称运动的新型机构。在将半转机构应用于仿生飞行和水下推进中发现,采用该机构设计的装置与流体介质之间相互运动时表现出良好的流体动力性能[14-15],遂将其引入潮流能发电领域,设计出一种升阻复合新型垂直轴水轮机——半转叶轮水轮机。通过数值模拟研究发现,半转叶轮水轮机不但具有良好的低流速自启性能,而且获能效率高于传统升力型垂直轴水轮机。为了获取半转叶轮水轮机水下实际的水动力性能,本文在设计制造出双叶片水轮机实验样机的基础上,搭建了水下实验平台,进行半转叶轮水轮机水动力性能测试,以验证前期数值模拟的可靠性,检验新型水轮机优缺点,为后期改进设计和实际应用提供有效支撑。

1 双叶片半转叶轮水轮机工作原理及其实验样机

图1为半转机构运行原理图,其中动轮直径为定轮的两倍,半转构件与动轮固连。当系杆以角速度ω转动时,半转构件以角速度ω/2转动,且两者方向相同。进而实现系杆转动一圈,半转构件转动半圈的运动效果,将该运动机构称为半转机构。

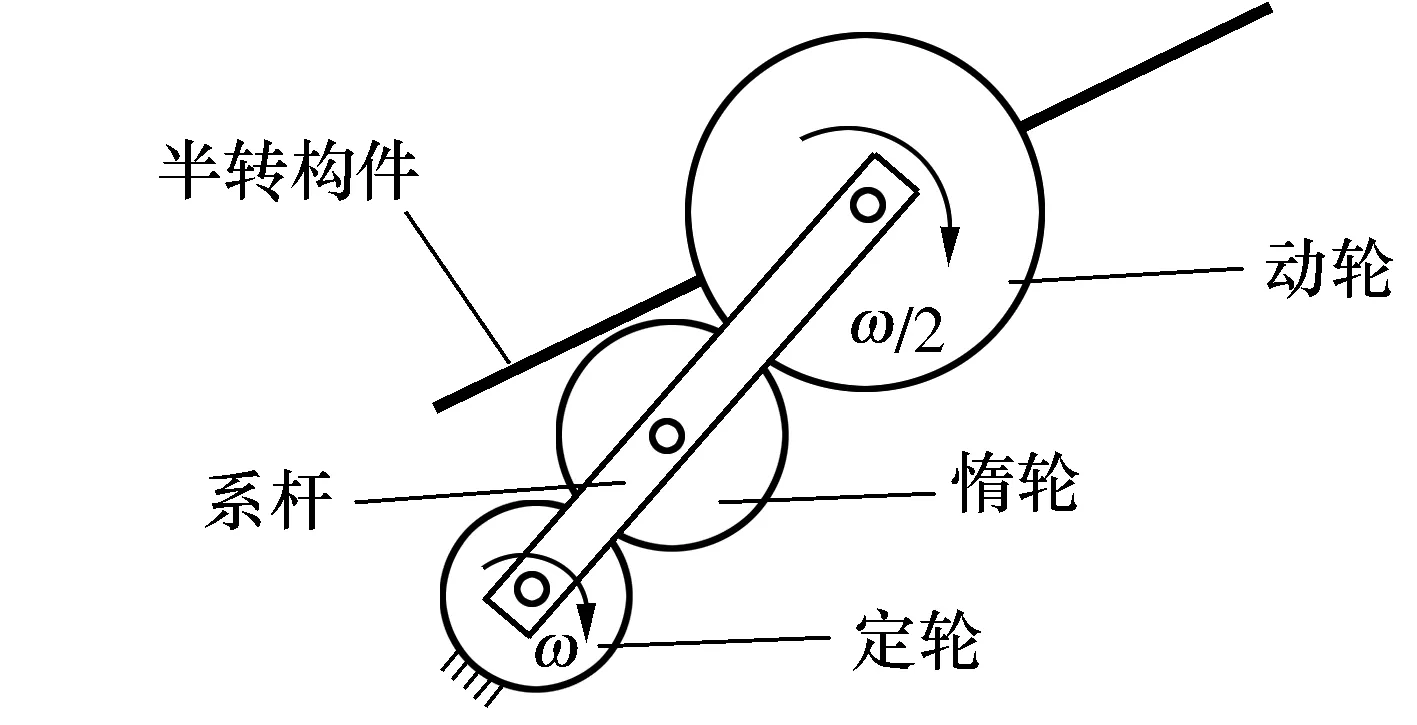
图1 半转机构运行原理

将半转机构应用于潮流能发电领域,系杆对称演化为转臂,半转构件演化为叶片,衍生设计双叶片半转叶轮水轮机(以下简称水轮机)如图2a)所示,其中定轮与机架固连,输出轴与上转臂固连,定轮与动轮之间采用惰轮过渡。为提高叶片运行稳定性和强度,转臂选用上下布置的形式。

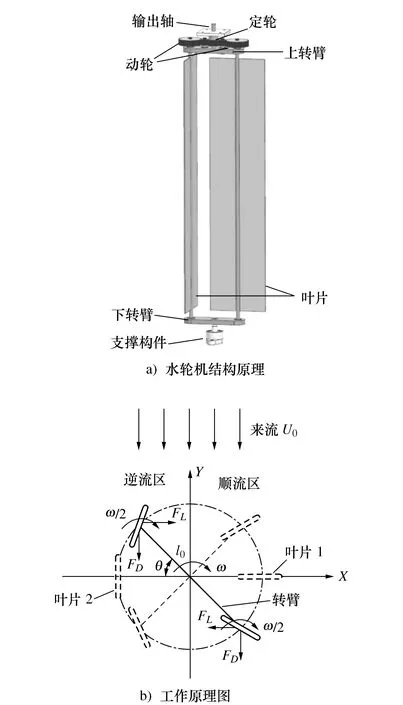
图2 水轮机结构及其工作原理

如图2b)所示,当来流以速度U0沿着Y轴负方向流向水轮机时,来流作用于叶片会同时产生阻力FD和绕流升力FL。将水轮机叶片运行区域按照叶片转动与来流的相对方向分为逆流区和顺流区。在顺流区叶片与来流攻角较大,水轮机受力以阻力为主;在逆流区叶片与来流攻角较小,水轮机受力以升力为主。叶片在不同区域的受力特点表明半转叶轮水轮机有机融合了升力和阻力两种特性,因此半转叶轮水轮机实质上是一种新型的升阻复合水轮机。通过加装偏航对流装置可以消除不同来流方向对半转叶轮水轮机获能性能的影响。

选取叶轮结构参数制造实验样机,转臂长度l0=0.085 m,叶片展长C=0.9 m,叶片弦长L=0.2 m,并制造出双叶片半转叶轮水轮机样机如图3所示。水轮机主要由转臂、叶片、输出轴、传动齿轮和机架等组成。转臂与输出轴固连,可绕输出轴中心轴线转动,叶片1和叶片2相互垂直并分通过轴承连接于转臂两端。

图3 水轮机实验样机

如图2b)所示,本文实验中水轮机叶片初始相位为来流正对叶片,来流方向与叶片1垂直、与叶片2平行。当来流以速度U0沿Y轴负方向流向半转叶轮水轮机,叶片吸收潮流能形成动力转矩带动转臂转动同时实现叶片自转。

2 水轮机水动力性能参数及其实验方案

2.1 性能参数与分析

水轮机的输出功率和获能效率从不同视角表征水轮机水动力性能的优劣。

1)输出功率和输入功率

输出功率P为单位时间内水轮机实际捕获一定流速水介质的能量，即

(1)

式中:n为输出轴转速,r/min;M为输出转矩,Nm。

输入功率P0为单位时间内水介质以流速U0流向水轮机叶轮扫掠面积S(即叶轮工作区域面积)时可以产生的理论能量，即

(2)

2)获能效率Cp

获能效率Cp为输出功率与输入功率的比值,其数值大小表示水轮机能量转换性能的强弱,联立式(1)与式(2)得

(3)

另一方面,根据半转叶片端点轨迹[16],则水轮机叶轮扫掠面积S为

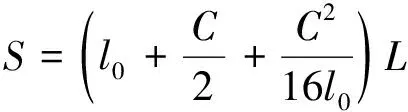
(4)

式中:l0为水轮机转臂长度,m;C为叶片弦长,m;L为叶片展长,m。

需要指出的是,水轮机实际运行过程中,瞬时输出转矩和转速是变化的,因而瞬时获能效率也是变化的。由于水轮机叶片运动的周期性,本文采用平均获能效率综合评判水轮机的能量捕获与转换能力。平均获能效率为水轮机平稳运行时若干周期内输出功率与输入功率的比值。计算平均获能效率时,式(3)中的输出转矩M和转速n均采用周期平均值。如无特殊说明,下文中获能效率均指平均获能效率。

2.2 实验方案

为了综合测试水轮机水动力性能,本实验主要围绕以下3个测试重点展开:

1)水轮机低速自启性能测试

在0.5 m/s来流速度及低值定负载下,测试并观察水轮机从静止到稳定运行阶段的转速变化情况。

2)水轮机获能效率测试

水轮机空载稳定运行后,从0开始逐渐增加水轮机外部负载,直至水轮机停转,测试并观察水轮机在不同流速、不同负载转矩下的转速变化情况,从而获得不同流速下水轮机获能效率分布规律。

3)水轮机获能效率稳定性测试

在水轮机运行平稳阶段,测试水轮机处于最佳获能状态(获能效率最高)时的瞬时获能效率随时间变化情况。

上述测试需要通过合适的实验平台实时获取水流流速U0、水轮机输出转矩M和转速n等实验参数。

3 实验平台设计

图4所示的实验平台采用“水静船进”的方式模拟来流对水轮机的作用。水轮机样机固定安装在浮筒式实验船中轴线的船体前端,能够实现来流方向正对叶片。采用无级变速推进器推动实验船前进,实现不同来流速度下水轮机水动力性能测试。实验测控系统与水轮机输出轴相连,实时测量并记录水轮机实验过程中运转参数变化。为排除外界波浪干扰,实验选择在无风浪的开阔平静水域进行。

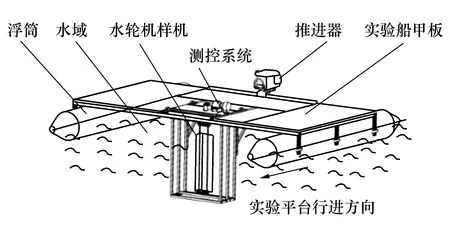
图4 水轮机实验测试平台示意图

值得一提的是,将水轮机前置固定安装于实验平台中心轴线上,保证了来流方向始终与水轮机垂直,消除了不同来流方向对半转叶轮水轮机获能性能的影响,因而图3中的水轮机样机未添加偏航对流装置。同时对船体进行加宽处理,避免船体扰动来流对水轮机运行产生影响。

为防止来流速度增大引起实验平台出现俯仰(相当于水轮机实际浮台的纵摇)运动,进而降低水轮机的获能效率,必须正确选择推进器螺旋桨的放置深度。如图5所示,以实验平台中心为原点O,来流方向作为X轴正方向,建立简化的实验平台俯仰运动分析模型。

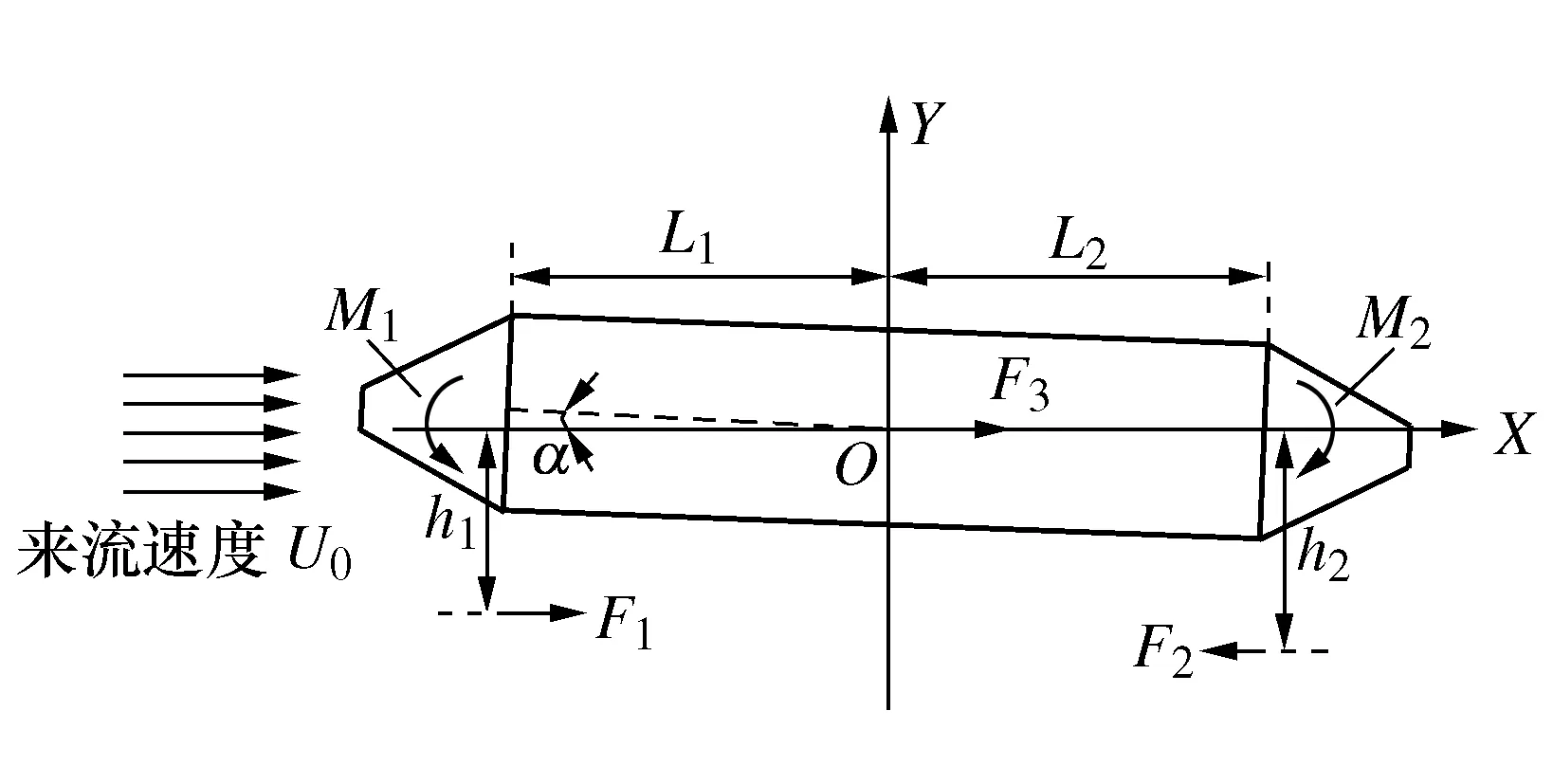
图5 实验平台俯仰运动分析模型

图5中：F1为来流对水轮机的阻力；F2为推进器螺旋桨推力；F3为来流对实验平台的阻力；h1为水轮机安装深度；h2为推进器螺旋桨安装深度;L1为水轮机与实验平台水平距离；L2为推进器与实验平台水平距离。实验平台设计与制造时取L1=L2。实验过程中,F1产生的阻抗力矩M1与F2产生的推进力矩M2相互作用,当M1与M2不能完全抵消时将产生一定的俯仰角度α。俯仰角的形成又将导致不均匀浮力及其力矩的生成,进而抑制俯仰角的增大。经测算并兼顾推进器实际轴长,选取推进器螺旋桨放置深度h2=0.35 m。多次实验表明该深度能够保证不同来流速度下,实验平台保持基本水平。

最终搭建实验测试平台及其实验现场如图6所示。

图6 水下实验现场图

实验通过调节磁粉加载器控制负载(负载即为输出转矩)大小,采用多普勒测速仪与扭矩转速传感器实时采集三维流速、输出转矩和转速等参数数据。为保证采集数据稳定可靠,流速仪采样频率与转矩转速传感器采样频率设置为15 Hz,单次采样有效时间大于15 s。

4 实验数据处理与结果分析

实验平台运行过程不可避免地存在微幅振动,实测来流速度随之小幅波动,因此流速计算时选取实验船稳定运行时间段的流速数据,并采用中心过滤法对实测流速数据进行处理。根据实验采集的负载转矩、转速和来流速度等参数数据以及水轮机结构参数,通过式(1)～式(3)计算得出水轮机在该时间段内的各项水动力性能参数。

4.1 水轮机低速自启性能分析

图7为水轮机在加载0.4 Nm负载、来流速度为0.5 m/s工况下自启过程中转速变化规律。由图7可见,水轮机启动过程主要分3个阶段:初始急加速阶段、缓加速阶段和稳定运行阶段。水轮机在0～4 s处于初始急加速阶段,水轮机在来流作用从静止开始转动,转速从0开始呈现快速增长;4～8 s由于水轮机转速增加,水轮机所受阻力做功增大,但来流对水轮机依旧做有效功,水轮机进入缓加速状态,水轮机转速保持缓慢增长状态;8 s之后水轮机已经处于当前负载最大转速,处于完全启动状态,开始稳定运行。

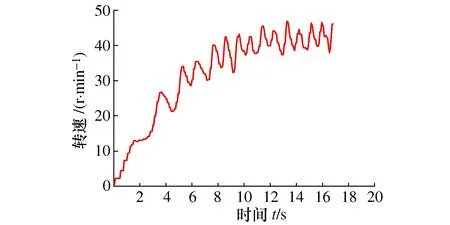
图7 启动过程转速变化规律

4.2 水轮机获能效率分析

4.2.1 实验结果分析

表1～表3列出了实测来流速度分别为0.50 m/s、0.75 m/s和1.00 m/s时水轮机在不同负载下运行状态参数及其性能表现。由于来流速度无法实现完全恒定,因此表中实测流速数据有波动。

表1 0.50 m/s来流速度下水轮机运行状态

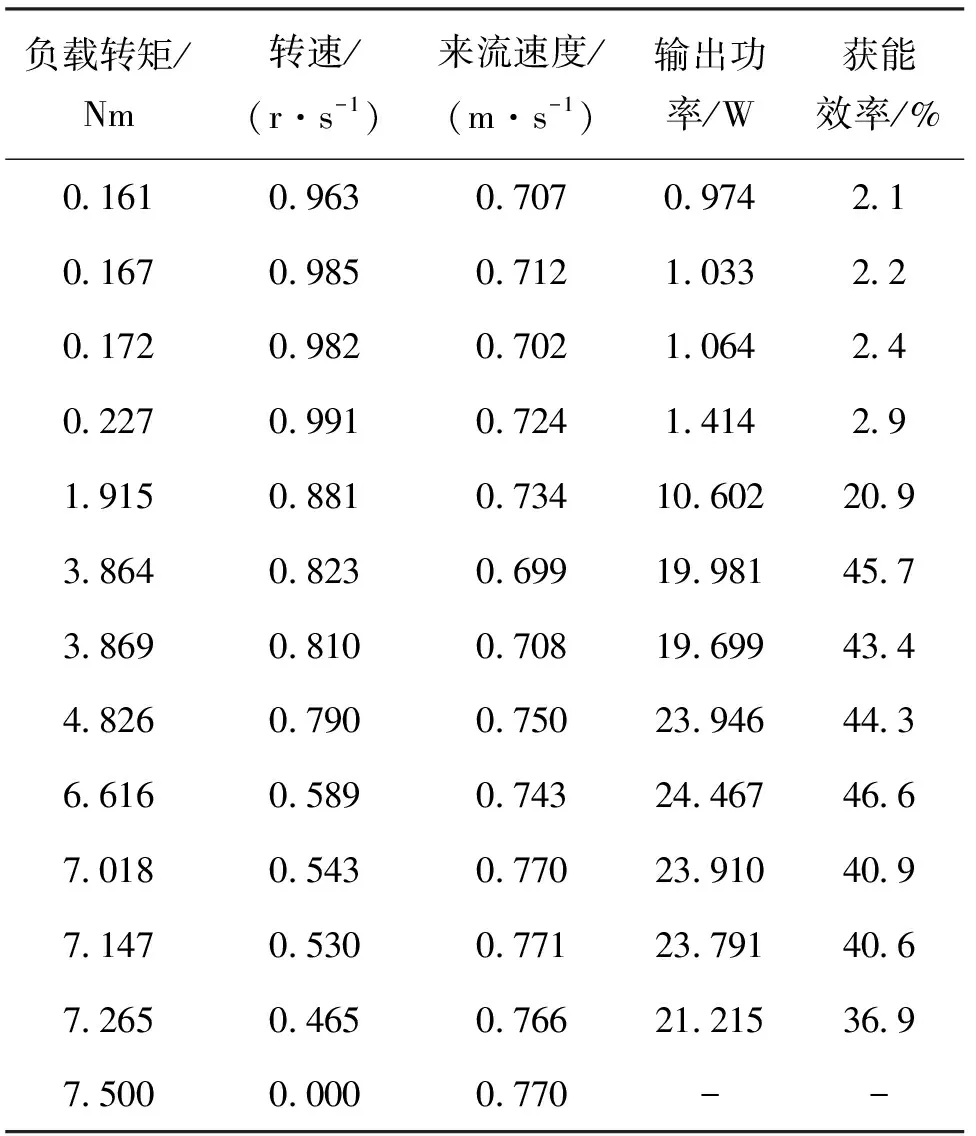
表2 0.75 m/s来流速度下水轮机运行状态

表3 1.00 m/s来流速度下水轮机运行状态

图8为对应表1～表3中水轮机在不同流速下平均获能效率变化规律图。双叶片半转叶轮水轮机获能效率随负载缓慢增大,到达极值后,稍微增加负载水轮机获能效率即开始快速下降。不同来流速度条件下,通过调节负载转矩,水轮机最大获能效率均可达到46%。与同类垂直轴水轮机获能效率相比,最大获能效率提高了43%[12]。

图8 获能效率随负载变化规律

4.2.2 水下实验与数值模拟结果比较

除水下实验外,本文还用CFD方法对水轮机水动力性能进行了数值模拟,并对文献[16]的分析模型进行了改进,流动模型使用自由面流的水道流,从而与水轮机实际工况更相符。图9为双叶片半转叶轮水轮机在不同来流速度下的数值模拟与实验的获能效率曲线对比。由图9可见,水下实验与数值模拟数据的变化趋势基本一致,均为随着转矩的增加效率先增后减。但由于实验样机存在摩擦以及传动效率的损失,水下实验的获能效率小于数值模拟的获能效率。另外,水下实验中,当负载阻尼稍大于启动转矩时,水轮机叶轮立即停转;因此,水下试验中获能效率到达峰值点后随转矩的增加效率急剧下降。总体来说,水下实验与数值模拟的吻合效果较好。数值模拟结果与水下实验结果均表明来流速度对双叶片半转叶轮水轮机最大获能效率影响较小。

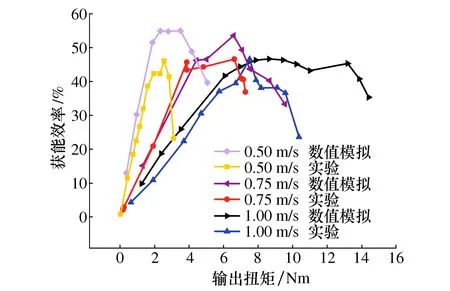
图9 实验-数值模拟对比

需要强调的是,水下实验与数值模拟结果均表明,对于双叶片半转叶轮水轮机而言,每种来流速度都对应一种最佳负载,使得水轮机获能效率达到最大值,本文称这种流速-负载组合为水轮机最佳获能状态。最佳负载小于极限负载,不会导致水轮机停机。数值模拟能够有效的寻找水轮机实际运行过程中最佳获能状态区间,用以指导水轮机高效工作。因此在水轮机实际使用中,应当根据来流速度自适应地将负载调至最佳负载,以使水轮机始终处于最佳获能状态。

4.3 水轮机获能效率稳定性分析

水轮机工作时,不仅需要有较高的平均获能效率,还应该具有能量输出稳定性。如2.2节所述,水轮机实际运行过程中,其瞬时输出转矩和转速是变化的,导致瞬时获能效率随之变化。

以1.00 m/s来流速度实验为例,7.505 Nm为最佳负载(见表3),可以获得46%的平均获能效率。为深入探究1.00 m/s-7.505 Nm水轮机最佳获能状态下瞬时获能效率变化情况,取水轮机稳定运行阶段单个周期内的采集数据,以单个测量点数据计算其瞬时获能效率并绘制瞬时获能效率变化规律，如图10所示。由图10可知,水轮机在一个运行周期内其获能效率会产生一定的波动。

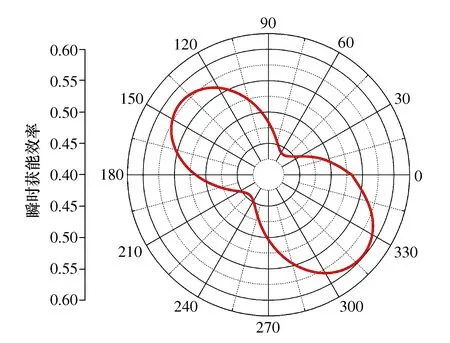
图10 水轮机获能效率变化规律

上述结果表明,半转叶轮水轮机在发电领域虽然平均获能性能有着较为优良的表现,但其瞬时获能效率呈周期性变化,能量输出稳定性还有一定的提升空间。尚需通过进一步改进水轮机结构来改善能量输出质量。

5 结论

双叶片半转叶轮水轮机实质上是一种新型升阻复合型水轮机。本文通过一定的实验平台和实验方案,开展了实验样机的水下实验,结果表明:

1)水轮机在低流速下保持良好的启动特性。启动过程经历急加速阶段、缓加速阶段,达到相应负载下最大转速后进入启动稳定运转阶段。

2)来流速度对水轮机获能效率影响较小。每种来流速度都对应一种最佳负载,使得水轮机获能效率达到最大值;最佳负载下水轮机获能效率可达46%,比同类垂直轴水轮机获能效率提高43%。

3)水轮机在稳定运行阶段,瞬时获能效率呈现周期性变化,双叶片半转叶轮水轮机能量输出稳定性还需提高。

目前,课题组正在探索改变半转叶轮水轮机的叶片数目和翼型来改善能量输出稳定性,并取得了初步效果。