稀疏网格模型在变速箱壳体轻量化设计中的应用

刘爽,吉效科,张思,华剑*，

(1.长江大学 机械工程学院,湖北荆州 434023; 2.长庆油田公司 机械制造总厂,西安 710018)

2021年以来,全球出现原材料涨价潮,国内原材料也相应大幅上涨,这给国内制造业带来了很大的压力[1]。因此以降本增益为目标,对变速箱设计提出的新要求是轻量化设计,而变速箱壳体轻量化设计则是其重要组成部分[2]。在传统经验设计中,人们设计所得的尺寸太过保守,过度地加大了壳体的壁厚,致使壳体质量增加,造成了材料的浪费。因此在满足强度、刚度的要求下设计出质量最轻的壳体结构就显得十分关键。深化变速箱壳体的轻量化技术研究,对于节约成本,提升效益有着深远的意义。

针对变速箱的轻量化设计问题,国内外学者采用了变密度法、响应面优化法、静动态联合拓扑优化等方法,均取得了较好的效果。Degtyarev等[3]对运载火箭的waffle壳截面进行参数优化,使其厚度减小,减轻了壳体质量;王海林等[4]对拖拉机变速器箱体进行动态特性分析及优化设计,质量减少8.7%,前6阶固有频率都得到提高;李永华等[5]采用最小二乘法构建响应面模型,在提高蓄电池箱共振可靠性的同时减轻了结构质量;杨岳等[6]对水下机器人耐压壳体进行了结构优化,使耐压壳体质量降低15.52%。诸多学者采用其方法均取得不错效果,但分析发现针对压裂泵用变速箱壳体的轻量化研究则很少。

本文分别研究了稀疏网格模型与常用近似模型预测精度问题,提出了一种稀疏网格模型与MOGA算法相结合的优化方法,在有限元分析软件提供的协同仿真环境下,完成了壳体的参数化建模和轻量化设计。最终在保证结构性能满足要求的情况下使壳体质量降低了18.1%,提高了材料的利用率。

1 近似模型研究

在复杂工程系统的设计优化中,由于设计变量和优化目标繁多,分析中存在计算量大和优化效率低等难题。为高效地进行设计优化,往往会引入近似模型,在提升优化效率和计算速度的同时也牺牲了一定精度,而常用近似模型在预测精度方面存在着差异。因此,以碟簧为背景,对常用近似模型与稀疏网格近似模型的预测精度进行对比研究。图1为碟簧示意图。

图1 碟簧示意图

以P3、P4为设计变量，最大变形为优化目标构建少极值、少变量情况,各近似模型预测精度如表1所示。

表1 碟簧单目标预测平均绝对百分比误差(MAPE) %

MAPE是用于评估预测性能的指标,使用百分率来衡量偏离的大小,MAPE越小,说明模型质量越好。由表1可知,多项式、Kriging和稀疏网格方法在处理低纬度问题时均有不错的预测精度。但对比发现,稀疏网格模型中平均绝对百分比误差值最小,由此可见稀疏网格模型在少极值,少变量情况更具优势。

图2为各近似模型预测值与实际值分布图,样本点响应值越接近等值线(y=x),表明预测模型准确性越高。

图2 预测值与实际值分布图

由图2可知,多项式响应面模型不适用于高纬度、多极值、多变量问题,在此情况下其预测值与实际值相差较大,模型精度较低;Kriging模型样本点预测精度较高,但插入验证点求解发现预测值与实际值存在差距;稀疏网格模型不仅样本点预测精度较高,而且验证点的预测值接近实际值,表明其预测精度较高。以P1、P2、P3、P4为设计变量;质量、最大变形、最大等效应力为优化目标构建高纬度、多极值、多变量情况,各近似模型预测精度如表2所示。

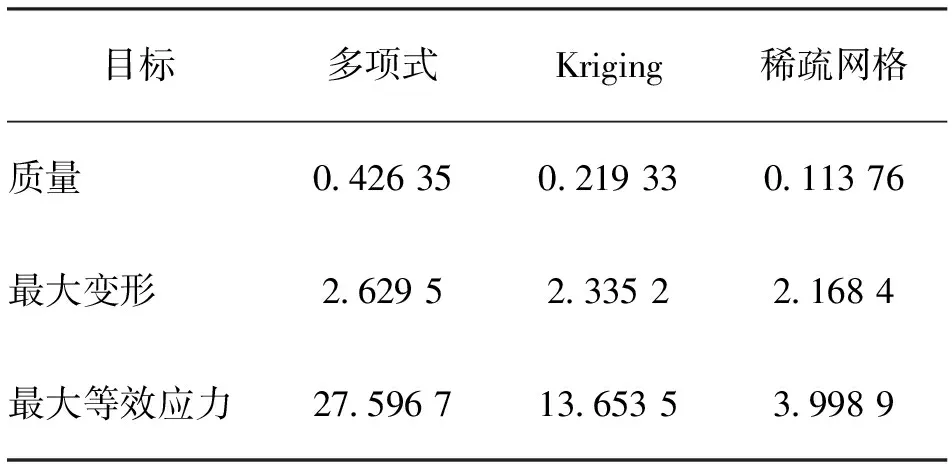
表2 碟簧多目标预测平均绝对百分比误差(MAPE) %

稀疏网格模型在质量、最大变形、最大等效应力的平均绝对百分比误差均为3者中最小,表明其模型预测值误差最小,模型质量最高。

稀疏网格模型在构建少极值、少变量问题及多极值、多变量问题时预测精度均优于其他两种近似模型。本文将基于稀疏网格模型对变速箱壳体展开轻量化设计。

2 变速箱壳体模型分析

2.1 几何模型

壳体为左右对称式结构,大半圆为输入轴轴承座,小半圆为输出轴轴承座,壁厚和4根加强筋用来支撑载荷。采用三维软件进行建模,几何模型如图3所示。

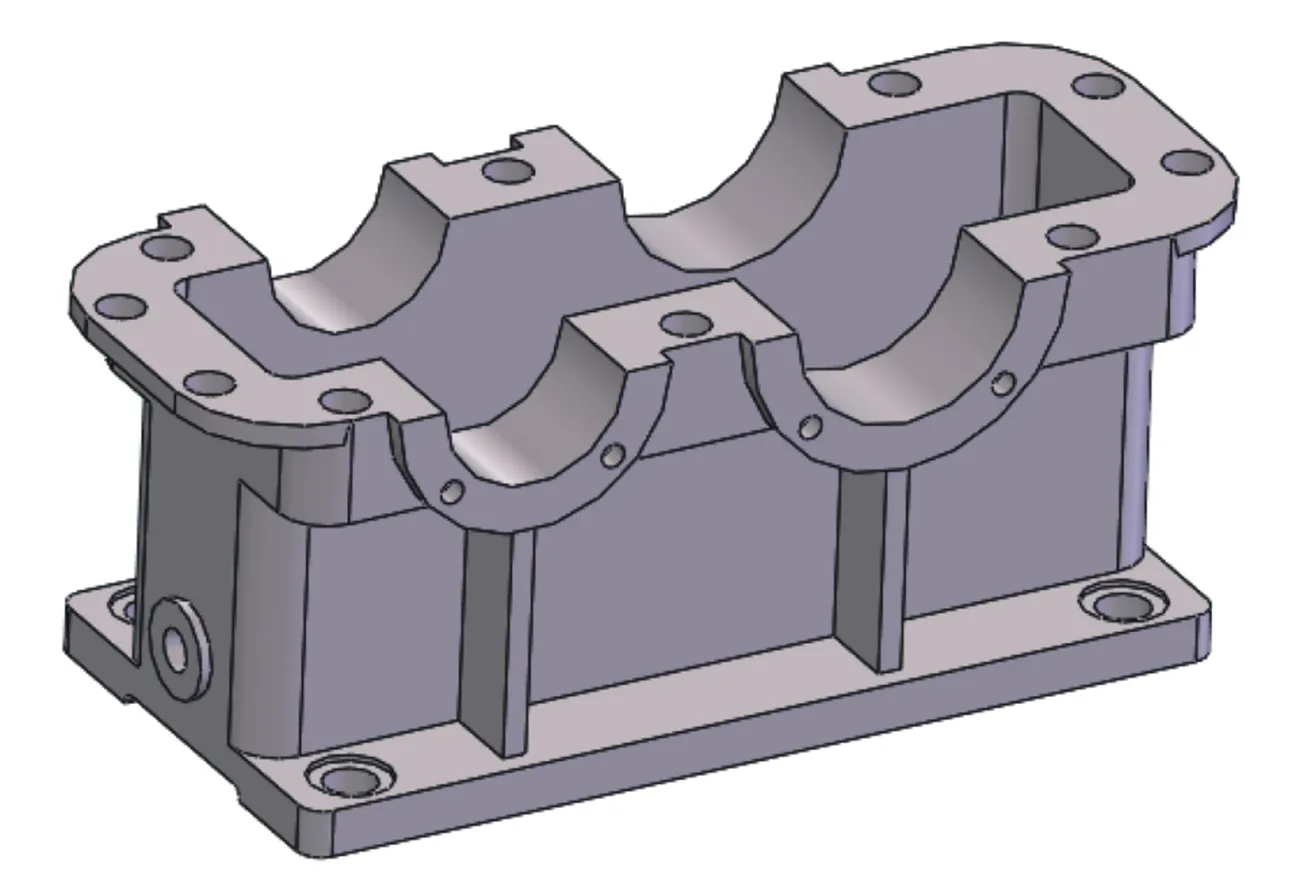
图3 变速箱壳体几何模型

考虑后续有限元分分析计算量较大,对壳体结构进行以下简化,以降低优化复杂性:

1)去除不影响结构强度,刚度的凸台和孔等;

2)忽略壳体上各种尺寸的圆角、倒角,防止引起网格密集,花费大量时间。

采用自动划分网格方法,网格尺寸为5 mm,划分网格后壳体模型节点个数为397 697,单元个数为229 565,网格平均质量为0.82,网格质量良好。壳体的网格模型如图4所示,壳体的材料属性如表3所示。

表3 HT200壳体材料属性

图4 变速箱壳体网格模型

2.2 壳体静态特性分析

变速器工作时,箱座除了承受上箱体的重力载荷外还要承受的工作载荷,轴承与轴承座以相互接触的方式来传递工作载荷。在齿轮工作过程中,法向载荷Fn垂直于齿面,将Fn沿齿轮的周向、径向及轴向分解成3个垂直的力,其大小分别为:

(1)

式中:F1为周向力;F2为径向力;F3为轴向力;T1为转矩;d为节圆直径;αn为法向压力角;β为节圆螺旋角。

轴承座为载荷主要作用区域,载荷沿轴承座的圆周分布力可以表示为

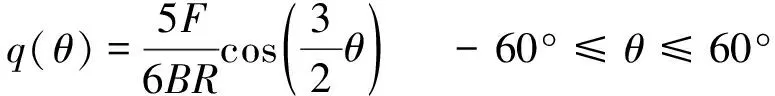
(2)

轴承载荷分布如图5所示。轴承工作挤压时会产生变形,所以周向轴承并不是180°,而是按照周向120°的区域承载来模拟轴承的工作情况,载荷在120°范围内可假定按余弦函数分布[7]。壳体被底座上的螺钉完全固定,静力分析时对底座进行完全约束。

图5 轴承载荷分布

通过计算取整得到大半圆面的轴向力为3 230 N,小半圆面的轴向力为2 750 N,壳体上表面承受来自上箱体的重力,上箱体的质量约为303.4 kg,计算得到重力为2 973 N的力,图6为壳体载荷约束图。

图6 壳体载荷约束图

在有限元分析软件Workbench设置载荷及约束计算求解,得到壳体的变形云图如图7所示,等效应力云图如图8所示。

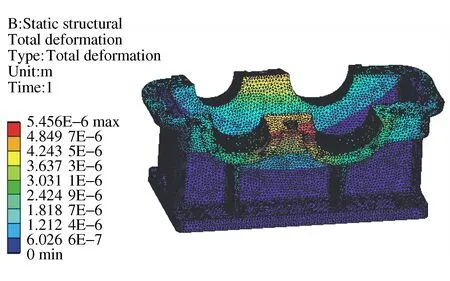
图7 壳体变形云图

图8 壳体等效应力云图

由图7和图8可知,壳体变形主要发生在与变速箱上壳体接触位置的中部,最大变形值为0.005 6 mm;壳体应力主要集中输入轴轴承座的两侧加强筋处,最大等效应力为1.9 MPa,远低于材料的极限强度200 MPa,对壳体结构影响较小。

由此可见,在传统设计中,为了满足强度与刚度,壳体的壁厚常常被过度地增加,致使结构主体应力水平较低,材料性能没有充分发挥,有进一步轻量化设计的空间。

2.3 壳体动态特性分析

对壳体底座施加约束进行模态分析,根据振动理论得知,低阶模态最能展现结构的动态特性。因此提取壳体前6阶的固有频率与振型数据如表4所示。

表4 壳体前6阶固有频率及振型

由表4可知,壳体约束后前6阶模态中最低阶模态频率为394.28 Hz,最高阶模态频率为938.88 Hz,振型主要表现为整体振动变形,壳体振动明显的部位主要集中在壳体上端中部两侧以及前后两侧。

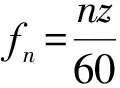
3 优化分析过程

3.1 优化流程图

以最小质量为最优优化目标进行参数设计。主要步骤包括:有限元模型建立与分析、灵敏度分析确定设计变量、基于稀疏网格模型理论构建近似模型建、利用多目标遗传算法MOGA算法搜索以及获取最优设计方案，详细流程如图9所示。

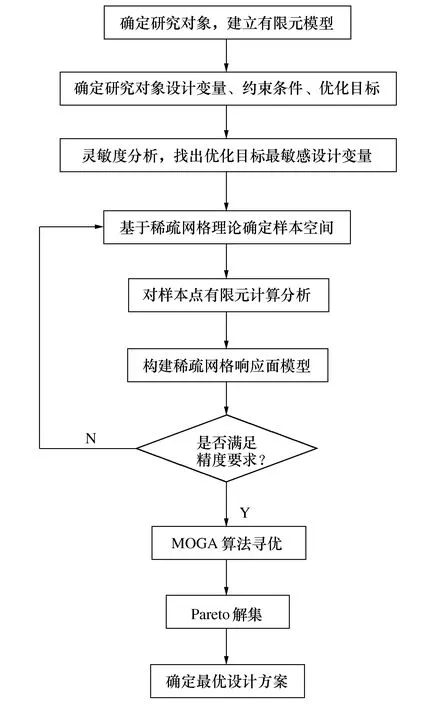
图9 优化分析流程图

3.2 壳体设计变量

在确保壳体形状不发生改变,仅改变厚度的前提下,选取P1为壳体中部两侧壁厚;P2为壳体前壁厚;P3为壳体后壁厚;P4为壳体中部深度;P5为底板厚度;P6为4根筋宽度和P7为4根筋的长度作为设计变量,如图10所示。设计变量均以初始值的±30%来设置上下限,如表5所示。

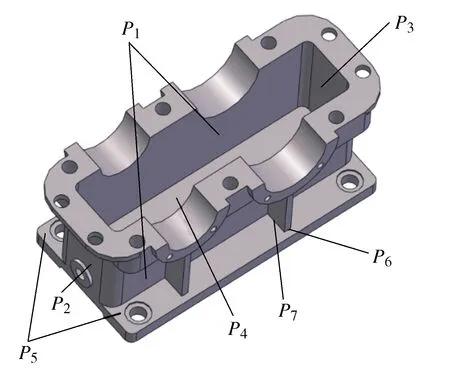
图10 设计变量示意图

表5 壳体设计变量上下限

3.3 设计变量灵敏度分析

灵敏度分析方法可反映设计变量对目标函数影响的变化梯度,通过该法可分析出各个设计变量对于目标函数贡献程度及敏感性参数值[9]。灵敏度的思想穿插于众多学科中,在各领域中均有涉及。

连续可导的设计变量(x1,x2,…,xn)用函数表示为

F(x)=F(x1,x2,…,xn)

(3)

F(x)对应的1阶灵敏度用函数表示为

(4)

高阶微分灵敏度及高阶差分灵敏度可以表示为

(5)

(6)

灵敏度S可以表示为

(7)

变速箱壳体的7个尺寸参数对输出变量的灵敏度如图11所示。

图11 灵敏度分析图

灵敏度为正值表示优化目标与设计变量成正相关,即各优化目标随变量数值的增大而增大,负值表示优化目标与设计变量成负相关,即各优化目标随变量数值的增大而减小[10]。由图11可知：P1、P5对质量的影响最大;P1、P7对最大变形的影响最大;P1、P6对最大等效应力的影响最大;P1、P7对1阶固有频率的影响最大。因此选择对质量P8、最大变形P9、最大等效应力P10和1阶固有频率P11影响最大的尺寸参数P1、P5、P6、P7作为设计变量。

3.4 优化目标模型

轻量化目标是进一步地减轻壳体的质量,同时还要确保壳体具有足够的强度、刚度。将通过灵敏度分析筛选出的4个设计变量(P1、P5、P6、P7)表示为

X=[P1,P5,P6,P7]T

(8)

由此可知目标函数表示为:

(9)

以最轻质量、最小总体变形、最大等效应力小于200 MPa,最大1阶固有频率为优化目标。其中,影响各优化目标的设计变量P(1、5、6、7)在规定的取值空间内变化,构建的优化模型通过多目标遗传算法寻优。

3.5 构建稀疏网格模型

近年来,以Smolyak准则为基础的稀疏网格法被广泛地应用到插值、数据压缩、数值积分、微分方程的求解以及随机不确定性的传递等领域中[11]。它能够在一定程度上解决维数灾难问题,即传统数值积分计算量随变量维数呈指数级增长问题,因此其在高维积分问题上有着很好的适用性[12]。

使用稀疏网格方法求解一维模型问题的公式可以构建为

(10)

在求解高维度问题时,采用Smlolyak算法和张量积公式,模型的求解公式可以变换为

(11)

式中:d为所求解模型的维数;i1,i2,…,id为所求解模型各维度的精度等级;mi1,mi2,…,mid为求解模型各维度样本点的数目。

稀疏网格理论在其分层基函数的拟合精度方面也具有先验性,通过其分层近似模型,得到的拟合精度为

(12)

利用稀疏网格初始采样,在设计域空间自动抽取10个初始样本点进行计算,极大程度上减少了初始试验设计点的数量。维度自适应算法自动细化取点构建响应区域,快速达到指定响应精度,减少了构建响应面的时间。图12为稀疏网格模型预测值与实际值分布图。模型预测精度如表6所示。

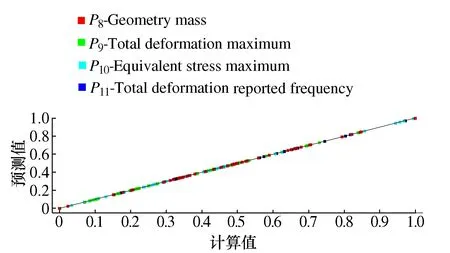
图12 预测值与实际值分布

表6 壳体多目标预测平均绝对百分比误差(MAPE) %

样本点和细化点拟合时越接近等值线,模型的预测精度越高[13]。由图12和表6可知:壳体的质量、最大变形、最大等效应力以及1阶固有频率的细化点均在等值线上;平均绝对百分比误差值很小,证明预测值与真实值差距较小,模型预测精度较高。该响应面具有可靠性并可以用来完成相关后续结构分析和优化任务。

计算求解后可以得到设计变量对优化目标影响的响应曲面,对各设计变量进行组合,能够获得不同的设计变量和优化目标之间的拟合图。图13所示分别为设计变量P5和P7对质量的响应图,底板厚度和加强筋的长度越大,则质量也越大;设计变量P1和P7对最大变形的响应图,两侧壁厚和加强筋长度越小,则最大变形越越大;设计变量P5和P6对最大应力的响应图,底板厚度和加强筋宽度越小,则最大等效应力越大;设计变量P1和P7对1阶固有频率的响应图,两侧壁厚和加强筋长度越大,则1阶固有频率越大。由此可以得知各设计变量与优化目标的影响关系图。

图13 参数响应图

3.6 MOGA遗传算法寻优

多目标优化问题可表示为

(13)

式中:x为决策空间，x=[x1,x2,…,xn]T∈RN,xn为决策变量;y为目标空间，y=[y1,y2,…yq]T∈Rq,yq为目标函数;gi(x)为可行解区域[14]，由m个不等式约束函数组成。采用多目标遗传算法来寻优时,最会得到一个均衡了各个目标函数的最优Pareto解集。

多目标优化技术是在响应面设计提供的优化样本集中,寻找“最好”的可行解。本文选用MOGA算法进行优化计算,MOGA 算法以生物自然竞争为优化原型,以目标函数为适应度控制个体淘汰或生存,简单易用,稳定性好,是一种具有全局优化性能并适合于并行处理的优化算法[15]。

为最大程度提升材料利用率,以质量最小值、最大变形、最大等效应力,1阶固有频率最大值为优化目标进行Pareto的搜索,搜索时将质量的客观重要性设置为Higher;最大变形、最大等效应力、1阶固有频率客观重要性设置为Default。MOGA遗传算法相关参数设置如表7所示。

表7 MOGA遗传算法参数设置表

4 结果分析及验证

基于MOGA算法搜索得到的3个优化备选方案如表8所示,以减轻质量为首选优化目标,选取方案1为最优方案。将最优方案的设计尺寸代入模型重新求解,得到优化后的应力云图及变形云图如图14和图15所示。最优解与初始解对比如表9所示。

表8 备选方案

图14 优化后变形云图

图15 优化后应力云图

表9 最优解与初始解对比

将优化前后的参数对比可知,减速箱壳体的质量由261.56 kg下降至214.27 kg,降低了18.1%;最大变形量由0.005 6 mm上升至0.010 6 mm;最大应力值由1.9 MPa上升至3.72 MPa,虽然最大变形值和最大等效应力值都有所增加,但它们依然满足强度与刚度要求。此方法有效提升了材料的利用率,实现了轻量化的目标。

使用优化后尺寸对壳体结构进行模态分析验证,壳体优化的固有频率及振型如表10所示。

表10 优化后壳体前6阶固有频率及振型

由表10可知,壳体优化后前6阶模态频率为322.08～897.01 Hz,模态频率虽有所减小但低阶模态频率依然避开了内部激励频率4.2～263 Hz,故壳体不会产生共振。

研究优化后静力分析和模态分析数据可知,该变速箱优化后的结构性能可以满足使用要求,实现了壳体减重的目的,达成了降本增益的目标,也证明了利用稀疏网格模型对变速箱壳体的轻量化设计是十分合理的。

5 结论

1)以碟簧为背景,对比分析传统近似模型与稀疏网格近似模型的预测精度,得出稀疏网格模型在预测精度方面更具优势。

2)对变速箱壳体进行静动态特性分析,结果表明壳体满足强度与刚度要求且不会产生共振,需对壳体进行轻量化设计,提高经济效益。

3)利用稀疏网格近似模型与MOGA遗传算法联合进行轻量化设计,使变速箱壳体重量减轻了18.1%,取得了较好的优化效果。为变速箱壳体轻量化提供了一种新途径,也可为其它机械结构优化提供参考。