铁路脱轨预警的尖点突变理论

张文静,张卜,许莎,刘学文

(上海工程技术大学 机械与汽车工程学院,上海 201620)

随着铁路技术的不断发展,列车的运行速度逐渐提高,重载列车也在不断增加,但是列车脱轨事故也明显增多,这对列车的运行安全性提出了考验。长期以来,列车的脱轨问题一直都是铁路运输系统研究中的重大课题。因此,结合现有的脱轨分析理论,寻求更准确的方法来预测列车安全运行状态是至关重要的。

车辆的脱轨问题一直以来都是世界各国专家学者们研究的主要课题。王健等[1]对准静态下的轮对脱轨模型进行受力分析,提出了基于轮轴脱轨系数和轮重减载率的轮对稳态脱轨评价方法。张茉颜和肖宏[2]建立了车-轨动力学模型,以脱轨系数和轮重减载率作为评判标准,分析车轮多边形对列车在小半径曲线段的运行安全性的影响。李万磊等[3]利用(短时)傅里叶变换方法对磁悬浮列车快变信号进行时域与频域的分析,实时监测和保证列车运行的安全性。Chung等[4]采用Monte Carlo模拟方法,分析了轨道的曲率半径、轮缘角及水平地震时加速度的变化对列车脱轨风险的影响,建立了基于Nadal公式的列车脱轨风险评估框架。Yu等[5]将轨道不平顺作为输入建立了基于BP神经网络和NARX神经网络的脱轨系数预测模型。

上述这些文章中所采用的列车脱轨评判准则多为Nadal脱轨系数法和轮重减载率判别法,然而这两种方法具有很大的保守性[6],在很多情况下都已不能充分的判别列车是否脱轨,因此需要考虑采用新的评价方法来研究列车的运行安全性问题。

由动力学理论来看,脱轨是列车丧失横向运动稳定性的结果。因此,曾庆元院士及其团队[7-8]根据弹性系统动力学总势能不变值原理及形成系统矩阵的“对号入座”法则,提出了列车脱轨能量随机分析理论,分析了列车脱轨过程中系统总能量的变化。Zhou等[9]利用能量增量准则说明了列车在桥上脱轨的机理,分析了列车脱轨的临界速度。

随着对列车脱轨现象的研究不断增多,评判脱轨的方法也越来越丰富。翟婉明院士[10]提出了利用车轮抬升量评判车辆脱轨的方法。孙善超[11]、雷虎军[12]等基于车轮抬升量分析车辆安全运行状态。Sun等[13]研究发现只有当车轮抬升量高于轮缘高度时,车辆才会发生脱轨。李俊成[14]分析了老牛湾站列车脱轨原因是在车钩力和道岔冲击作用下,轮对产生很大的横向轮轨力;轮轨间摩擦因数变大,车轮抬升量增加,最终导致车轮产生了爬轨行为。Zhu等[15]研究了列车碰撞脱轨机理,列车碰撞速度的增加会导致横摆偏转角急剧增大,从而导致轮轨横向力迅速增大,由此增加了车辆脱轨的风险。

此外,突变理论的提出也为列车脱轨机理的研究提供了一个新的思想。Wang等[16]采用尖点突变模型构建了铁路系统风险分析框架,描述了车-轨系统安全动态变化过程的规律。王阳鹏等[17]用于尖点突变理论研究了地铁列车自动监控系统(ATS)在运行时其安全状态的动态变化过程。李竹文和戴焕之[18]考虑脱轨系数和冲角对列车脱轨的影响,建立了尖点突变模型,通过分叉集模型给出了列车脱轨的危险区域,并建立车辆动力学仿真模型,验证该方法的有效性。刘文辉[19]则在脱轨系数和冲角的基础上,增加了脱轨系数超限时间这一参数,建立了车辆脱轨的燕尾突变模型,通过该模型的分叉集给出了车辆脱轨的临界区和脱轨区。但是已有的突变理论在列车脱轨上的研究都是考虑脱轨系数和冲角等参数的影响,很少涉及车辆-轨道系统中其他的影响参数。

实际上,列车脱轨是多种因素综合作用产生的结果,其过程非常复杂,很难用固定的表达式进行描述。列车由稳定运行到完全脱轨这一变化可以看作是一种突变行为,因此,完全可以利用突变理论研究列车的脱轨机理,解释列车脱轨行为发生的条件。本文基于尖点突变理论,考虑轮轨横向力和车轮抬升量对列车在曲线处脱轨的影响,建立了列车脱轨事故的尖点突变模型,对列车运行状态的突变过程进行分析,阐述脱轨机理,并根据分叉集得到列车脱轨的边界条件。通过SIMPACK建立车-轨仿真模型,验证突变理论在脱轨领域应用的可行性和正确性。

1 突变理论概述

在20世纪70年代,法国数学家Thom[20]提出了突变理论,主要用于研究动态系统在连续发展过程中出现突然变化的现象,解释突然变化与连续变化因素之间的关系。突变理论主要以建立复杂的突变数学模型来分析系统状态的突变现象。突变理论自提出以来已广泛应用于数学、力学、物理、生物学、社会科学等领域,都取得了丰富的研究成果。

事物的突变是一个非常复杂的过程,涉及的影响因素比较多,因此计算和求解的过程比较麻烦。因此,为了提高计算效率,Thom又提出了分类定理,将突变模型大致进行了分类。目前最常用的是7种初等突变模型,即折叠突变、尖点突变、燕尾突变、蝴蝶突变、椭圆脐点突变、双曲脐点突变和抛物脐点突变。不同的突变模型,所需要的状态变量和控制变量的个数不一样。

2 列车脱轨突变模型的建立

列车在实际曲线道路上行驶时,车-轨系统处于一种动态平衡状态,当列车遇到恶劣的外界环境干扰或很差的路况条件开始脱轨直至完全脱轨后,其系统状态发生了一个突变,这一变化是受很多因素影响的,因而完全可以用突变理论来描述列车的脱轨机理。根据突变理论的概念可知,列车脱轨事故的发生可以描述为动态系统内部控制变量的连续变化最终使得系统的状态发生了突变,最终导致列车脱离轨道。本文主要考虑了车轮抬升量和轮轨横向力对于列车运行状态的影响,采用尖点突变模型对列车脱轨事故进行分析描述,并提出了新的列车脱轨预警方法来预测列车在曲线处运行的安全性。

2.1 根据车轮抬升量判定脱轨的原理

车轮抬升量是指车轮踏面名义接触点与钢轨顶面最高点之间的垂向距离,是车轮爬升z1与跳动量z2(车轮与钢轨分离时)之和,即Zup=Z1+Z2,如图1所示。

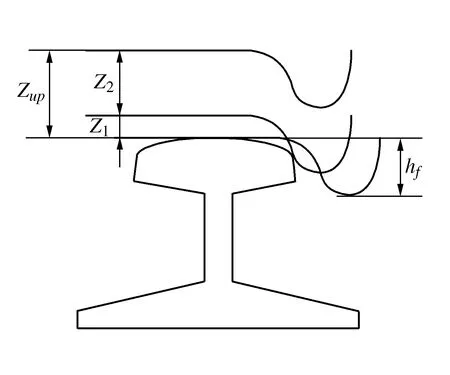
图1 车轮抬升量

当车轮抬升量小于车轮轮缘高度hf时,理论上可判定此时车辆未脱轨。当车轮抬升量等于轮缘高度,此时轮缘底部已跳到钢轨顶面最高点处,只要有微小的横向扰动车辆即刻发生脱轨,这种状态属于脱轨临界状态。而当zup>hf时,则判定车辆已脱轨。因此采用车轮抬升量评判车轮未脱轨的安全准则是:

(1)

2.2 根据轮轨横向力判定脱轨的原理

根据《铁路车辆动力学性能评定和试验鉴定规范》(GB5599-85)[21],对于木轨枕线路,单侧车轮轮轨横向力的限值为:

(2)

式中Pst为车辆的静荷载,kN。

对于混凝土轨枕线路,轮轨横向力的限值为

Q≤0.4Pw

(3)

即

Q≤0.4(Pst1+Pst2)

式中:Pw为静轴重,kN;Pst1、Pst2分别为左、右侧车轮静载荷,kN。

2.3 建立列车在曲线处脱轨的尖点突变模型

车辆在曲线处的运行过程中,由于轮轨接触状态及外界环境的影响,其状态是不稳定。现主要考虑车轮抬升量和轮轨横向力对于车辆运行状态的影响,建立尖点突变模型的势函数方程

V=V(x,u,v)

(4)

式中：V为列车-轨道系统安全运行的总势能;x为状态变量,表示列车的运行状态;u和v作为控制变量,则分别为车轮抬升量和轮轨横向力。

由《突变理论及其应用》[22]可知,尖点突变模型的势函数表达式为

V(x)=x4+ux2+vx

(5)

对势函数式(5)求一次导数可以得到突变流形图,其平衡曲面M的方程为

V′(x)=4x3+2ux+v=0

(6)

对平衡曲面M(5)求一次导数可以得到奇点集S,其方程表达式为

V″(x)=12x2+2u=0

(7)

联立式(6)与式(7)，消去x,得

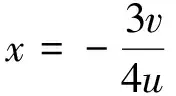
(8)

将式(8)代入式(7)化简得分叉集的方程为

8u3+27v2=0

(9)

式(9)的分解形式为:

u=-3x2

(10)

由此可画出列车在曲线处脱轨时的尖点突变模型图如图2所示。

图2 列车在曲线处脱轨的尖点突变模型图

图2中的曲面表示列车在曲线上运行过程中系统的平衡曲面,分为上叶、中叶和下叶;其中,上下两叶是处于稳定状态的,而中叶上的褶皱部分表示系统发生了突跳,是不稳定的。控制空间上的曲线是平衡曲面中叶的褶皱部分在底平面上的投影,称为分叉集,表示列车脱轨事故发生的条件。由平衡曲面可以看出,当系统的运行状态从上叶的稳定在轨运行跃迁至下叶的脱轨后的稳定状态,说明列车的运行状态发生了突变,即列车脱离轨道,发生事故,这一过程是在列车运行中最危险的,也是需要避免的。

2.4 突变分析

列车在曲线处运行过程中,列车运行状态在车轮抬升量和轮轨横向力的作用下发生突变的现象可以通过尖点突变模型进行理论性解释。列车的运行状态由空间的点来表示,在车辆平稳运行时,空间的相点必在曲面的上叶或下叶;当相点逐渐移动到上下叶边缘时,由于中叶的非稳定状态无法存在,所以相点将直接跨越中叶突跳到另一叶上的平衡位置,此时列车的运行状态就会发生突变。

本文选择C64k型敞车,其技术参数见表1。

表1 C64k型敞车的技术

由《铁路车辆动力学性能评定和试验鉴定规范》(GB5599-85)[20]可知,磨耗型车轮踏面的车轮抬升量极限值为27 mm,轮轨横向力极限值为Q=0.4×(21/4)×9.8=20.58 kN。因此尖点突变模型中分叉集的横纵坐标取值分别为20.58 kN和27 mm,如图3所示。

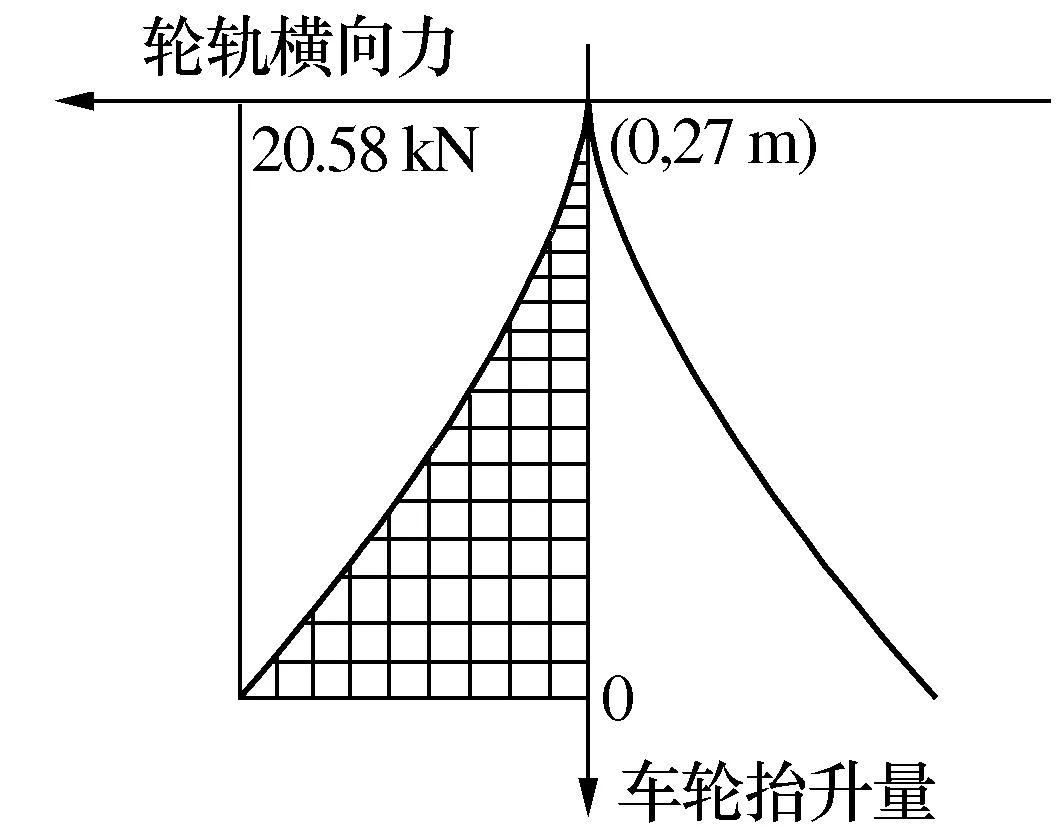
图3 列车在曲线处脱轨的尖点突变分叉集

尖点突变模型平衡曲面上的褶皱部分在控制平面上的投影称为分叉集,如图3所示。分叉集的左半部分表示列车由稳定运行状态向脱轨状态变化,此时空间中的点在控制变量的作用下从上叶跳至下叶导致系统的状态发生了改变,这种突变是有害的。分叉集的右半部分表示列车由突跳状态向稳定在轨运行状态变化,此时,列车在控制变量的作用下跳上轨面运行一段时间后又掉回轨道,重新进入平稳运行状态,在此期间,轮对虽发生了突跳但没有脱离轨道,因此该突变是有益的。结合图2和图3可知,分叉集左侧曲线以上区域为系统发生突变导致列车脱轨的危险区域。由图3可知,随着车轮抬升量的不断增加,列车脱轨的危险区域也在不断扩大,因此列车脱轨的可能性增加。当车轮抬升量和轮轨横向力的数值落在脱轨危险区域的下方,则可判定列车未脱轨。若控制变量的取值落在分叉集左侧曲线以上区域内,则列车就会脱离轨道,发生严重的脱轨事故。因此,减小车轮抬升量可以有效的降低脱轨的可能性,从而可以防止列车脱轨事故的发生。

3 突变模型的仿真试验验证

本文基于初等突变理论建立了尖点突变模型,并根据分叉集给出了列车在曲线处脱轨的危险区域。现利用SIMPACK软件建立车辆系统动力学模型,通过仿真分析验证突变模型的正确性与实用性,具体的仿真过程如下。

选择C64k型列车,根据车辆的基本参数,建立车辆系统动力学仿真模型,如图4所示。

图4 车辆系统动力学模型

对该模型施加美国六级轨道方向不平顺激励谱,设置5种不同线路条件的工况,研究车轮抬升量和轮轨横向力在120 km/h的速度下的变化情况,如表2所示。

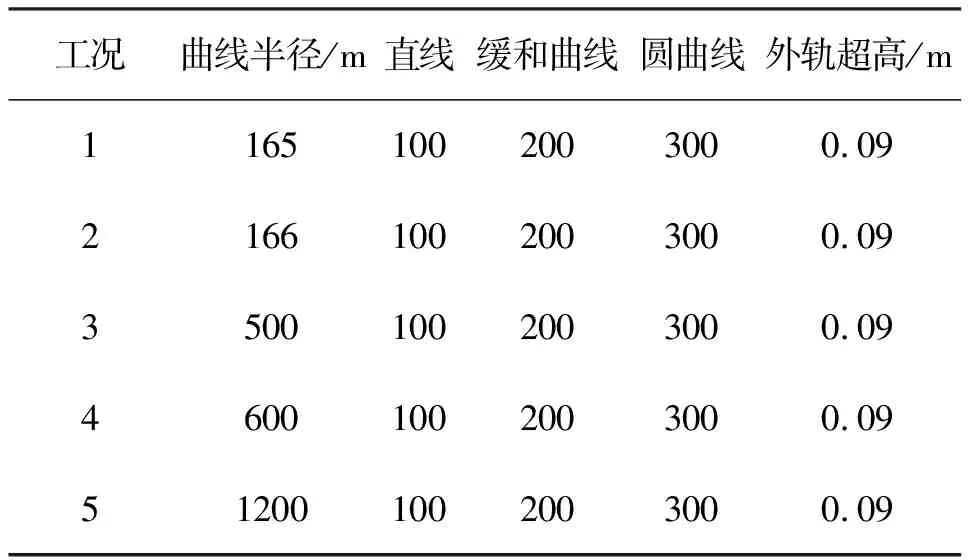
表2 线路条件的设置

设置列车的运行速度为120 km/h,外轨超高量为0.09 m。通过改变线路的曲线半径,得到了车轮抬升量和轮轨横向力随时间变化的图形,如图5所示。由图5可知,曲线半径越大,轮轨横向力和车轮抬升量的数值就越小,列车的运行状态就越稳定。当曲线半径小于166 m时,车轮抬升量成直线状态急剧增加,超过了允许的极限值27 mm,此时轮轨横向力也大于20.58 kN,对应于尖点突变模型分叉集的左侧曲线以上区域,因此,可以判定列车脱离轨道,发生事故。

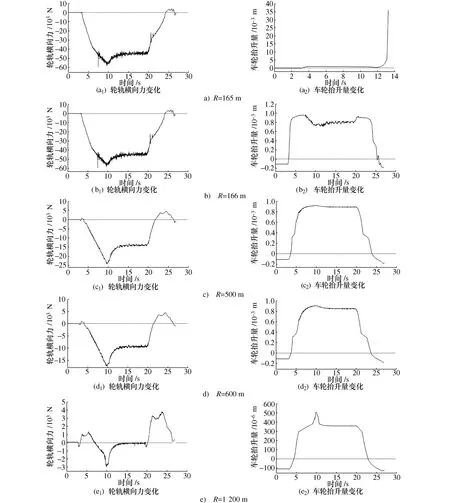
图5 不同曲线半径工况下,车轮抬升量和轮轨横向力随时间变化的情况

当曲线半径处于166～600 m之间时,车轮抬升量在0.9 mm附近上下浮动,而轮轨横向力超出了极限值,此时也是对应于分叉集左侧曲线以上区域,列车存在脱轨危险。当曲线半径大于600 m时,从图5可以看到车轮抬升量和轮轨横向力都是处于安全范围内的,因此列车的运行状态是稳定的,不会发生脱轨事故。

4 结论

基于初等突变理论,本文讨论了列车在曲线处由稳定在轨运行到完全脱轨后的状态突变过程。选择车轮抬升量和轮轨横向力作为控制变量,列车运行状态为状态变量,建立尖点突变模型，确定控制变量的极限值,由此得出尖点突变模型的分叉集,并对其突变特性进行突变分析,给出了列车可能发生脱轨的危险区域。应用SIMPACK仿真软件建立车辆系统动力学模型,通过改变线路的曲线半径大小,分析车轮抬升量和轮轨横向力随时间的变化情况。结果表明,当曲线半径小于166 m时,车轮抬升量和轮轨横向力都远大于极限值,列车发生脱轨;当曲线半径大于600 m时,列车运行状态比较平稳安全。