一类曲线上Cauchy积分在尖点处奇异性的探究

贾婕，刘华，边小丽

一类曲线上Cauchy积分在尖点处奇异性的探究

贾婕，刘华，边小丽

（天津职业技术师范大学 理学院，天津 300222）

带尖点曲线；Cauchy型积分；跳跃问题；典则函数

1　尖点处Cauchy型积分奇异性结论推广

1.1　３条封闭曲线相切相交

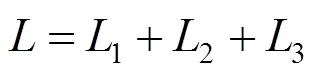
图1 含尖点３条曲线交叠图

与文献[10]中2条曲线时所得结论相比，3条曲线相切相交可以更直观地反映这类特殊曲线上尖点附近奇异性在不同区域的变化．

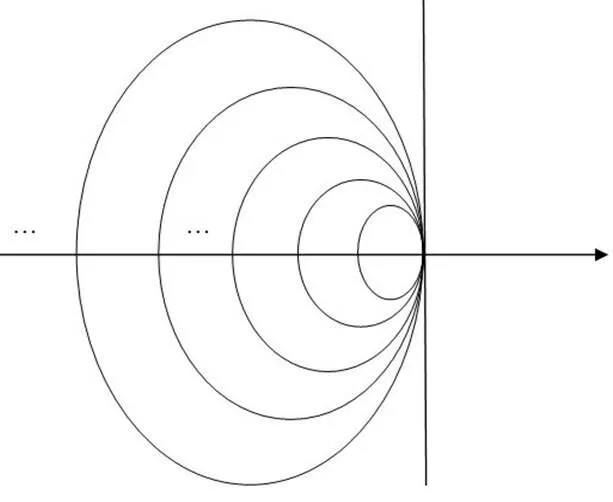
图2 含尖点条曲线交叠图

2　特殊含尖点曲线上Riemann边值问题求解

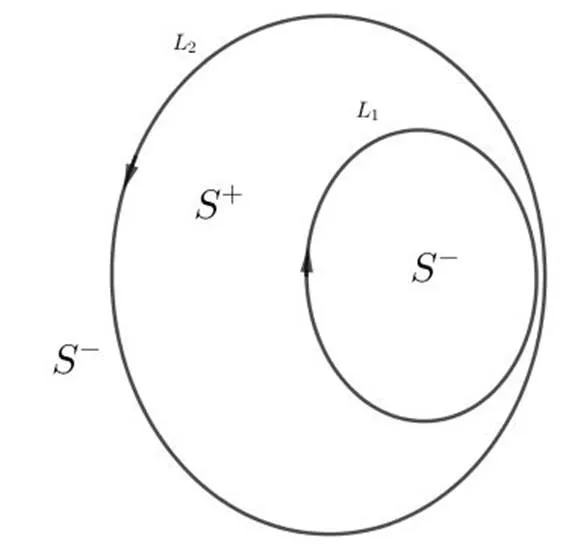
图3 二次跳跃问题曲线

2.1　一般曲线上Riemann边值问题求解

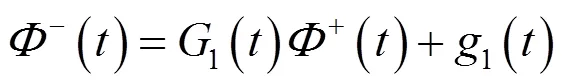
对于给定

二次齐次跳跃问题合并后的典则解为

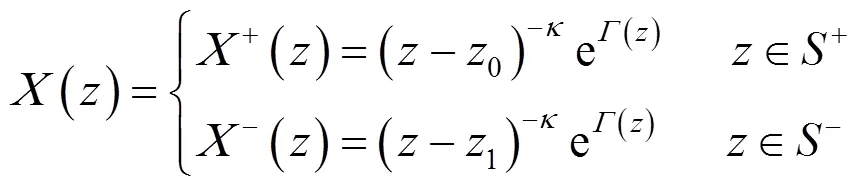
考虑非齐次问题

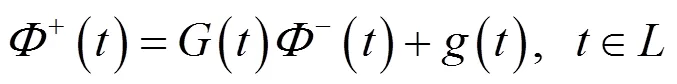
2.2　尖点处奇异性制约条件对解的影响

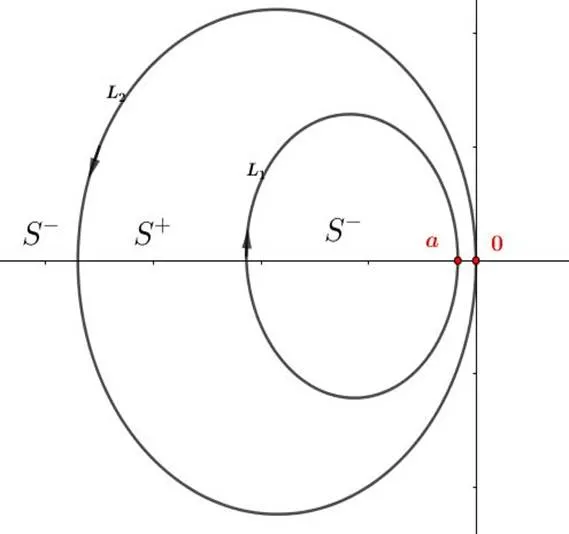
图4 平移曲线

图5 局部取极限

图3中跳跃问题的解函数（即不考虑尖点时的解）

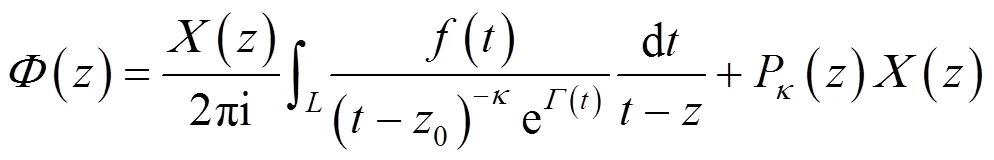
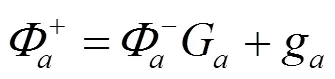
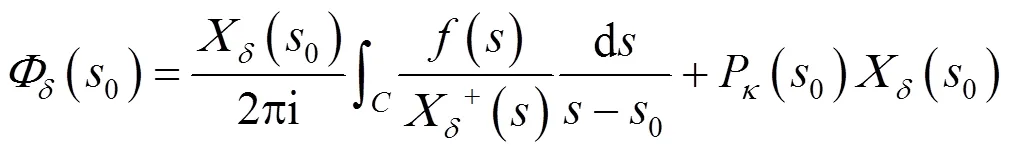
相应地，平移后含尖点曲线上解的表达式中的典则函数变为

结合文献[10]中由２条封闭曲线相切相交产生尖点的特殊曲线上表示Riemann边值问题解的Cauchy型积分奇异性的结论，本文平移曲线求极限的方向和过程类似于由区域①向尖点处取极限，区域①情况下尖点处的奇异性被抵消，此带尖点曲线上的Riemann边值问题也转化为一般的不受尖点奇异性影响的复合边值问题求解．

[1] 路见可．解析函数边值问题教程[M]．武汉：武汉大学出版社，2009

[2] 王莹，段萍，杜金元．正实轴上的Riemann边值问题[J]．中国科学：数学，2017，47（8）：887-918

[3] 路见可．不同材料拼接平面裂纹中的数学问题[J]．武汉大学学报：自然科学版，1982（2）：1-10

[4] 李星．一类周期裂纹问题的数值解[J]．宁夏大学学报：自然科学版，1998，19（1）：45-46

[5] 张军好，刘华．周期弹性平面裂纹探测的复变方法[J]．武汉大学学报：理学版，2009（4）：386-390

[6] Deift P．Orthogonal Polynomials and Random Matrices：a Riemann Hilbert approach[M]．New York：American Mathematical Society，2000

[7] Deift P，ItsA，KrasovskyI．Asymptotics of Toeplitz，Hankel，and Toeplitz+Hankel determinants with Fisher-Hartwig singularities[J]．Annals of Mathematics，2011，174：1243-1299

[8] Deift P，Zhou X．A steepest descent method for oscillatory Riemann-Hilbert problems[J]．Bulletin of the American Mathematical Society，1992，26（1）：119-123

[9] Fokas A S，Its A R，Kitaev A V．The isomonodromy approach to matrix models in 2D quantum gravity[J]．Communications in Mathematical Physics，1992，147：395-430

[10] 贾婕，刘华，边小丽．一类特殊曲线上Cauchy积分在尖点处奇异性分析[J]．天津职业技术师范大学学报，2020，30（1）：26-29

Exploration of the singularities of Cauchy integral at the sharp point on a kind of curves

JIA Jie，LIUHua，BIAN Xiaoli

（School of Science，Tianjin University of Technology and Education，Tianjin 300222，China）

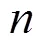
curve with sharp point；Cauchy type integral；jump problem；canonical function

O174.5

A

10.3969/j.issn.1007-9831.2020.06.003

1007-9831（2020）06-0010-06

2020-03-25

天津职业技术师范大学研究生创新基金项目（YC19-37）；国家自然科学基金项目（11802208）

贾婕（1995-），女，甘肃定西人，在读硕士研究生，从事解析函数边值问题研究．E-mail：JiaJie951121@163.com