ANALYTIC BOUNDARY VALUE PROBLEMS ON CLASSICAL DOMAINS∗
Hua LIU(刘华)
Department of Mathematics,Tianjin University of Technology and Education,Tianjin 300222,China
ANALYTIC BOUNDARY VALUE PROBLEMS ON CLASSICAL DOMAINS∗
Hua LIU(刘华)
Department of Mathematics,Tianjin University of Technology and Education,Tianjin 300222,China
E-mail:hualiu@tute.edu.cn;daliuhua@163.com
In this paper analytic boundary value problems for some classical domains in Cnare developed by using the harmonic analysis due to L.K.Hua.First it is discussed for the version of one variable in order to induce the relation between the analytic boundary value problem and the decomposition of function space L2on the boundary manifold.Then an easy example of several variables,the version of torus in C2,is stated.For the noncommutative classical group LI,the characteristic boundary of a kind of bounded symmetric domain in C4,the boundary behaviors of the Cauchy integral are obtained by using both the harmonic expansion and polar coordinate transformation.At last we obtain the conditions of solvability of Schwarz problem on LI,if so,the solution is given explicitly.
complex partial differential equation;analytic boundary value problem;singular integral;bounded symmetric domain 2010 MR Subject Classification 32A26;32A40
1 Introduction
It is well known that in Cnthere does not exist a complete analogue of the Riemann boundary value problem in C.Given a smooth hypersurface S in Cnand a H¨older continuous function g(t)on S,suppose that there exists a sectionally holomorphic function Φ(z)in CnS such that
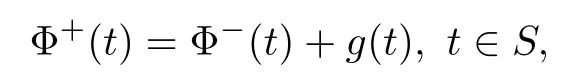
where Φ±(t)are the boundary values of Φ(z)at both sides of S respectively.Then Hartogs theorem says that Φ(z)must be a holomorphic function in a tube neighborhood of S,which means that g(t)must be a CR function on S[1].
However,the Riemann boundary value problem in C is such a successful tool for many subjects in mathematics,physics and engineer techniques that it will be sad to suspend these ideas and techniques in the higher dimension of complex spaces.So many people attempt to look for its new version in the case of several variables[1-5,7,8,10,13].Here we discuss this work by the method of the harmonic analysis on classical groups[6].
Let RI(2,2)denote the domain in C4for which
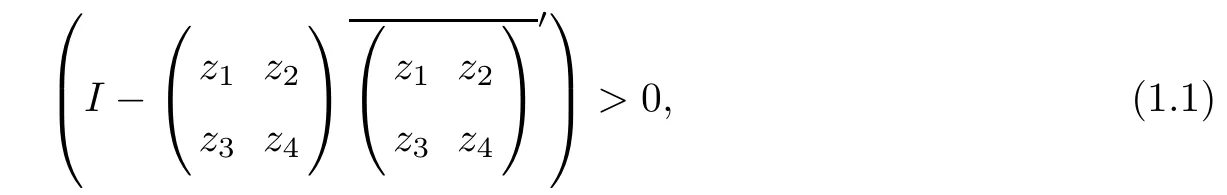
where>means that the left-hand side is a positively definite 2×2 matrix[6].Similarly letdenote the set of negatively definite 2×2 matrices and LIthe common characteristic(Shilov)boundary,or the vertex manifold,of both RIand R∗I.LIconsists of the 2×2 matrices U satisfying UU′=I,i.e.,the unitary matrix.Here we do not use its usual name U(2)since U is the variable in C4(sometimes written as 2×2 complex matrix,and we do not distinguish them)in this paper.
Now we state a special analytic boundary value problem,Schwarz problem,in the first Cartan domain RIwith the boundary of group LIin C4,which is the over-determined system
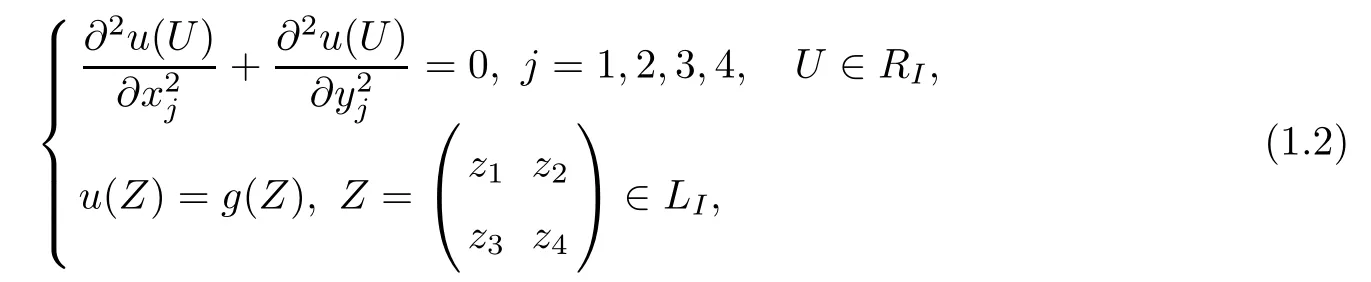
where xj+iyj=zj,j=1,2,3,4,and g(Z),u(U)are real functions.Moreover,the given function g(z)will be shown to belong to Lip1+∈(LI)(ǫ>0)in the proof of the rest of this paper,here f∈Lip1+∈(LI)if and only if f′∈H∈,H¨older space with exponent of ǫ.(1.2)can also be reformulated as follows
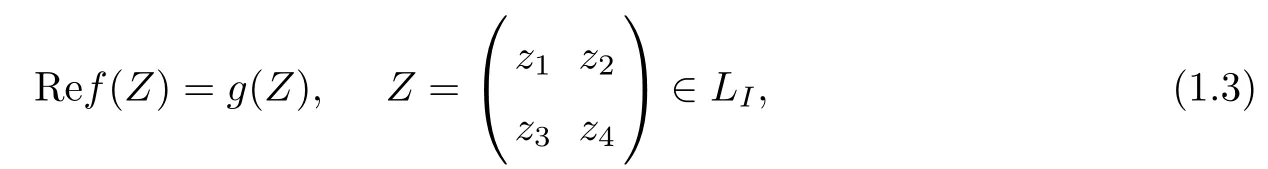
where f(U)is holomorphic in RIand continuous on RI∪LI.Of course,u(Z)is the real part of f(Z)in RI,and so a pluriharmonic function.
It is important to discuss these problems by the use of the orthogonal expansions of the jumped functions on the boundary manifold.We first retrospect with the clues for both cases of the unit circle∂D in C and the bicircle or torus∂0D2in C2.It appears that the relation between the harmonic expansion and Cauchy type integral plays an important role on the analytic boundary value problems on∂D,∂0D2and the classical group LI.
2 The Case of∂D
We first discuss the analytic jump boundary value problem on∂D.
For f(t)∈L2(∂D)there exists the Fourier expansion
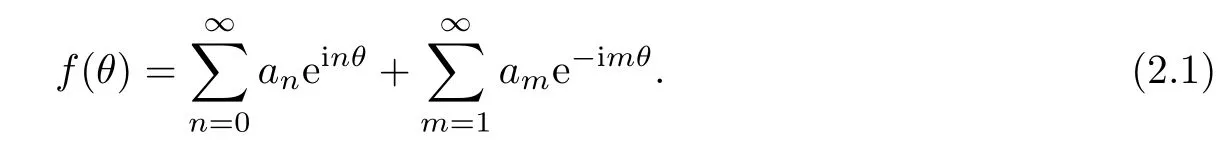
Let S∂Ddenote the singular integral operator with Cauchy kernel on∂D.Define the operators P±=12(I±S∂D)on L2(∂D),then[4]
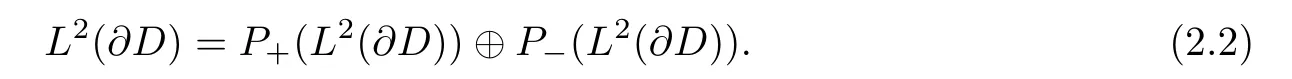
By[9],for f(t)∈L2(∂D)there exists a unique sectionally holomorphic function Φ(z)in C such that
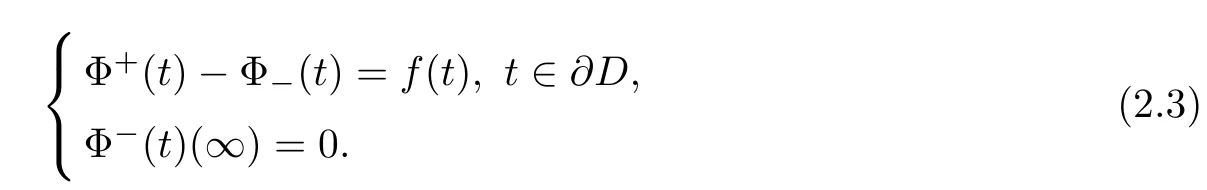
And
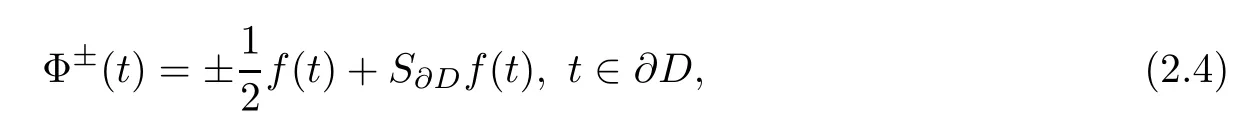
where φ±are the boundary values of the Cauchy integral
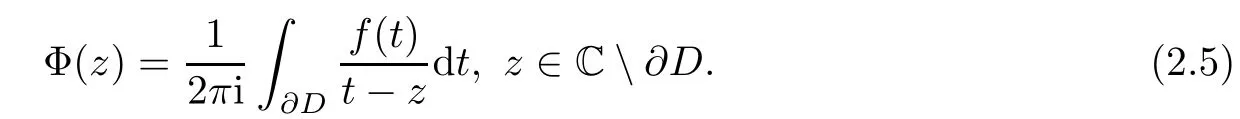
(2.4)gives the relation between the Riemann boundary value problem and singular integral,i.e.,the singular integral can be defined by the former
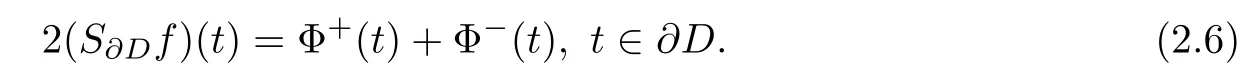
The Poison kernel of D
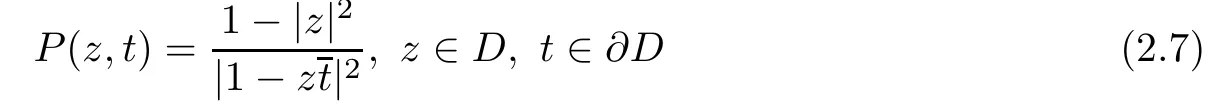
is the difference of the Cauchy kernels of the D+and D-in the sense that
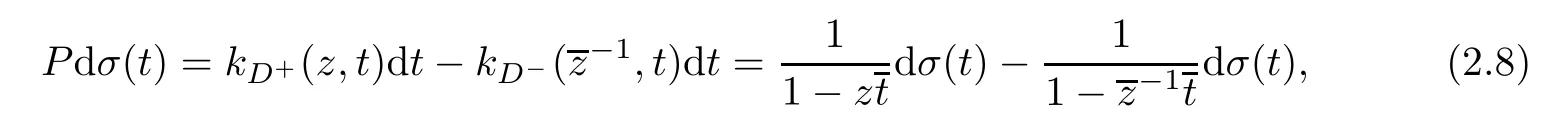
then
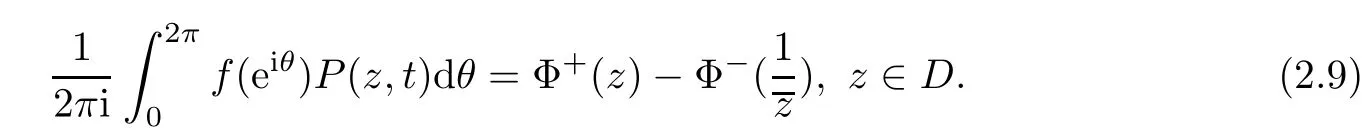
So when z approaches t0∈∂D non-tangentially,we have

which just is the Poison formula.
From(2.2)to(2.10),it is clear that the solution of the Riemann boundary value problem provides a complete decomposition of L2(∂D).
The other Riemann boundary value problem is formulated as

where a(t)∈Hµ(∂D)(µ>0)and f∈Ω(D+)∩Hµ(D+).
Define
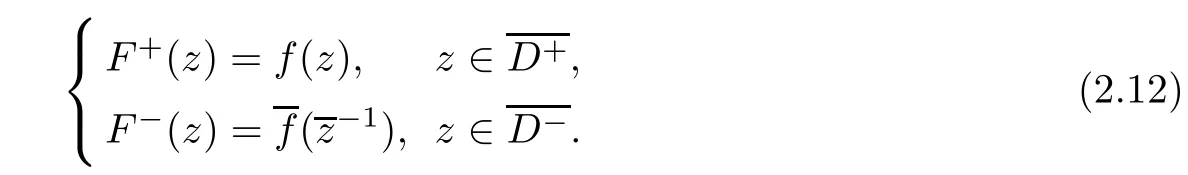
It may be easy to prove that(2.11)is solvable only if the Riemann boundary value problem
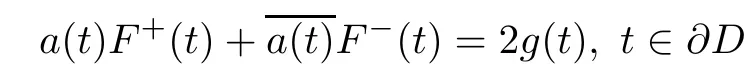
is solvable[9].Especially,when a(t)is constant function,say 1,(2.11)is always solvable and the solution represented by so called Schwarz formula
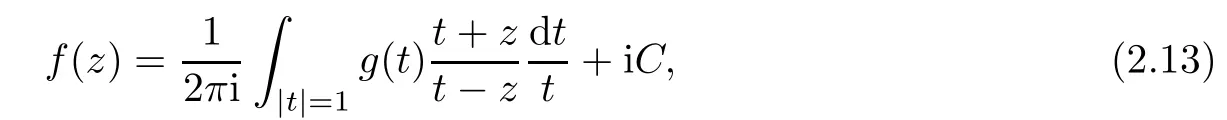
where C is a real constant.
3 Cauchy Integral on LI(2,2)
First we consider the analytic boundary value problem on∂0D2,the characteristic boundary of the bidisc.We define
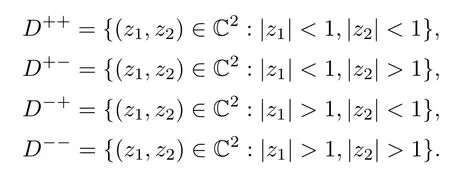
Then∂0D2is their common vertex and
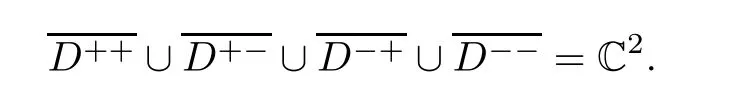
It is difficult to get the formula similar to(2.4)by the singular integral operator over L2(∂0D2)since it is complicated to deal with the latter[11].The Wiener algebra W(∂0D2)is the suitable choice at present.Let ϕ belong to W(∂0D2),then ϕ has the following expansion[10]
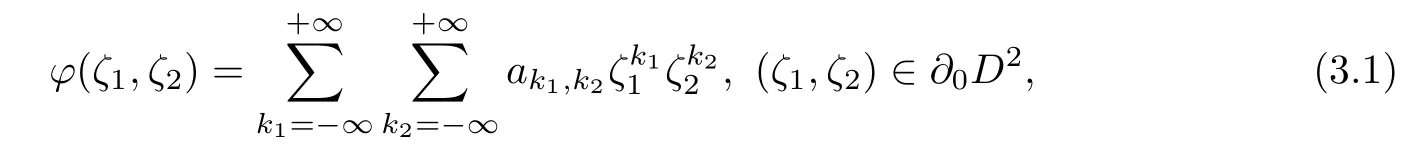
where

For ϕ∈L2(∂0D2),introduce the so-called integral of Cauchy type in C2by

So Φ(z1,z2)is analytic in C2∂D2and Φ(z1,∞)=Φ(∞,z2)=0. Define the four boundary values of Φ on∂0D2by
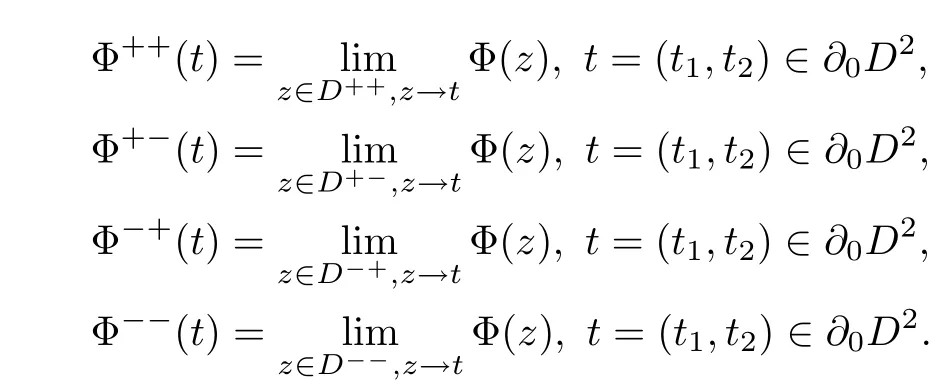
In[2]it is discussed in detail for these boundary values,one result of which is the following lemma.
Lemma 3.1 When(z1,z2)approaches(t1,t2)∈∂0D2,there exist the boundary values of Φ such that
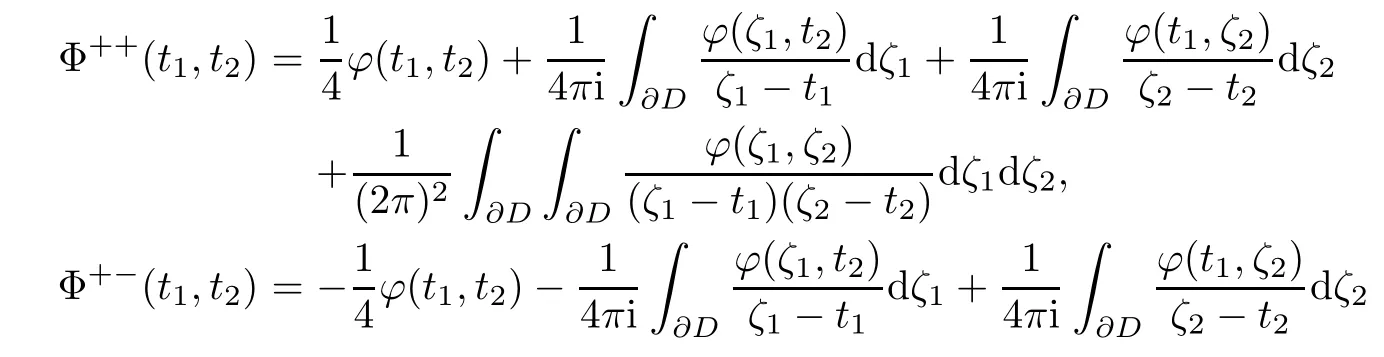
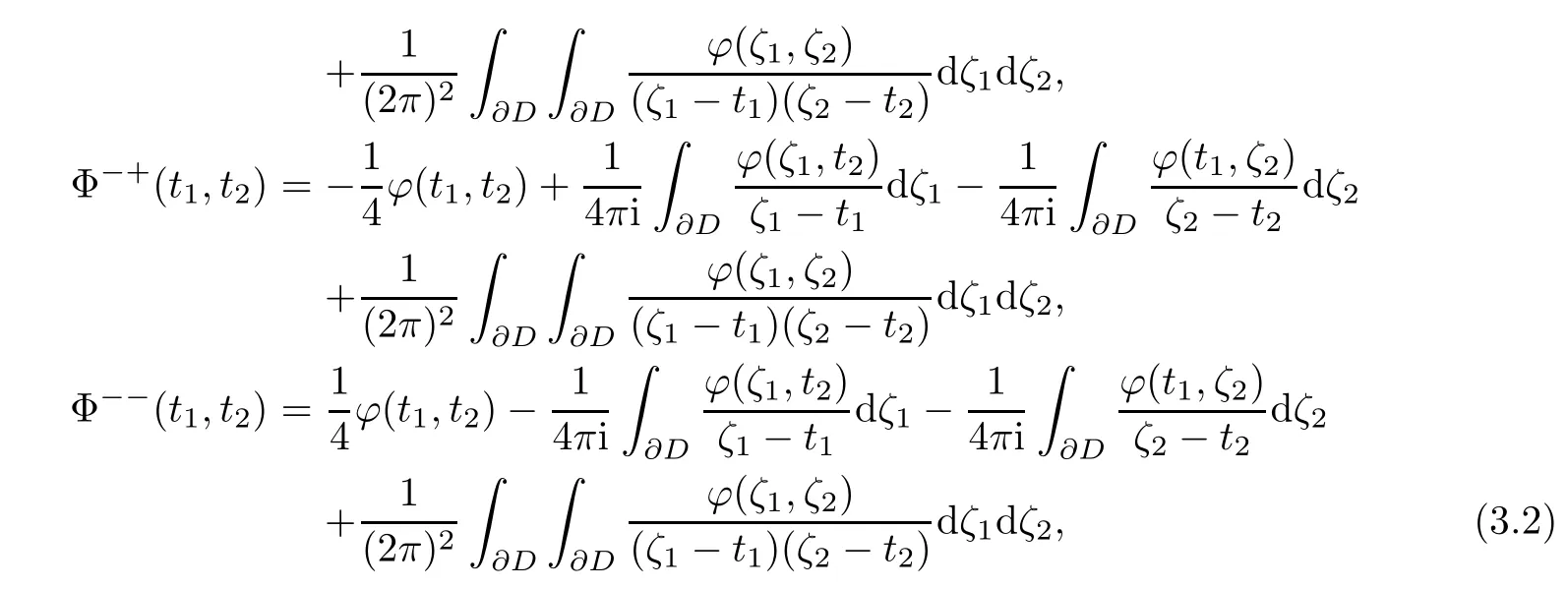
where the singular integral of two dimension
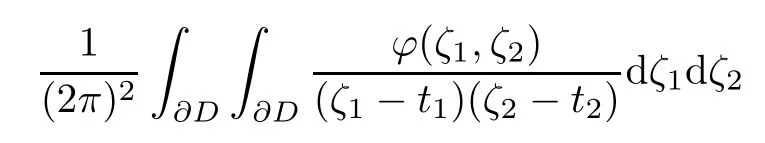
is defined step by step in the ways of single variable.
It was proved in[2]when f is H¨older continuous,but which is also valid for f∈L2(∂0D2)by Banach extension theorem.As(2.6)we can say the singular integral of ϕ(t)on∂0D2satisfies
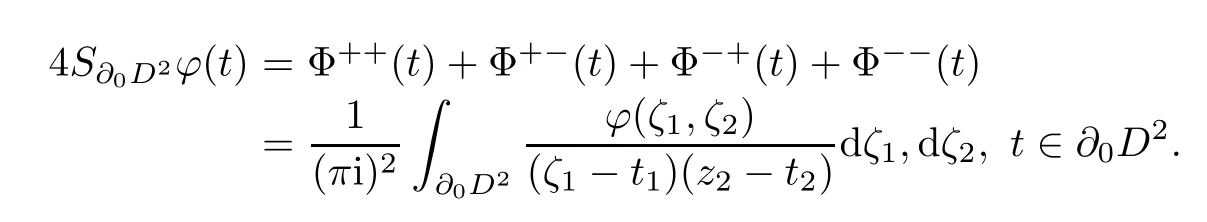
The above formula is nontrivial since there exist more than one definitions of a singular integral in several complex variables[11].
It is well known that∂0Dnis the unique commutative compact Lie group.It is much more difficult to deal with the noncommutative group LI(2,2),i.e.,the unitary group U(2)consisting of 2×2 unitary matrices.
By some similar ideas,we try to discuss the analytic boundary value problem on the submanifold LI(2,2)in C4.We have defined in section 1 that RIis the set of 2×2 complex matrices Z satisfying I-ZZ′>0,and R∗Isuch that I-ZZ′<0.Then both RIand R∗Iare domains in C4and LIis the characteristic boundary of RI.Denote R◦I=C4(RI∪R∗I).
Let˙U denote the volume element of LIand Vol(LI)the volume of LI.Suppose that F(Z)and G(W)are holomorphic functions on RIand R∗Iand Lip1+∈continuous on their closures respectively.Then[6]
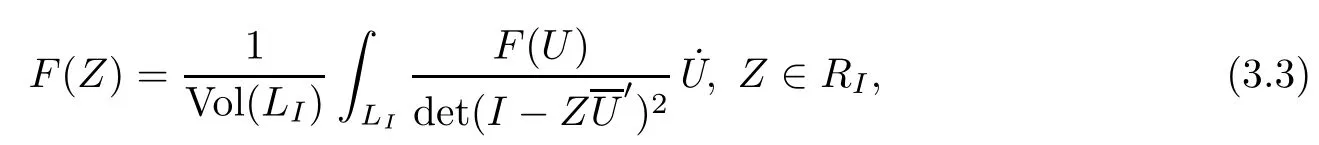
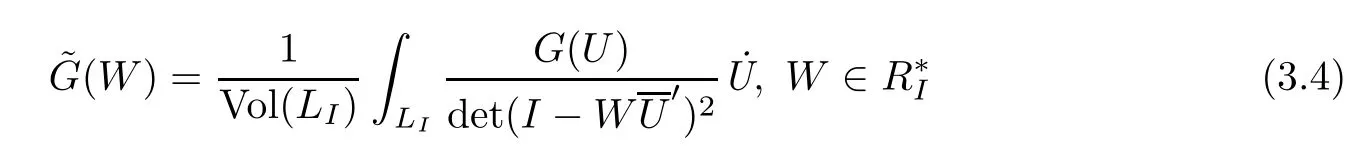
is a holomorphic function of W-1,it is still more difficult to say what relations are betweenand G(W).
By Weil theorem there exists a complete orthogonal baseconsisting of the elements of all unitary irreducible representation matrices of LIin the spaces spanned by thehomogeneous monomials
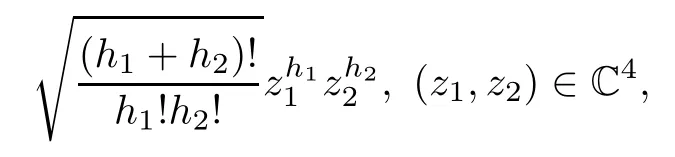
where h1<h2and 1≤i,j≤N(h)(the dimensions of the representing spaces).Suppose that ϕ(U)is a continuous function in LIand then
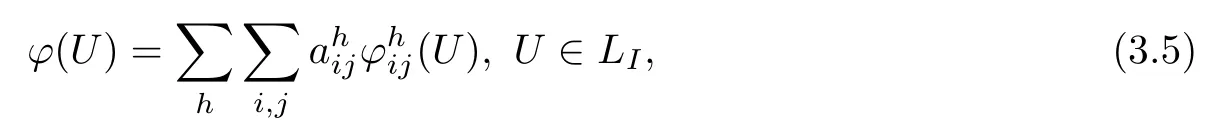
where the right-hand side is the Abelian summable[6].
Define the Cauchy integral of ϕ(Z)on LIby
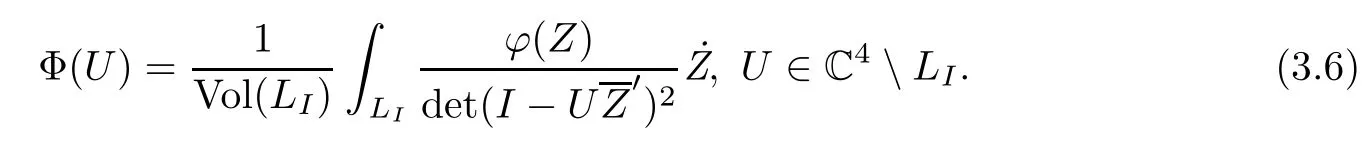
Now Φ(Z)is holomorphic on both RIand R∗I.But(3.3)does not work in R◦Isince there always exist U∈LIsuch that det(I-ZU′)=0 for any Z∈R◦I.We write

Then Φ±(Z)have the following expansions
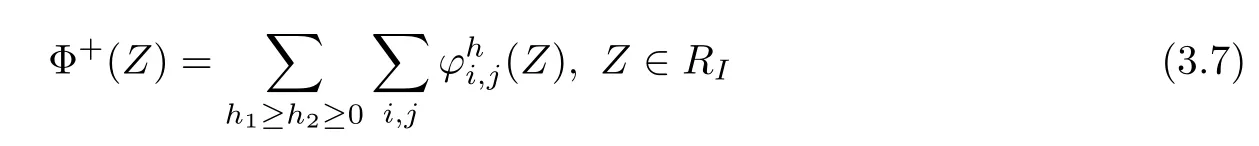
and
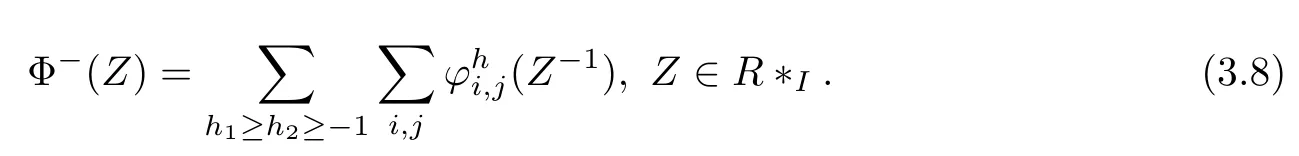
Comparing(2.1),(3.1)with(3.7)and(3.8),it is interesting thatvanish for h1<-1 or h2<-1 in(3.8)!
We need to study the boundary behavior of the Cauchy integral(3.6).Denote the boundary values by
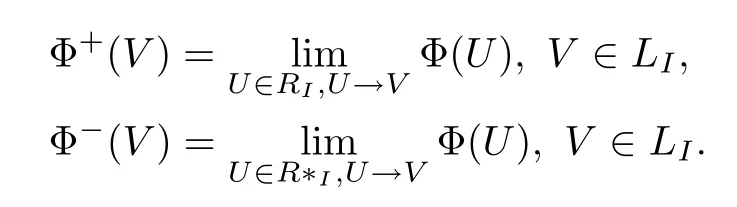
It is enough to deal with the boundary value of Φ at the unit matrix I since LIis a symmetric manifold.Using the symbol in[6],by the polar coordinates for LIwe have
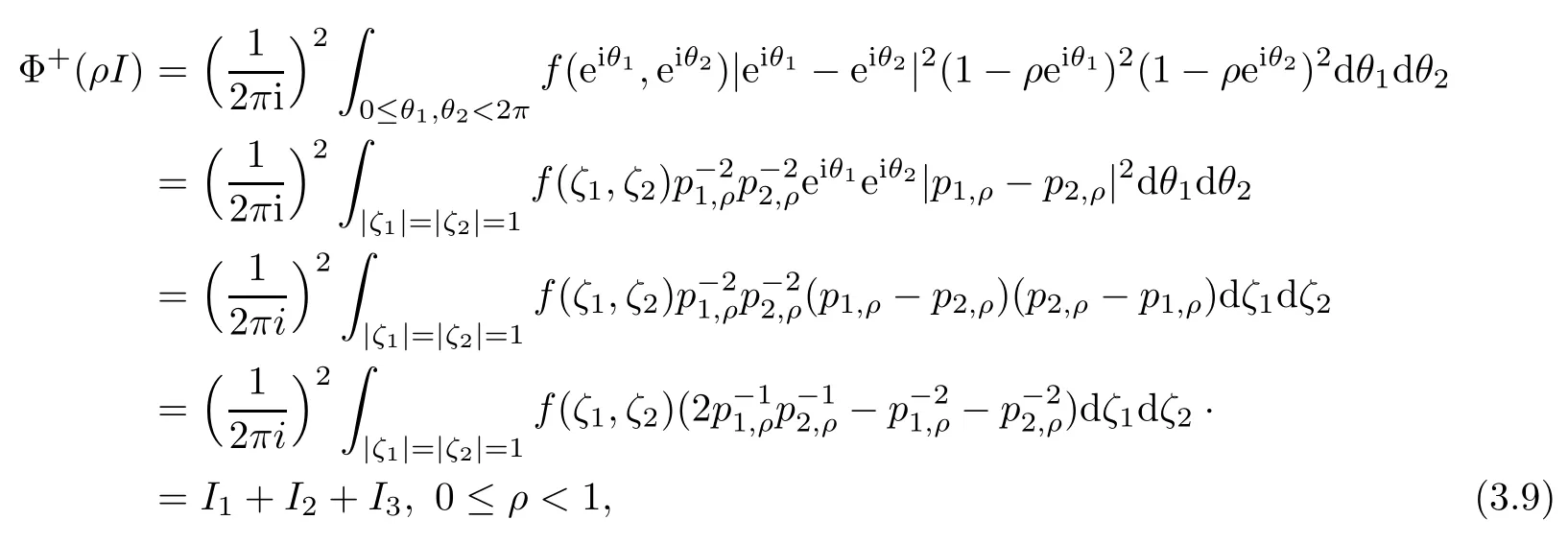
where pj,ρ=(ζj-ρ),j=1,2,and
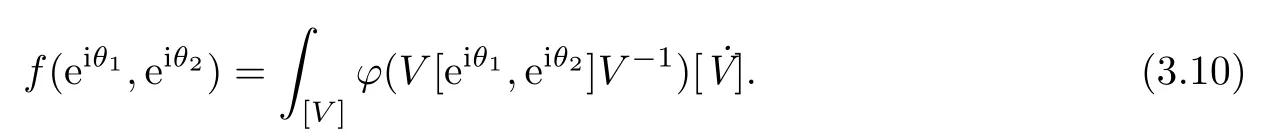
When ρ approaches 1,the above integral can be represented by the higher singulary integral,for which the derivatives of ϕ must be H¨older continuous,i.e.,ϕ must belong to Lip1+ε.By Lemma 3.1 we can work out the boundary value in detail as follows.
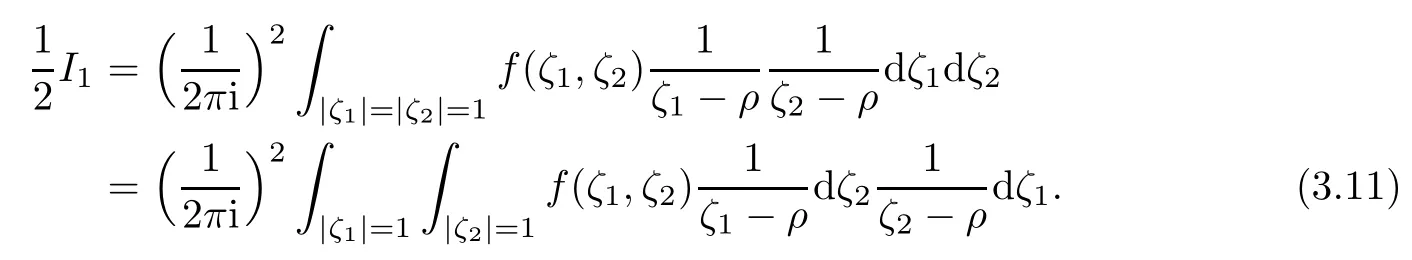
So
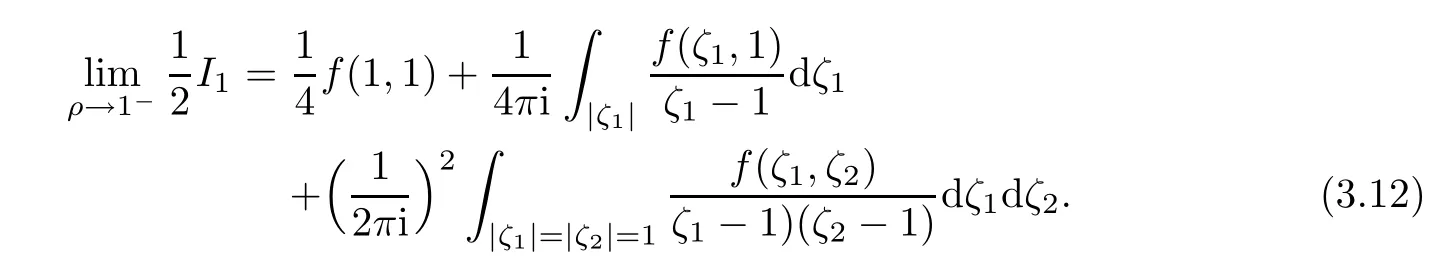
By partial integration we get
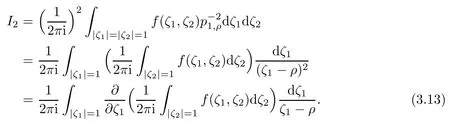
Again
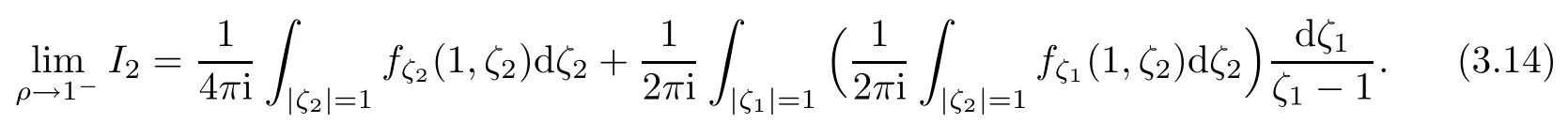
Similarly
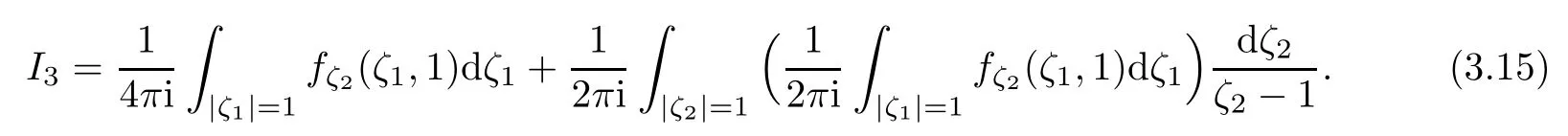
The integral in(3.12),(3.14)and(3.15)should all be considered to be singular integrals as(3.2).
Theorem 3.2 By(3.10)-(3.15),we have
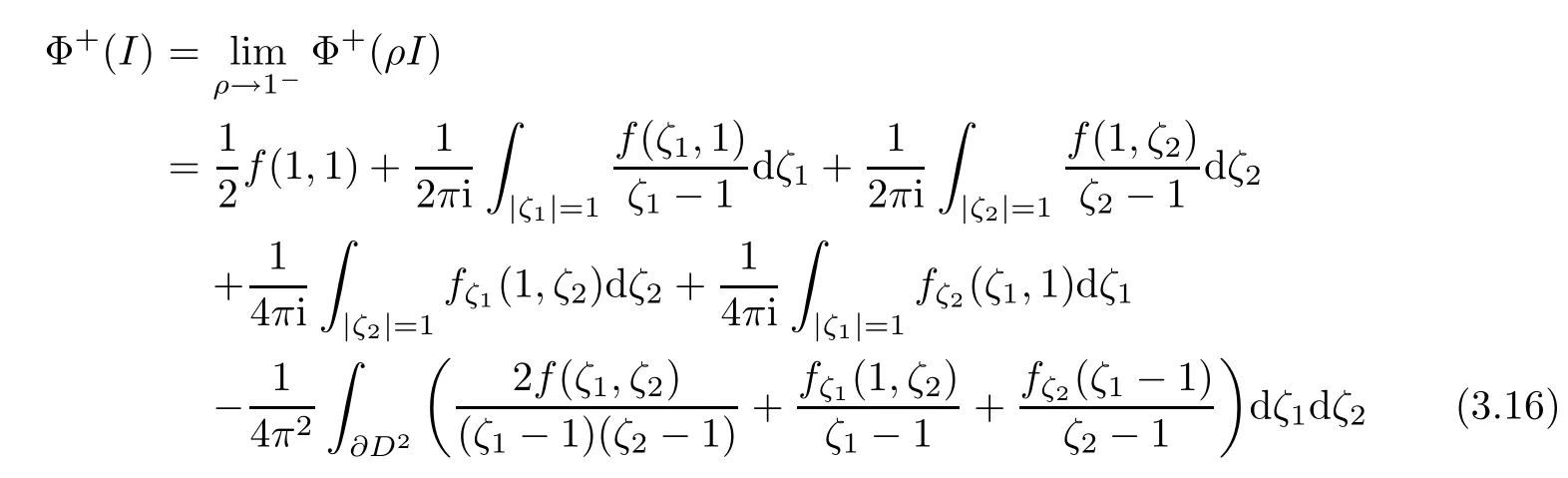
and
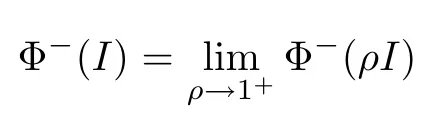
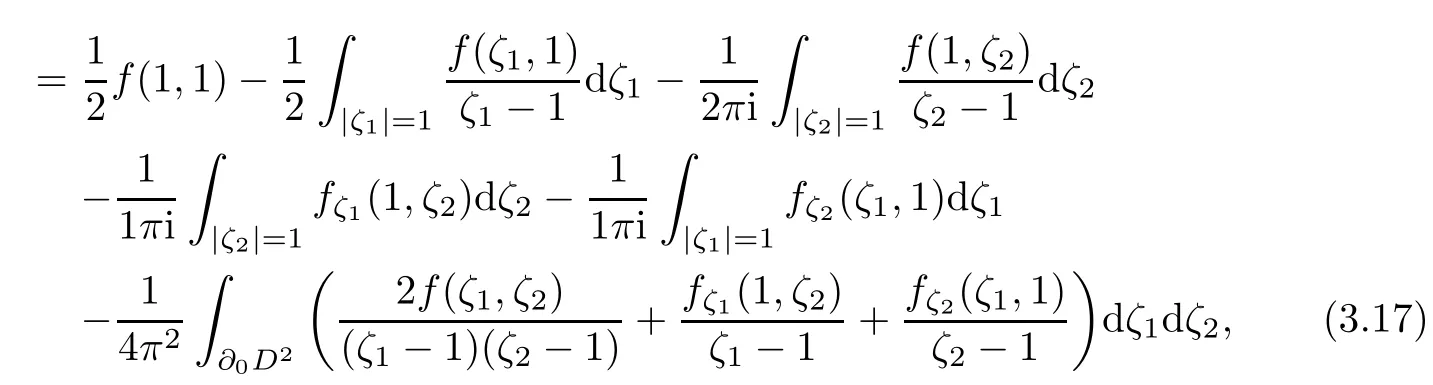
where I is the unit 2×2 matrix and f given in(3.10).
Although the above singular integrals are defined by repeatedly applying the one dimensional version,they are equivalent to the Caredelon-Zygmand integral[11].
4 Main Results
In this section we discuss the following problem.
Problem A Let the real function ϕ(U)∈Lip1+∈(LI).Does there exist a holomorphic function S(Z)in RI(2,2)such that

Let us begin with the following theorem.
Theorem 4.1 Let ϕ(U)∈Lip1+∈(LI),then there exists a unique solution to the following boundary problem
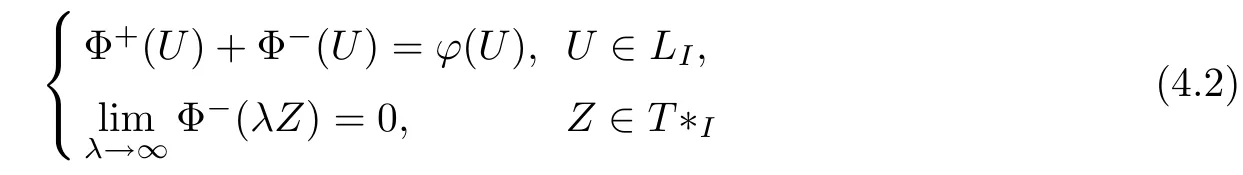
if and only if
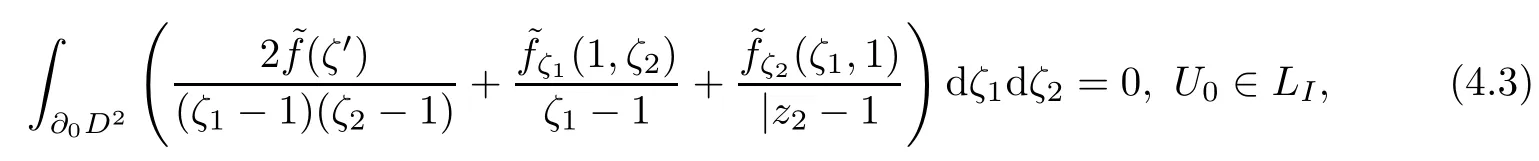
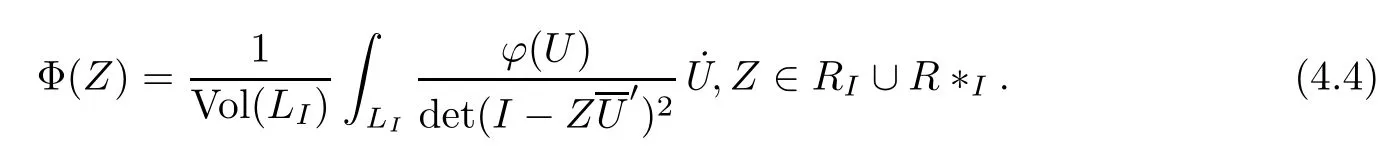
Proof By(3.16)and(3.17),it is easy to prove the existence and the necessity.We only need to show that there exists only one solution for ϕ=0.Otherwise,Let Φ be a solution of Problem A.For U0∈LI,the complex line Cλ={λU0,λ∈C}in C4intersects LIon a unit circle which divides Cλinto two complements belonging to RIand R∗I,respectively.By the Riemann boundary value problem in C,Φ vanishes in Cλ.So Φ(U)=0,∀U∈LI.Then Φ must be zero on RIsince LIis the characteristic boundary of RI. □
Remark Theorem 4.1 is just the Riemann jump problem on LI,which is one of the rare examples in several complex variables.
Now we get the main results.
Theorem 4.2 Problem A is solvable if and only if
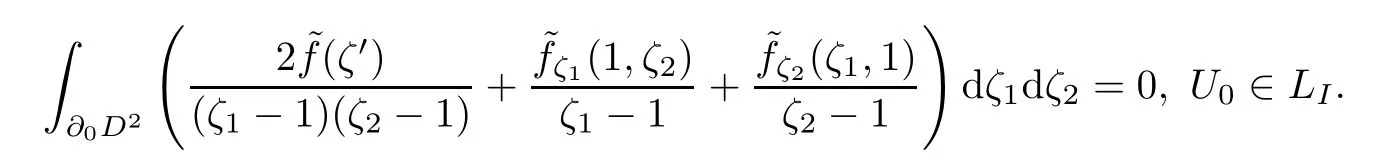
And the solution can be represented by
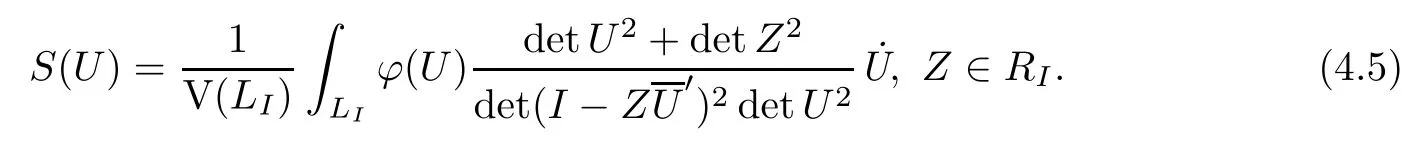
Problem A is one of the simplest Schwarz problems on LI.It is a challenge to discuss them in general.
Problem B Let ϕ(U),A(U)∈Lip1+∈(LI),and ϕ be a real function.Does there exist a function S(U)which is holomorphic in RI(2,2)such that
Acknowledgements The author thanks Professor H.Begehr for his intense advice and help on this problem.He also is in debt to DAAD for a visiting scholarship at the Department of Mathematics and Computer Sciences of FU Berlin from September 2007 to October 2008,where he had worked out most of the topic.
[1]Baouendi M S,Ebenfelt P,Rothschild L P.Real Submanifolds in Complex Space and Their Mappings. New Jersey:Princeton University Press,1999
[2]Begehr H G,Dai D Q.Spatial Riemann problem for analytic functions of two complex variables.J Anal Appl,1999,18:827-837
[3]Begehr H,Dzhuraev A.The Schwarz problem for Cauchy-Riemann systems in several complex variables//Cazacu C A,Lehto O,Rassias Th,eds.Analysis and Topology.Singapore:World Scientific,1998
[4]Begehr H G,Wen G C.Nonlinear Elliptic Boundary Value Problems and Their Applications.London:CRC Press Inc,1996
[5]Guo G A,Du J Y.A class of compound vector-valued problem and factorization of matrix function.Acta Math Sci,2010,30B(1):173-179
[6]Hua L K.Harmonic Analysis of Functions of Several Complex Variables in the Classical Domain.New York:American Mathematical Society,1963
[7]Kakichev V A.Boundary value problems of linear conjugation for functions holomorphic in bicylinderical regions.Soviet Math Dokl,1968,9:222-226
[8]Liu S,Liu H.The Schwarz problem in a Siegel domain.Complex Var Elliptic Equ,2010,55(4):385-394
[9]Lu J K.Boundary Value Problem for Analytic Functions.Singarpore:World Scinetific,1993
[10]Mohammed A.Boundary Value Problems of Complex Variables,Dissertation.Berlin:FU Berlin,2003
[11]Shi J H.Some results on singular integrals and function spaces in several complex variables.Contem Math,1993,142:45-73
[12]Shi J H,Gong S.Singular integral in several complex variables(III).Chinese Ann Math,1983,4B:467-484
[13]Vladimirov V S.Problems of linear conjugacy of holomorphic functions of several complex variables.Trans Amer Math Soc,1969,71:203-232
[14]Vladimirov V S.Methods of the Theory of Many Complex Variables.Cambridge(MA):MIT Press,1966
∗Received March 18,2014;revised February 10,2015.The first author is supported by NSFC(11471250).
 Acta Mathematica Scientia(English Series)2015年5期
Acta Mathematica Scientia(English Series)2015年5期
- Acta Mathematica Scientia(English Series)的其它文章
- ALL MEROMORPHIC SOLUTIONS OF AN AUXILIARY ORDINARY DIFFERENTIAL EQUATION AND ITS APPLICATIONS∗
- APPROXIMATION OF COMMON FIXED POINT OF FAMILIES OF NONLINEAR MAPPINGS WITH APPLICATIONS∗
- SOME COMPLETELY MONOTONIC FUNCTIONS ASSOCIATED WITH THE q-GAMMA AND THE q-POLYGAMMA FUNCTIONS∗
- SUB-ADDITIVE PRESSURE ON A BOREL SET∗
- AN APPLICABLE APPROXIMATION METHOD AND ITS APPLICATION∗
- ORBITAL INSTABILITY OF STANDING WAVES FOR THE GENERALIZED 3D NONLOCAL NONLINEAR SCHR¨ODINGER EQUATIONS∗
