ORBITAL INSTABILITY OF STANDING WAVES FOR THE GENERALIZED 3D NONLOCAL NONLINEAR SCHR¨ODINGER EQUATIONS∗
Zaihui GAN(甘在会)
Center for Applied Mathematics,Tianjin University,Tianjin 300072,China;College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610068,China
Boling GUO(郭柏灵)
Institute of Applied Physics and Computational Mathematics,Beijing 100088,China
Xin JIANG(蒋芯)
College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610068,China
ORBITAL INSTABILITY OF STANDING WAVES FOR THE GENERALIZED 3D NONLOCAL NONLINEAR SCHR¨ODINGER EQUATIONS∗
Zaihui GAN(甘在会)
Center for Applied Mathematics,Tianjin University,Tianjin 300072,China;College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610068,China
E-mail:ganzaihui2008cn@tju.edu.cn;ganzaihui2008cn@hotmail.com
Boling GUO(郭柏灵)
Institute of Applied Physics and Computational Mathematics,Beijing 100088,China
E-mail:gbl@iapcm.ac.cn
Xin JIANG(蒋芯)
College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610068,China
E-mail:jiangxin9099@sina.cn
The existence and orbital instability of standing waves for the generalized threedimensional nonlocal nonlinear Schr¨odinger equations is studied.By defining some suitable functionals and a constrained variational problem,we first establish the existence of standing waves,which relys on the inner structure of the equations under consideration to overcome the drawback that nonlocal terms violate the space-scale invariance.We then show the orbital instability of standing waves.The arguments depend upon the conservation laws of the mass and of the energy.
nonlocal nonlinear Schr¨odinger equations;standing waves;orbital instability 2010 MR Subject Classification 35B35;35J50;35Q55
1 Introduction
In this paper,we study the generalized three-dimensional nonlocal nonlinear Schr¨odinger equations:
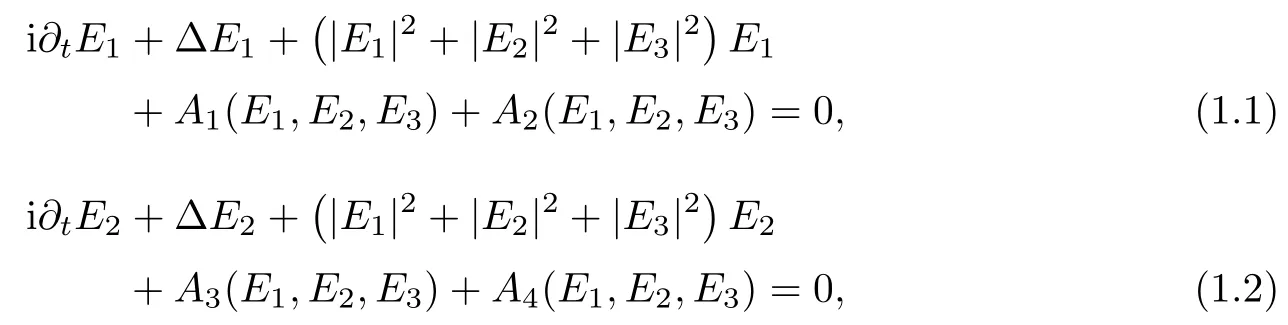

along with the initial data

Here

F and F-1denote the Fourier transform and the Fourier inverse transform,respectively[15,17-19],η>0 and δ≤0 are two constants,(E1,E2,E3)(t,x)are complex vector-valued functions from R+×R3into C3,Ei(i=1,2,3)denotes the complex conjugate of Ei.Due to rotational invariance of(1.1)-(1.3),let E=(E1,E2,E3)and ξ=(ξ1,ξ2,ξ3),system(1.1)-(1.3)is equivalent to a vetor-valued nonlinear Schr¨odinger equations
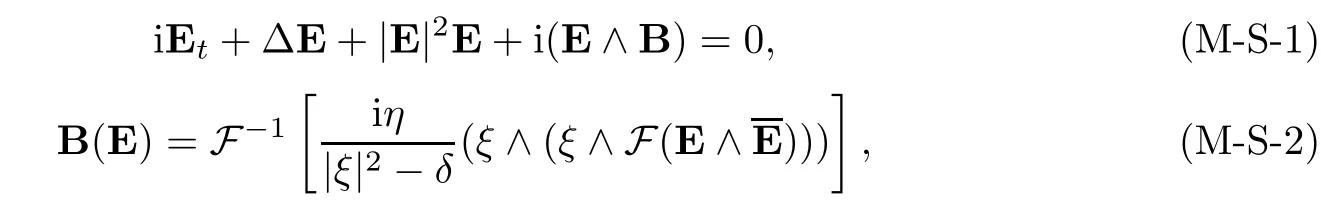
where∧denotes the exterior product of vector-valued functions,and E the complex conjugate of E(indeed,a direct computation implies that equations(1.1)-(1.3)are the componential form of equations(M-S-1)-(M-S-2).To understand the relationship of all the components E1,E2,E3,we adopt the componential form(1.1)-(1.3)in the present paper).
Equations(M-S-1)-(M-S-2)arise in the infinite ion acoustic speed limit of the self-generated magnetic field in a cold plasma,E denotes a slowly varying complex amplitude of the highfrequency electric field,and B the self-generated magnetic field[6,14,27,28].Due to the gauge invariance Aj(eiωtE1,eiωtE2,eiωtE3)=eiωtAj(E1,E2,E3),j=1,2,3,4,5,6,we can study theso-called standing wave solutions of equations(1.1)-(1.3)in the form Ei(t,x)=eiωtui(x)(i= 1,2,3)with the initial condition(1.4),where ω>0 is a real constant parameter called frequency and ui(x)(i=1,2,3)is a complex-valued function.The search for standing waves of equations(1.1)-(1.3)leads to the following nonlinear elliptic equations(1.5)-(1.7):

For the nonlinear Schr¨odinger equations without any nonlocal term,there were many works on the stability results of their standing waves.Berestycki and Cazenave[1],Grillakis[10],Jones[13],Shatah and Strauss[20],Weinstein[23]and Zhang[26]investigated the instability of solitons.On the other hand,Cazenave and Lions[4],Weinstein[24],Grillakis,Shatah and Strauss[11]studied the stability of the standing waves.Some other topics for the nonlinear Schr¨odinger equations without any nonlocal term were studied(see for example[5,16,22,25]).
In the study of equations(1.1)-(1.3),we still concentrate on the existence and orbital instability of the standing waves.For the nonlocal nonlinear Schr¨odinger equations,to our best knowledge,there have been no any works on the existence and instability of the standing waves other than those in our former papers[7-9],where we studied the similar topic for a general Davey-Stewartson system[7]and a simplified version for the nonlocal nonlinear Schr¨odinger equations(1.1)-(1.3)[8,9],in which(E1,E2,E3)=(E1,E2,0),(ξ1,ξ2,ξ3)=(ξ1,ξ2,0).To attain our goal in the present paper,the main difficulty is to deal with the nonlocal terms since the nonlocal terms may violate the space inner-scale invariance,and we are forced tomake some additional arguments for them.Fortunately,by defining some suitable functionals and a constrained variational minimization problem,utilizing the monotonicity argument for some defined auxiliary functions to deal with these terms generated by the nonlocal effects,and applying the inner structure of the corresponding elliptic equations(1.5)-(1.7),we first show the existence of standing waves for equations(1.1)-(1.3).In addition,we establish the orbital instability of the standing waves for the equations under consideration.The arguments of the result rely on the conservation of energy and mass as well as the construction of a suitable invariant manifold of solution flows.However,it should be pointed out that the uniqueness of these ground states for(1.5)-(1.7)is a much different and difficult problem,and we do not intend to discuss it in the present paper.
This paper arranges as follows.In Section 2,we give some preliminaries and state the main results.The existence of standing waves with ground states will be established in Section 3.At the last section,we will show the orbital instability of standing waves.
For simplicity,we denote any positive constant by C throughout the present paper.
2 Preliminaries and Main Results
In this section,we first establish the conservation laws of the total mass and of the total energy.Then we define some functionals,a set and a constrained variational minimization problem.At the end of this section we state the main results of this paper.
2.1 Conservation Laws of the Mass and of the Energy
According to the inner structure of equations(1.1)-(1.3),making some estimates on the nonlocal terms and using the standard contraction mapping theorem,we can establish the local well-posedness in the energy space H1(R3)×H1(R3)×H1(R3),the conservation laws of the total mass and of the total energy for the Cauchy problem(1.1)-(1.4).
Lemma 2.1 The Cauchy problem(1.1)-(1.4),for η>0,δ≤0 and
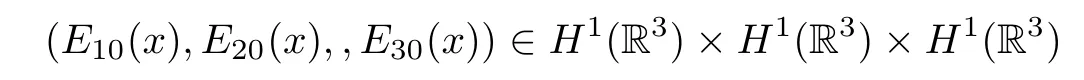
has a unique solution
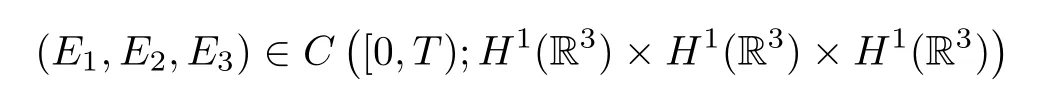
for some T∈(0,+∞)with T=+∞or T<+∞and
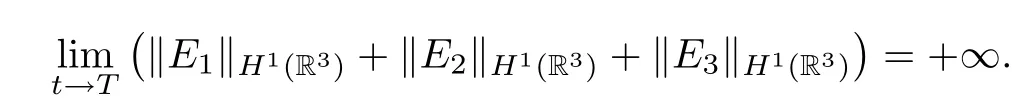
In addition,the total mass and total energy are conserved:
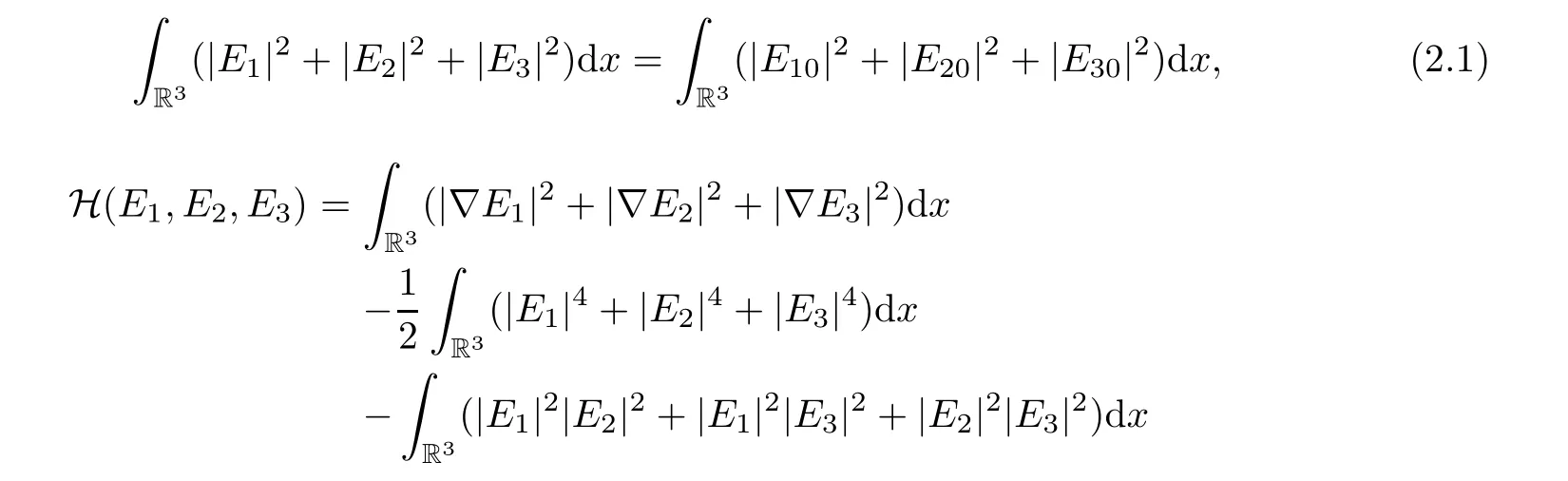
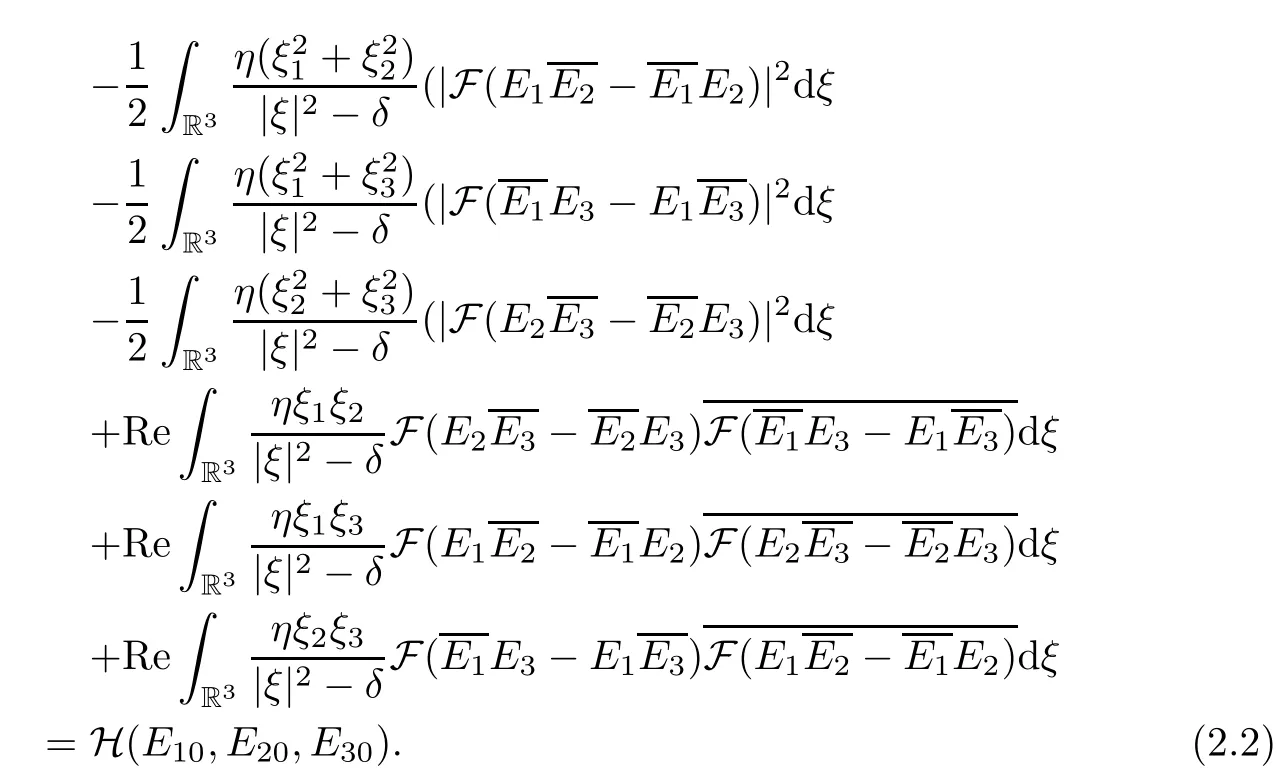
To attain the conservation identities(2.1)and(2.2),besides using the standard arguments on the nonlinear Schr¨odinger equations without any nonlocal terms,we must give some extra discussions on the nonlocal terms,in which we will employ the Parseval identity,some properties of Fourier transform,suitable groupings and potential coupled arguments for these nonlocal terms.In Lemma 2.1 of[12],we established the detail of the proof for(2.1)and(2.2).
2.2 Variational Structures
For(u1,u2,u3)∈H1r(R3)×H1r(R3)×H1r(R3)(ui(x)(i=1,2,3)is a complex-valued function),we define the following functionals:
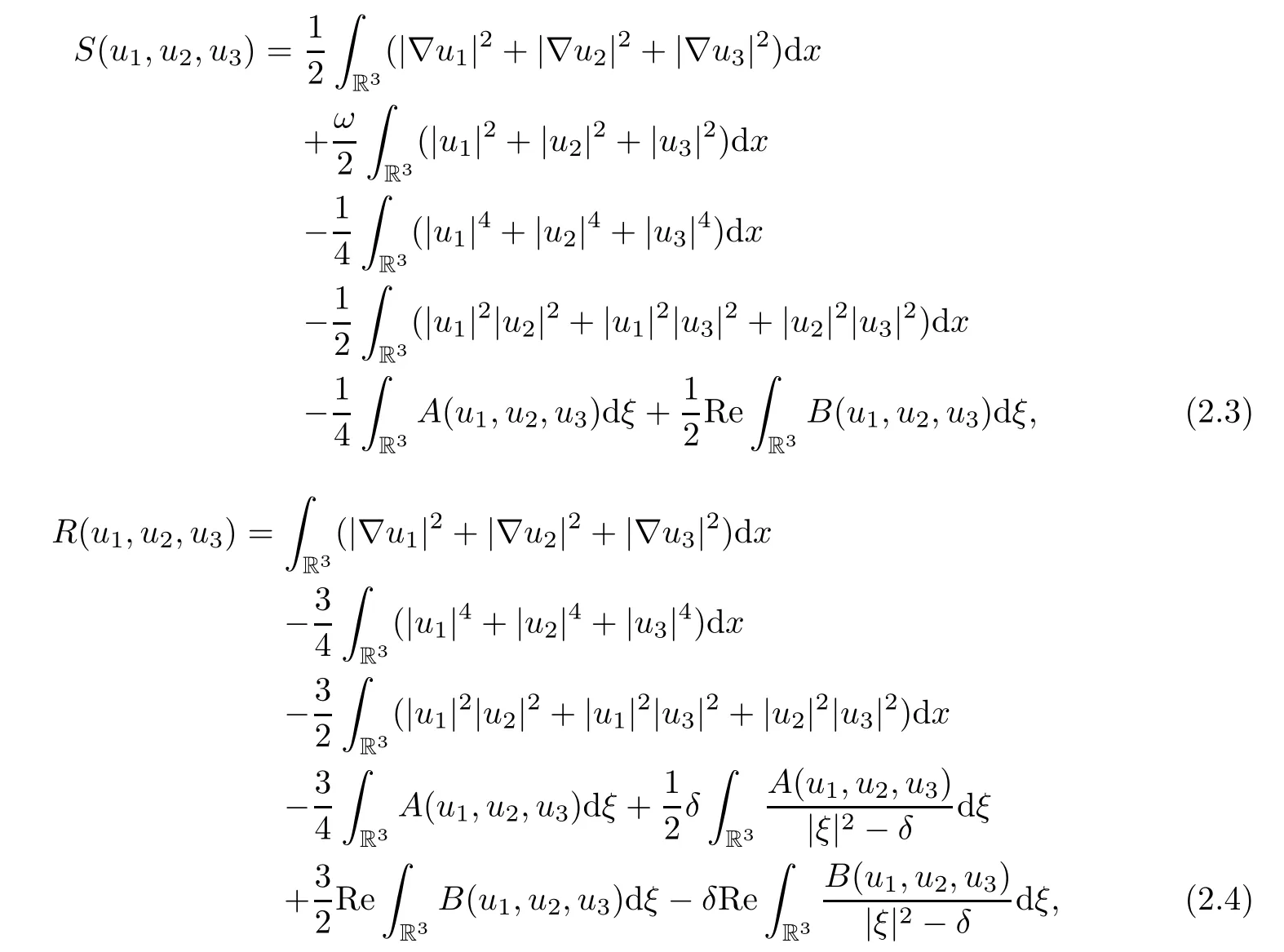
where
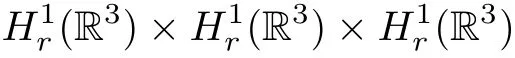
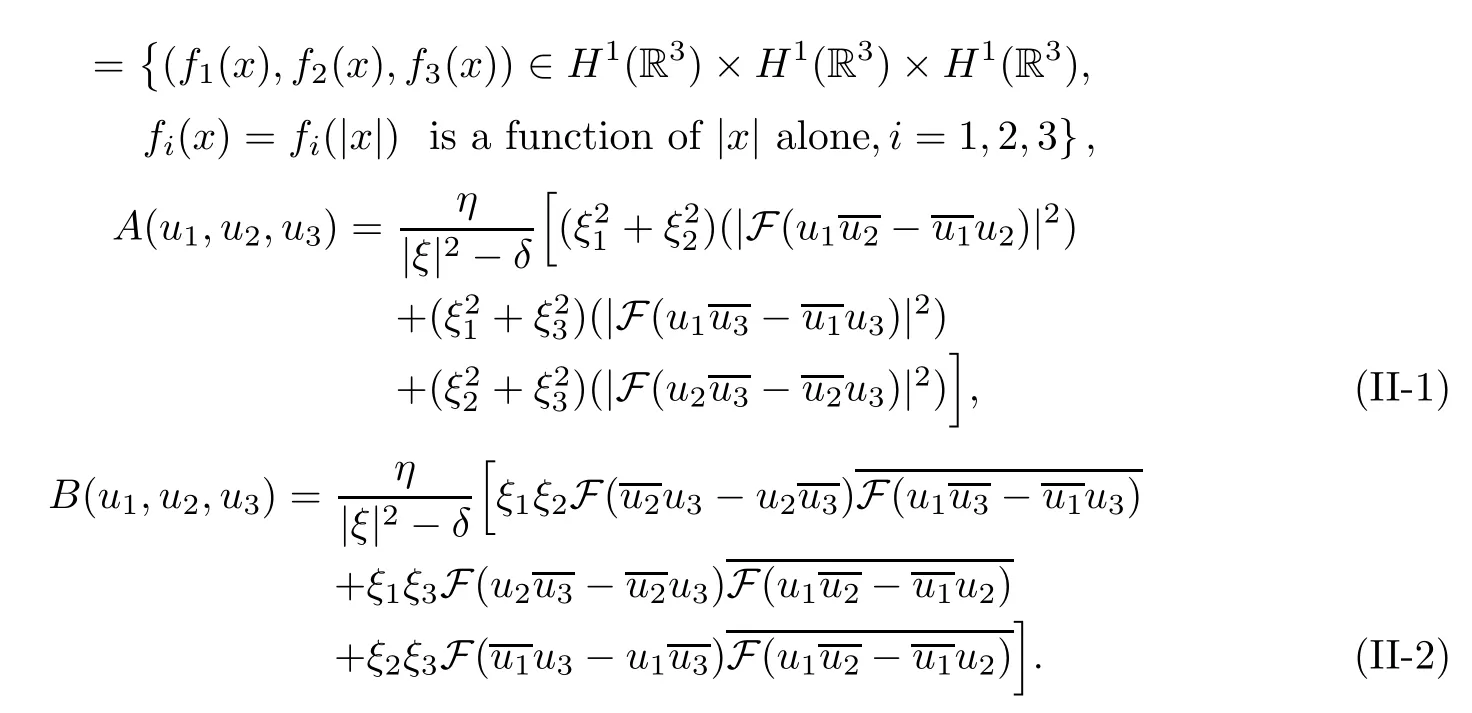
A natural attempt to find nontrivial solutions to(1.5)-(1.7)is to solve the constrained minimization problem
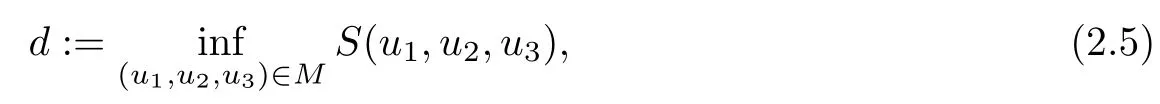
where the set M is defined by
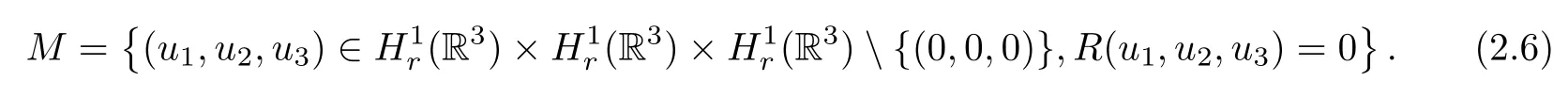
From(u1,u2,u3)∈H1r(R3)×H1r(R3)×H1r(R3),η>0,δ≤0,the Sobolev's embedding theorem and the properties of Fourier transform,it follows that functionals S(u1,u2,u3)and R(u1,u2,u3)are both well defined.
Remark 2.1 We note that for all θ≥1,j,k,l,m=1,2,3,
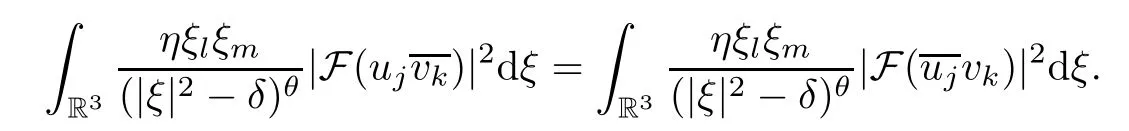
We also note that if(u1,u2,u3)is a critical point of S(u1,u2,u3)and hence a solution of(1.5)-(1.7),then(E1,E2,E3)=(eiωtu1,eiωtu2,eiωtu3)is a standing wave solution of(1.1)-(1.3).
2.3 Main Results
Here,we state the main results of this paper.
Theorem 2.1 For η>0 and δ≤0,there exists(Q1,Q2,Q3)∈M such that

(2)(Q1,Q2,Q3)is a ground state solution to(1.5)-(1.7).
(3)(Q1,Q2,Q3)are functions of|x|alone and decay exponentially at infinity.
From the physical viewpoint,an important role is played by the ground state solution of(1.5)-(1.7).A solution(Q1,Q2,Q3)to(1.5)-(1.7)is termed as a ground state if it has some minimal action among all solutions to(1.5)-(1.7).Here,the action of solution(u1,u2,u3)is defined by S(u1,u2,u3).
Concerning the dynamics of the ground state solution(Q1,Q2,Q3),we have the following orbital instability result.Here,we assume that the ground state solution(Q1,Q2,Q3)of(1.5)-(1.7)is unique.
Theorem 2.2 For η>0 and δ≤0,let(Q1,Q2,Q3)∈M be given by Theorem 2.1.For arbitrary ε>0,there exists(E10,E20,E30)∈H1r(R3)×H1r(R3)×H1r(R3)withsuch that the solution(E1,E2,E3)of equations(1.1)-(1.3)with the initial data(1.4)has the following property:For some finite time T<∞,(E1,E2,E3)exists on[0,T),(E1,E2,E3)∈C([0,T);H1r(R3)×H1r(R3)×H1r(R3))and
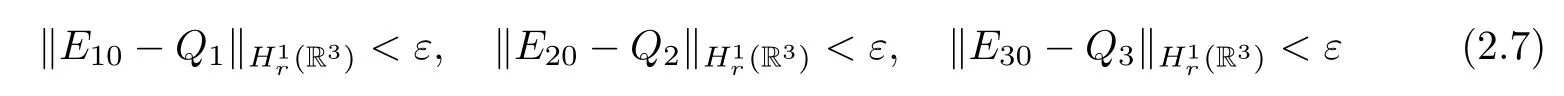
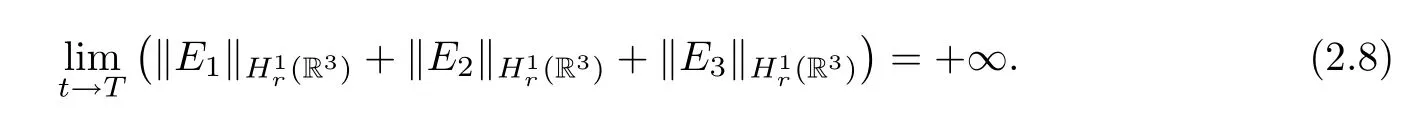
3 Existence of Standing Waves
In this section,we prove Theorem 2.1,which concerns the existence of minimal energy standing waves of system(1.1)-(1.3).For that purpose,we first give some key propositions and lemmas.
Remark 3.1 For η>0,δ≤0,θ=1,2,j,k,l,m=1,2,3,since
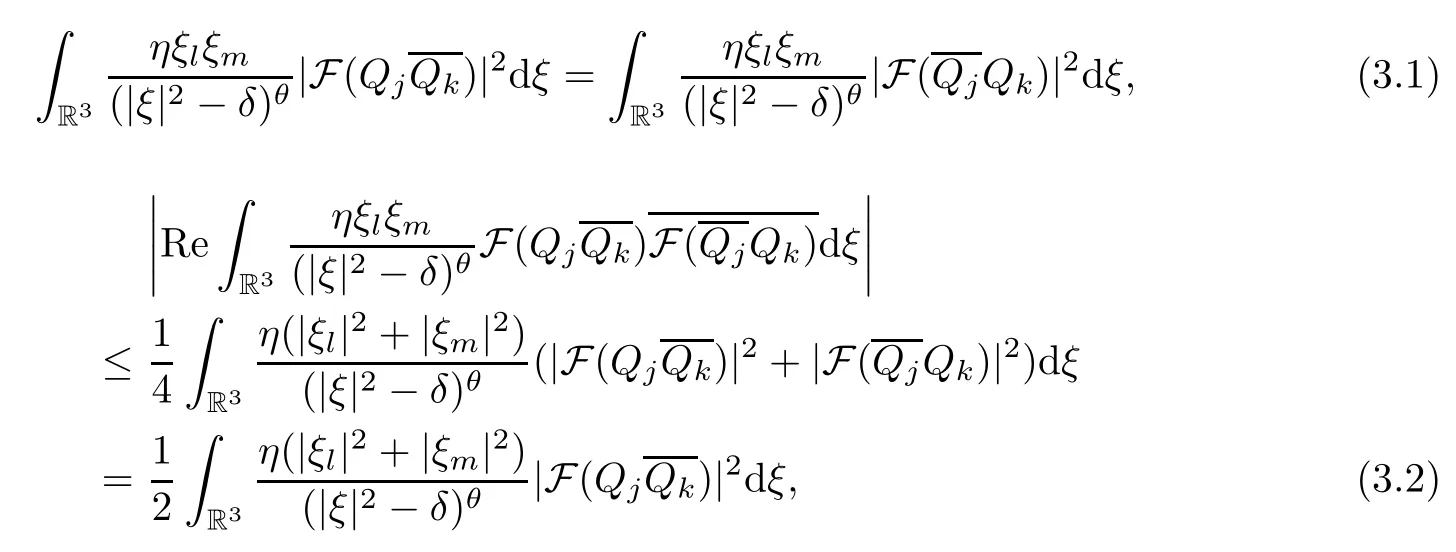
by Theorem 2.1,(2.3),(2.4)and(2.5),one has
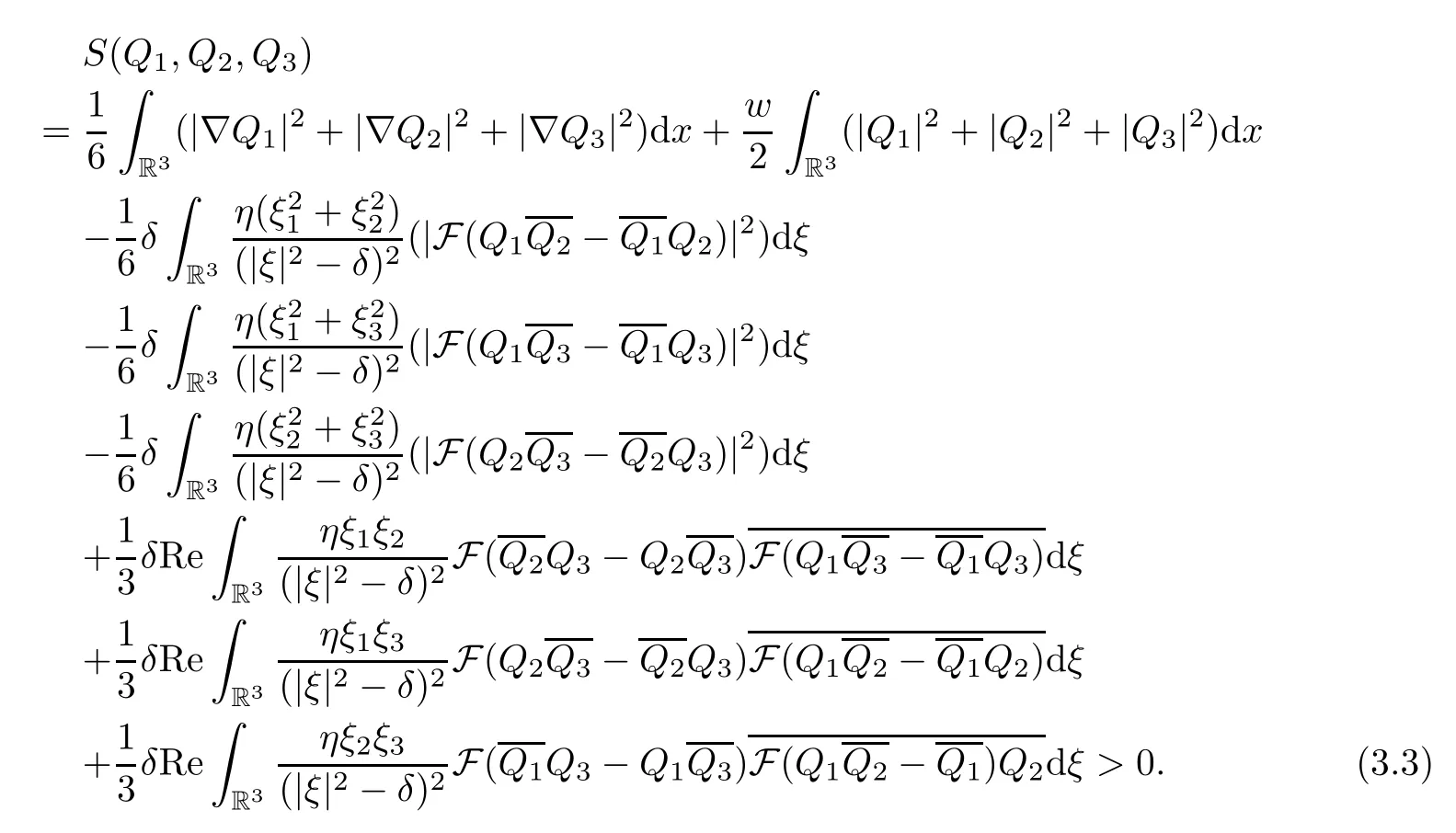
We continue to give some key facts.
Lemma 3.1[21,23]For 2<σ<6,the embedding H1r(R3)→Lσr(R3)is compact,where
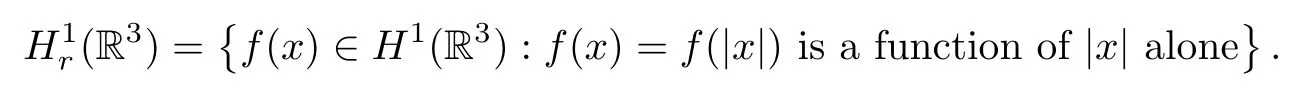
Proposition 3.1 Let η>0 and δ≤0.Then the non-trivial solution to(1.5)-(1.7)belongs to M.
Proof Let(u1,u2,u3)be a non-trivial solution to(1.5)-(1.7).Multiplying(1.5)bythen integrating with respect to x on R3,we obtain
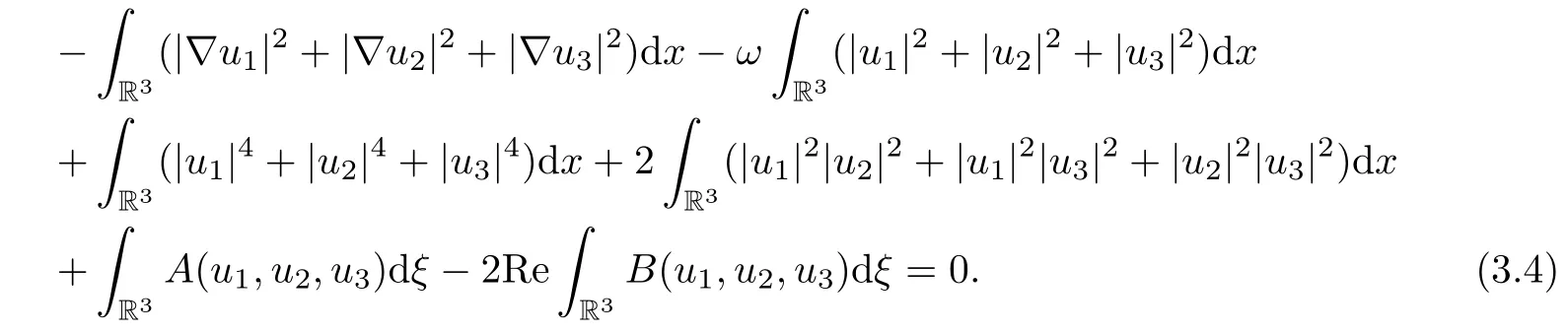
We further attain the following identity:

here A and B are defined by(II-1)and(II-2)in Section 2,respectively.Identity(3.5)is obtained by multiplying(1.5)bythen integrating with respect to x in R3and taking the real parts for the resulting equations,finally using the following estimates:Combining(3.4)with(3.5),one can easily verifies that R(u1,u2,u3)=0,and hence(u1,u2,u3)∈M. □
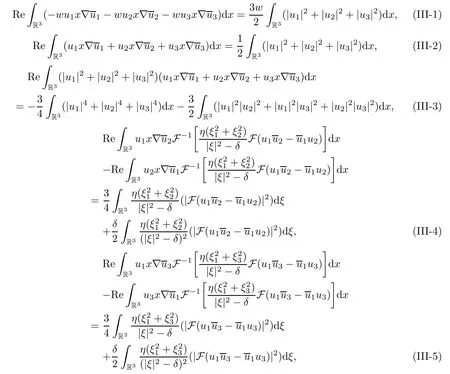

Proposition 3.2 The functional S is bounded from below on M for η>0 and δ≤0.
Proof Let A and B are defined by(II-1)and(II-2)in Section 2,respectively.According to(2.3),(2.4)and(2.6),for(u1,u2,u3)∈M one gets
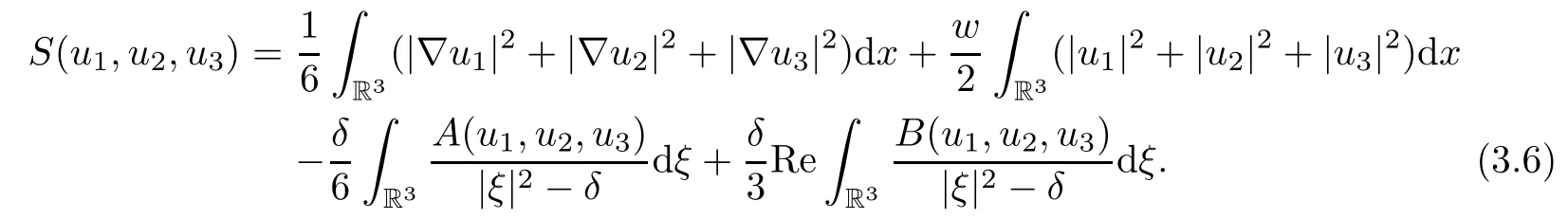
Noting that η>0,δ≤0 and the inequality 2Re(ab)≤a2+b2,making some suitable rearrangements,we obtain
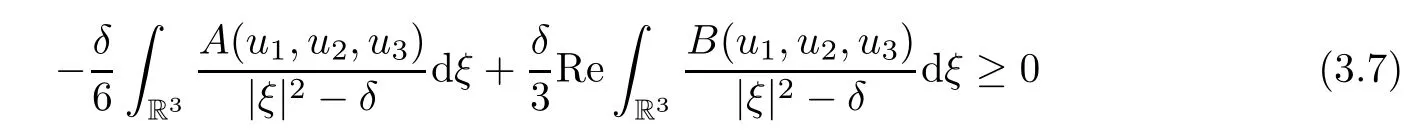
(indeed,recall that

Since

through regrouping and applying some properties of Fourier transform,we conclude that for η>0,and δ≤0,
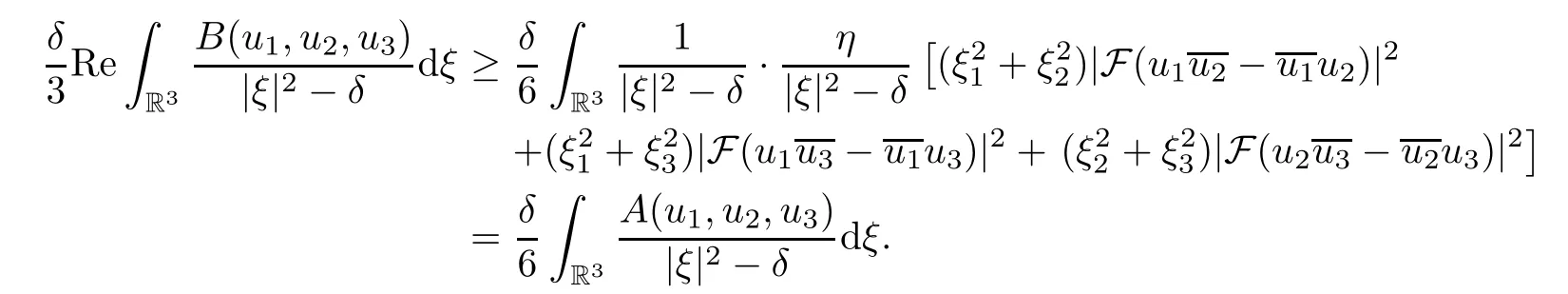
Hence(3.7)is valid).
Therefore,(3.6)and(3.7)imply that on M,
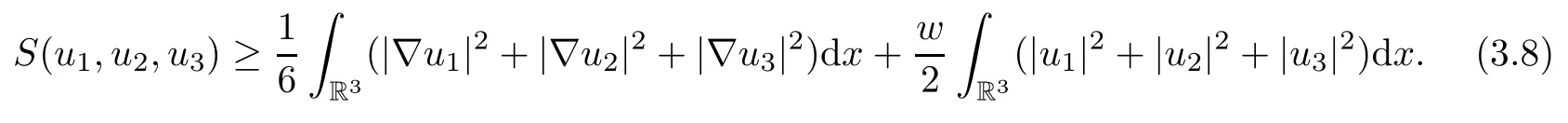
This completes the proof of Proposition 3.2. □
Proposition 3.3 For η>0 and δ≤0,let(u1,u2,u3)∈H1r(R3)×H1r(R3)×H1r(R3){(0,0,0)}.For λ>0,we make the following scale transform:
then there exists a uniqueµ> 0(relying on(u1,u2,u3))such that R(u1µ,u2µ,u3µ)=0. Furthermore,the following three estimates will occur:
Proof According to(2.3)and(2.4),S(u1λ,u2λ,u3λ)and R(u1λ,u2λ,u3λ)are of the following expressions:

Making a preliminary estimate,we can verify that((3.11)can be easily obtained by utilizing the method of verifying(3.7)).

First of all,we show that there existsµ>0 such that R(u1µ,u2µ,u3µ)=0,and we divide the proof into two cases:
Case 1 R(u1,u2,u3)>0;
Case 2 R(u1,u2,u3)<0.
If Case 2 occurs,and if there exists λ such that R(u1λ,u2λ,u3λ)=0,then λ∈(0,1).Indeed,we consider functional R∗(u1λ,u2λ,u3λ)defined by(3.10).Note that R∗(u1λ,u2λ,u3λ)→R(u1,u2,u3)<0 as λ→1,and R∗(u1λ,u2λ,u3λ)=RR3(|∇u1|2+|∇u2|2+|∇u3|2)dx>0 as λ→0,one can verifies that there existsµ∈(0,1)such that R∗(u1µ,u2µ,u3µ)=0.The latter implies thatµ2R∗(u1µ,u2µ,u3µ)=R(u1µ,u2µ,u3µ)=0.
In both cases as above,there always existsµ>0 such that R(u1µ,u2µ,u3µ)=0.
Furthermore,we can easily check that
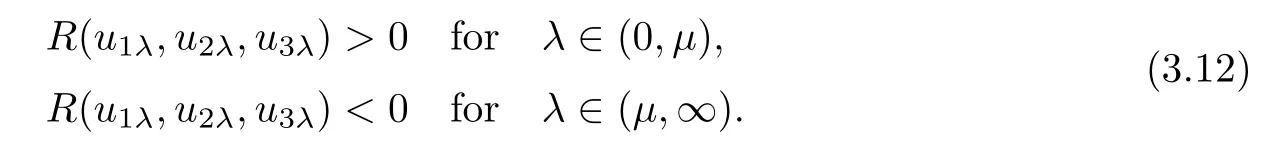
By a direct calculation,we achive for j,k=1,2,3,
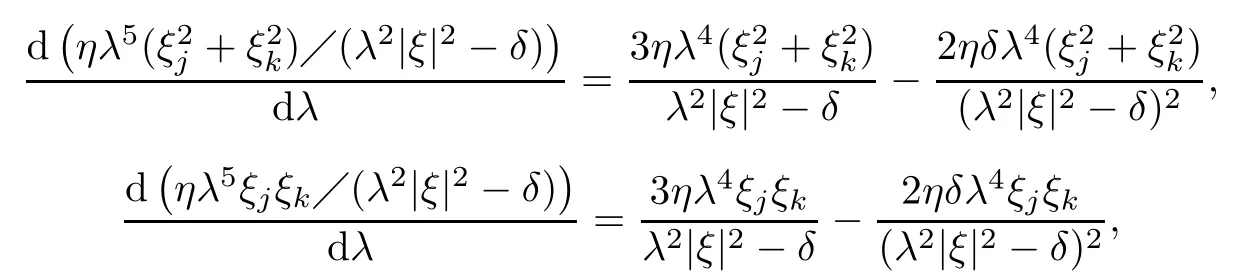
which together with(3.9)and(3.10)yield that
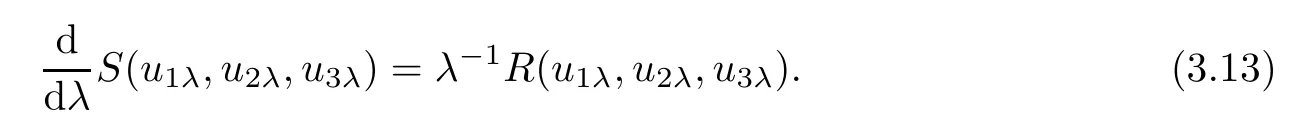
By R(u1µ,u2µ,u3µ)=0,(3.12)and(3.13)imply that
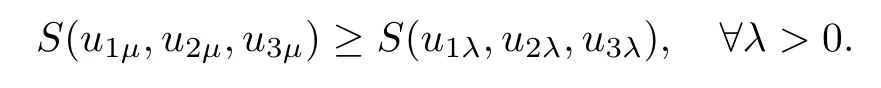
This completes the proof of Proposition 3.3.
Now,we begin to prove Theorem 2.1.
Step 1 Proof of(1).
Let{(Q1n,Q2n,Q3n),n∈N}⊂M be a minimizing sequence for(2.5).There then has
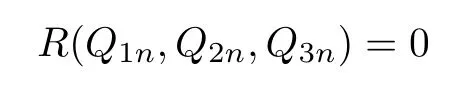
and
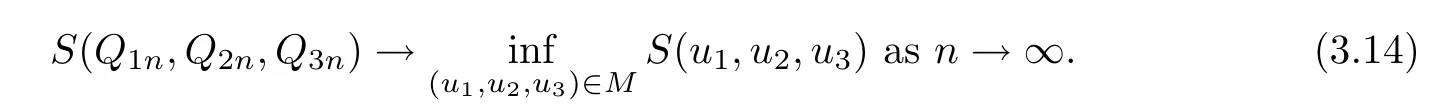
In view of η> 0,δ≤ 0 and Young's inequality,combining(3.6)with(3.14)yields that‖Q1n‖H1r(R3),‖Q2n‖H1r(R3),‖Q3n‖H1r(R3)are all bounded for all n∈N.Thus there exists a subsequence
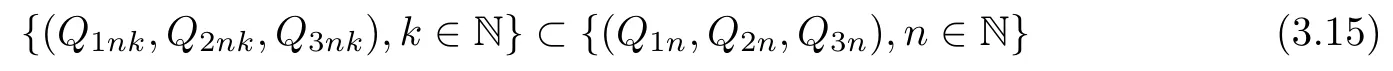
such that as k→∞,
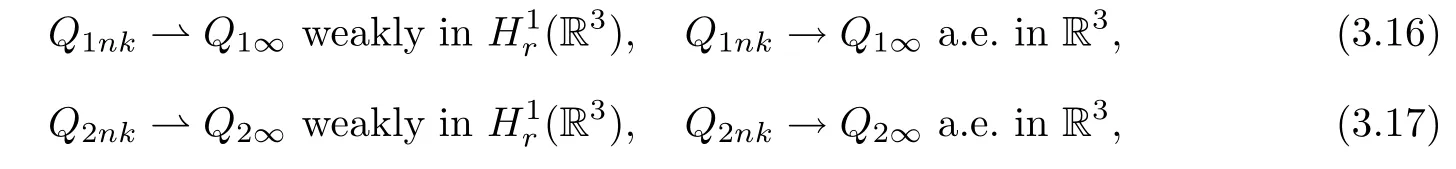
and
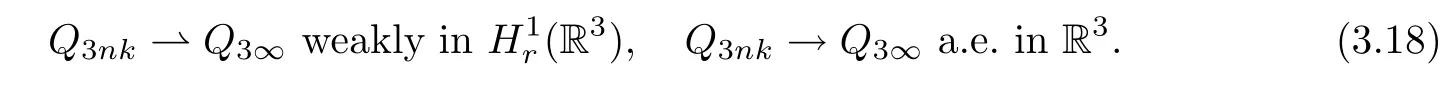
For simplicity,we still denote{(Q1nk,Q2nk,Q3nk),k∈N}by{(Q1n,Q2n,Q3n),n∈N}.From Lemma 3.1,(3.16)-(3.18),it follows that
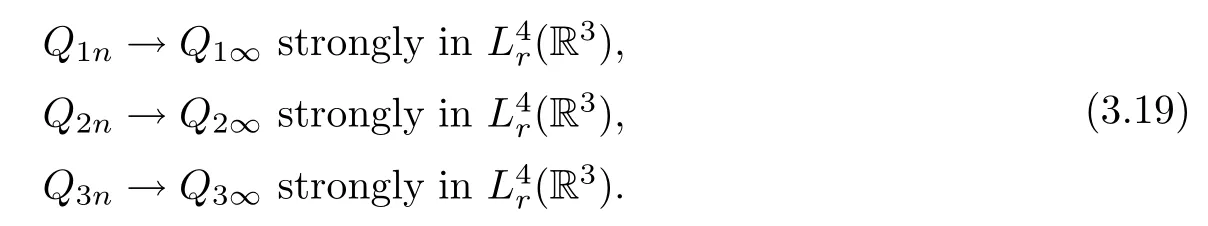
Since
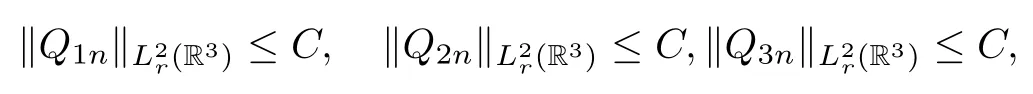
the boundedness of{(Q1n,Q2n,Q3n),n∈N}in H1r(R3)×H1r(R3)×H1r(R3)and the Gagliardo-Nirenberg inequality
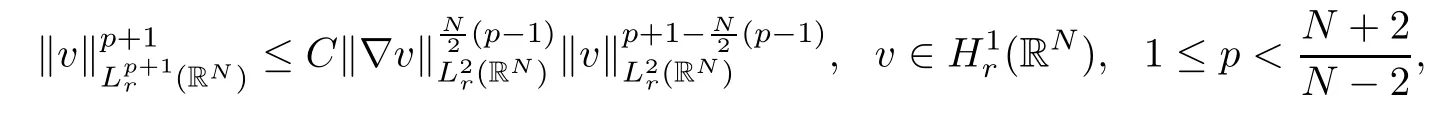
imply in particular that
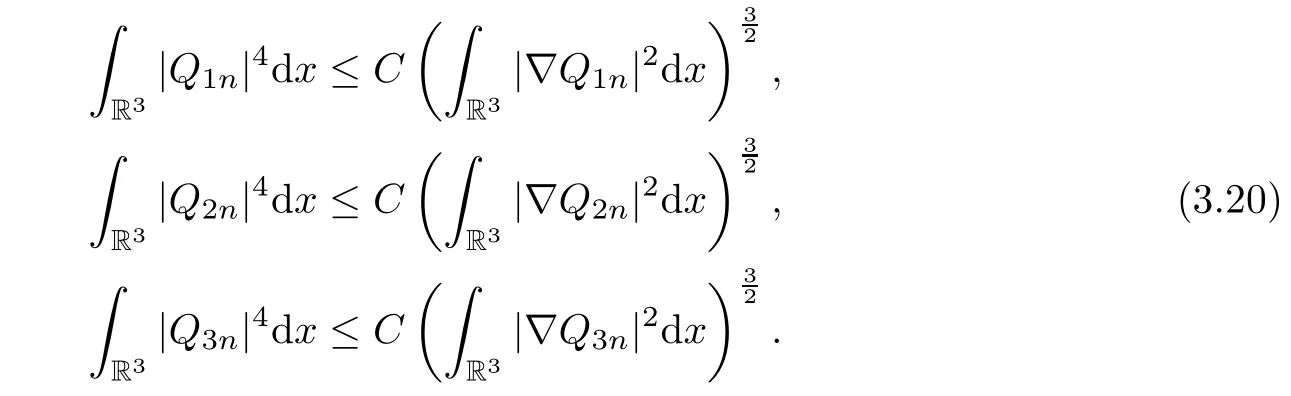
Here and henceforth,C>0 denotes various positive constants.Via(3.20),η>0,δ≤0 and

where j,k=1,2,3,we thus obtain
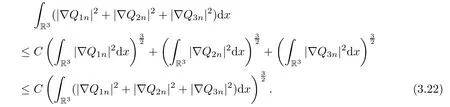

Thus,(3.21)implies that as n→∞,
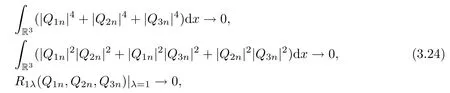
where R1λ(Q1n,Q2n,Q3n)is defined by(3.10)with replacing(u1,u2,u3)by(Q1n,Q2n,Q3n). In view of R(Q1n,Q2n,Q3n)=0,one would then conclude that as n→∞,
Z
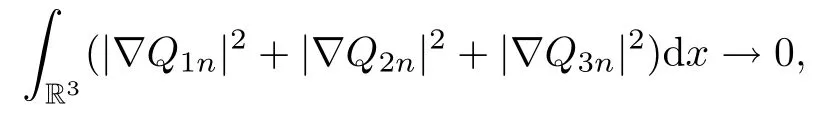
which contradicts to(3.22).Thus(Q1∞,Q2∞,Q3∞)/=(0,0,0).
Let Q1=(Q1∞)µ,Q2=(Q2∞)µ,Q3=(Q3∞)µwithµ>0 uniquely determined by the condition R(Q1,Q2,Q3)=R[(Q1∞)µ,(Q2∞)µ,(Q3∞)µ]=0,where(Q1∞)µ,(Q2∞)µand(Q3∞)µare defined by Proposition 3.3.Thus Lemma 3.1 yields that,as n→∞,
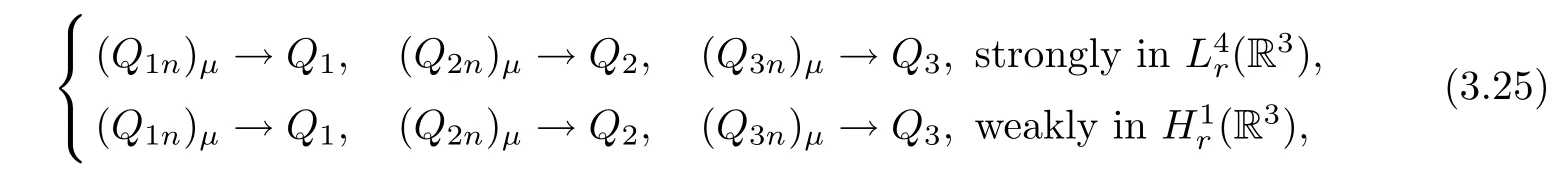
whereas R(Q1n,Q2n,Q3n)=0 and Proposition 3.3 imply
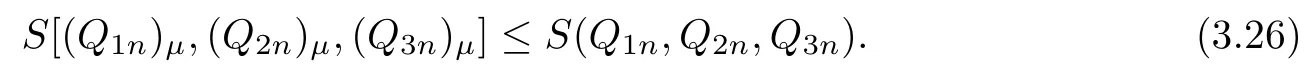
Hence,from(3.25)and(3.26)one concludes
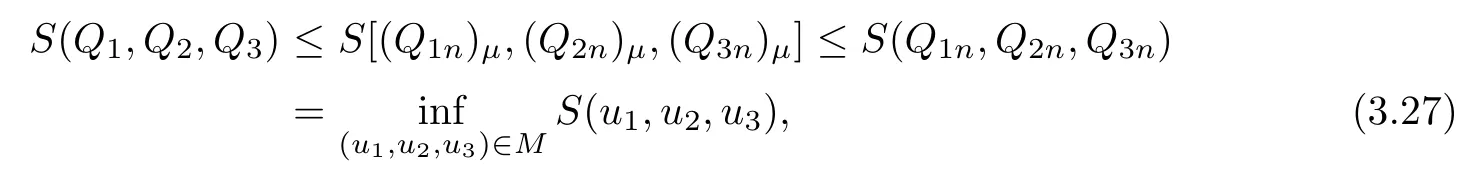
which together with R(Q1,Q2,Q3)=0 yields that(Q1,Q2,Q3)∈M.Therefore,(Q1,Q2,Q3)solves the minimization problem

This completes the proof of(1)of Theorem 2.1.
Step 2 Proofs of(2)and(3)of Theorem 2.1
We first prove(2).Since(Q1,Q2,Q3)is a solution of the minimization problem(3.28),there exists a Lagrange multiplier Λ such thathere δ′u1T(u1,u2,u3)denotes the variation of T(u1,u2,u3)with respect to u1.By the formulaand by takingandwe obtain from(3.29)that
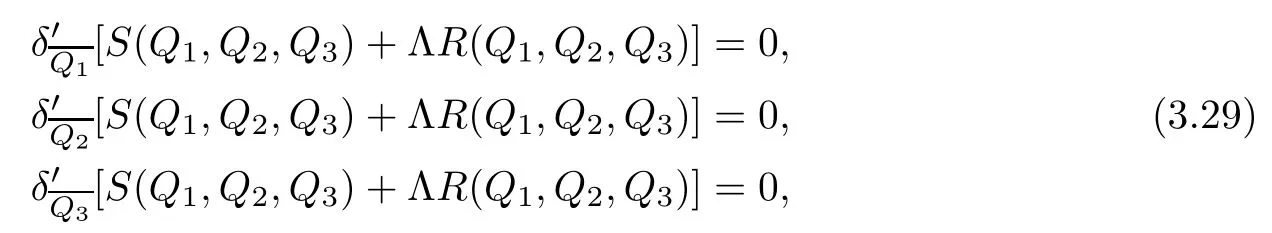
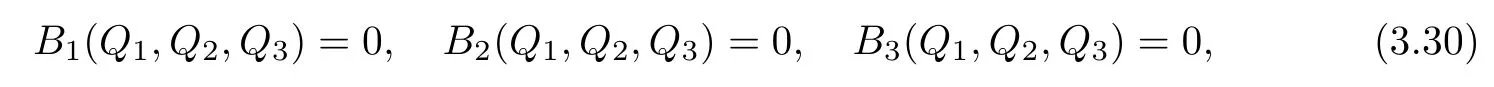
where
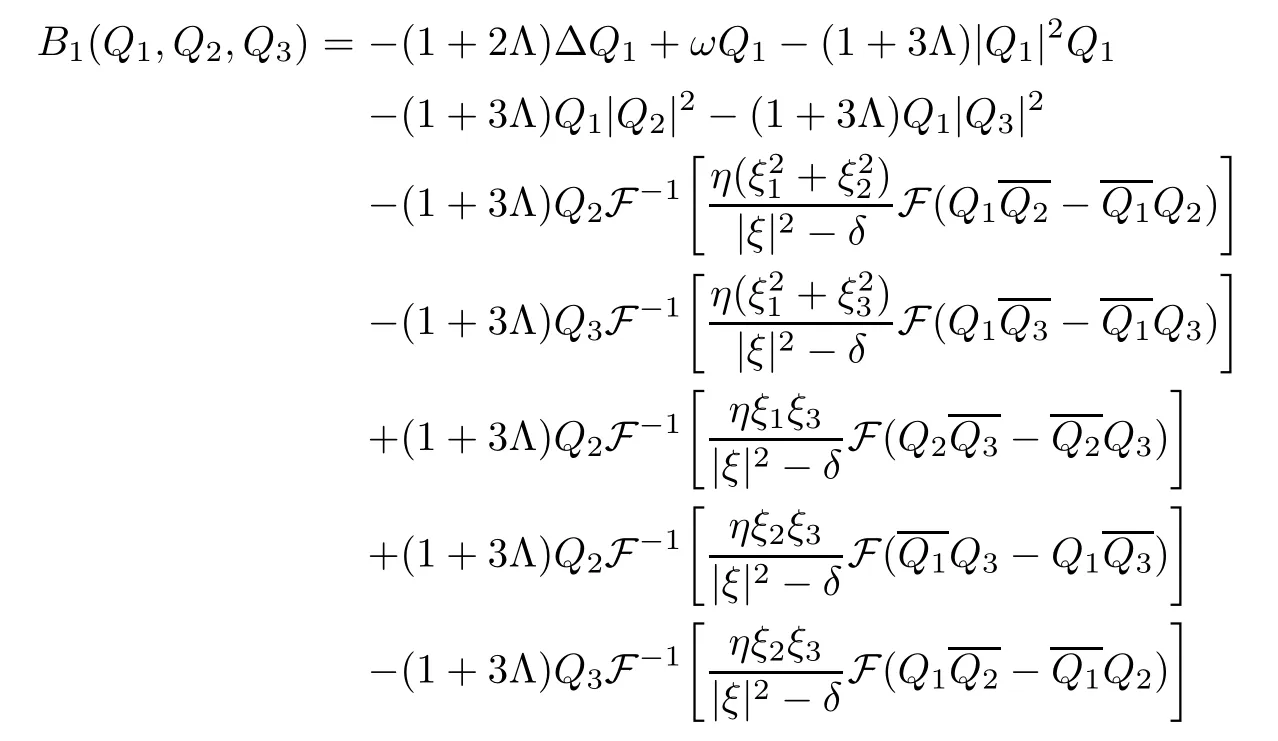


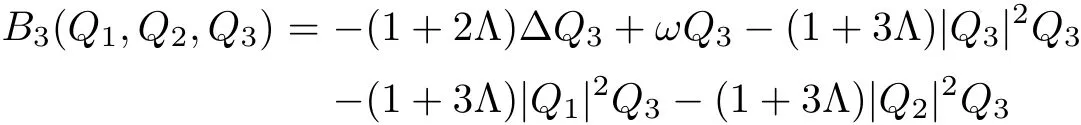

Multiplying B1(Q1,Q2,Q3)=0 by Q1,B2(Q1,Q2,Q3)=0 by Q2and B3(Q1,Q2,Q3)=0 bythen integrating the resulting equations with respect to x on R3,we get
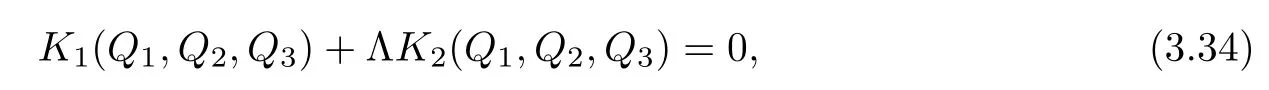
where
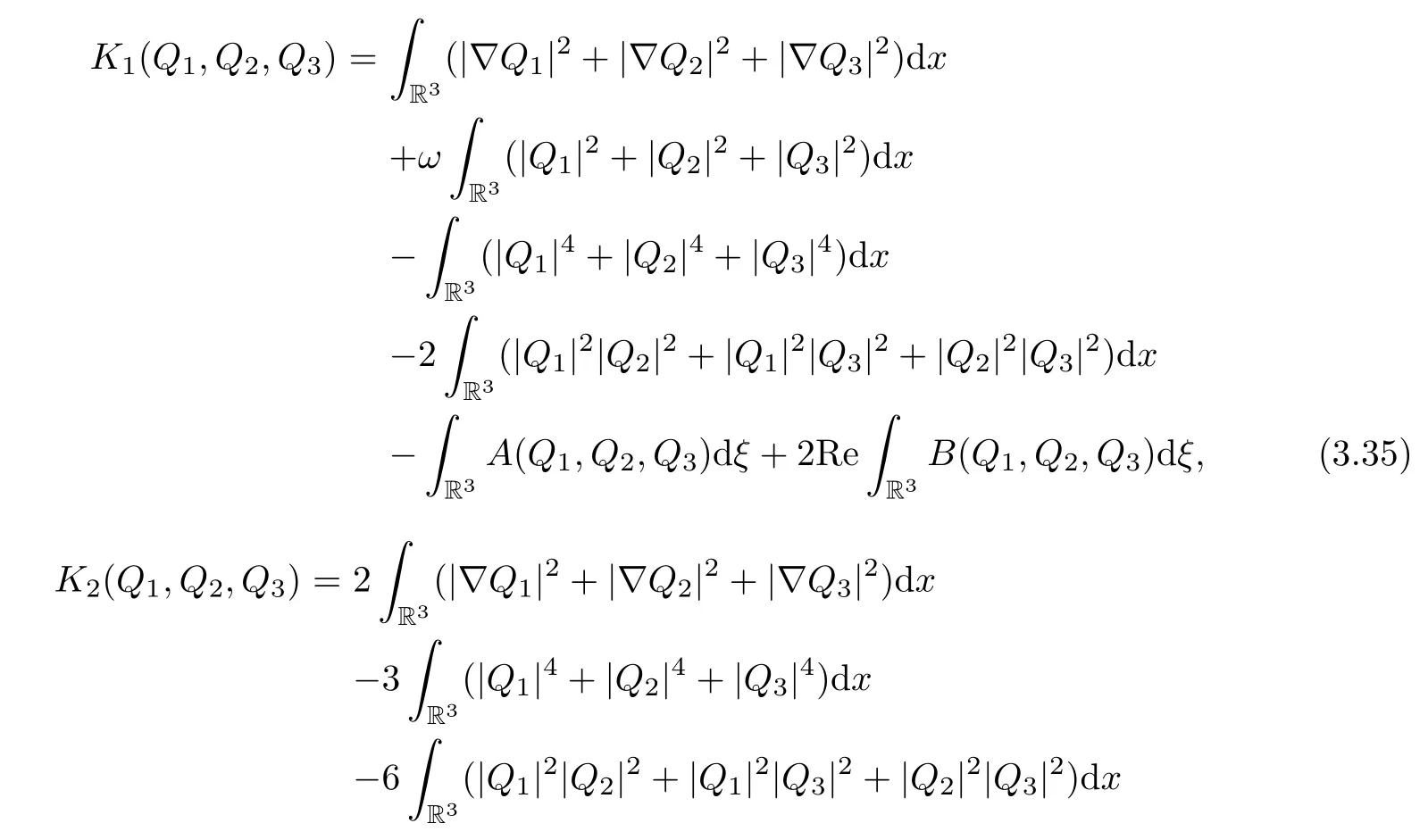
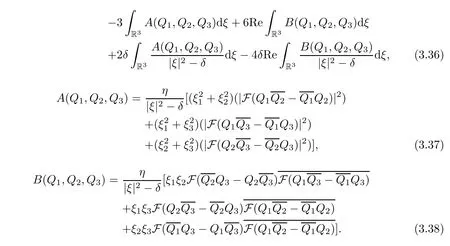
On the other hand,multiplyingbythen integrating the resulting equations with respect to x on R3and taking the real part,one obtains
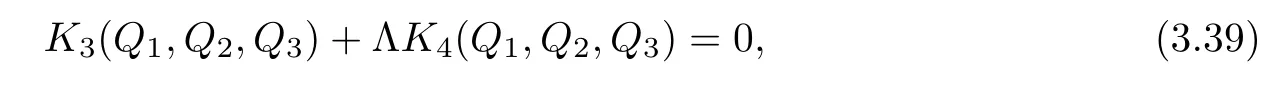
where

here A(Q1,Q2,Q3)and B(Q1,Q2,Q3)are defined by(3.37)and(3.38),respectively.Thus by(3.34),we obtain
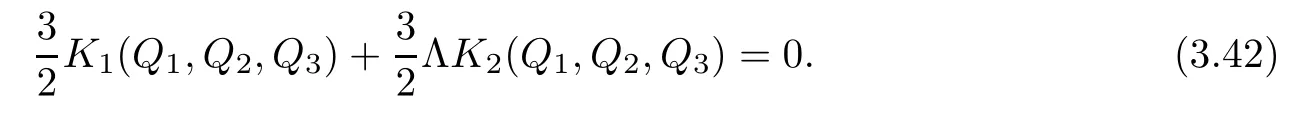
Noting that
in view of(3.39),(3.42),(3.43),one can verify that
(3.44)is equivalent to
where
Noting the expressions of A(Q1,Q2,Q3)and B(Q1,Q2,Q3)in(3.37)and(3.38),applying the Young's inequality,we have
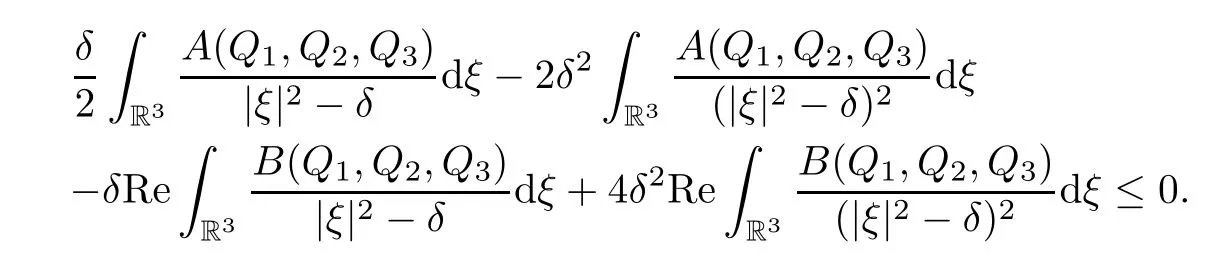
Then,in view of(Q1,Q2,Q3)/=(0,0,0),R(Q1,Q2,Q3)=0,η>0 and δ≤0,there holds

which implies that K5(Q1,Q2,Q3)/=0 and thus Λ=0 by(3.45).Hence,from(3.30),(3.31),(3.32)and(3.33),it follows that(Q1,Q2,Q3)solves the following equations:
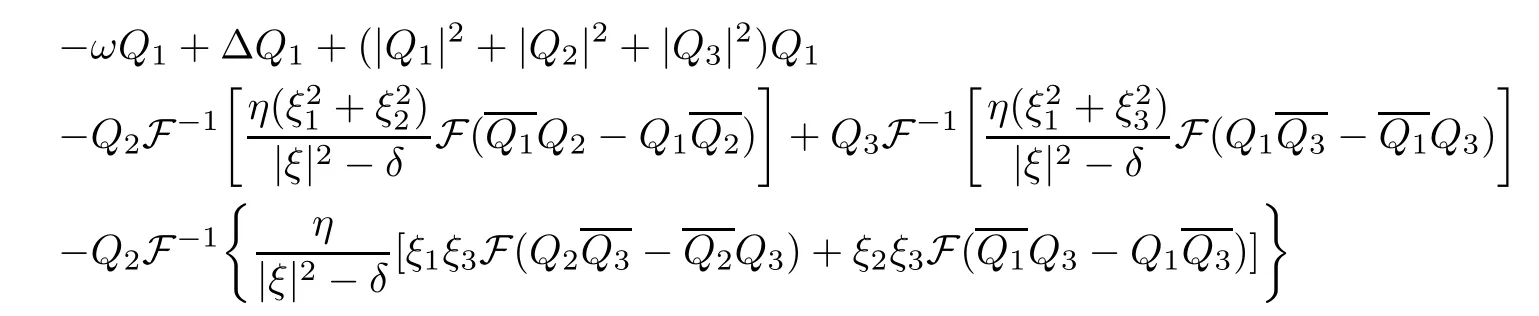
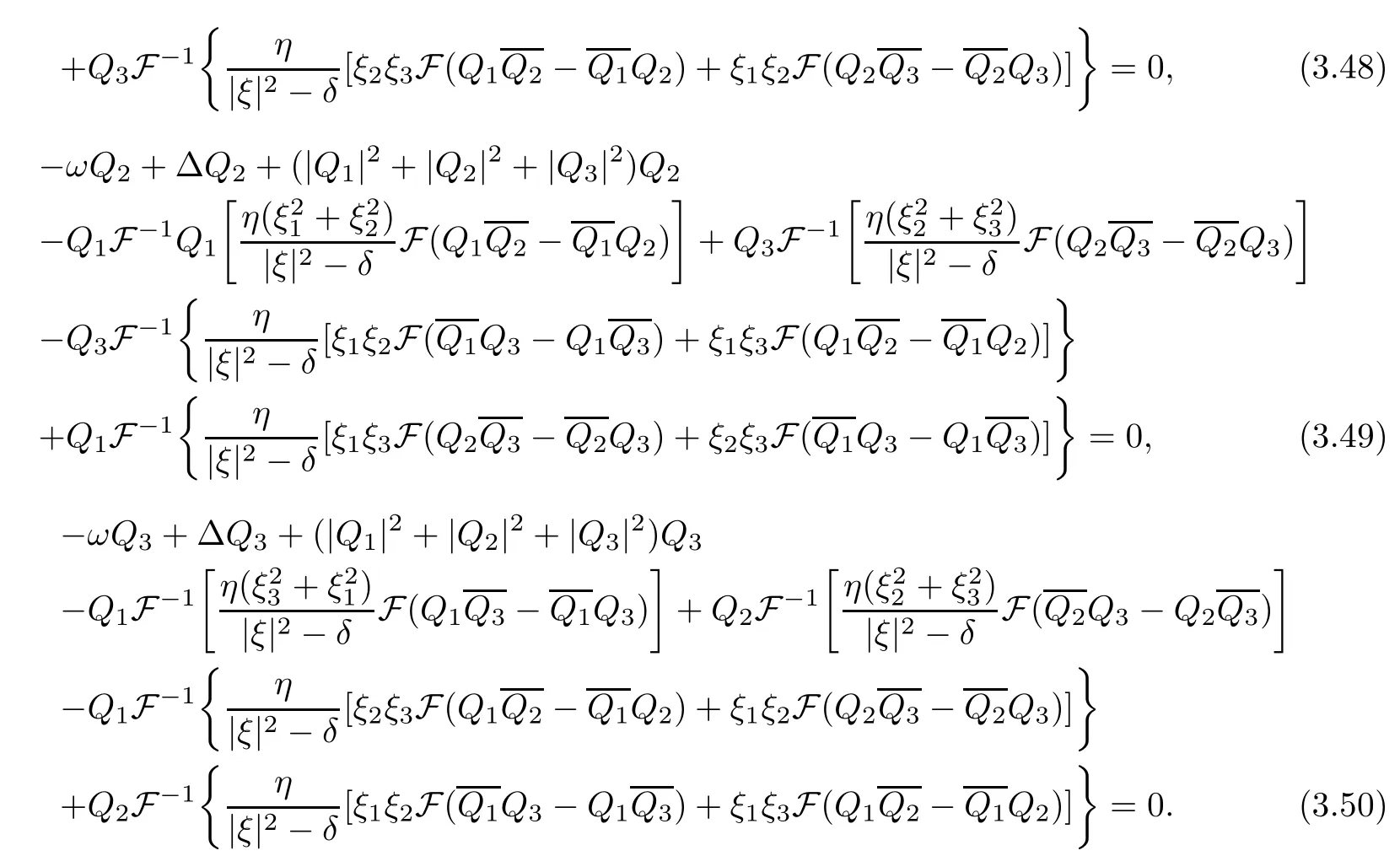
That is,(Q1,Q2,Q3)solves equations(1.5)-(1.7).As(1.5)-(1.7)are the Euler-Lagrange equations of the functional S(Q1,Q2,Q3),applying Proposition 3.1,we conclude(Q1,Q2,Q3)is a ground state solution of(1.5)-(1.7).Furthermore,it is obvious that(Q1,Q2,Q3)are functions of|x|alone.Motivated by the works[2,3],we can obtain that(Q1,Q2,Q3)has exponential decay at infinity,which will be shown in the Appendix A for convenience.
This completes the proof of Theorem 2.1.
4 Orbital Instability of Standing Waves in R3
In this section,we show the instability of standing waves of(1.1)-(1.3)in R3obtained in Theorem 2.1(Theorem 2.2).We first give a key proposition to show Theorem 2.2.
Proposition 4.1 Let δ≤0,η>0 and u1λ(x)=λ32u1(λx),u2λ(x)=λ32u2(λx),u3λ(x)= λ32u3(λx)for λ>0.Suppose that(u1,u2,u3)∈H1r(R3)×H1r(R3)×H1r(R3){(0,0,0)}and(u1,u2,u3)∈K,where

Then there exists 0<µ<1 such that R(u1µ,u2µ,u3µ)=0 and
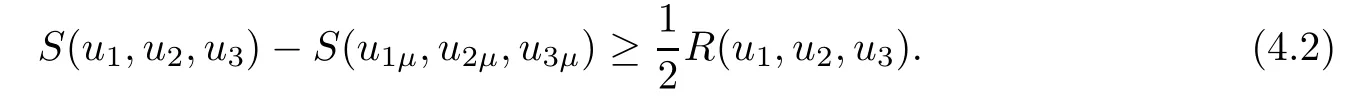
Here,S(u1,u2,u3)and R(u1,u2,u3)are defined by(2.3)and(2.4),respectively.
Proof By a direct calculation,we can easily show estimate(4.2).
Now,we begin to show Theorem 2.2.
Proof of Theorem 2.2 Let(E1,E2,E3)∈H1r(R3)×H1r(R3)×H1r(R3)be a solution to equations(1.1)-(1.3)with(1.4)on[0,T).By the conservation laws of the total mass and of the total energy(2.1)and(2.2),we get
Let

By a direct calculation,one achieves

We further need to show,for some initial data,that the right-hand side of(4.5)is strictly negative(that is,R(E1,E2,E3)<0).One first notices that

Let(E10,E20,E30)∈K such that
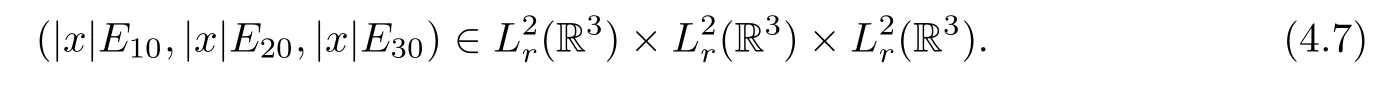
We shall see later that such(E10,E20,E30)exists.We claim that there is a finite time T such that
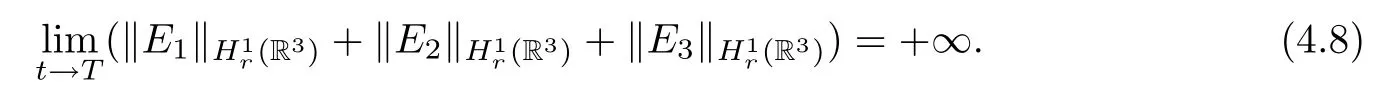
Indeed,for such(E10,E20,E30)∈K,one has
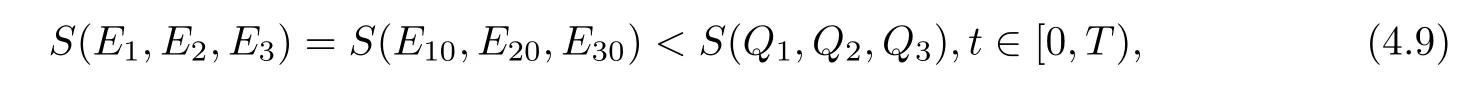
and

The latter is true,for otherwise,by continuity,there would exist a t1>0 such that 0<t1<T,and
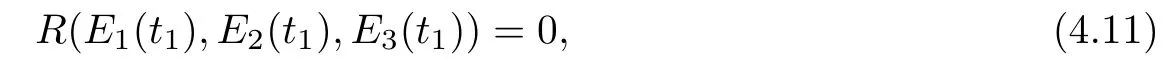
which implies that(E1(t1),E2(t1),E3(t1))∈M.This contradicts Theorem 2.1 and(4.9).
Next,for a fixed t∈[0,T),(E1,E2,E3)=(E1(t),E2(t),E3(t)),and let 0<µ<1 be such that
Proposition 3.3).Since

in view of Proposition 4.1,we have
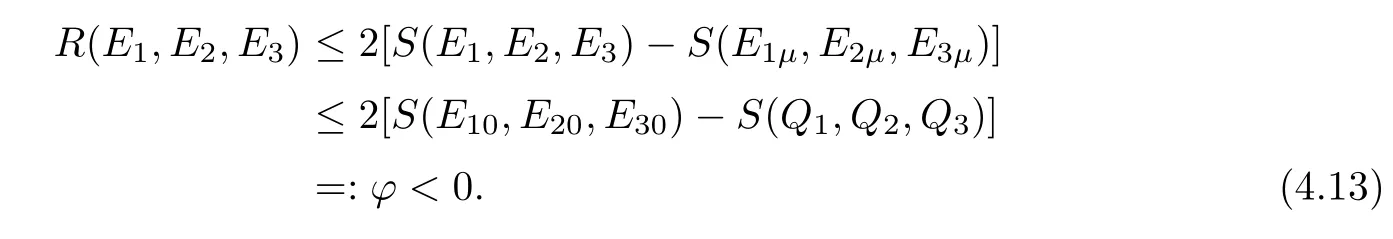
(4.5)and(4.13)then yield that

which implies that T must be finite and that
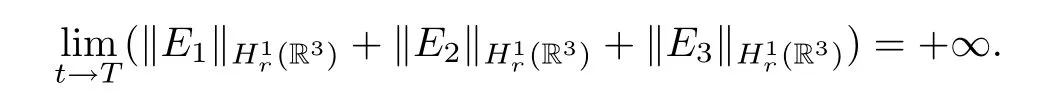
In order to complete the proof of Theorem 2.2,we need to show(E10,E20,E30)∈K with(4.7). Let
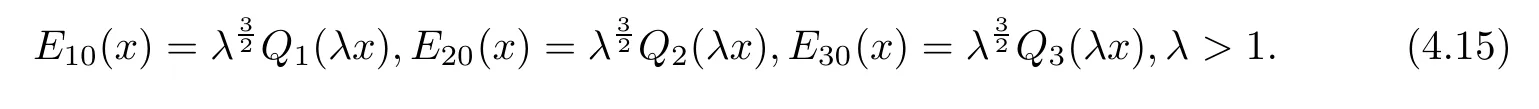
By Proposition 3.3,the functions E10(x),E20(x),E30(x)verify
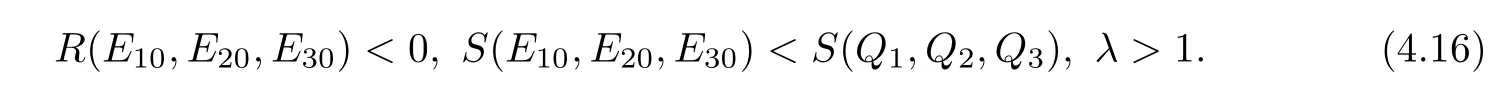
In addition,by Theorem 2.1,one sees that(Q1(x),Q2(x),Q3(x))have exponential decays at infinity,and hence
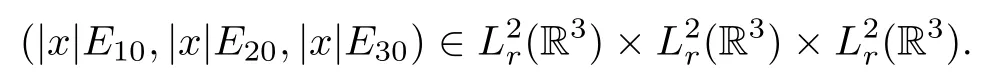
As λ→1,

can be made arbitrarily small.We thus complete the proof of Theorem 2.2.
[1]Berestycki H,Cazenave T.Instabilit´e des´etats stationnaires dans les´equations de Schr¨odinger et de Klein-Gordon non lin´eairees.C R Acad Sci Paris,1981,293:489-492
[2]Berestycki H,Lions P L.Nonlinear scalar field equations,I.Existence of a ground state.Arch Rat Mech Anal,1983,82:313-345
[3]Berestycki H,Lions P L.Nonlinear scalar field equations,II.Existence of infinitely many solutions.Arch Rat Mech Anal,1983,82:347-375
[4]Cazenave T,Lions P L.Orbital stability of standing waves for some nonlinear Schr¨odinger equations. Commun Math Phys,1982,85:549-561
[5]Dai J J,He Q H.Nodal bound states with clustered spikes for nonlinear Schr¨odinger equations.Acta Math Sci,2014,34B(6):1892-1906
[6]Dendy R O.Plasma Dynamics.Oxford:Oxford University Press,1990
[7]Gan Z H,Zhang J.Sharp threshold of global existence and instability of stangding wave for a Davey-Stewartson System.Commun Math Phys,2008,283:93-125
[8]Gan Z H,Zhang J.Blow-up,global existence and standing waves for the magnetic nonlinear Schr¨odinger equations.Dis Cont Dyn Syst,2012,32(3):827-846
[9]Gan Z H,Zhang J.Nonlocal nonlinear Schr¨odinger equations in R3.Arch Rational Mech Anal,2013,209: 1-39
[10]Grillakis M.Linearized instability for nonlinear Schr¨odinger and Klein-Gordon equations.Comm Pure Appl Math,1988,41:747-774
[11]Grillakis M,Shatah J,Strauss W.Stability theory of solitary waves in the presence of symmetry,I*.J Funct Anal,1987,74:160-197
[12]Jiang X,Gan Z H.Collapse for the generalized three-dimensional nonlocal nonlinear Schr¨odinger equations. Adv Nonlinear Stud,2014,14:777-790
[13]Jones C.An instability mechanism for radically symmetric standing waves of a nonlinear Schr¨odinger equation.J Differential Equations,1988,71:34-62
[14]Kono M,Skoric M M,Ter Haar D.Spontaneous excitation of magnetic fields and collapse dynamics in a Langmuir plasma.J Plasma Phys,1981,26:123-146
[15]Laurey C.The Cauchy problem for a generalized Zakharov system.Diff Integral Equ,1995,8(1):105-130[16]Liu Z X.On a class of inhomogeneous energy-critical focusing nonlinear Schr¨odinger equations.Acta Math Sci,2013,33B(6):1522-1530
[17]Miao C X.Harmonic Analysis and Applications to Partial Differential Equations.Monographs on Modern Pure Mathematics No 89.2nd ed.Beijing:Science Press,2004
[18]Miao C X.The Modern Method of Nonlinear Wave Equations.Lectures in Contemporary Mathematics,No 2.Beijing:Science Press,2005
[19]Miao C X,Zhang B.Harmonic Analysis Method of Partial Differential Equations.Monographs on Modern Pure Mathematics,No 117.2nd ed.Beijing:Science Press,2008
[20]Shatah J,Strauss W.Instability of nonlinear bound states.Commun Math Phys,1985,100:173-190
[21]Strauss W A.Existence of solitary waves in high dimensions.Commun Math Phys,1977,55:149-162
[22]Wan L L,Tang C L.Existence of solutions for non-periodic superlinear Schr¨odinger equations without(AR)condition.Acta Math Sci,2012,32B(4):1559-1570
[23]Weinstein M I.Nonlinear Schr¨odinger equations and sharp interpolation estimates.Commun Math Phys,1983,87:567-576
[24]Weinstein M I.Lyapunov stability of ground states of nonlinear dispersive evolution equations.Commun Pure Appl Math,1986,39:51-68
[25]Xu J,Fan E G.A Riemann-Hilbert approach to the initial-boundary problem for derivative nonlinear Schr¨odinger equations.Acta Math Sci,2014,34B(4):973-994
[26]Zhang J.Sharp threshold for blowup and global existence in nonlinear Schr¨odinger equations under a harmonic potentia.Commun PDE,2005,30:1429-1443
[27]Zakharov V E.The collapse of Langmuir waves.Soviet Phys,JETP,1972,35:908-914
[28]Zakharov V E,Musher S L,Rubenchik A M.Hamiltonian approach to the description of nonlinear plasma phenomena.Physics Reports,1985,129(5):285-366
Appendix A
In this Appendix,we will show the exponential decay at infinity of the solution(Q1,Q2,Q3)to equations(3.48)-(3.50).
Consider equations(3.48)-(3.50):

Let
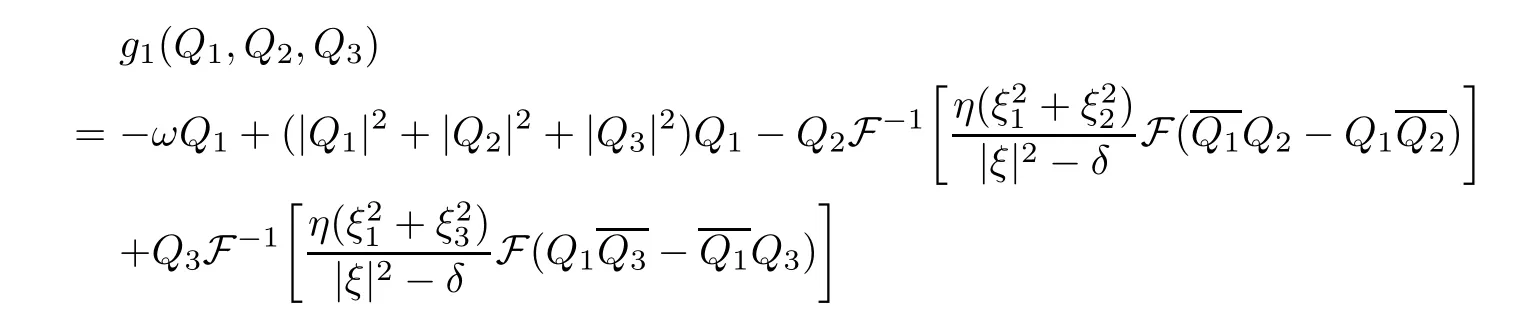
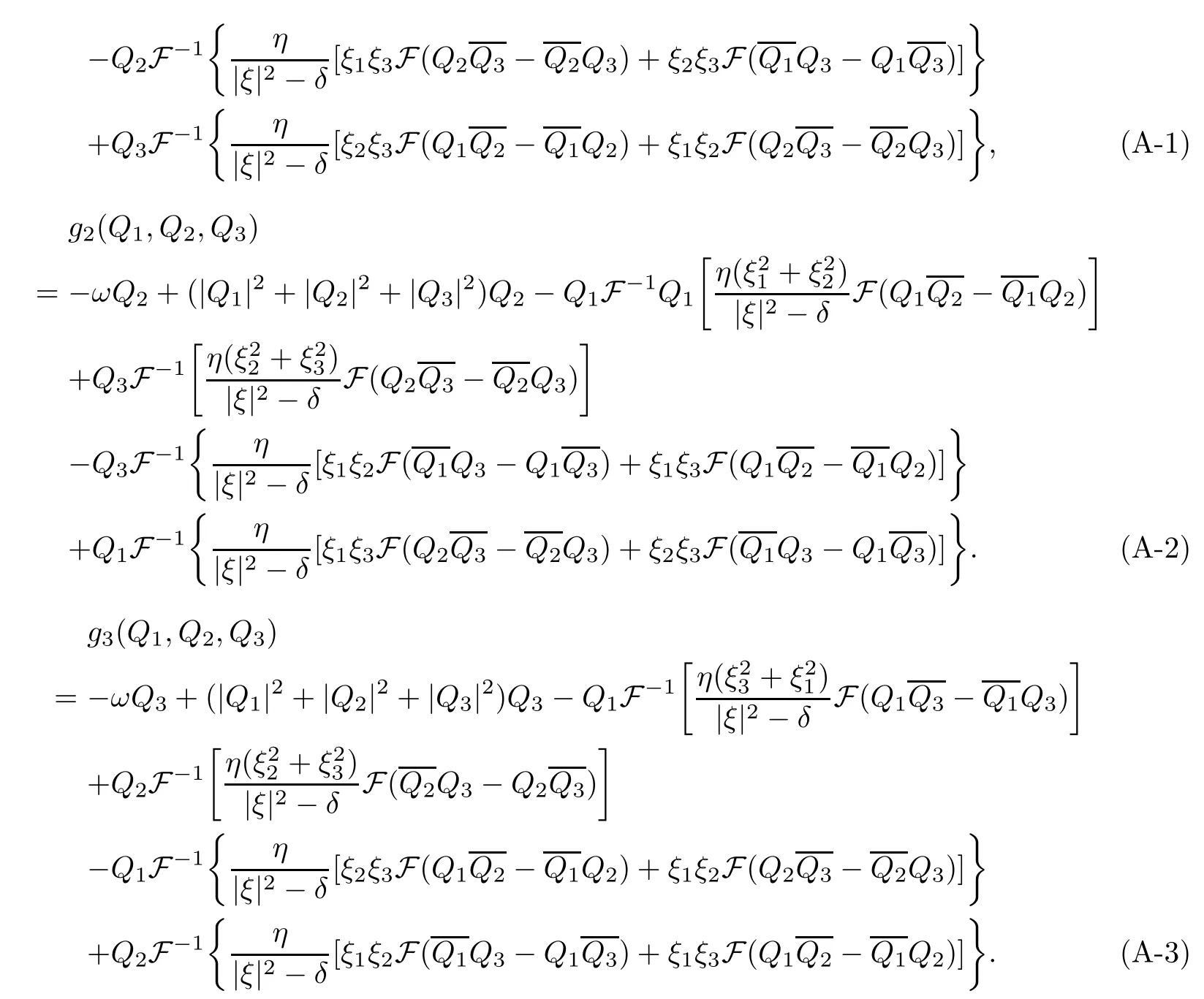
Then equations(3.48)-(3.50)reduce to the following system:
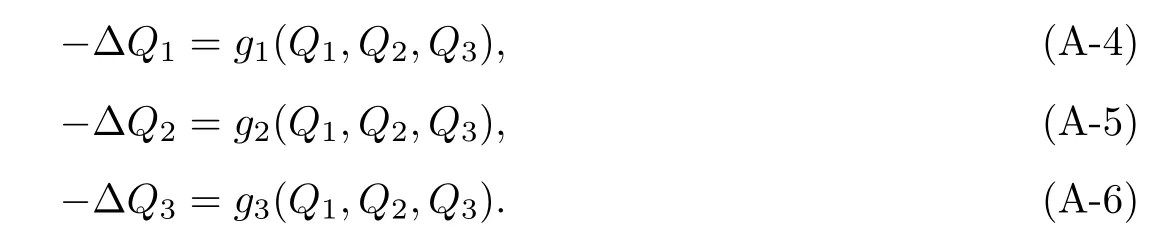
By the expressions of gi(Q1,Q2,Q3)(i=1,2,3),for η>0 and δ≤0,we conclude the following properties:

Furthermore,motivated by Lemma 1 and Radial Lemma A.II in[2,3],we can establish the following two lemmas.
Lemma A1 Under the properties(A-7)-(A-8),if(Q1,Q2,Q3)is a spherically symmetric solution of(A-4)-(A-6)then(Q1,Q2,Q3)∈C2(R3)×C2(R3)×C2(R3).
Lemma A2 Let N=3.The radial function Qi∈H1(R3)(i=1,2,3)is almost everywhere equal to a function Ui(x),continuous for x/=0 and such that

where C3and α3are two constants depend only on the dimension N(N=3).
We now begin to prove the exponential decay at infinity of the solution(Q1,Q2,Q3)to(A-4)-(A-6).That is,we need to show the following proposition.
Proposition A1 Under the properties(A-7)-(A-8),if(Q1,Q2,Q3)is a spherically symmetric solution of(A-4)-(A-6)then
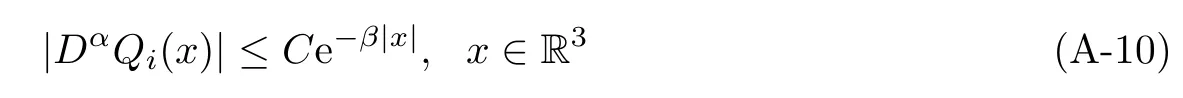
for some C,β>0 and for|α|≤2.
Proof By Lemma A1,Qi(i=1,2,3)is of class C2(R3),and it satisfies the equations below:
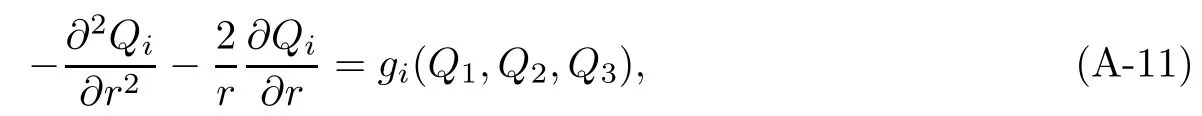
where i=1,2,3.Let Pi=rQi(i=1,2,3),then Pisatisfies
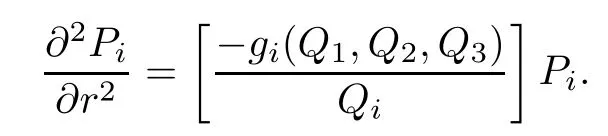
For r large enough,say r≥r0,one gets-gi(Q1,Q2,Q3)/Qi≥ω/ε for any ε≥1.
Indeed,Lemma A2 yields that Qi(r)→0 as r→+∞.
Next,let Wi=P2i(i=1,2,3),then Wisolves
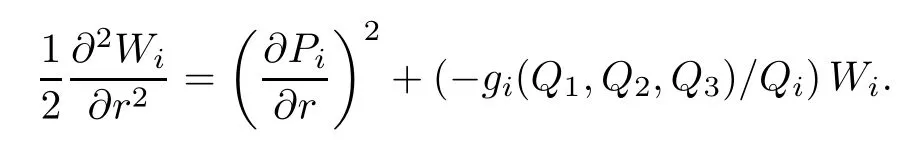
Thus for r≥r0one hasand Wi≥0.
Further,let
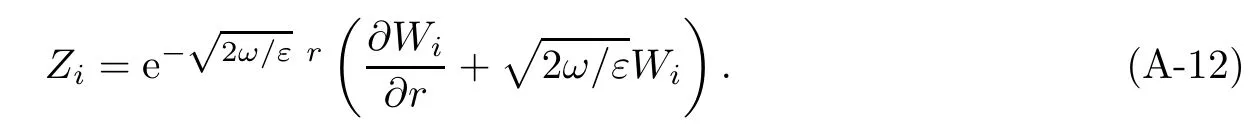
Direct calculation yields that

This implies that Ziis nondecreasing on(r0,+∞).
We now claim that

Otherwise,if there exists r1>r0such that Zi(r1)>0,then Zi(r)≥Zi(r1)>0 for all r≥r1. In view of(A-12),
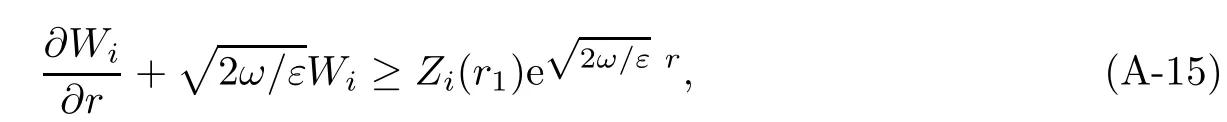
(A-14)then implies that
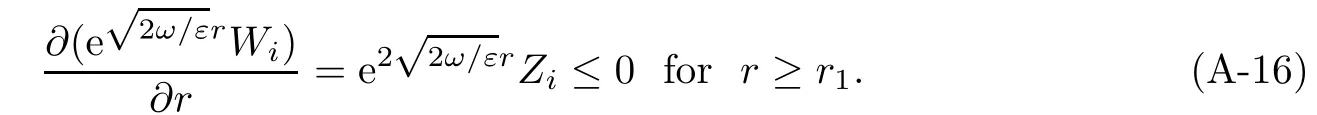
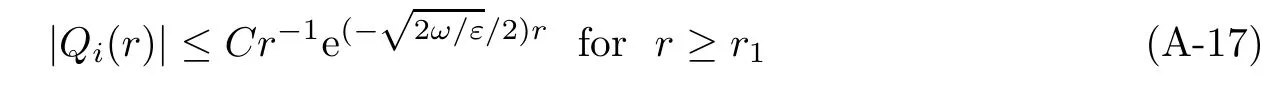
Next,we show the exponential decay of(i=1,2,3)at infinity.
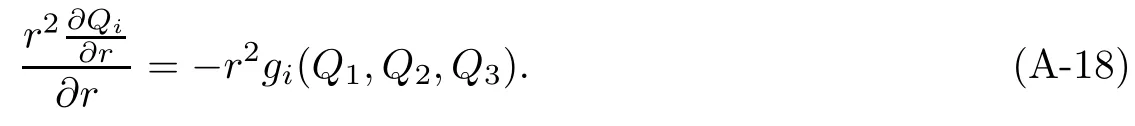
Applying(A-7)and the exponential decay of Qi,it is easily verified that for r large enough,say r≥r0,one has
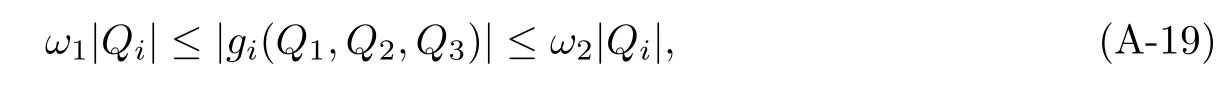
where ω2≥ω1≥0.Hence integrating(A-18)on(r,R),using(A-17)and letting r,R→+∞ shows that r2has a limit as r→+∞.This limit can only be zero by(A-17).
Now,integrating(A-18)on(r,+∞)then yields thathas exponential decay.
Finally,the exponential decay of(and thus|DαQi(x)|for|α|≤2)follows immediately from equations(A-11).
The proof of the exponential decay of Qiat infinity is completed.
∗Received September 29,2013;revised December 26,2014.This paper is supported by National Natural Science Foundation of China(11171241),Program for New Century Excellent Talents in University(NCET-12-1058).
 Acta Mathematica Scientia(English Series)2015年5期
Acta Mathematica Scientia(English Series)2015年5期
- Acta Mathematica Scientia(English Series)的其它文章
- ALL MEROMORPHIC SOLUTIONS OF AN AUXILIARY ORDINARY DIFFERENTIAL EQUATION AND ITS APPLICATIONS∗
- APPROXIMATION OF COMMON FIXED POINT OF FAMILIES OF NONLINEAR MAPPINGS WITH APPLICATIONS∗
- SOME COMPLETELY MONOTONIC FUNCTIONS ASSOCIATED WITH THE q-GAMMA AND THE q-POLYGAMMA FUNCTIONS∗
- SUB-ADDITIVE PRESSURE ON A BOREL SET∗
- AN APPLICABLE APPROXIMATION METHOD AND ITS APPLICATION∗
- EVOLUTION FILTRATION PROBLEMS WITH SEAWATER INTRUSION:TWO-PHASE FLOW DUAL MIXED VARIATIONAL ANALYSIS∗
