NSMD和LMSST相结合的变转速滚动轴承故障诊断方法

尤光辉,吕勇,易灿灿,余肇鸿

(1.武汉科技大学 冶金装备及其控制教育部重点实验室,武汉 430081;2.武汉科技大学 机械传动与制造工程湖北省重点实验室,武汉 430081;3.浙江机电职业技术学院,杭州 310053)

滚动轴承在高速、重载的运行环境下长时间工作,故障率很高[1]。一旦滚动轴承发生故障,会影响设备的正常运行,甚至引发安全事故,造成严重的人员伤亡。因此,实现对滚动轴承运行状态的监测和故障诊断具有十分重大的工程意义[2]。

振动信号能够直接地反映机械设备各个零部件的实际运行状态,因此对振动信号的分析是实现故障诊断的重要手段,然而工业现场滚动轴承采集到的振动信号往往包含大量的噪声,这对分析结果的准确性有着很大的影响,为了在含噪信号中准确地提取特征组分,就需要对信号进行降噪处理,而传统的降噪算法如小波阈值去噪[3]、滤波去噪[4]等往往容易丢失有效特征,导致诊断效果不佳。局部均值分解(Local mean decomposition, LMD)[5]将信号分解为乘积函数之和,通过选取与原始信号相关性最大的分量以实现去噪,但由于LMD存在着模态混合的缺点,使得分解结果产生偏差[6]。变分模态分解(Variational mode decompositon, VMD)[7]将信号分解为若干个相同中心频率的模态分量,然而VMD的实际效果受到分解层数K和二次惩罚因子等参数[8]的制约。针对上述问题,本文提出非线性稀疏模式分解(Nonlinear sparse mode decomposition, NSMD)算法,利用奇异局部线性算子对局部窄带分量进行检测提取,分解结果的特征更加接近于原始信号,具有良好的鲁棒性和自适应性[9]。

对于变转速工况下振动信号的故障诊断,时频分析(Time-frequency analysis,TFA)是一种有力的工具,通过对去噪后的信号采用时频域联合分布来表征信号的瞬态特性[10]。短时傅里叶变换(Short-time fourier transform, STFT)[11]和连续小波变换(Continuous wavelet transform,CWT)[12]等经典时频变换算法通过对信号局部加窗,在窗口内进行时频转换,将得到的瞬态拼接形成连续的时频分布,但其计算结果在时频面上的能量不够集中。Daubechies等[13]提出的同步压缩变换(Synchrosqueezing transform, SST)在STFT或CWT的基础上进行瞬时频率(Instantaneous frequency, IF)估计,沿着频率方向对时频面能量进行重新分配,使时频脊线能量围绕着瞬时频率曲线进一步集中,但SST的结果仍存在着时频能量局部发散的问题。针对SST算法的改进研究中,典型的是沿着高阶方向提出的2阶同步压缩变换(Second-order synchrosqueezing transform, SST2)[14],使用泰勒展开式对IF进行2阶估计,在调频信号的应用中有着较好的效果,但其鲁棒性不佳。此外,还有学者从多次压缩的角度出发提出多重同步压缩变换(Multiple synchrosqueezing transform, MSST)[15],对SST进行多次压缩以达到集中脊线能量的目的,但其造成了算法冗杂,运算速度慢。在对SST的局部细节处理方面,局部最大值同步压缩变换(Local maximum synchrosqueezing transform, LMSST)[16]相比于上述方法,能够有效提高时频面的细节刻画,脊线清晰能量集中,且不具有算法繁琐性,有着较好的应用潜力。

因此,本文提出一种变转速滚动轴承故障诊断方法,首先利用NSMD对变转速振动信号进行分解,利用分解分量的频谱最大相关性进行最佳分量的选择,去除噪声等其他无关分量的影响,然后对选取的最佳分量利用LMSST获得能量集中的高分辨率时频表达,最后进行时频脊线的提取,并将其与理论故障特征频率曲线进行比较,以实现变转速下滚动轴承的故障诊断。本文进行了数值模拟仿真与变转速试验台数据分析,验证了该方法的有效性。

1 理论描述

1.1 非线性稀疏模态分解

对于一个输入信号s(t),将其分解为期望模式vi(t)和剩余信号u(t),则其表达式写为

(1)

式中k为多分量信号的个数。

假设T为一个局部奇异线性算子,则对于时间t,T可以表示为:T(v(t))=0。信号vi(t)在算子T的零空间中,也即信号vi(t)被T映射到零空间。u(t)可以表示为原始信号s(t)经过T映射后的残差分量,即T(s(t))=u(t),则u(t)可以进一步表达为

u(t)=min[‖T(s(t)-u(t))‖2+λ‖L(u(t))‖2]

(2)

式中:L(u(t))为u(t)的主对角矩阵;λ为拉格朗日系数。

而在算法的应用中,如果T是微分算子,一次迭代中不能够完全提取出vi(t),因此引入泄漏因子γ进行求解,则式(2)改写为

u(t)=min[‖T(s(t)-u(t))‖2+λ1‖L(u(t))‖2+

γ‖s(t)-u(t)‖2+F(T)]

(3)

式中:λ1为拉格朗日系数;最后一项F(T)用于对算子T中的参数进行规范化。

为了求解上述方程,选择以下微分算子

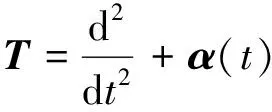
(4)

λ1(‖L(u)‖2+γ‖s-u‖2)+λ2‖L(α)‖2]

(5)

但是式(4)的微分算子并不适用于某些特殊的信号模型,只对调频信号有明显的作用。因此根据质量弹性阻力振动,采用2阶微分算子

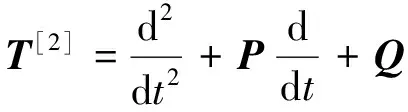
(6)

假设分解分量为A(t)·cos(ω(t)t+b),则有

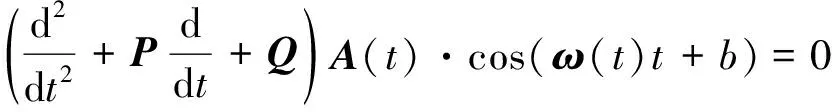
(7)

令φ(t)=ω(t)t+b,则由式(7)可以得到:

(8)

通过求解以上方程,可以得到:

(9)

则式(6)的微分算子可以写成

进一步地,有:

T[2]=D2+PD+Q

λ2(‖D2Q‖2+‖P‖2)]

(11)

式中:D和D2分别为1阶和2阶微分算子;γ通常是一个非常小的数字,设γ=0.001;λ1和λ2通常设为0.1和1。上式的迭代终止条件设置为‖u(t+1)-u(t)‖<ε‖s(t)‖,其中ε=0.000 1。

通过将式(11)最小化即可得到第一个分解非线性稀疏分量,通过重复上述步骤得到后续的分解分量,从而实现将信号分解为多个非线性稀疏分量的和。

1.2 局部最大值同步压缩变换

对于NSMD分解的结果vi(t),(i=1,2,…,k)通过计算每个分量的频谱,将频谱与原始信号s(t)的频谱进行比对,保留一个或多个相关度最大的分量为最佳分量,进行进一步的分析,假设得到的分量为f(t),其STFT写为

(12)

其中,为定义在Schwartz空间中的窗函数,对STFT的结果G(t,ω)进行瞬时频率估计,则

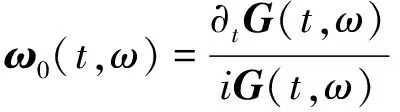
(13)

基于STFT的SST为

(14)

由式(14)可知,SST在STFT的基础上使用同步压缩算子,将时频面的能量往估计的IF曲线上压缩,为了获得能量更加集中的时频表达。通过检测STFT时频谱在频率方向上的局部最大值,构建了一种新的频率重分配算子,将所有被压缩的能量沿频率方向重新分配到估计的IF轨迹中,则

ωm(t,ω)=

(15)

(16)

根据以上分析,基于STFT的LMSST表示为

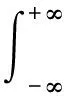
(17)

1.3 NSMD和LMSST相结合的变转速滚动轴承故障诊断方法

本文结合NSMD和LMSST各自的优点,NSMD在分解信号时具有更好的鲁棒性和自适应性,适用于将含噪数据中的有效分量、噪声分量等各组分进行分解,选择其中包含故障特征的有效分量,舍弃噪声分量,以此达到数据降噪的作用。针对转速变化工况下的故障诊断,LMSST对时频脊线有着更强的刻画能力,因此在对数据进行降噪预处理后,利用LMSST对时频平面局部细节进行描述,从而获得清晰、能量集中的故障特征频率脊线。

本文提出方法的流程具体步骤为:

1)对于采集的振动信号数据,利用NSMD对变转速振动信号进行分解,获得若干分量,对分解结果的每个分量,利用快速傅里叶变换(Fast fourier transform,FFT)[17]得到每个分量的频谱,通过将分量频谱与原始的频谱进行比对,保留一个或多个相关度最大的分量为最佳分量,去除噪声等其他无关分量,选择有效分量进行后续的分析;

2)对选取的最佳分量利用LMSST获得时频平面能量集中的时频表达;

3)提取LMSST时频谱中的脊线,将其与不同类型故障的理论特征频率曲线进行比较,从而实现变转速下滚动轴承的故障诊断。

本文提出方法的流程图如图1所示。

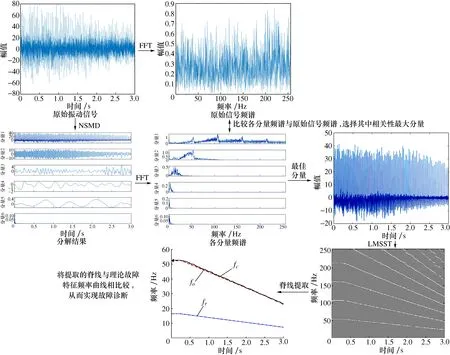
图1 本文提出方法的流程图

2 数值模拟仿真

为验证本文提出方法的有效性,设计信号进行模拟仿真,定义仿真信号s(t)为:

(18)

式中:s1(t)和s2(t)分别为线性分量和调频分量;n(t)为添加的噪声,设置信噪比SNR=-5 dB。图2所示为仿真信号的时域图及频谱,图3为仿真信号的理想IF曲线。

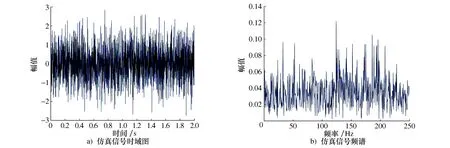
图2 仿真信号时域图及频谱

图3 仿真信号理想IF曲线

由于噪声的干扰,图2b)中的频谱结构十分杂乱,无法对定义信号所在频带进行判断,因此需要利用信号分解算法进行去噪处理,将信号中不同的模式分量进行分解,根据分解结果的频谱特征,从而选择最佳的单个或多个分量。

图4所示为利用LMD、VMD和NSMD这3种分解算法对仿真信号的分解结果及其频谱。从图4分解结果可以看出,在LMD和VMD的分解结果频谱中无法观察到时变特征。而在图4f)所示NSMD的分解结果频谱中,分量1中可以看到在130～200 Hz范围内存在调制现象,对应为信号分量s2(t),而分量2在130～200 Hz范围内有较高能量,对应为信号分量s1(t),因此在3种分解算法中,NSMD具有最佳的效果。

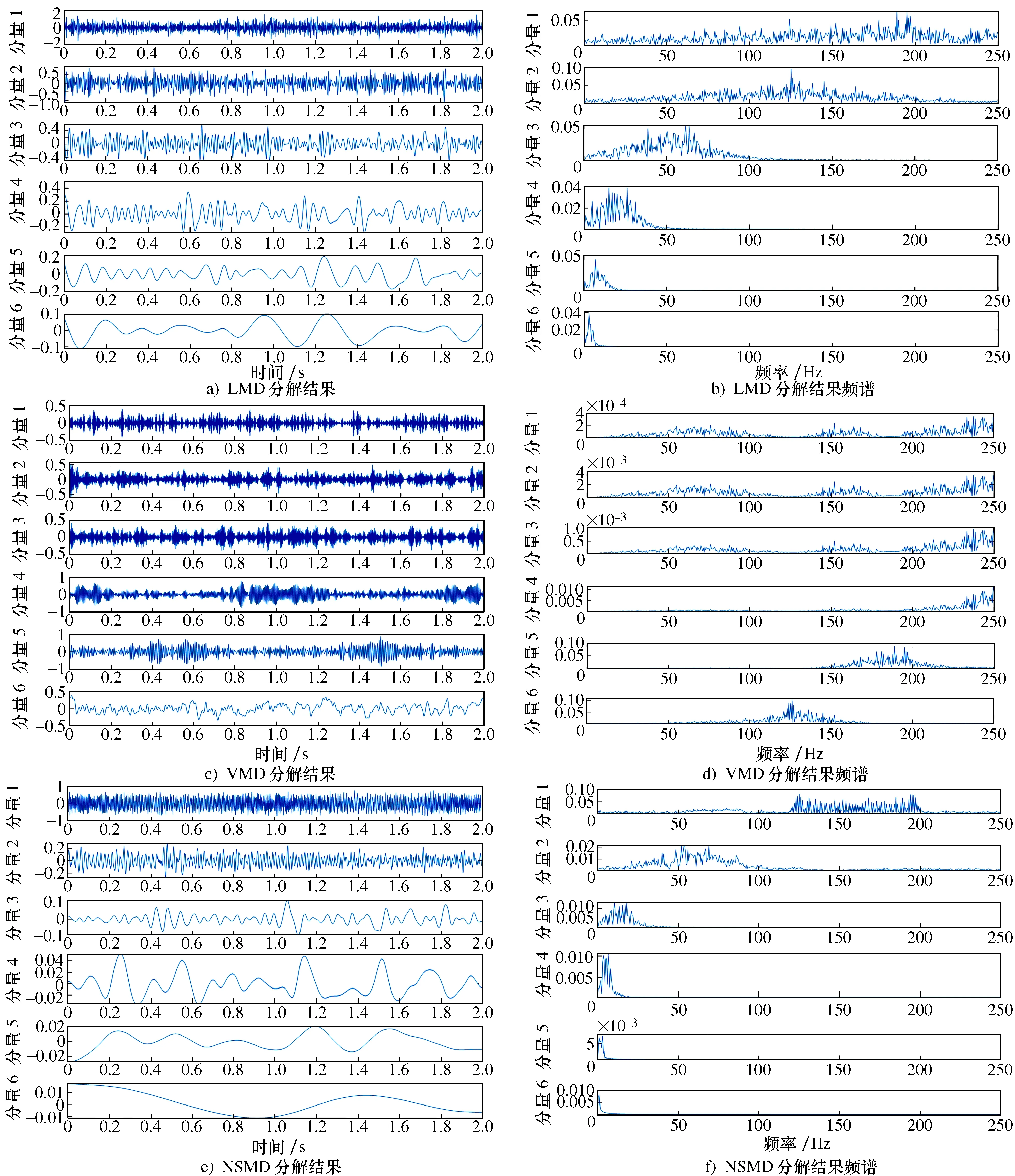
图4 LMD、VMD和NSMD这3种算法对仿真信号的分解结果及其频谱

对应时变信号,仅仅依靠传统频谱无法对信号的时变特征进行表征,因此将NSMD分解的分量1和分量2相加作为最佳分量进行时频分析,分别使用SST、MSST、SST2、LMSST进行处理,得到的结果如图5所示。由图5可知:SST、MSST、SST2方法均存在不同程度的时频能量发散,而LMSST的处理结果中的时频脊线清晰,能量聚集性最好。通常Renyi熵是被用于表征时频分析结果好坏的指标,Renyi熵值越低表示时频能量聚集性越好[18],表1所示为SST、MSST、SST2、LMSST这4种时频分析方法的Renyi熵值。

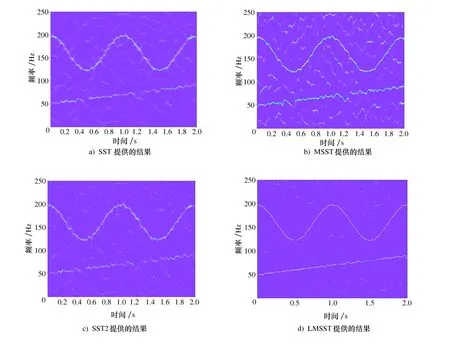
图5 4种时频分析算法的结果

表1 仿真模拟信号不同分析方法得到的Renyi熵值比较

由表1可知:LMSST分析结果具有最小的Renyi熵值,表明其具有最佳的时频分析效果。通过以上分析,可以得出NSMD相比于其他分解算法,对信号的分解具有最好的效果,LMSST相比于其他时频分析算法,对分解后的信号具有最好的时频刻画能力。

3 实验数据分析

为进一步验证本文所提出方法的有效性,利用试验台数据进行测试,如图6所示为试验台实物图及结构简图。

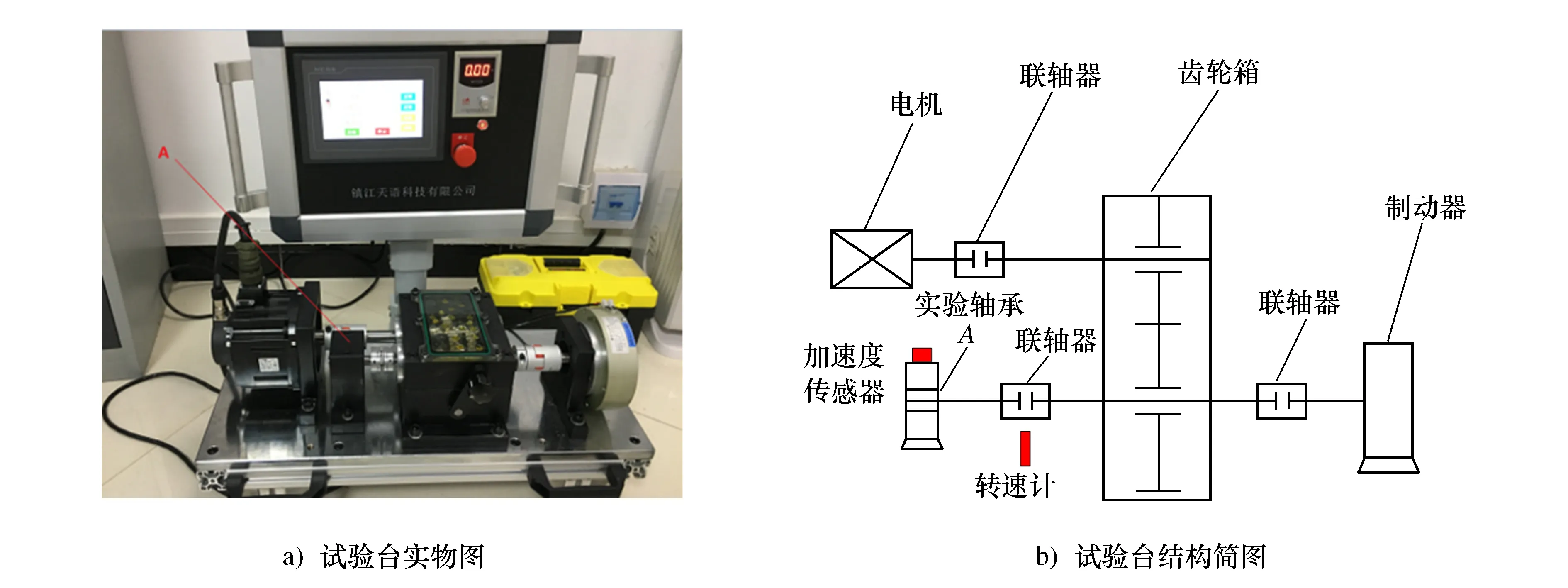
图6 试验台实物图及结构简图

实验轴承故障类型为外圈故障,实验变转速工况为电机转速从1 650 r/min开始减速到0的过程,将磁吸式加速度传感器放置于轴承端盖上进行振动信号采集,将转速传感器对准与实验轴承相连的联轴器进行转速测量。此外,试验台齿轮箱的减速比为5∶3,实验采样频率为1 280 Hz,实验采集振动数据的时长为3 s。滚动轴承型号为6 202,其滚动体个数z=8。采集原始振动信号的时域图及频谱如图7所示。

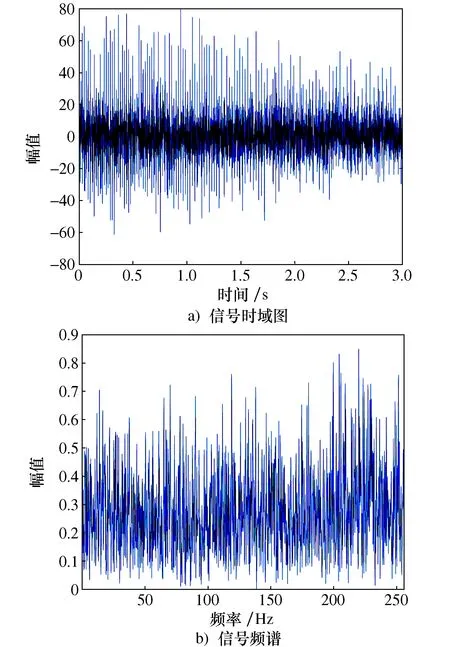
图7 振动信号时域图及频谱

由于包含有较多噪声,为了使信号时频分析更加准确,首先利用NSMD对实测振动信号进行分解,降低噪声等无关因素的影响。NSMD分解结果及各个分量的频谱如图8所示。分量1的频谱中在0～50 Hz、50～100 Hz、100～150 Hz呈现出一定的规律,可以大概确定故障特征频率在0～50 Hz之间,其2倍频及3倍频则位于50～100 Hz、100～150 Hz之间。因此,选择NSMD分解的分量1作为最佳分量,并利用LMSST进行后续的时频分析。

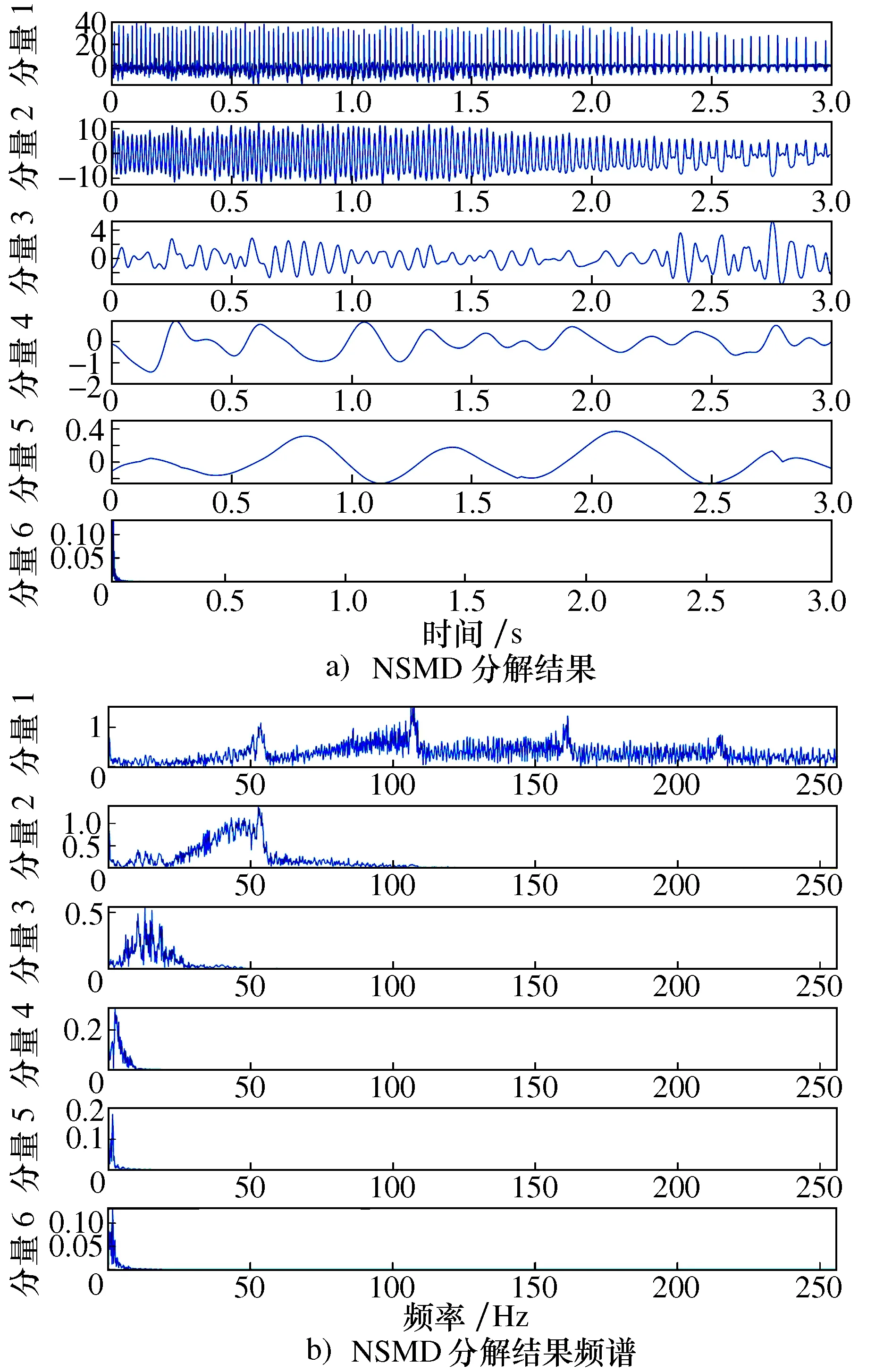
图8 NSMD对实测振动信号的分解结果及频谱

利用SST、MSST、SST2和LMSST这4种方法对选择NSMD分解的分量1进行分析,计算结果如图9所示,可以看出其他方法所得到的局部效果均不佳,只有LMSST获得的时频图中能够很好地识别出故障特征频率曲线fc、2倍频2fc及其3倍频3fc等,无局部能量发散,脊线光滑且能量集中。进一步用定量指标Renyi熵来比较不同时频分析方法的效果,其结果如表2所示,LMSST方法的Renyi熵数值最低,表明其具有最佳的分析效果。

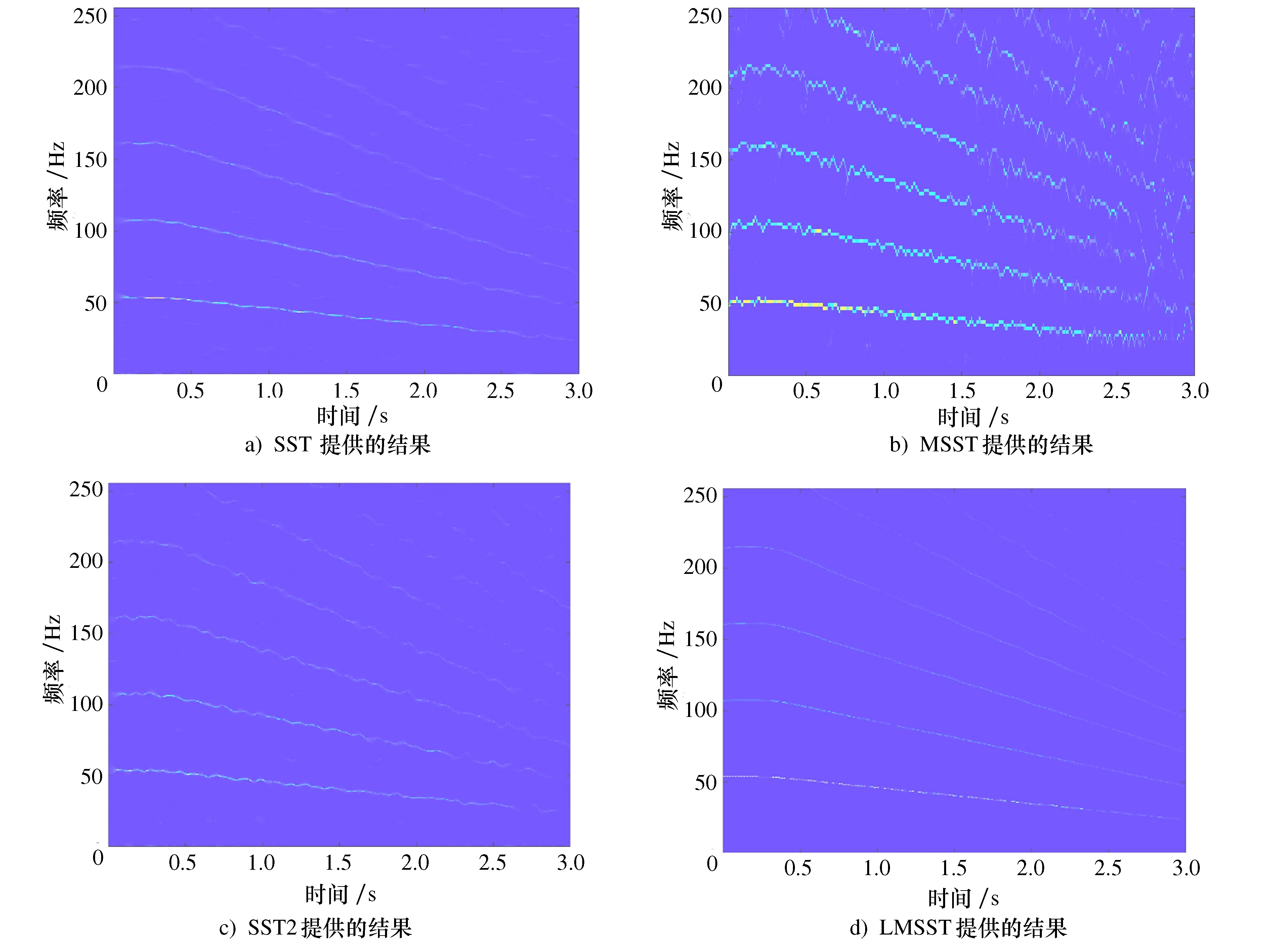
图9 4种时频分析算法对分量1的计算结果

表2 实际信号不同分析方法得到的Renyi熵值比较

对图9d)的脊线进行提取,得到的结果如图10所示。

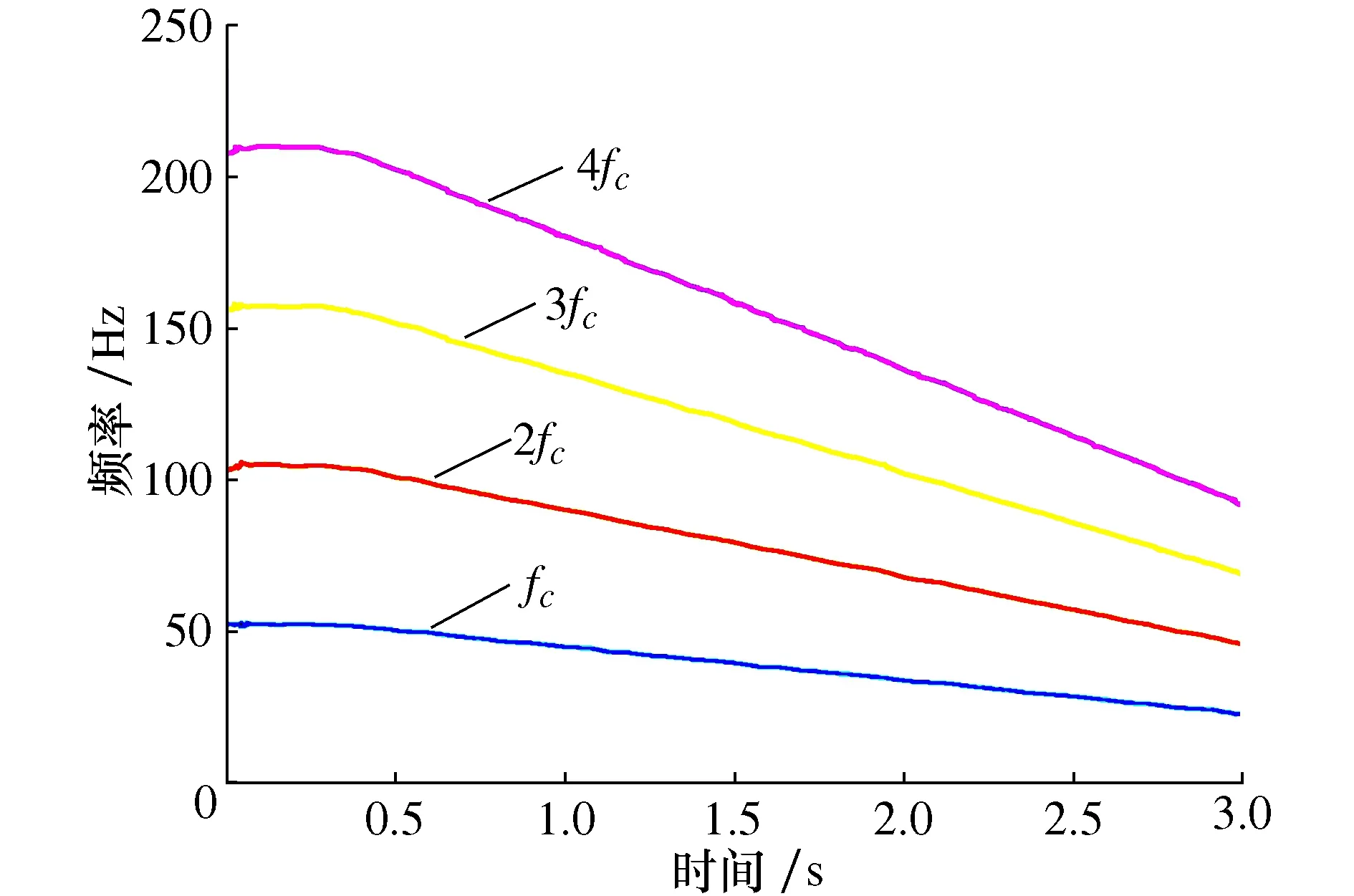
图10 LMSST结果脊线提取

根据转速计测得的转速可以计算得到转频fr,根据经验公式fo=0.4zfr,可以得到滚动轴承的理论外圈故障特征频率fo,将转频fr、LMSST计算的故障特征频率fc与理论外圈故障特征频率fo的曲线绘制在同一张图上,如图11所示,发现fc与fo曲线十分吻合,因此判断实验滚动轴承为外圈故障,这与实验预设故障类型一致。

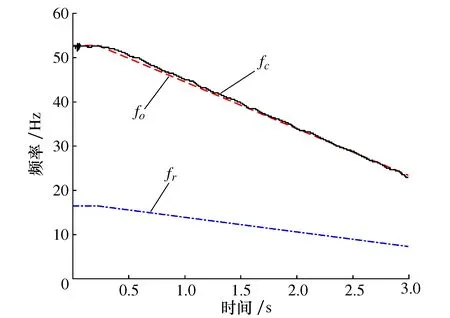
图11 计算故障特征频率与理论值比较

4 结论

本文提出了NSMD和LMSST相结合的变转速工况下滚动轴承故障诊断方法,通过对振动信号进行NSMD分解,去除噪声、结构共振等无关分量,选择最佳分量,在此基础上利用LMSST获得能量集中的时频表达,提取时频谱中的脊线,并将其与理论故障特征频率曲线相比较,从而实现滚动轴承的故障诊断。通过数值仿真分析并对试验台滚动轴承进行故障诊断,验证了方法的可行性。由于本文的研究仅仅针对转速变化工况下的振动信号,没有考虑变载荷等复杂工况,后续将针对多种复杂工况下的振动信号降噪、特征提取等方面展开研究。