基于相位法的密集小波公共脊线提取方法

蒋永华，莫晓强，尤佳伊，沈梦杰，沈凤良

（浙江师范大学精密机械研究所，浙江金华 321004）

基于相位法的密集小波公共脊线提取方法

蒋永华，莫晓强，尤佳伊，沈梦杰，沈凤良

（浙江师范大学精密机械研究所，浙江金华 321004）

针对传统小波脊线提取方法对密集脊线的提取存在着分辨率不足等缺点，提出一种基于相位法的密集小波公共脊线提取方法。通过分析密集单频叠加信号和密集调频叠加信号的小波公共脊线的相位特点，利用小波脊线的相位法来提取信号的公共脊线。仿真算例结果表明：该方法能有效地提取出密集小波公共脊线，且方法简单、准确，具有较快的收敛性。将其应用于实际齿轮箱故障分析中，能有效地提取故障特征，诊断出齿轮箱故障。

小波脊线；相位法；密集脊线；小波变换

0 引言

在机械故障诊断中，常常利用小波脊线来提取信号的故障特征[1-3]。小波脊线包含了信号的全部或大部分信息，可以通过小波变换域中对应脊线上的信息来表达，并且可以通过脊线重建原信号；因此，小波脊线也被广泛用于信号的去噪和压缩[4-5]。

单一信号分量在小波变换域上呈现出一条对应的脊线，当信号含有两个或者两个以上分量时，则会在变换域上出现相应的多条脊线。如果两条脊线互相靠近到一定程度时，则会出现相互干扰的现象，表现为两条脊线之间的中间部位出现一些虚假分量，其幅度可能接近甚至超过真实脊线的幅度，并且脊线上的分布会因为扰动而出现周期性的波动，从而影响到脊线的正确识别与提取。

DELPRAT等[6]建立了小波脊线提取的迭代算法。张晓冬等[7]提出了一种基于重定位方法的密集脊线提取方法，但是重定位提取密集公共脊线的方法比较复杂。本文通过研究密集单频叠加信号和密集调频叠加信号的小波公共脊线的相位规律，提出利用小波脊线的相位法来提取信号的公共脊线。

1 小波脊线

任意的实信号x（t）∈L2（R）均可表示为

x（t）=A（t）cos（φ（t））（1）

式中：A（t）≥0——瞬时幅值；

φ（t）∈[0，2π）——瞬时相位。

x（t）的解析信号[8]可表示为

式中：H——信号的Hilbert变换。

令小波函数为ψ（t）＝Aψ（t）exp[jφψ（t）]，则信号s（t）的小波变换为

此处用符号ar（b）表示小波脊线，ar（b）是平移参数b的函数。小波脊线上的点（ar（b），b）称为小波脊点。

小波曲线是在相平面上通过点（ar（b0），b0），且满足ts（a，b）=b0的所有点（a，b）的集合，即

对于给定小波曲线，即在驻点ts（a，b）=b0处，小波曲线与小波脊线的交点处，小波变换的相位φ（a，b）有如下特性[10-12]：

φ′ψ（0）为小波函数的中心频率，式（8）说明，沿着一给定小波曲线，小波变换的相角相对平移量b的偏导数在与小波脊线的交点处的值等于伸缩小波的中心频率[2]。

2 密集脊线提取中的分辨率不足问题设信号的形式为

其中w1和w2为常数。设w1≥w2且w2=kw1（k≥1）

选择Morlet小波为分析小波

小波参数β和w0根据信号分量频率w1和w2的具体数值选择，使得在分布图中脊线所在的位置适中。这两个数值在确定后即为常数。

根据连续小波变换的公式可得到信号对应的连续小波变换为

根据变换域上脊线的定义可知，该信号中两个信号分量所对应的脊所在的位置分别为a1=w0/w1，a2=w0/w2。

考虑叠加信号分布在脊a1=w0/w1所在位置上的参数得到

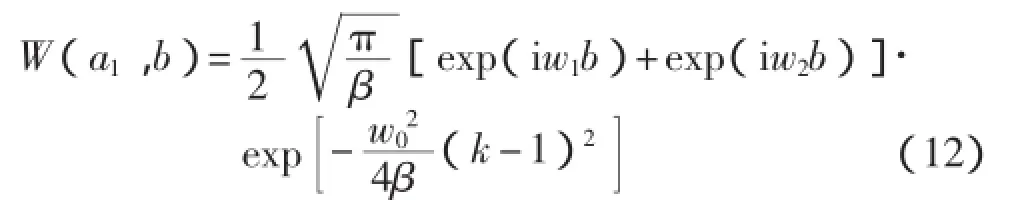
由式（12）可看出，脊线由两部分组成，一部分是频率为w1的单频分量对应的脊线，这部分数据完全反映了该单频分量的波形；另一部分是第2个单频信号所产生的影响，这部分的幅度与选用的小波和两个单频分量的频率比值k有关。

由式（10）～式（12）可看出，在该条脊线上分布的数据呈现出周期波动的形式，并且脊线上数据模值产生的峰点与谷点幅度的大小与两个信号频率的比值之间的关系可表示为

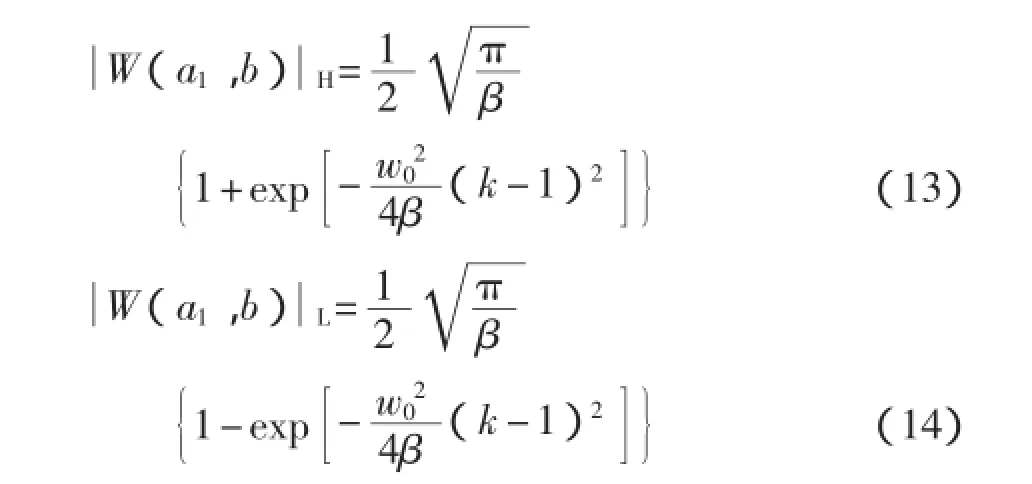
同理，可得到对应着的另一个信号分量及所在位置a2=w0/w2上的分布。在这条脊上分布的数据同样呈现出周期波动的形式，并且脊线上数据的模值产生的峰点与谷点幅度大小和两个信号频率的比值之间的关系可表示为

在两个信号分量所对应的脊线中间地带，还有另一条脊线

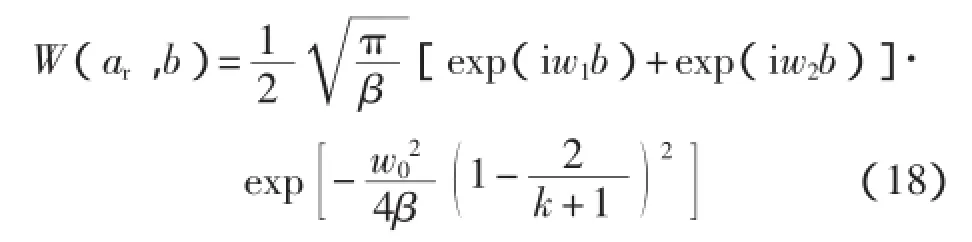
同样考察这条脊上峰点的模值与两个信号频率的比值之间的关系，得到

在谷点的模值为零。

由式（18）知，当两个信号分量的频率比值k较大，即信号分量的频率间隔较大时，在特殊的脊ar上的分布变得很小，此时在a1和a2上的分布较突出，可以区分出两条明显的脊线；当两个信号分量的频率比值减小，即信号分量的频率间隔较小时，两条脊线的距离很近，互相形成干扰，此时在脊ar上的分布很大，与脊a1和a2上起伏波动的分布综合在一起，使得利用提取算法提取出的脊交织在一起。

当脊ar上的模极大值为脊a1和a2上模极大值的一半时，两条对应信号分量的脊线可以区分开来；当k≥2时，在信号分量各自对应的脊线上，所受的另一条脊线的影响随k的增加而趋于不明显，脊线本身的特点更加突出。当1＜k≤2时，在信号分量对应的脊线上，因为其他信号分量的干扰而形成周期性的波动。在扰动最强烈的位置上，干扰项本身形成的波动，其幅值就有可能超过脊上数据的幅值，从而影响到脊线的正确识别与提取。

令s（t）=exp（i2π·20t）+exp（i2π·k·20t）为两个单频信号的叠加，图1所示为k=1.5时两个单频信号所形成的脊的分布情况。

令f（t）=exp（i2π·10t2）+exp（i2π·k·10t2）为两个调频信号的叠加，图2所示为k=2时信号f（t）的脊线幅值三维分布图，图3为k=1.5时信号f（t）的脊线幅值三维分布图。

图1 k=1.5时b取不同值脊线上峰点的模值比较

图2 k=2时f（t）的幅值三维分布图

3 基于相位法的密集公共脊线提取

针对以上问题，本文提出一种基于相位法的密集小波公共脊线提取方法。

图3 k=1.5时f（t）的幅值三维分布图

考虑两个单频信号的情况，令信号

从式（22）可看出，对于两个单频信号的组合来说，脊线上的数据与原信号的波形之间只相差一个恒定的乘积因子c，因此如果用ar来作为公共脊线，可以完全表示两个信号分量所含的全部信息。

影响脊线上分布参数幅值的因子c在两个信号分量的瞬时频率相差较大，即k较大时非常小，但在此情况下，两个信号分量对应的脊线能够很明显地区分开来，不需要定位一条公共脊线。在两个信号分量的瞬时频率逐渐靠近，两条脊线互相影响，出现复杂的脊线分布，即k较小的时候，该因子c取得较大值。此时，虽然根据传统的脊线提取算法所提取的脊线结果交汇在一起，但只要能够确定这条脊线的位置，就能够利用这条脊线上的信息来完全表示和重建。

由式（22）可得出ar上的相位为

对比式（8）与式（24）可知，公共脊线ar可以用改进后的DELPRAT迭代法较精确地提取，从而确定干

则沿着脊线ar，对相位求偏导有扰最大的公共脊线：对于采样周期Ts=1/fs的离散序列s（tk），k=0，1，…，N-1，tk=t0+kTs，令它在给定尺度a下的小波变换Ws（a，tk），其相位为φ（a，k），并定义Db为关于平移参数的离散微分算子。设a0（tk）是ar（tk）的初始估计值，则通过下面的迭代方法计算出小波脊线：

根据所要求的精度，给定一个正数（阈值ε），当满足时，就可以认为ai为最终收敛值，即ar=ai。

4 仿真验证

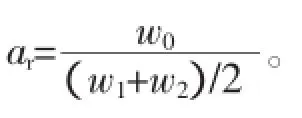
图4 k=1.5时利用相位法提取得到的s（t）的公共脊

图5 k=1.5时利用相位法提取得到的f（t）的公共脊线

图6 单级齿轮箱振动加速度信号

图7 本文方法提取齿轮箱信号小波脊线结果

5 实际应用

齿面损伤是常见的齿轮故障，在时域中局部损伤的振动信号是典型的以齿轮轴的旋转频率为周期的冲击脉冲信号。在重庆大学机械传动国家重点实验室对一具有剥落故障的单级齿轮箱进行实验，采集到的振动加速度信号如图6所示。采样频率为2048Hz，主动轮和从动轮齿数分别为34和65，输入轴转频fr=10.3Hz。利用本文方法对信号进行分析，所得结果如图7所示。

从图7可看到有周期冲击振动，其时间间隔约为0.097 s，即冲击振动的频率约为10.3Hz，与输入轴转频一致，这说明主动轮出现了局部故障。开箱检修发现主动轮发生了严重的剥落，诊断结果与事实相符。

6 结束语

（1）分析了传统方法提取密集脊线存在的分辨率不足的问题。当两个信号的频率之比小于2时，两条脊线之间会出现严重的干扰项，此干扰项会影响到脊线的有效识别和正确提取。

（2）分析了单频、调频叠加信号的公共脊线的表达式，研究其相位特点，提出了基于相位法的密集小波公共脊线提取方法，此方法相比重定位法更加简单快捷。

（3）通过对单频信号和调频信号的仿真算例，证明了该方法的有效性，并将其应用于实际齿轮箱的故障诊断中。

[1]朱洪俊，王忠，秦树人.小波变换对瞬态信号特征信息的精确提取[J].机械工程学报，2005，41（12）：196-199.

[2]秦毅，秦树人，毛永芳.基于小波脊线的解调方法及其在旋转机械故障诊断中的应用[J].机械工程学报，2009，45（2）：231-237.

[3]江涌涛，张春良，胡耀斌，等.小波变换在切削颠振特征提取中的应用[J].中国测试技术，2006，32（3）：7-8，15.

[4]Donoho D L.Denoising by soft thresholding[J].IEEE Transaction on Information Theory，1995，411（3）：610-620.

[5]徐学勇，程康.爆破震动信号模极大值小波消噪方法的改进[J].爆炸与冲击，2009，29（2）：194-198.

[6]Delprat N P，Escudie B，Guillemain P，etal.Asymptotic wavelet and gabor analysis：extraction of instantaneous frequencies[J].IEEE Transactions on Information Theory，1992，38（2）：644-664.

[7]张晓冬.基于脊提取的信号表示和重建[D].南京：东南大学，2003.

[8]Özkurt N，Savac F A.Determination of wavelet ridges of nonstationary signals by singular value decomposition[J]. IEEE Transaction on Circuits and Systems-II：Express Briefs，2005，52（8）：480-485.

[9]蒋永华，汤宝平，邓蕾.基于最优重分配小波尺度谱的小波脊线提取方法[J].振动、测试与诊断，2012，32（1）：62-67.

[10]张征平，陈艳峰.小波分析在高压电机故障检测中的应用[M].北京：中国电力出版社，2009.

[11]陈建文.基于小波脊的数字信号的调制识别[D].郑州：解放军信息工程大学，2007.

[12]魏云冰，王万良，赵燕伟，等.基于小波脊线的刮水器电动机机械特性测试[J].机械工程学报，2006，42（6）：142-144.

Closely wavelet common ridge extraction method based on phase extraction

JIANG Yong-hua，MO Xiao-qiang，YOU Jia-yi，SHEN Meng-jie，SHEN Feng-liang
（Institute of Precision Machinery，Zhejiang Normal University，Jinhua 321004，China）

In order to improve the precision of closely wavelet ridge extracted by conventional method，a new method for extracting closely wavelet common ridge based on phase extraction is proposed.The common-ridge phase characteristics of close single frequency signals and frequency modulated signals are fully analyzed，then a common ridge extraction method is put forward based on phase extraction，and finally the problems in signal reconstruction is solved.The proposed method is simple，accurate and with rapid convergence.The results of simulation example show that the proposed method is feasible and effective.Finally，the result of gearbox analysis shows that this method can extract fault characteristics of gearbox effectively.

wavelet ridge；phase method；closely ridge；wavelet transform

HT165.3；TP277；TN911.2；TP301.6

A

1674-5124（2013）03-0001-05

2012-11-14；

：2013-01-09

国家自然科学基金项目（51277166）浙江省自然科学基金项目（LQ12E07002）新苗人才计划项目（2012R404020）

蒋永华（1982-），男，浙江诸暨市人，讲师，博士，主要从事信号分析与处理、状态监测与故障诊断。