基于自适应QPSO算法的软件测试数据自动生成

蹇红梅，成新文，曾燕

（四川理工学院计算机学院，四川自贡 643000）

基于自适应QPSO算法的软件测试数据自动生成

蹇红梅，成新文，曾燕

（四川理工学院计算机学院，四川自贡 643000）

针对软件测试数据采用遗传算法和粒子群算法自动生成算法复杂和容易早熟等问题，提出一种动态调整收缩扩张因子的自适应量子粒子群算法（AQPSO）。该算法通过引入粒子进化度和聚合度，收缩扩张因子随粒子进化度因子和聚合度因子变化而变化，从而实现算法的动态自适应性，提高算法收敛速度和求解精度。软件测试数据自动生成实验验证了该算法的有效性和可行性。

量子粒子群；软件测试；测试数据生成；收缩扩张因子

0 引言

软件测试在软件生命周期中占有十分重要的地位，它是保证软件质量的重要手段，良好的软件测试数据对于程序错误的发现至关重要。在实际测试过程中，若采用人工方式构造测试数据，时间花费巨大并且效率低下。自动生成测试数据可以有效地降低测试人员的工作强度，提高软件测试效率，一直被广泛研究。

近年来，智能优化算法开始用于测试数据的自动生成。文献[1]将遗传算法应用于测试数据的自动生成；文献[2]提出了适应值函数构造的“分支函数叠加法”。傅博[3]将模拟退火算法与遗传算法结合，取得了一定成果；李军等[4]提出了自适应遗传算法，通过自适应改变交叉率和变异率，提高了算法的覆盖率；夏芸等[5]对遗传算法进行改进，提出了一种基于IGA（免疫遗传算法）的测试数据自动生成方法，有效改善了遗传算法的未成熟收敛缺陷。由于遗传算法存在算法复杂、参数设置复杂的问题，李爱国等[6]提出了一种基于粒子群算法的软件结构测试数据自动生成方法。

但是，粒子群优化算法生成测试数据存在容易产生早熟收敛而陷入局部最优的问题。文献[7]提供了量子行为粒子群（QPSO）算法，其全局搜索性能远远优于一般PSO算法。

本文将QPSO算法应用于软件测试数据自动生成，在文献[8]的基础上提出了基于QPSO的自适应算法（AQPSO）。该算法的收缩扩张因子随粒子进化度和聚合度变化而变化，实现了算法的动态自适应性。

1 粒子群算法

1995 年，美国社会心理学家Kennedy博士和电气工程师Eberhart博士提出了粒子群优化算法（PSO）[9-10]。粒子群优化算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。

如果xi=（xi1，xi2，…，xiD）为D维目标搜索空间中粒子i的当前位置；νi=（νi1，νi2，…，νiD）为第i个粒子的当前“飞行”速度；pbest=（pi1，pi2，…，piD），i=1，2，…，N为粒子i所经历过的具有最好适应值的位置（个体极值），整个粒子群迄今为止搜索到的最优位置（全局极值）为gbest=（pg1，pg2，…，pgD）。粒子更新自己的速度和位置的方法如下：

式中：c1，c2——加速常数；

w——惯性权重；

r1，r2——两两相互独立的[0，1]范围内变化的随机数。

由于PSO算法简单容易实现并且没有太多的参数调节，目前已被广泛应用于函数优化、神经网络训练、模糊系统控制以及其他遗传算法的应用领域。但是，PSO算法具有搜索空间有限、容易陷入局部最优解的缺陷。

2 采用的算法思想和策略

2.1 量子粒子群算法

在量子空间中，粒子的位置和速度不能同时确定，因此粒子的状态可以通过波函数来描述。波函数模的平方是粒子在空间中某一点出现的概率密度，并通过求解薛定谔方程得到粒子在空间某一点出现的概率密度函数，随后通过蒙特卡罗随机模拟的方式得到量子空间中粒子的位置方程，如下式所示[7]：

式中：p（t）——P（t）与G（t）之间的随机位置；

P（t）——上一代所有粒子的个体最佳位置；

G（t）——上一代群体的最佳位置；

C（t）——上一代所有粒子个体最佳位置P（t）的平均值；

M——粒子个数；

α——收缩扩张因子，在算法收敛的过程中线性减小；

it——当前迭代次数；

itmax——设定的最大迭代次数；

X（t+1）——粒子的当前位置；

φ（t），u（t）——0～1之间的随机数，如果u（t）≥0.5时，式（4）则取“-”号，当0＜u（t）＜0.5时，式（4）取“+”号。

2.2 自适应策略和边界处理策略

量子粒子群算法的收敛性能与收缩扩张因子α的选择和控制密切相关。从式（5）可以看出，在粒子进化过程中，随着进化代数的增加收缩扩张系数α线性减小，这种变化并不能自适应避免早熟趋势。

为此，引入粒子进化度和粒子聚合度两个粒子群动态性能指标[11-13]。粒子进化度（degree of evolutionary）描述粒子群的进化速度，表明本次迭代当前的全局最优值优于前一次迭代全局最优值的程度；粒子聚合度（degree of aggregation）描述粒子群所有粒子的聚集程度，当所有粒子都达到全局最优值时，粒子群聚集为一个点。

对于适应度函数最小化优化问题，其粒子进化度和粒子聚合度的定义式如下：

式中：f（（xg（t））——第t代粒子群全局最优值；

f（xi（t））——粒子i的个体最优值；

N——粒子总量。

根据粒子进化度定义式（7）可知0＜e≤1，e越小粒子进化速度越快，粒子的集中性越小。在程序运行早期，e较小，粒子可以在较大的空间内搜索，随着程序运行e逐渐增大，e较大时可以减少α使得粒子在小范围内搜索，以便更快地找到最优值，直到e为1时为止。

根据粒子聚合度定义式（8）可知0＜β≤1，β越大，则粒子群聚集程度越大，粒子的多样性越小。程序运行早期β较小时，粒子比较分散，粒子的多样性大，粒子不易陷入局部最优；随着程序运行β增大，多样性减少，算法容易陷入局部最优值，此时需要增大β从而增大搜索空间，提高粒子群全局寻优能力。

根据上述分析，QPSO算法的收缩扩张因子α应随粒子进化度增大而减小，随粒子聚合度β增大而增大。因此，基于粒子进化聚合度的收缩扩张因子计算方法如下所示：

式中：e——粒子进化度因子；

β——粒子聚合度因子；

α0——收缩扩张因子初始值，一般取α0=1.0，b=0.5，c=0.1。

从而实现了基于粒子进化聚合度的收缩扩张因子动态自适应调整的AQPSO算法。

上述AQPSO算法，粒子有时可能会飞出有效的搜索空间，为解决此问题，在实验中设计了“随机回缩法”的边界处理策略。

“随机回缩法”的基本思想是：当粒子位置大于最大边界位置时，将其随机回缩到中心与最大边界之间；当粒子位置小于最小边界时，将其随机回缩到中心与最小边界之间。更新后的粒子新位置计算方法如式（10）：

式中：xmax——粒子的最大边界位置；

xmin——粒子的最小边界位置。

2.3 适应值函数的构造策略

在基于量子粒子群优化算法的测试数据集自动生成算法中，一个粒子代表一个测试数据，一次产生一个测试数据集。适应值函数是QPSO应用于求解问题的优化目标，它的构造直接影响QPSO在具体问题上的运行效率。

可以采用“分支函数叠加法”来构造QPSO的适应值函数[2]。分支函数是一个分支谓词到实际值的映射，可以定量描述在测试数据的驱动下，被测单元的实际执行路径对选定路径的覆盖程度。在测试程序选定路径上的各分支点前进行分支函数的插桩。

假定分支谓词为简单关系表达式（不等式和等式），则分支谓词和其对应的等式谓词描述形式如下：

其中，分支函数F为一个实值函数，分支函数的构造方法如表1所示。

对于分支谓词通过“And”或“Or”构成的逻辑运算，其分支函数构造形式为Max（F1，F2）。

如果在选定路径上，有n个分支点，m个输入参数，则n个分支函数构成的分支函数集为由分支函数叠加构成该路径的评价函数为

表1 分支函数的构造

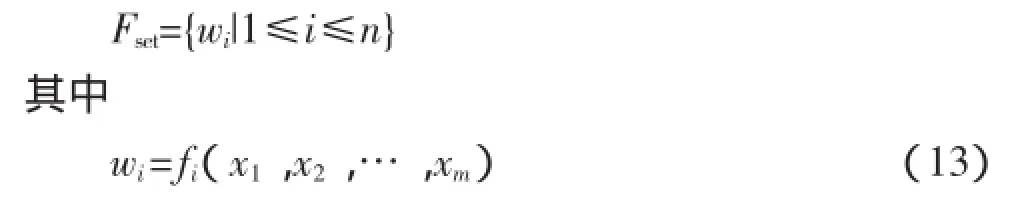
评价函数的插入位置与分支函数的插桩位置不同，通常位于程序的结束位置处。

2.4 基于AQPSO的软件测试数据自动生成策略

基于AQPSO的测试数据自动生成方法，将测试数据作为粒子群向量X的元素。首先随机生成测试数据，然后用AQPSO算法搜索符合指定路径的测试数据，使得适应值函数的值达到最小。AQPSO算法不仅参数随机性强，个数少，并且能覆盖所有解空间，保证算法的全局收敛性。该算法生成测试数据的具体实现步骤如下：

（1）分析被测的软件程序，确定适应值函数，对被测程序进行插桩。

（2）设定粒子数M，维数Dimension，最大允许迭代次数MAXTIER。在问题空间中，初始化粒子群中每一个粒子的当前位置Xi（0），并设置个体的最好位置Pi（0）=Xi（0），设置迭代次数计数器t=0。

（3）根据式（4）计算粒子群中的平均最好位置。

（4）对于粒子群中的每一个粒子i（1≤i≤M），执行（5）～（8）。

（5）按照式（14）计算粒子i的当前位置Xi（t）的适应值，更新粒子的个体最好位置Pi（t），即将Xi（t）适应值与前一次迭代Pi（t-1）的适应值比较，如果Xi（t）适应值优于Pi（t-1）的适应值，则置Pi（t）=Xi（t），否则，Pi（t）=Pi（t-1）。

（6）对于粒子i，将Pi（t）的适应值与全局最好位置G（t-1）的适应值进行比较，若优于G（t-1）的适应值，则置G（t）=Pi（t）；否则Pi（t）=Pi（t-1）。

（7）对粒子的每一维，根据式（3）计算得到一个随机点的位置。

（8）按式（9）计算收缩扩张因子，根据式（6）和式（10）计算和更新粒子位置。

（9）若算法的终止条件不满足，置t=t+1，返回步骤（2），否则算法结束。

3 实例验证

三角形判别问题的程序包含了清晰而又复杂的逻辑，从而在软件测试数据生成中广泛使用。为了验证AQPSO算法自动生成软件测试数据的可行性，采用了与文献[6]相同的直角三角形判定典型测试实例，并用一组统计数值来衡量算法的性能。硬件平台为Lenovo扬天A4600K，Pentium Dual-Core E5800@ 3.2GHz，2G内存。算法程序在Matlab R2010b中测试验证。

表2提供了AQPSO算法、GA算法及PSO算法找到最优解的迭代次数比较数据。粒子数目和种群数从100到280之间变化，实验中对每个粒子数和种群数各运行10次。表中记录了10次运行中找到最优解迭代次数的最好、最差及平均值。

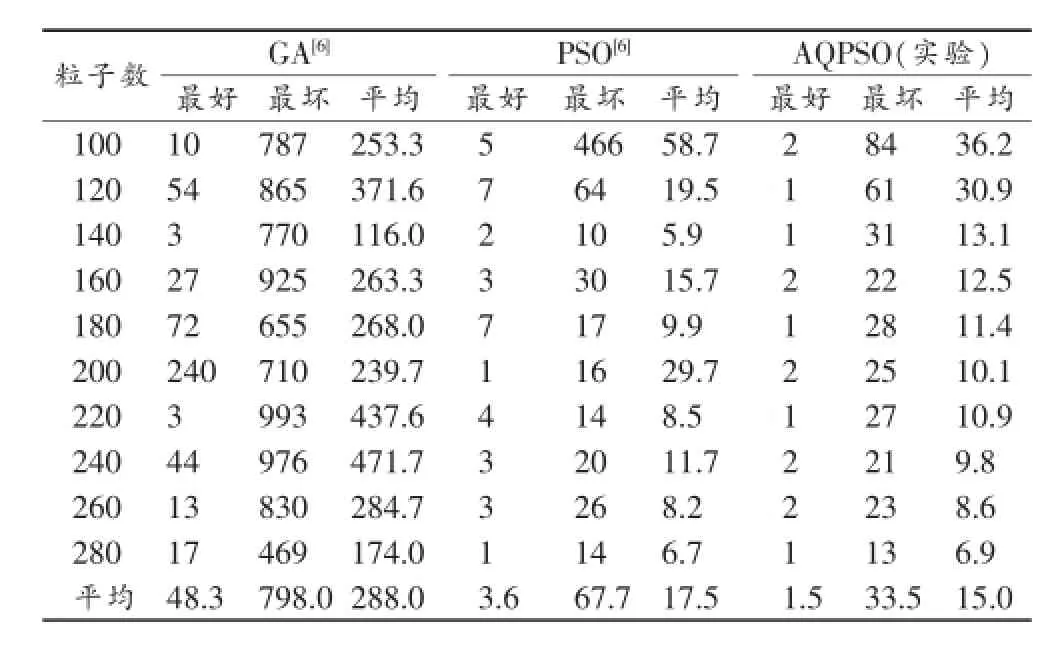
表2 3种生成直角三角形测试数据算法找到最优解的迭代次数比较

根据表2数据进行分析比较：

（1）分析GA、PSO和该实验的AQPSO 3种算法找到最优解（生成所需的测试数据）的迭代次数。根据平均值统计情况进行分析，在最好情况下，PSO算法的迭代次数约是GA算法的1/13，AQPSO算法的迭代次数约是GA算法的1/32，PSO约是AQPSO的2.4倍；在最坏情况下，PSO算法的迭代次数约是GA算法的1/12，AQPSO约是GA算法的1/24，PSO算法约是AQPSO算法的2倍；从平均迭代次数分析，PSO算法的迭代次数约是GA算法的1/16，AQPSO算法的迭代次数约是GA算法的1/19，PSO算法的迭代次数约是AQPSO算法的1.2倍。AQPSO算法的收敛速度均高于PSO算法和GA算法。

（2）分析GA、PSO和该实验的AQPSO 3种算法找到最优解的迭代次数稳定性。GA算法的最好迭代次数从第3代到240代，相对于迭代平均值48.3变化幅度很大；PSO的最好迭代次数从第1代到7代，相对于迭代平均值3.6变化幅度下降，最好迭代次数较稳定；AQPSO的最好迭代次数大多为第1代或第2代，最好迭代次数最稳定。从3种算法最优解的平均迭代次数分析，也可得到同样的结果。

总之，采用本文所述方法生成直角三角形测试数据的效率和稳定性均明显高于粒子群算法PSO和遗传算法GA。

4 结束语

针对遗传算法生成软件测试数据存在参数多、算法复杂以及标准粒子群算法容易早熟而陷入局部最优问题，引入自适应量子粒子群优化算法（AQPSO）。该算法改变了标准量子粒子群算法收缩扩张因子线性变化难以自适应避免早熟趋势的缺点。通过粒子进化度和聚合度自适应动态调整收缩扩张因子，从而实现了算法的动态自适应性，提高了算法的收敛速度和求解稳定性。软件测试数据自动生成实验验证了算法的有效性和可行性，扩展了量子粒子群算法应用范围。

[1]Hermadi I，Ahmed M A.Genetic algorithm based test data generator[C]∥Evolutionary Computation，2003.

[2]Korel B.Automated software test data generation.Software Engineering[J].IEEE Transactions，1990，16（8）：870-879.

[3]傅博.基于模拟退火遗传算法的软件测试数据自动生成[J].计算机工程与应用，2005（12）：82-84.

[4]李军，李艳辉，彭存银.基于自适应遗传算法的路径测试数据生成[J].计算机工程，2009，35（2）：203-205.

[5]夏芸，刘锋.基于免疫遗传算法的软件测试数据自动生成[J].计算机应用，2008（3）：723-725.

[6]李爱国，张艳丽.基于PSO的软件结构测试数据自动生成方法[J].计算机工程，2008（6）：93-94，97.

[7]Sun J，Feng B，Xu W B.Particle swarm op tim ization with particles having quantum behavior[C]∥Proceedings of Congress on Evolutionary Computation，2004：325-331.

[8]赵吉，孙俊，须文波.一种求解多峰函数优化问题的量子行为粒子群算法[J].计算机应用，2006，26（12）：2956-2960.

[9]Kennedy J，Eberhart R.Particle swarm optimization[C]∥Proc of IEEE International Conference on Neural Networks.Perth：IEEE Press，1995：1942-1948.

[10]朱小六，熊伟丽，徐保国.基于动态惯性因子的PSO算法的研究[J].计算机仿真，2007，24（5）：154-157.

[11]任子晖，王坚.一种动态改变惯性权的自适应粒子群算法[J].计算机科学，2009，36（2）：227-229.

[12]黄泽霞，俞攸红，黄德才.惯性权自适应调整的量子粒子群优化算法[J].上海交通大学学报，2012（2）：228-232.

[13]陈翔.一种基于粒子群优化的成对组合测试算法框架[J].软件学报，2011（12）：2879-2893.

Automatic generation of software test data based on adaptive QPSO algorithm

JIAN Hong-mei，CHENG Xin-wen，ZENG Yan
（School of Computer Science，Sichuan University of Science&Engineering，Zigong 643000，China）

For the complexity and prematurity of the automatic software test data generation algorithm based on the genetic algorithm and the standard particle swarm optimization algorithm，an adaptive quantum-behaved particle swarm optimization（AQPSO）algorithm is presented to dynamically adjust the contraction expansion factro to overcome these shortcomings.By introducing the evolution degree and polymerization degree of the particle into this method，the contraction expansion factor keeps changing as the evolution dgree and polymerization dgree factors are changing，orderly the dynamical and adaptive algorithm is realize，which improves the convergence speed and precision the traditional algorithm.The experiment on automatic generation of software test data verified the validity and feasibility of the algorithm.

QPSO；software testing；test data generation；contraction expansion factor

TP206+.1；TP301.6；TP311.52；TP311.55

A

1674-5124（2013）03-0100-04

2012-11-07；

：2013-01-08

四川省教育厅科研基金项目（10ZC084）人工智能四川省重点实验室科研基金（2008RK010）

蹇红梅（1980-），女，四川南充市人，讲师，硕士，研究方向为计算机应用与软件测试。