M型电磁传感器检测裂纹的仿真分析及参数优化

左宪章，钱苏敏，张云，常东

（军械工程学院无人机工程系，河北石家庄 050003）

M型电磁传感器检测裂纹的仿真分析及参数优化

左宪章，钱苏敏，张云，常东

（军械工程学院无人机工程系，河北石家庄 050003）

传统的脉冲涡流传感器采用圆柱式结构，其磁场大部分在空气中传播，造成能量的损失，因此该文设计M型电磁传感器在单线圈传感器上增加一个U型磁轭来提高磁场的利用率。通过ANSYS仿真软件对M型传感器与单线圈传感器检测不同深度的裂纹进行仿真对比，结果证明M型传感器的灵敏度高，信号强，同时对于传感器激励源参数进行优化。

脉冲涡流；M型传感器；裂纹检测；参数优化

0 引言

在裂纹缺陷检测中，传统的无损检测方法有超声、磁粉和渗透等，但超声检测需要用到耦合剂，磁粉和渗透检测对工件表面要进行一些预处理。而近期的研究热点脉冲漏磁及脉冲涡流检测技术，对工件表面状况要求低，易于检测，因此逐步在裂纹检测中占据主导地位。脉冲漏磁检测主要针对的是铁磁性材料，而脉冲涡流检测主要针对的是非铁磁性材料，但是在检测铁磁性材料时，也有涡流成分的存在，所以研究利用脉冲涡流技术检测铁磁性材料裂纹将使这一技术得到更大的运用前景[1-2]。

传统的脉冲涡流传感器采用圆柱形传感器，激励线圈使被检试件内部产生所需磁场，磁场大部分是在空气中传播，而空气的磁导率很低，这就导致磁场在空气中会有很大衰减，造成磁场能量的损失，对于检测精度会有很大程度的影响。

本文主要研究M型脉冲涡流传感器对铁磁性材料的裂纹检测。通过ANSYS有限元仿真的方法，对M型传感器模型与单线圈传感器模型进行了仿真对比，验证了传感器的有效性，同时对于传感器激励源参数进行了优化。

1 仿真实验对比

1.1 脉冲涡流检测原理

涡流检测方法是将通有交变电流的线圈靠近待测试件，而线圈中的交变磁场与试件发生电磁感应，在导体中感生出涡流，涡流也会产生感应磁场。当试件表面有缺陷时，会导致涡流与感应磁场的强度与分布的变化[3]。与传统的涡流检测技术相比，脉冲涡流利用一个重复的宽带脉冲（例如方波）激励线圈，线圈中产生瞬时电流，在检测对象上感应出瞬时涡流，并与快速衰减的磁脉冲结合起来在材料中传播，且脉冲包含了很宽的频谱，所以感应信号中包含大量的信息[4-5]。

在传统的脉冲涡流传感器结构中，激励线圈产生的磁场通过线圈下端到达工件，然后通过空气耦合回到线圈上端，从而形成磁路。因此激励磁场除了在所测试件内部产生所需的磁场，同时大部分磁路暴露在空气中，衰减大，使得通过试件的磁场很微弱，所产生的磁场强度较弱，导致检测灵敏度低。本文拟提出一种新型传感器励磁结构——M型脉冲涡流传感器，保证励磁磁路大部分集中在铁磁材料中进行传播，因而相比于传统的圆柱型的传感器，能量损失小、检测灵敏度高。

1.2 M型传感器结构设计

通过有限元软件ANSYS，建立传感器的模型。激励线圈位于M型铁芯中间的磁极上，当激励线圈产生的磁场通过无缺陷的试件时，磁场通过M型磁轭的另外两磁极和试件形成闭合回路，磁场均匀分布。

设计M型传感器长44mm，宽20mm，高28mm。其中，中间的磁轭长12mm，宽20mm，高20mm。单线圈传感器长12mm，宽20mm，高20mm。线圈匝数为400匝。试件长70mm，宽20mm，高度5mm，如图1和图2所示。

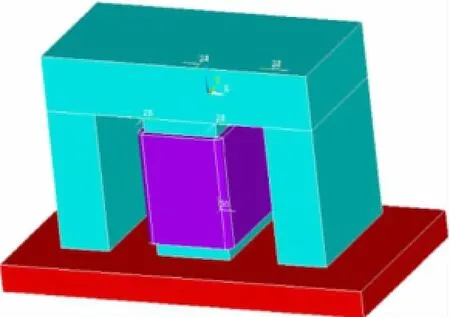
图1 M型模型

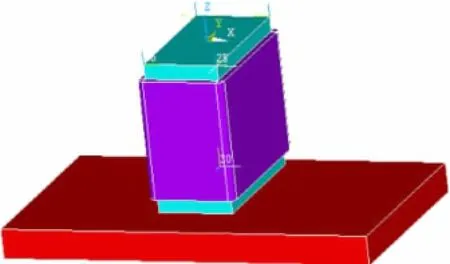
图2 单线圈模型

所建立的模型包括线圈、磁轭、试件与空气。线圈电阻率为1.75E-8Ω·m，相对磁导率为1。磁轭相对磁导率为1000。试件电阻率为2E-7Ω·m，相对磁导率为200，为铁磁性材料。对于激励线圈施加的是占空比为50%，频率为50Hz，激励电流为4A的方波。

当传感器与工件提离值为1mm时，传统圆柱型传感器与M型传感器激励磁场磁通密度及试件上涡流分布仿真结果如图3、图4、图5、图6所示。

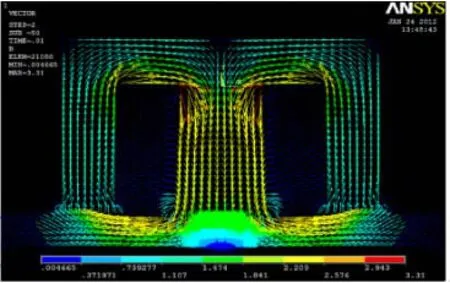
图3 M型传感器激励磁通密度分布

图4 单线圈传感器激励磁通密度分布

图5 M型传感器励磁的工件涡流分布

图6 单线圈传感器励磁的工件涡流分布

由图3和图4可知，M型传感器激励磁场在各方向上的分布是不均匀的，相对集中在有磁轭的位置上，所产生的涡流也是不均匀的，左右位置附近涡流密度较大，前后涡流密度相对较小，如图5所示。单线圈传感器由于磁场在空气中均匀传播，所以涡流密度分布相对均匀，如图6所示。在M型线圈中，磁通密度最大值为3.31T，涡流密度最大值为0.004 665T，而单线圈中磁通密度最大值为0.545681T，涡流密度最大值为0.001658T。可见，单线圈产生的涡流密度最大值比M型传感器产生的涡流密度最大值小，这是由于在空气中磁场没有在磁轭中分布密集，因此，M型传感器在检测相同位置的缺陷时所得数据大，更易于检测。

1.3 信号特征分析

图7显示了铝材料工件的传统典型的脉冲涡流参考信号、检测信号以及它们相减得到的差分信号。参考信号和检测信号趋势相同，都是起始段急剧上升到接近最大值，之后缓慢的趋于某一极限值。差分响应信号起始段上升不如前两种信号快，到达最大值点后，先快速后缓慢的下降，到趋于零点。在峰值点处，检测信号和参考信号的差别最大。通常采用的信号特征为差分信号的峰值及峰值时间[6-7]。

图7 铝材料的脉冲涡流信号

通过仿真，将试件换成铁磁性材料时，在提离0.2mm处，分别提取无缺陷与存在缺陷深0.2mm、宽1mm的中心位置的瞬态磁通密度值，如图8所示。

图8 检测铁磁材料瞬态磁通密度

通过图8可知，当检测铁磁性材料时，测得的磁场最大值受磁化效应[8]和铁磁材料的磁质特性的影响。图9中显示的磁场是由激励产生的磁场以及由涡流产生的磁场叠加而成的。由于磁场会向磁导率大的方向流动，所以在缺陷周围，磁场会向工件处流动，而在空气中流动的磁场减少，磁场不均匀分布。无缺陷时，产生的磁场是均匀分布。所以采集的无缺陷处的参考信号幅值与检测信号幅值最终无法达到一致。同时，当达到稳定的时候，无缺陷的B的稳定值相比于有缺陷的B的稳定值大。这与非铁磁性材料有很大区别。

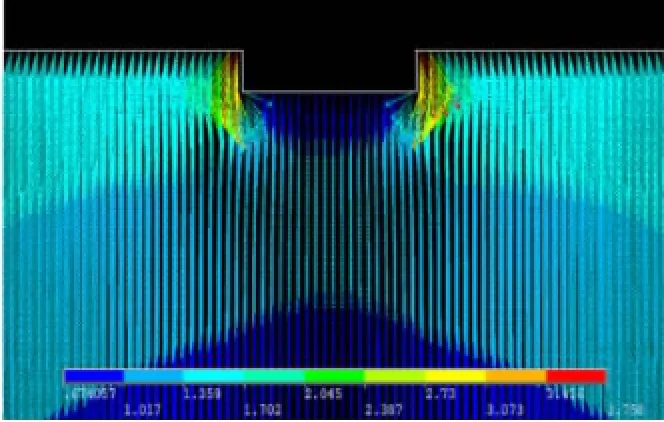
图9 缺陷附近磁通密度分布

所以引入归一化的差分信号ΔBnorm=B/max（B）-BREF/max（BREF），其中B/max（B）是归一化后的检测信号，BREF/max（BREF）是归一化后的参考信号。虽然磁导率对于B有影响，但是由于归一化，ΔBnorm明显的减少了磁导率对其的影响。图10所示为缺陷的归一化差分信号。提取信号的峰值以及峰值时间作为特征量。

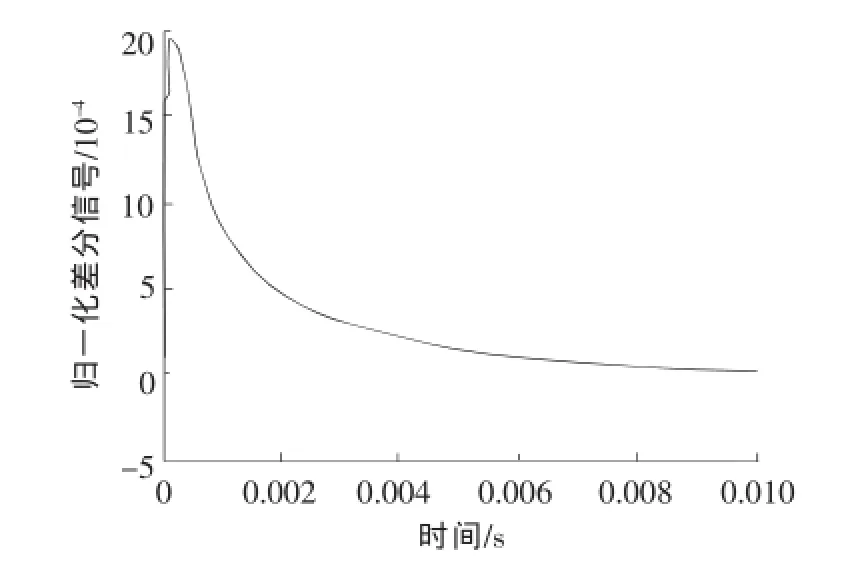
图10 0.2mm归一化差分信号

1.4 仿真结果分析

利用M型线圈与单线圈分别对于无缺陷，缺陷宽都为1mm，缺陷深分别为0.2，0.4，0.6，0.8，1mm进行仿真。通过归一化差分的处理，所得结果如图11和图12所示。

提取信号的峰值及峰值时间，所得数据如表1所示。根据表1，可绘出图13与图14。

图11 M型不同深度缺陷的归一化差分信号

图12 单线圈不同深度缺陷的归一化差分信号

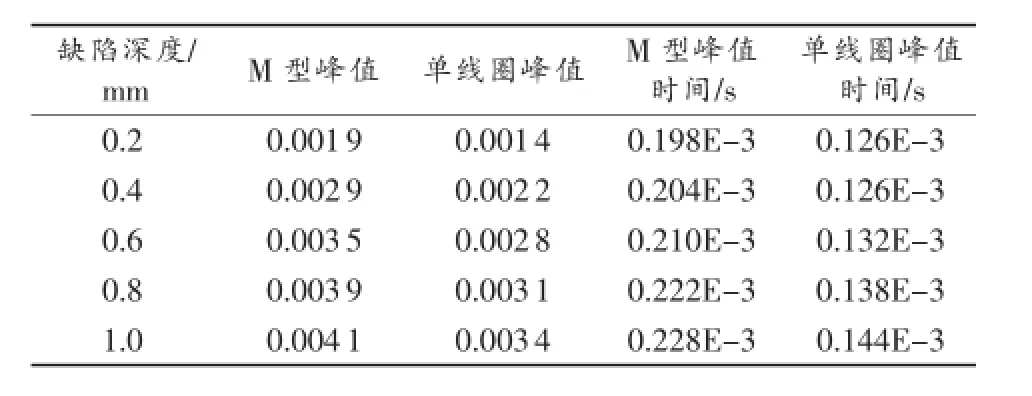
表1 不同缺陷的峰值及峰值时间

图13 M型与单线圈不同深度缺陷归一化差分信号峰值

图14 M型与单线圈不同深度缺陷归一化差分信号峰值时间

从表1及图13、图14可知，M型传感器所得信号相比于单线圈所得的信号峰值较大，两者之间差值最小为0.0005，最大为0.0008。且达到峰值的时间也较大，同时达到峰值的时间差最小为0.006ms，而单线圈达到峰值的时间差最小为0，即无时间差。可见，M型传感器对于宽度相同、深度不同的缺陷检测比单线圈传感器灵敏度更高，信号更强，利于检测。

2 模型激励源参数的优化

为了进一步增加传感器模型的检测精度，针对M型传感器进行了参数优化。设置缺陷深度为0.2mm，宽度为1mm，对于不同激励源频率及激励源大小进行仿真，选取最佳参数。

2.1 激励源频率的选择

在脉冲激励大小以及占空比不变的前提下，改变脉冲激励源的频率并采集其缺陷信号峰值大小，绘制曲线如图15所示。

图15 不同频率下的磁通密度峰值

可以看出，随着激励源频率的增加，缺陷信号峰值不断减小，因为随着脉冲激励频率的增加，其激励电流正负交替频率变快，稳定值时间变短，试件充磁不充分，产生的涡流变小，磁场叠加不明显，所测的数据也减小。所以脉冲涡流检测不适宜高频的情况下，在选择激励电源的频率时，一般选择100Hz以下。

2.2 激励源大小的选择

在脉冲激励占空比以及频率不变的前提下，改变激励源的大小并采集其缺陷信号峰值大小，绘制曲线如图16所示。

图16 不同激励源大小下的磁通密度峰值

从图16可知，随着激励源大小的增大，峰值的大小也随之增大。因此，在保证试件不被磁饱和的情况下，应尽量选择大的激励源。

3 结束语

通过研究脉冲漏涡流传感器的结构，提出了新型的M型传感器，利用ANSYS有限元仿真的方法，对M型传感器模型与单线圈传感器模型进行了仿真对比。结果显示，M型传感器的检测信号强，灵敏度高。并进一步对其激励源参数进行了优化，为以后的实验平台搭建打下基础。

[1]Huang C，Wu X J，Xu Z Y，et al.Pulsed eddy current signal processing method for signal denoising in ferromagnetic p late testing[J].NDT&E International，2010（43）：648-653.

[2]Huang C，Wu X J，Xu Z Y，et al.Ferromagnetic material pulsed eddy current testing signal modeling by equivalentmultiple-coil-coupling approach[J].NDT&E International，2011（44）：163-168.

[3]游凤荷，蒋韬，孙研飞.脉冲涡流磁场特征分析[J].仪表技术与传感器，2003（5）：38-39.

[4]Huang C，Wu X J，Xu ZY，et al.Ferromagneticmaterial pulsed eddy current testing signal modeling by equivalent multiple-coil-coupling approach[J].NDT&E International，2011（44）：163-168.

[5]Xu P，Huang S L，Zhao W.A new differential eddy current testing sensor used for detecting crack extension direction[J].NDT&E International，2011（44）：339-343.

[6]周德强，张斌强，田贵云，等.脉冲涡流检测中裂纹的深度定量及分类识别[J].仪器仪表学报，2009，30（6）：1190-1194.

[7]Sophian A，Tian G Y，Taylor D，et al.A feature extraction techniques for pulsed eddy current NDT[J].NDT E Int，2003，36（1）：37-41.

[8]He Y Z，Luo F L，Pan M C，etal.Defect classification based on rectangular pulsed eddy current sensor in different directions[J].Sensors and Actuators A，2010（157）：26-31.

Simulation analysis and parametric optim ization of M-type pulsed eddy current sensors to detect cracks

ZUO Xian-zhang，QIAN Su-min，ZHANG Yun，CHANG Dong
（Department of UAV Engineering，Ordnance Engineering College，Shijiazhuang 050003，China）

The single-coil sensor was used as the traditional pulsed eddy current sensor，but the magnetic field mostly spreads in the air，resulting in the loss of energy.So a M-type electromagnetic sensor is proposed.The M-type sensor is made of a single-coil and a U-shaped yoke which improved the utilization of the magnetic field.Based on ANSYS simulation，a comparison of the M-type sensor is carried out with the single-coil sensor in detecting the different depths of cracks.The simulation proves the effectiveness of the M-type sensor and the sensor excitation source parameters are optimized at the same time.

pulsed eddy current；M-type sensor；cracks detection；parametric optimization

TP212；TP391.9；TH878；TG115.28

A

1674-5124（2013）03-0065-05

2012-07-12；

：2012-08-30

左宪章（1963-），男，河北石家庄市人，教授，主要从事机械故障诊断及智能信息处理与识别方面的研究。