树状结构引导下的脊线层次划分方法研究

高 翔，徐 柱＊

（西南交通大学遥感信息工程系，四川 成都 611756）

0 引言

不同尺度下的DEM表达不同尺度的地形信息，为获得粗尺度的地形信息，需对精细尺度的DEM进行综合［1－4］，基于结构线的方法能够保证粗尺度下的DEM充分保留原始地形的骨架结构，因此常采用该方法实现尺度转换［5，6］。首先需获得具有层次的山谷线与山脊线［7］，即需对谷线与脊线实施分级。对于山谷线，其层次划分方法已较为成熟［8－10］。对于山脊线，主要有基于分形的方法与基于图论的方法。基于分形的方法［8，11－17］优点在于与地理学中的分形理论相契合，缺点在于难以采用简单的数据结构表达地形特征线。基于图论的方法能较好地克服这一缺陷，将特征线表达为图中的节点，将线段间的拓扑联通关系表达为节点的连接边，以此将复杂的地形特征结构转换为计算机易于实现的图结构。现阶段，众多学者已采用这一方法实现了水网结构的层次划分［18，19］，鉴于脊线与水网在地形中呈现出某种程度的结构相似性，因而，同样可以借用图论方案研究脊线中的层次结构。

为利用图论方案构建脊线层次，需要确定脊线段间的层次关系。传统的树结构层次划分方案有3种：基于长度的层次划分法［20］、基于角度逼近的层次划分法［21］和谷线耦合分层法［22］。前两种层次划分方案尝试利用脊线的几何形态对线段的层次等级进行评估，从地理学的角度考虑，现实地表中的脊线主干线段长度并不一定大于支干，主干线段间的连接形态也并非总是逼近于直线，因而这类方案并不适合。与前两种方案相比，第三种层次划分策略地理学意义更强，然而该方法最大的缺陷在于脊线的层次确定过程极大地依赖于谷线的分级结果，谷线的分级方法较多，不同方案下其分级结果不尽相同，得到的脊线层次也将随之改变，这使得脊线的分级过程存在较大的不确定性，无法为实际应用提供准确、唯一的数据支撑。脊线的分形结构虽与谷线共轭，但其分级应是一个面向其自身结构的、独立式的过程。考虑到脊线等级越高，其在地表中的覆盖范围越广，这在结构上表现为整体跨度越大。

基于这一地理学意义，本文提出一种新的山脊线层次划分方案。首先从脊线自身的拓扑结构出发，将脊线表达为具有多个根节点的二叉树，用树的深度对脊线的区域跨度进行丈量，从而将脊线的层次划分问题转换为树的主支干判别问题，并从脊线拓扑结构的表达与树的主干搜索两个角度对层次划分过程进行论述。实验部分分别从脊线层次划分结果、分级算法效率及不确定性扰动效应三方面对新方法的有效性进行验证。

1 层次划分研究

1.1 脊线树的构建

脊线中的一级主干与一个或多个二级主干相连，二级主干与一个或多个三级主干相连，多叉树能够很好地表达这一分形特征。树中的节点表示地理实体中的脊线段，节点间的联通关系用以表达脊线段的拓扑结构。

由于脊线中不存在地理意义上的出入口，且脊线本身不具有流向信息，基于这一无向的拓扑结构构建多叉树，首先需确定脊线的根节点位置。考虑到脊线两端的线段通常距离流域出口最近，为简单起见，选用脊线段集合中距离流域出口最近的线段作为根节点。然后，逐一计算与其相连的脊线段，并将其作为当前节点的子节点，重复执行该过程直到将所有脊线段纳入至多叉树中。研究发现，队列能够很好地模拟上述过程，具体的实现方法为：1）将当前节点插入至队列中，计算与其联通的节点，并将这些节点标记为当前节点的子节点；2）将当前节点从队列中移除，同时将其子节点插入至队列中；3）重复执行第二步，直到完成子树中所有节点的处理；4）搜索新的根节点，跳转至第一步，进行新一轮的广度优先遍历，直到所有脊线段均处理完成。图1进一步描述了脊线树的构建过程，当前子树共有9条脊线段，首先从集合中选取距离流域出口最近的脊线段（1号线段）作为树的根节点并加入至队列中，接着，搜索与1号线段相连的2号与3号子线段，将其加入至队列中，同时将1号线段从队列中移除，这一过程将反复执行，直到完成所有线段的遍历。

1.2 脊线的分层与遍历

完成脊线树的构建后，需基于树结构搜索山脊线的主干与支干从而完成脊线的层次划分。树结构传统的遍历方式是从其根节点处开始逐层向下搜索，然而这一过程需基于线段的重要性程度选取同级子节点，线段重要性程度的确定存在较大的随意性，不同的策略必将导致不一致的重要性确定结果。针对这一点，本文提出一种深度优先的节点选择方案。首先在子树中搜索具有最大深度的叶子节点，之后从叶子节点开始，自下而上逆向遍历，直到搜索至根节点为止。这一遍历路径上所有节点将作为脊线的同级主干，这一过程将反复执行，直到所有节点均被赋予等级。该方法充分利用多叉树特有的结构特征，将父节点与子节点的一对多的联通关系转换为子节点对父节点的一对一的联通关系，所以能够解决传统分级方法存在的缺陷。值得注意的是，当地形较为复杂时，脊线中可能存在少部分具有相同深度的叶子节点，考虑到脊线两端的线段距离流域出口最近，因此，选择至最近流域出口距离最短的叶子节点作为最终的搜索起点。

在上述多级主干的确定过程中，需重点关注采用何种搜索遍历模式。传统的主干搜索模式是对已遍历的节点进行标注，在确定新一级主干时，依次判断当前遍历线段是否已处理，若已处理，则停止搜索，否则，继续后续遍历（后文称之为“节点标注法”）［19］；然而，当地形较为复杂时，树中存储的脊线段较多，这种遍历方式需进行大量重复性的节点判别，从而极大降低脊线的分级效率。为高效确定脊线的层次结构，应最大限度地避免节点遍历的重复性。考虑到当某节点的父节点作为主干成员被删除后，当前节点的父节点为空，该节点将作为新子树的根节点参与至后续的分级过程中，这表明多叉树的分解具有极强的灵活性。为充分利用多叉树的这一特征，采用多级主干抽离方法完成脊线的层次划分，其过程可描述为：1）基于深度优先法确定搜索的起始节点；2）逆向遍历，确定脊线的当前主干，并将其从多叉树中移除；3）分解多叉树，完成新树的重构，继续进行次级主干的搜索。图2进一步描述了脊线树的分解过程：当确定脊线的一级主干＜1－3－6－12＞后，将其从树中移除，多叉树自行分解为3棵子树，并获得二级主干＜2－5－10－21＞、＜24＞、＜13－26＞以及＜7－14－29＞，将二级主干从树中移除，多叉树自行分解为6棵子树，这一过程将持续进行，直到所有脊线段均获得等级。

2 实验分析

2.1 实验样区的选择

实验分别选取SRTM 90 m分辨率与GDEM 30 m分辨率DEM进行山脊线的层次划分研究，第一幅DEM的区域跨度为171 km×114 km，第二幅DEM的区域跨度为：20 km×13 km；同时，地形高差、平均坡度及表面粗糙度数据表明两研究区域在地形起伏与形态复杂度上也存在一定程度的差异（表1）。因而，实验将在不同尺度、不同地形复杂度的区域上进行脊线层次划分方法的探究。

图3为两幅实验区DEM及相应山脊线的提取结果，可见尺度与地表复杂度的不同导致了两幅DEM提取的脊线在整体形态与丰富程度上存在较大的差异。

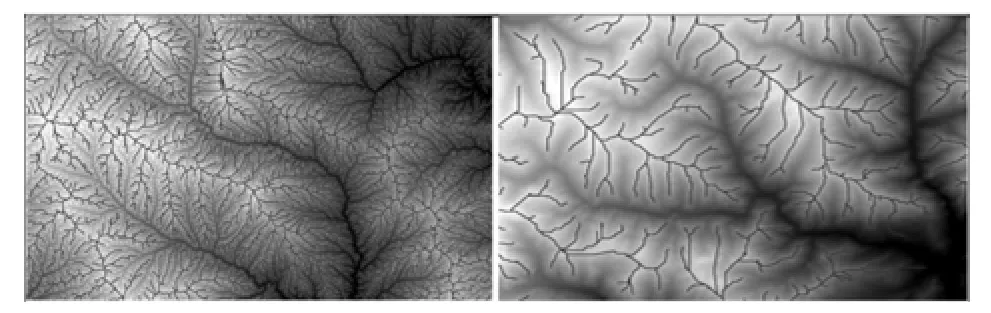
图3 选取DEM及其山脊线（黑色实线）Fig.3 DEM and extracted ridgelines

2.2 脊线的层次划分结果

实验主要从两方面对新的脊线分级方法的有效性进行验证：1）不同分级策略下脊线的层次结构对比；2）不同遍历方式下分级效率对比。本文选取的分级策略分别为长度优先策略、180°角度逼近策略及深度优先策略，选取的遍历方法分别为主干抽离法与节点标注法。两幅实验样区在三种策略下得到的分级结果如图4（见封2）所示，其中图4a－图4c为实验区1不同方法下得到的脊线层次划分结果，图4d－图4f为实验区2不同方法下得到的脊线分层结果。可以发现：1）利用长度优先法与角度逼近法划分脊线等级，得到的层次关系过多，分级结果十分破碎，难以基于结果识别脊线的主干与支干：实验区1在两种方法下得到的脊线等级总数分别为54与44，实验区2在两种方法下得到的脊线等级总数分别为22与15。这两种层次划分方法虽能够在一定程度上完成脊线的分级工作，但破碎的层次关系难以为脊线的主、支干的判读提供实质性的指导；2）无论对于大尺度还是小尺度地形，新方法均能够获得较为理想的层次划分结果：大尺度地形上，深度优先法将脊线划分为5个等级，而在小尺度地形中，该方法则为脊线确定了4个等级，较少的等级数目能够更加清晰直观地表达脊线的层次关系。从图4c、图4d可以发现，新方法搜索出的脊线主干具有最广的覆盖范围，层次越低，其跨越的区域范围也越小。这一实验结果表明，新方法所划分的层次结构不仅具有鲜明的地理学意义，且在表达效果上也优于传统方法。

2.3 层次划分效率分析

为进一步研究新方法的层次划分效率，对实验样区的脊线进行抽稀处理（实验区1的脊线结构更为丰富，因而选用该样区脊线进行效率分析）。抽稀完成后，得到复杂程度各不相同的6组脊线，利用主干抽离法与传统的节点标注法进行脊线等级划分，最终，6组脊线的线段总数以及不同方法下所需的分级时间数据如表2所示。

为进一步研究脊线分级效率随脊线丰富程度的变化情况，绘制两种方法下分级时间随脊线丰富程度的变化曲线，并进行回归拟合（图5）。分析发现：1）两种方法下，脊线分级时间随脊线丰富程度的变化规律相似，当脊线的线段总数较少时，分级时间较小，随着丰富程度的增强，脊线的分级时间迅速增加，这一变化趋势可用幂函数进行拟合。2）当脊线的丰富程度较弱时，两种方法的效率差异较小，随着脊线丰富程度的增强，两种方法的差异性逐渐增大，最终，当线段总数达到2 500左右时，两种方法分级消耗时间相差265 ms。当地形变化程度较为剧烈时，脊线的丰富程度通常较高，此时，主干抽离方法能够更好地保证脊线的分级效率。

2.4 尺度推演中的不确定性对脊线层次划分的干扰性研究

不同尺度下的脊线层次存在某种程度的相似性与统一性，层次划分方法应当对地形简化过程中的不确定性具有较好的抗干扰能力。下面以实验样区1为基础数据，利用地形简化方法获得不同尺度下的地形，并在此基础上研究多尺度下脊线间的层次差异（图6，见封2）。1）建立研究区域的多尺度表面：选用最为常用的Z-tolerance算法提取地形特征点［23］，并构建不同尺度下的地形表面，如图6a－图6c所示；2）提取多尺度表面的山脊线；3）利用层次划分法确定不同尺度下脊线的层次结构，如图6d－图6f所示。实验结果表明：1）随着升尺度过程的进行，地形的细部信息逐渐丢失，与之相对的是，地形脊线的丰富程度逐渐下降；2）随着尺度的上推，脊线丰富程度随之降低，但不同尺度下的脊线主干并未发生明显变化。如图6d中，1级主干拥有2－5级支干，图6e中1级主干拥有2－4级支干，图6f中1级主干拥有2－3级支干。可以发现，随着尺度的推演，脊线层数逐渐减少，但划分得到的主干在整体形态与区域布局上呈现出较强的相似性与统一性。这表明：尺度效应引发的不确定性并未对新方法产生过多的扰动。

3 结论

为准确、高效地获得脊线的层次结构，本文提出一种新的脊线分级方法。首先基于分水岭边界准确提取地形山脊线；利用队列建立其多叉树模型来表达脊线的拓扑结构；利用深度优先算法确定脊线的主干搜索起点，并基于主干抽离模式获得多层次下的脊线主干，从而完成脊线的层次划分。最后，分别从层次划分结果、分级效率以及层次划分对不确定性的抗干扰能力三方面，对新方法的有效性进行验证。结果表明：1）与传统的长度优先法和角度逼近法相比，深度优先方法得到的脊线等级更加简要，表达的脊线层次结构更加清晰；2）当脊线的线性结构较为简单时，其分级效率也较高，随着脊线丰富程度的增加，脊线的分级时间迅速增加，幂函数能够很好地拟合这一变化趋势，同时，与传统的遍历策略相比，本研究采用的主干抽离方法能更好地提升脊线的分级效率；3）尺度上推将影响脊线的丰富程度，但不同尺度上的脊线主干存在相似性与统一性，表明新方法具有较强的不确定性抗干扰能力。

在后续研究中，笔者将继续关注谷线、脊线及水文线这类重要的地形特征线的层次结构研究，并尝试实现一种统一的层次划分机制，从而为地形层次结构研究领域提供一致性更强的科学研究工具。

［1］ ZHANG X，DRAKE N A，WAINWRIGHT J，et al.Comparison of slope estimates from low resolution DEMs：Scaling issues and a fractal method for their solution［J］.Earth Surface Processes and Landforms，1999，24（9）：763－779.

［2］ LI Z L.Multi-scale digital terrain modelling and analysis［A］.ZHOU Q，LEES B，TANG G.Advances in Digital Terrain A-nalysis［C］.Berlin：Springer-Verlag，2008.59－83.

［3］ LI Z L，ZHU Q.Digital Elevation Model［M］.Wuhan：Wuhan University of Surveying and Mapping Press，2003.

［4］ 董有福，汤国安.利用地形信息强度进行DEM地形简化研究［J］.武汉大学学报（信息科学版），2013，38（3）：353－357.

［5］ ZHOU Q，CHEN Y.Generalization of DEM for terrain analysis using a compound method［J］.ISPRS Journal of Photogrammetry and Remote Sensing，2011，66（1）：38－45.

［6］ FEI L，HE J.A three-dimensional Douglas-Peucker algorithm and its application to automated generalization of DEMs［J］.International Journal of Geographical Information Science，2009，23（6）：703－718.

［7］ LI J Z，AI T H，WANG H.The DEM generalization based on the filling valley coverage［J］.Acta Geodaetica et Cartographica Sinica，2009，38（3）：272－275.

［8］ PFAFSTETTER O.Classification of hydrographic basins：Coding methodology［R］.Brazil：Departamento Nacional de Obras de Saneamento，1989.

［9］ GARBRECHT J.Determination of the execution sequence of channel flow for cascade routing in a drainage network［J］.Hydrosoft，1988，1（3）：129－138.

［10］ 刘先龙，杨勤科.流域拓扑关系建立方法研究［J］.水土保持研究，2010，17（3）：82－86.

［11］ STRAHLER A N.Hypsometric（area-altitude）analysis of erosional topography［J］.Bulletin of the Geological Society of America，1952，2（63）：1117－1142.

［12］ 陈于林.基于DEM的水系提取及水系网多级分解［D］.成都：西南交通大学，2006.

［13］ SHREVE R L.Infinite topologically random channel networks［J］.Journal of Geology，1967，75（2）：178－186.

［14］ VERDIN K L，VERDIN J P.A topological system for delineation and codification of the Earth′s river basins［J］.Journal of Hydrology，1999，218（1－2）：1－12.

［15］ 罗翔宇，贾仰文，王建华，等.基于DEM与实测河网的流域编码方法［J］.水科学进展，2006，17（2）：259－264.

［16］ GARBRECHT J.Determination of the execution sequence of channel flow for cascade routing in a drainage network［J］.Hydrosoft，1988，1（3）：129－138.

［17］ 任立良，刘新仁.数字高程模型在流域水系拓扑结构计算中的应用［J］.水科学进展，1999，10（2）：129－134.

［18］ 陈玉芬，李书琴，何东健.流域拓扑结构分析与计算机实现［J］.干旱地区农业研究，2005，23（5）：183－186.

［19］ 刘先龙.基于DEM的流域水文网络建立方法研究［D］.咸阳：西北农林科技大学，2011.

［20］ BRIGGS I.Water Flow Using Desity of Area［R］.1989.1－11.

［21］ 张园玉，李霖，金玉平，等.基于图论的树状河系结构化绘制模型研究［J］.武汉大学学报（信息科学版），2004，29（6）：537－543.

［22］ 贺文慧，汤国安，杨昕，等.面向DEM地貌综合的山脊线等级划分研究——以黄土丘陵沟壑区为例［J］.地理与地理信息科学，2011，27（2）：30－33.

［23］ CHANG K T.Introduction to Geographic Information Systems［M］.Singapore：McGraw-Hill，2008.