多项式变分不等式解集的非空紧性和估计
李 湾,凌 晨
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
多项式变分不等式是张量变分不等式问题[1]和仿射变分不等式的自然延伸,也是多项式互补问题[2]的推广。多项式变分不等式不仅与多项式优化关系密切,而且在控制理论、均衡问题和博弈论等领域有广泛应用[3]。解的存在性、紧性、解的估计和稳定性分析等均是变分不等式问题基本研究内容[4]。1984年,Smith[5]首次提出连续映射例外族概念,用于研究互补问题解的存在性。从此,很多学者运用例外族概念和拓扑度理论研究相关方程、互补和变分不等式问题解的性质[6-7]。2018年,Wang等[1]提出张量变分不等式问题,并研究问题解的存在性、唯一性和有界性等。本文证明了在多项式变分不等式的首项系数张量为正定时其解集为非空紧;在多项式为m-阶强伪单调时,得到了其解的唯一性,并给出一个解的估计。
1 问题描述

本文考虑一类多项式变分不等式问题(Polynomial Variational Inequality Problem,PVIP),即寻找x*∈X,使得
〈y-x*,F(x*)〉≥0,∀y∈X
(1)
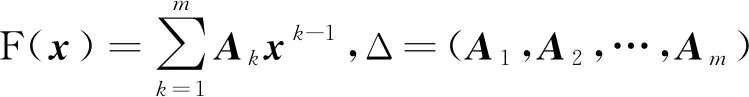
2 预备知识
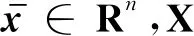


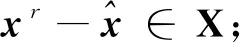
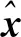


定义3[8]设A∈Tm,n,X⊆Rn为非空集。若对任意x∈X{0},均有Axm>0,则称A是在X上正定的张量。
对给定的A∈Tm,n,定义算子TA∶Rn→Rn如下:
(2)
易知,TA是正齐次算子,即对任意t≥0,均有TA(tx)=tTA(x)。进一步,有如下引理。
引理2[9]对任意x∈Rn,均有
3 主要结果


(3)
由式(3)和正规锥定义,得
(4)
(5)
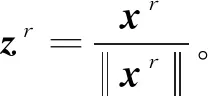
(6)


(7)


定理2[4]设X⊆Rn为非空闭凸集,F∶X→Rn为m- 阶强伪单调,则问题VI(X,F)存在唯一解。



由此和Cauchy-Schwrz不等式,知
即
进一步,由引理2中的结论1,得到

(8)
下面分两种情况讨论。


证毕。
结合定理3和引理2的结论2,得到如下推论。

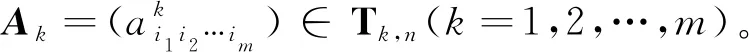
例设A1=0,A2=0和A3=(ai1i2i3)∈T3,2,其中a111=2,a222=1,其余ai1i2i3均为0。设X={x1,x2∈R2|x1≥1,x2=2x1},则易验证F(x)=A3x2在X上是3-阶强伪单调的。事实上,任取不相等的x,y∈X,若〈F(y),x-y〉≥0,则易知x1-y1≥0和x2-y2≥0。

所以F在X上是3-阶强伪单调的。
4 结束语
本文针对多项式变分不等式问题,使用例外族的概念,证明了当多项式函数中首项系数张量在可行域上为正定时,解集为非空紧;进一步,在多项式函数为m- 阶强伪单调时,证明了其解唯一,并给出了解的估计。后续将针对多项式变分不等式问题解的稳定性和误差界条件展开进一步研究。

