基于SOA-SI全光逻辑异或门及或非门的理论研究

邓跃平，李齐良

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

0 引 言

为了满足电信网络的高带宽和低功耗需求，全光信号处理技术的研究引起广泛关注，如全光切换、全光波长转换和全光逻辑操作等。作为全光网络的关键因素，基于半导体光放大器(Semiconductor Optical Amplifier，SOA)和Sagnac干涉仪(Sagnac Interferometer，SI)两种器件结合的全光逻辑门可以实现许多网络功能，包括寻址、报头识别、标签交换和数据包交换等。众所周知，全光逻辑设计方法主要基于光纤[1]、半导体元件[2]和光波导[3]中的非线性效应。在实现各种逻辑功能方面，具有交叉增益调制(Cross Gain Modulation，XGM)效应的SOA成为极具吸引力的非线性器件，加上干涉仪结构的快速处理能力，基于SOA和干涉仪结合的方案可以实现更多的功能，比如，文献[4]将半导体光放大器与超快非线性干涉仪(Semiconductor Optical Amplifier-Ultrafast Nonlinear Interferometer，SOA-UNI)结合，以10 Gb/s速率从短同步数据包中分离出报头和有效载荷；基于半导体光放大器和马赫曾德尔干涉仪(Semiconductor Optical Amplifier-Mach Zehnder Interferometer，SOA-MZI)的研究已实现或门、与门、同或门和异或门等逻辑操作[5-6]；SOA-SI可以实现4位二进制到格雷码和格雷到二进制码转换器[7]。近年来，全光逻辑门的研究在国内也深受欢迎，2017年，刘天玮[8]基于SOA的交叉增益调制对全光信号处理技术中的全光波长转换以及全光逻辑门进行了理论和实验分析；2018年，胡永倩等[9]采用牛顿法和四阶龙格库塔法求解量子点半导体光放大器(Quantum Dot-Semiconductor Optical Amplifier，QD-SOA)的三能级跃迁速率方程和光场传输方程，讨论全光逻辑与门的转换效率和误码率；2019年，纪文珺等[10]设计了基于 SOA-MZI 的全光逻辑非门。以上文献的研究大多是基于SOA-MZI的研究，然而，与MZI相比，SI有诸多的优势，比如，不用考虑2个相干臂的臂长差，工程实现容易；不会将相位噪声转换为强度噪声；不存在偏振衰落现象等[11]。因此，基于SOA-SI的全光逻辑运算更易于工程实现。本文是从SOA和SI这2种器件的结合出发，研究基于SOA-SI结构的全光逻辑异或门及或非门。

1 理论模型

基于SOA-SI结构的全光逻辑门模型如图1所示。

WDM—波分复用器；C—环行器；IM—强度调制器；SL—半导体激光器；MLL—锁模激光器；SOA—半导体光放大器；PRS—伪随机序列。图1 基于Sagnac干涉仪逻辑门的系统模型

图1中，首先，锁模激光器(MLL)产生重复速率为10 Gb/s的时钟(CLK)信号A1，1个探测信号(弱信号)A1通过环行器(C1)并经过耦合器抵到Sagnac环中，形成顺时针Af和逆时针Ab信号。同时，另外2个半导体激光器(SL)产生连续的波信号分别以10 Gb/s的速率被2个不同的伪随机序列进行强度调制。这2个经过调制的波经放大得到泵浦信号B1和B2。然后，Af和B1通过波分复用器(WDM1)耦合到SOA1中，Ab和B2通过WDM4耦合到SOA2中。WDM2和WDM3用于分离从2个SOA中输出的泵浦信号。最后，2个被放大的信号A′f和A′b通过C3分别进入C4和C2再到达耦合器的第3和第4端口。基于SI的逻辑门依赖于Af和Ab之间耦合输出的切换。在某个SOA中，泵浦信号的功率很高即逻辑值为“1”时，许多的反向载流子将被耗尽；反之为“0”时，载流子将不会被消耗，并且它的受激辐射可以放大对应的探测信号，使探测信号获得高增益。

进一步的，针对系统模型进行理论分析，在SOA的有源区域中，材料增益因子取决于载流子的密度N。每单位长度的增益系数g(N)定义为：

gi(Ni)=dg/dN(Ni-Ntran)

(1)

式中，对于线性增益模型，微分增益dg/dN定义为gi(Ni)在Ni上的斜率，Ntran为透明点处的载流子密度。

使用Maxwell电磁方程组和密度矩阵方程，得到光信号沿SOA的传播时的表达式和载流子密度N(t)的动态速率方程[12]：

(2)

(3)

(4)

式中，i=1,2且P1和P2分别表示经过SOA1和SOA2的输出信号功率，Γ和αs为光的限制因子和波导的散射损失，g1和g2分别表示B1和B2各自波长的物质增益，pi,av为平均功率，I为进入有源区的注入电流，e为电子电荷，V=L×w×d为有源区的体积，其中L为有源区长度，w为有源区宽度，d为有源区厚度，f和h分别为频率和普朗克常数，s为非线性系数。在SOA中，Si,ASE为放大的自发辐射，通常被忽略。

根据式(3)，如果sPi,av≪1，可以在任何l(SOA的某个位置l)处获得功率：

(5)

所以，平均功率为：

(6)

式中，1-sPi,in+sPi,in=1。

在SOA中，载流子密度的变化导致非线性折射，通过调制信号相位，实现XPM。根据式(3)获得信号经过SOA的相位差：

(7)

式中，i=1，2且φout(1)和φout(2)分别表示经过SOA1和SOA2的输出信号相位，φin(1)和φin(2)分别表示进入SOA1和SOA2的输入信号相位，φ1和φ2分别表示信号经过SOA1和SOA2的相位差，α为线宽度增强因子。

信号B1和B2被2个SOA放大，放大后A′f和A′b在Sagnac干涉仪中满足：

(8)

式中，i为虚数单位，G1和G2为信号B1和B2经过SOA获得的增益，相移φ′1=φ1+βL′,φ′2=φ2+βL′,其中β，L′分别为波数和Sagnac环的长度。信号A′f和A′b通过耦合器耦合到T端口和R端口，耦合输出的结果为：

由于生产的智能工程机械设备，技术含量高，一旦设备发生故障，客户最看重的是厂家排除故障的速度。为此，山河智能在全国各地设立了20个售后服务网点，配备了100多台服务车。“过去高速公路路网不发达时，不敢承诺客户排除故障的时间。如今，高速公路路网发达了，公司承诺客户市内3小时之内排除故障，省内4小时内排除故障。”李伟伟说道。

(9)

(10)

Q因子广泛用于评估各种数字系统的性能，故用Q因子来表征逻辑输出信号的品质，计算公式如下：

(11)

输出逻辑值判定为“1”和“0”时，平均功率分别为〈P1〉和〈P0〉，标准差分别表示为〈σ1〉和〈σ0〉。Q以 dB为单位时，QdB=10×lgQ，在高斯分布逼近下，系统中的Q和比特误码率(Bit Error Ratio，BER)之间的关系为：

(12)

另外，输入的泵浦信号波形为：

(13)

式中，an为第n个符号(为0或1)，nT0表示第n个脉冲的时间位置，σ为信号的半高全宽。

2 数值模拟与分析

数值模拟实验先使用龙格-库塔法对方程(2)—(4)进行数值求解，分析泵浦功率对载流子密度和增益的影响，再结合耦合矩阵(8)—(9)来分析T和R端口实现的逻辑功能，仿真模拟在MATLAB中实现。模拟中，假定信号传输的比特率为10 Gb/s，仿真参数如表1所示。

表1 数值模拟中主要参数

2.1 泵浦功率对载流子的密度和增益的影响

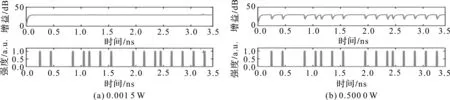
图2 泵浦功率对载流子密度和增益的影响

2.2 异或门、或非门的实现

取B1和B2波长为1 555 nm，峰值功率为0.5 W，将其作控制信号以分别实现Af和Ab的XGM和XPM。设A1波长为1 550 nm，其峰值功率为1.5 μW。令分光比ρ=0.5。用四阶龙格-库塔法求解式(2)—(4)，并使用耦合矩阵式(8)和式(9)求得SI的T和R端口的输出，输入、输出的关系及眼图状态分别如图3和图4所示，“眼睛”张开大小表示失真的程度，用于衡量眼图的质量。

图3 Sagnac干涉仪T端口的XOR逻辑输出

从图3可以看出，眼图完全打开，表明在T端口生成的逻辑信号具有很高的逻辑正确性和品质，实现了XOR门。T端口输出信号的ER高达14.47 dB，结合式(11)得Q因子达到7.57(以dB为单位，Q因子为8.79 dB)，BER低至1.8210-14。

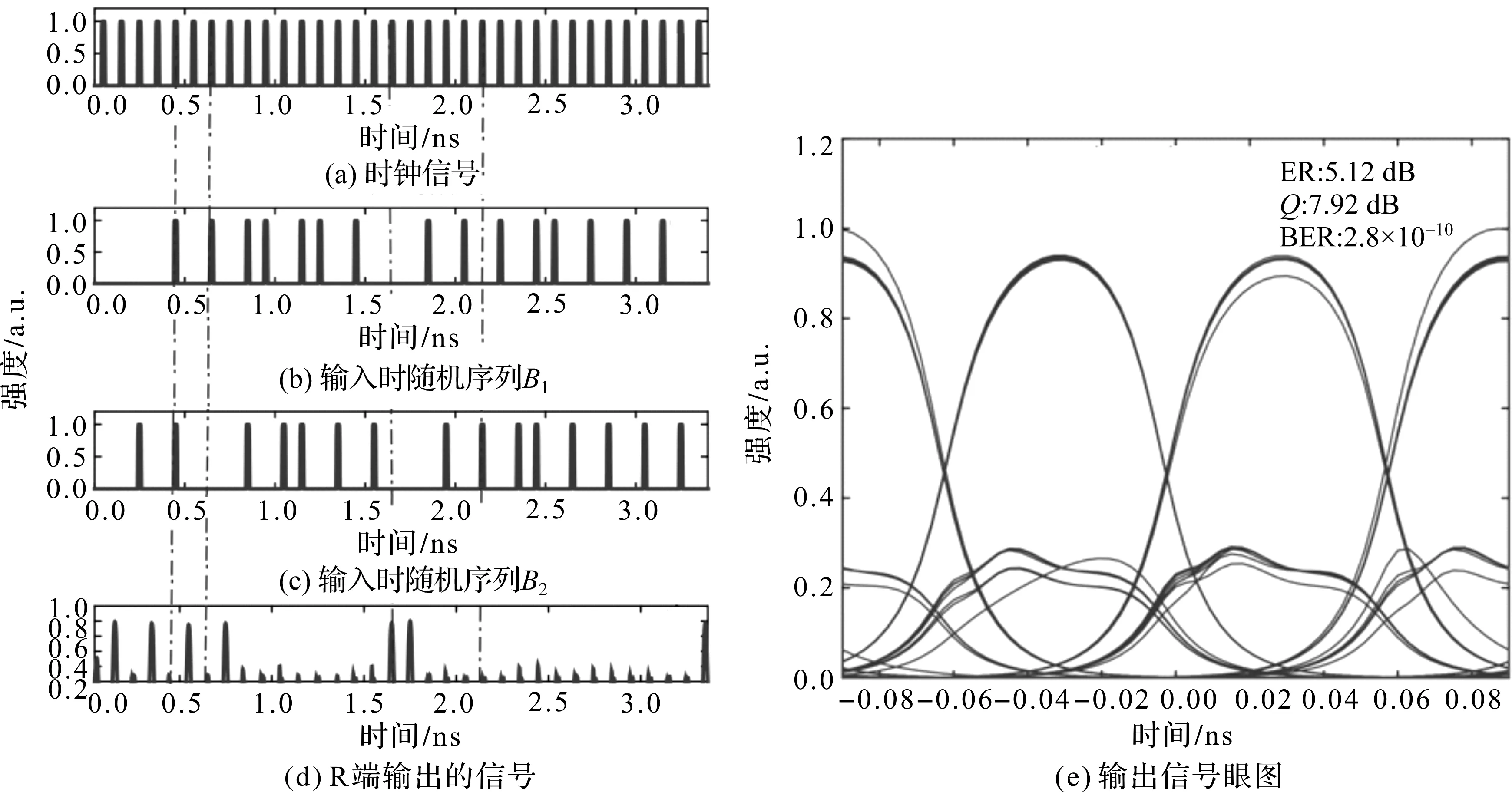
图4 Sagnac干涉仪R端口的逻辑输出

从图4可以看出， R端口实现了NOR门，其ER高至5.12 dB，Q系数达到6.20(以dB为单位，Q因子为7.92 dB)，BER为2.8010-10。同时眼图具有良好的张开度。将这些参数与图3的相比，信号的品质明显差一些，但逻辑值“1”或“0”的判断不受影响。图4(e)的眼图比图3(e)上眼皮要光滑，它们的不对称是由于SOA中载流子的变化与泵浦光功率变化之间是非线性的，泵浦光从1到0的下降段，和从0到1的上升段，对应增益的上升和下降时间会不同。图4(e)的对称性好，其上眼皮对应泵浦为(0,0)组合，泵浦功率都为0，而图3(e)上眼皮对应(1,0)和(0,1)组合，只有一个SOA有泵浦光。图4(e)眼图对应的泵浦为(0,0)，不消耗载流子，图3(e)眼图对应(1,0)和(0,1)组合只有一个SOA中的载流子消耗，这样消耗载流子时，一个非线性饱和，另外一个处于线性放大，导致图3(e)眼图变化的起伏更大，对称性差。

上述计算和分析表明，信号传输的比特率为10 Gb/s时，本文得到的信号品质较优，在实现异或门的Q因子的值7.570没有比文献[10]实现非门的Q因子的值7.288低的情况下，和文献[10]比特率为1 Gb/s处于最好效果相比，本文的传输的速率更快，且本文一次输入获取2个逻辑门，使获得的逻辑门效率更高。

图3、图4中，虚线对应的4种情况表示通过输入信号(0,0)，(0,1)，(1,0)，(1,1)的4种组合分别得到的输出逻辑值，根据逻辑输入和输出之间的状态绘制相应的逻辑功能，结果如表2所示。

表2 输入与输出逻辑关系实现的逻辑门

3 结束语

本文使用四阶龙格-库塔法方法求解SOA的速率方程，通过改变SOA的输入电流、微分增益得到最佳的反转载流子，利用泵浦信号控制SOA中的载流子密度的消耗程度，实现探测信号的XGM和XPM，并结合SI的耦合性实现了XOR门、NOR门。研究表明，SOA-SI模型可得到不同的逻辑功能，并获得较高的逻辑门效率。在以后的实验研究中，将进一步结合模型实现其他逻辑功能。