无线供电用植入式集成线圈建模

石昊云，程瑜华，王高峰

(杭州电子科技大学电子信息工程学院，浙江 杭州 310018)

0 引 言

植入式心脏起搏器、人工耳蜗、神经刺激器等植入式医疗器件已得到广泛的应用。为减小植入式器件对人体的侵入性，器件的尺寸越小越好。采用无线供电来避免电池植入是减小植入器件尺寸的重要手段之一。在基于磁场耦合、电场耦合、超声耦合等多种耦合方式的无线供电技术中，通过体内外线圈间的磁场耦合进行无线供电是当前最为成熟的技术。电能的传输效率是无线供电系统最受关注的参数之一，效率越高意味着在相同的发射能量下，人体组织吸收越少的能量。线圈间的能量耦合效率取决于线圈间的耦合系数和线圈的品质因素[1]，而这些参数由线圈的结构、尺寸和线圈周围的环境(如介电常数、磁导率等)决定，因此，有必要对线圈进行设计优化。若能给出线圈物理尺寸与线圈自感、品质因素之间的电学模型，则可根据设计目标(比如最大化品质因素)进行快速优化，再使用电磁场仿真工具进行验证。文献[2]采用纯数学解析的方式计算介质环境的寄生电容影响，但是当介质环境复杂时就不再适用。在此基础上，本文采用多层介质叠加与拟合的方式，对植入体内的集成线圈在生物兼容材料和人体组织包裹下的寄生电容进行准确建模和仿真验证。

1 植入式硅基集成线圈模型

图1 硅基集成线圈的示意图及集总参数模型

植入式硅基集成线圈的模型示意图如图1(a)所示，集总参数模型如图1(b)所示。线圈总阻抗Z和Q值的表达式如下：

(1)

Q=lm(Z)/Re(Z)

(2)

式中，LS为电感值，RS为串联寄生电阻，CP为并联寄生电容，GP为并联寄生电阻RP的倒数，ω为工作角频率，j表示虚部部分，Im(Z)和Re(Z)分别为线圈阻抗Z的实部和虚部。从式(1)和式(2)可知，准确的寄生参数是优化线圈品质因素Q值及寻找最佳工作频率的基础。

1.1 自电感与寄生电阻模型

参考文献[3]得出平面螺旋线圈的电感表达式为：

(3)

式中，系数ci(i=1,2,3,4)值由线圈的形状决定，如八边形线圈分别取1.09，2.23，0.00，0.17[3]；μ为线圈环境的磁导率，且μ=μrμ0，μr和μ0分别为相对磁导率和真空磁导率；n为线圈匝数；davg=(din+dout)/2，din和dout分别为线圈的内径和外径；ρ=(din-dout)/(din+dout)是填充因子。式(3)的误差在线间隙与线宽比值超过3时误差达到8%。单匝线圈中，寄生电阻RS主要由趋肤效应决定。趋肤效应指金属导体在高频电流通过的情况下，电流往导体表面集中并导致电阻增加的现象。等效电阻RS为[4]：

(4)

式中，RDC为直流电阻，t及w为导体厚度和宽度，δ为趋肤深度。

1.2 寄生电容模型

1.2.1 空气中寄生电容C0

对于处于空气中的线圈的寄生电容的研究，文献[6]认为由多匝线圈间相邻匝的线圈导体之间形成的平板电容大小决定，并用平板电容器的计算公式计算，文献[5]和文献[2]将线圈看成共面传输线，利用保形映射(Conformal Mapping)和施瓦茨变换(Schwartz Transformations)进行计算。然而，这些计算并不适用于单匝线圈的情况。对于处于空气中且没有衬底的单匝线圈，其寄生电容C0可以由自谐振频率和自感值反推得到。此时的自谐振频率可以认为是传输线谐振，即线圈长度是自谐振频率对应的波长的1/2或1/4(分别对应线圈开路或短路时)，进一步考虑到负载的影响，线圈在自由空间中的自谐振频率如下：

f0,ST=kFc/2l

(5)

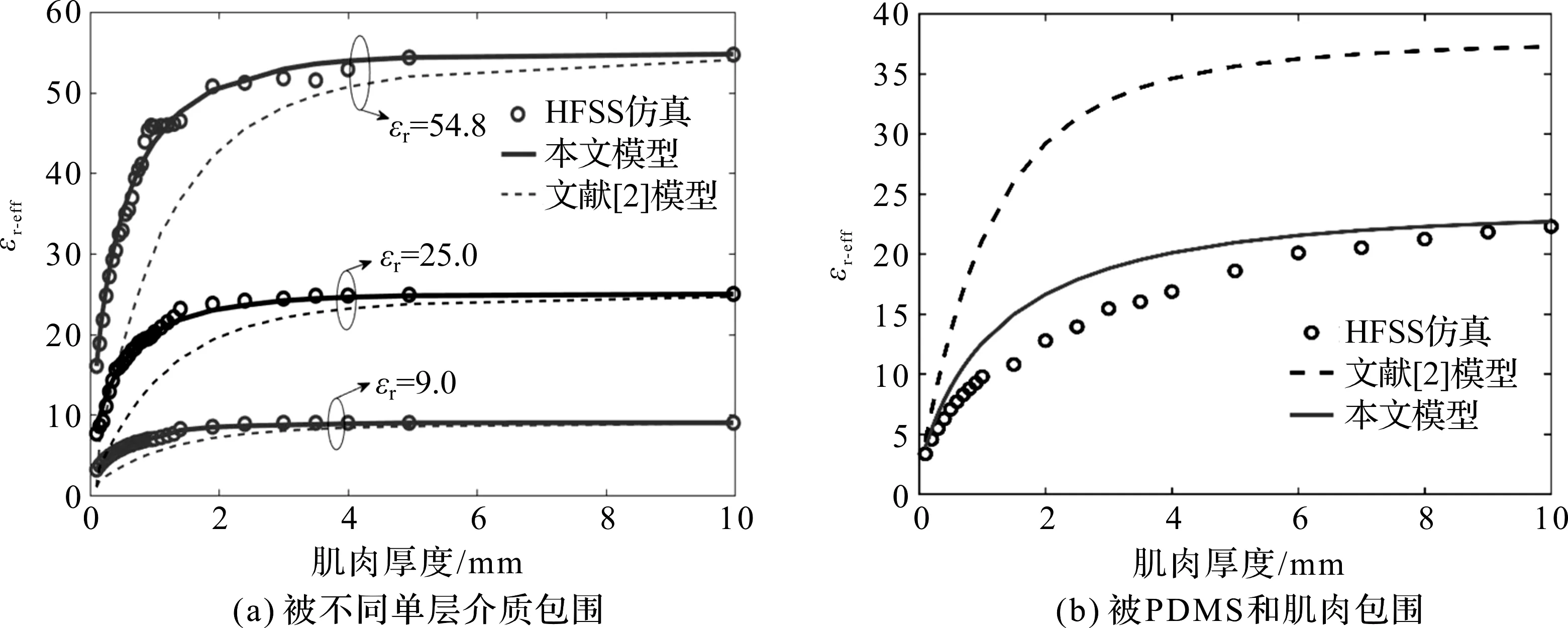
式中，c为真空中电磁波的传播速度，l为线圈长度，kF取决于负载(0.5

C0=1/(2πf0,ST)2LS

(6)

多层介质环境导致寄生电容的模型较为复杂，为更好地表示线圈的介质模型，本文将其简化为图2(a)所示的结构，线圈基板介质是硅，在制造过程中，硅上方出现一层极薄的二氧化硅，图中包裹线圈的生物兼容性材料为PDMS，在PDMS外是人体组织层(以肌肉为例)，图中标注了各种介质材料的介电常数。

当线圈周围为单一介质环境时寄生电容容易获得，因此，将线圈周围的多层环境介质简化成多个单一的介质叠加环境可以将建模过程简化。此外，线圈上方和线圈下方的介质环境不同，如图2(b)所示。将上方和下方的介质分开分析可以简化建模过程，相应的总寄生电容CP可由上方电容和下方电容并联组成。

图2 植入式硅基集成线圈的简化模型及线圈上方介质环境的示意图

(7)

式中，介质的厚度单位为μm，a与b为拟合系数。

图3 多层介质分解为多个单层介质示意图

(8)

式中，t1，t2，t3-up，t3-down，t4-up,t4-down分别为硅衬底厚度、二氧化硅厚度、PDMS在线圈上方的厚度、PDMS在线圈下方的厚度、肌肉层在线圈上方的厚度、肌肉层在线圈下方的厚度。

(9)

1.2.3 介质损耗RP

(10)

2 仿真实验与结果分析

根据1.2.2节所述，将多层介质简化成多个单层介质的叠加，再通过单层介质的等效介电常数拟合得到硅基集成线圈的等效介电常数模型，并使用电磁场仿真工具HFSS进行仿真。

线圈如图1(a)所示的八边形结构，外径do=4.00 mm，线宽w=0.25 mm，厚度t=25 μm，线圈所用材料为金。线圈被一定厚度的一种介质包围，并且整体再被空气包围时的等效介电常数随此介质厚度和介电常数变化的HFSS仿真和模型计算结果如图4(a)所示，图中分别采用式(8)寄生电容模型和文献[2]解析计算模型进行等效相对介电常数对比。从图4(a)中可以看出，本文模型计算结果与仿真结果很接近，且精度明显高于文献[2]模型。线圈被PDMS和肌肉包围，并且整体再被空气包围时的等效相对介电常数在0.5 mm厚的PDMS和不同肌肉组织厚度条件下的计算和仿真结果如图4(b)所示。从图4(b)可以看出，虽然本文模型与仿真结果有一定的误差，但是，本文模型的精度依然高于文献[2]模型。

图4 线圈被单层介质和双层介质包围，再被空气包围时的等效介电常数

在如图2(a)所示更多层介质包围下，线圈的阻抗和品质因数的仿真结果如图5所示。其中，线圈被电镀到25 μm厚的硅基上，产生50 nm厚的二氧化硅，再被0.5 mm厚的PDMS包裹后插入到20 mm厚的肌肉正中间。

图5 肌肉厚度为10 mm，PDMS厚度为0.5 mm时的仿真结果

如图5(a)所示，本文电容模型比文献[2]模型更接近于仿真结果，而电阻和电感模型与文献[2]相同，但由于阻抗实部的计算也受寄生电容的些许影响，导致图5(b)中本文模型和文献[2]的阻抗实部结果略微不同。图5(c)中，文献[2]模型计算的电容值更大，使Q值最大值对应的频率更早出现在0.60 GHz左右，而本文模型与仿真结果的Q值最大值对应的频率均出现在0.84 GHz左右。相对而言，本文模型提高了最大Q值对应频率的精度。

在无线电能传输中，为提高传输效率，通常将工作频率设置在线圈Q值最大处，因此Q值最大值对应的频率fQmax在实际应用中具有重要价值。在不同肌肉厚度下，本文模型和文献[2]模型计算得到的fQmax值如图6所示。

图6 不同肌肉厚度下，fQmax对比

从图6可以看出，本文模型虽与仿真结果仍然存在一定误差，但是其精度相比文献[2]模型有很大的提高。尤其在肌肉厚度6 mm以上时(即植入式器件应用的典型场景)，模型与仿真之间的误差在5%以内。

3 结束语

本文对植入式硅基集成线圈在多层介质包围下的电学特性进行解析和建模。尤其在电容的建模上，通过将多层介质简化为多个单层介质的叠加，再用单层介质情形的等效介电常数进行精确拟合，提高了电容模型的精度，从而提高了线圈阻抗和品质因素的计算精度，可以更有效地计算线圈的最佳工作频率。后期将对线圈的损耗模型展开研究，使得线圈的品质因素与仿真和实验结果更吻合。