网络分析仪时域测量技术综述

张 娜

（北京无线电计量测试研究所，北京100039）

1 引 言

矢量网络分析仪采用比值测量模式描述二端口网络的传输特性和反射特性，是目前微波测量领域中应用最广泛的仪器之一。 网络分析仪最常用的是频域测量模式，描述被测件的频率响应。 在进行失配网络的不连续性测试时，矢量网络分析仪的时域技术可以直接显示被测件的时间（距离）响应，从而确定不连续点的位置和幅度等信息。

网络分析仪是基于频域进行测量的，时域技术是基于傅立叶变换（FFT）进行的纯数学计算过程［1］。 网络分析仪时域测量与直接傅立叶逆变换（IFFT）有所区别，这是因为网络分析仪时域测量时添加了各种限制（如频率范围）和补偿。 矢量网络分析仪测量的时域变换在1974年被首次提出［2］，于1984年嵌入矢量网络分析仪HP8510A 成为商用版本，近年来时域测量已成为矢量网络分析仪的一个基本功能选项。 国内外网络分析仪主要制造商如美国Keysight 公司、德国R＆S 公司、日本Anritsu公司和中国41 所推出的一系列矢量网络分析仪都配备了时域选项。 网络分析仪时域选项提供了多种测量模式和窗口形状，结合时域门技术能够有效消除干扰信号的影响，提高测量结果的精度和指标，但是测量模式和测量参数的选择将影响测量结果，因此理解时域测量原理，合理设置时域测量参数对保证测量结果的准确度有着重要意义。

本文对传统傅立叶变换（FFT）理论不做介绍，从测量角度出发主要介绍网络分析仪时域测量的相关技术。 采用美国keysight 公司矢量网络分析仪N5225A、美国keysight 公司2.4mm 同轴校准箱85056A 进行实验，首先完成网络分析仪的单端口校准，分别测量开路器的频域响应和时域响应，分析和理解网络分析仪时域测量参数的影响。

2 时域测量

2.1 时域测量模式

时域反射测量技术（TDR）常用于被测器件的时域分析，传统时域反射计是将冲击信号或阶跃信号发送至被测器件，采用示波器观测信号的时域响应。 由于示波器具有宽带接收的特点，其信噪比较差。 矢量网络分析仪时域测量不同于传统时域反射计，它是将被测器件的频域响应进行傅立叶逆变换得到时域响应。

网络分析仪提供时域低通冲击模式（Low Pass Impulse）、时域低通阶跃模式（Low Pass Step）和时域带通模式（Band pass）三种测量模式。 矢量网络分析仪默认为时域带通模式。 时域带通模式适用于任意频率范围的测量，它是将频率测量数据直接进行傅立叶逆变换。 时域低通冲击模式和时域低通阶跃模式要求终止频率必须等于起始频率与测量点数的乘积，网络分析仪可自动完成该项设置。 低通模式中参与傅立叶逆变换的数据包括频域测量数据、外推直流值和与正频率响应共轭的负频率响应。 低通模式中参与傅立叶逆变换的数据是带通模式的两倍，因此对相同的测量频率跨度和相同测量点数来说，低通模式冲击宽度是带通模式冲击宽度的二分之一，具有更高的分辨率。 设计实验为在10MHz ～50GHz 频率范围测量不同时域模式时开路器的时域响应，不同时域测量模式的数据对比见表1。

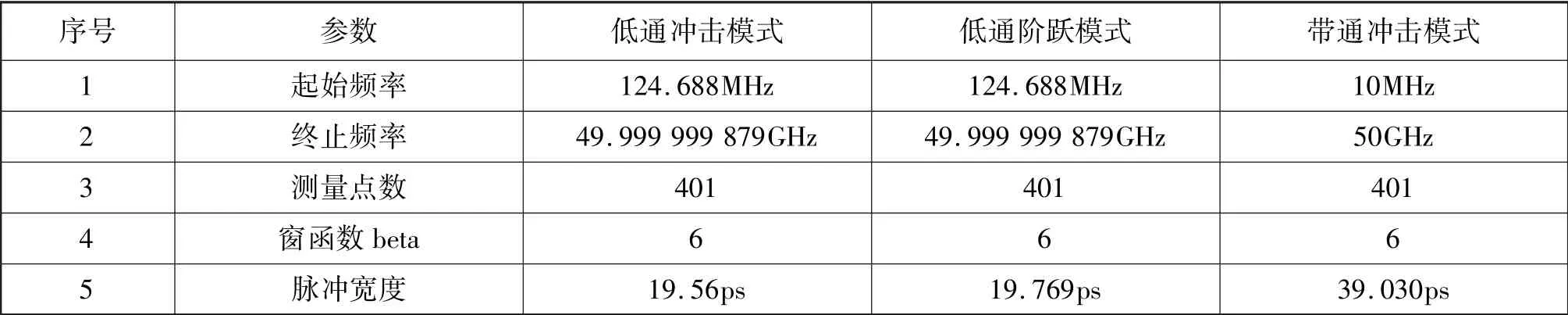
表1 开路器时域测量模式比较Tab.1 Time domain model of open

2.2 时域测量理论

矢量网络分析仪进行时域测量时添加了各种限制（如频率范围）和补偿，这使得矢量网络分析仪的时域响应与基于傅立叶逆变换得到的理论计算结果不完全相同［3］，下面将详细分析离散数据取样、频率截断、窗函数和归一化等因素的影响。

2.2.1 离散数据取样

众所周知网络分析仪测得的频域响应是离散数据，而傅立叶变换是基于连续函数的，因此通常需要假定网络分析仪测量数据为连续函数的采样，再进行傅立叶逆变换处理。 离散数据采样的一贯性将产生一系列等间隔的原函数镜像，称为假象，假象间隔为频率步长的倒数1／Δf。 进行时域测量时，首先根据被测件的时域关注范围，来设置测量频率跨度和测量点数，使得时域响应出现在假象之前。假象可以通过如下方法区别：改变测量点数，观测时域响应，实际响应不变，发生变化的响应为假象。

设计实验为在10MHz ～50GHz 频率范围测量开路器的时域响应，如图1所示。 当改变测量点数时，实际响应（0s）的幅度和位置未发生变化，而假象发生了幅度变化，时域假象间隔分别为1／50GHz／400 ＝8ns 和1／50GHz／800 ＝16ns。

图1 不同测量点数离散采样得到的时域响应曲线图Fig.1 Time domain response of different numbers

2.2.2 频率截断

矢量网络分析仪的频率测量范围是有限的，因此频域响应可认为是一个无穷大范围的频域响应与矩形窗函数的乘积，数据样本被截断。 矩形窗函数的逆变换为sinx／x［4］，则网络分析仪测量结果的时域响应即为网络的时域响应与函数sinx／x 的卷积，因此矩形窗函数使得网络分析仪的时域响应产生了旁瓣，如图2所示。

2.2.3 窗函数

由数据截断产生的旁瓣有时很大，将掩盖被测器件的真实响应。 因此通常对频域测量数据进行加窗函数处理。 常用的窗函数是凯塞－贝塞尔窗（kasiser-Bessel），如图3所示。 图3（a）给出了增加窗函数（beta ＝13）后开路器的时域响应，与图2 相比旁瓣电平明显下降。

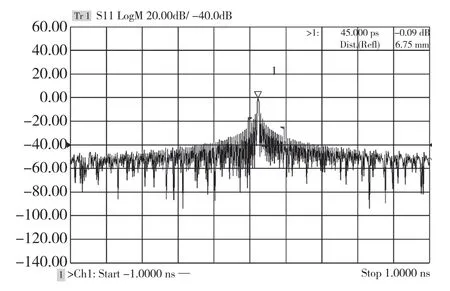
图2 频率截断产生的旁瓣效应曲线图Fig.2 Nearby response of frequency truncation

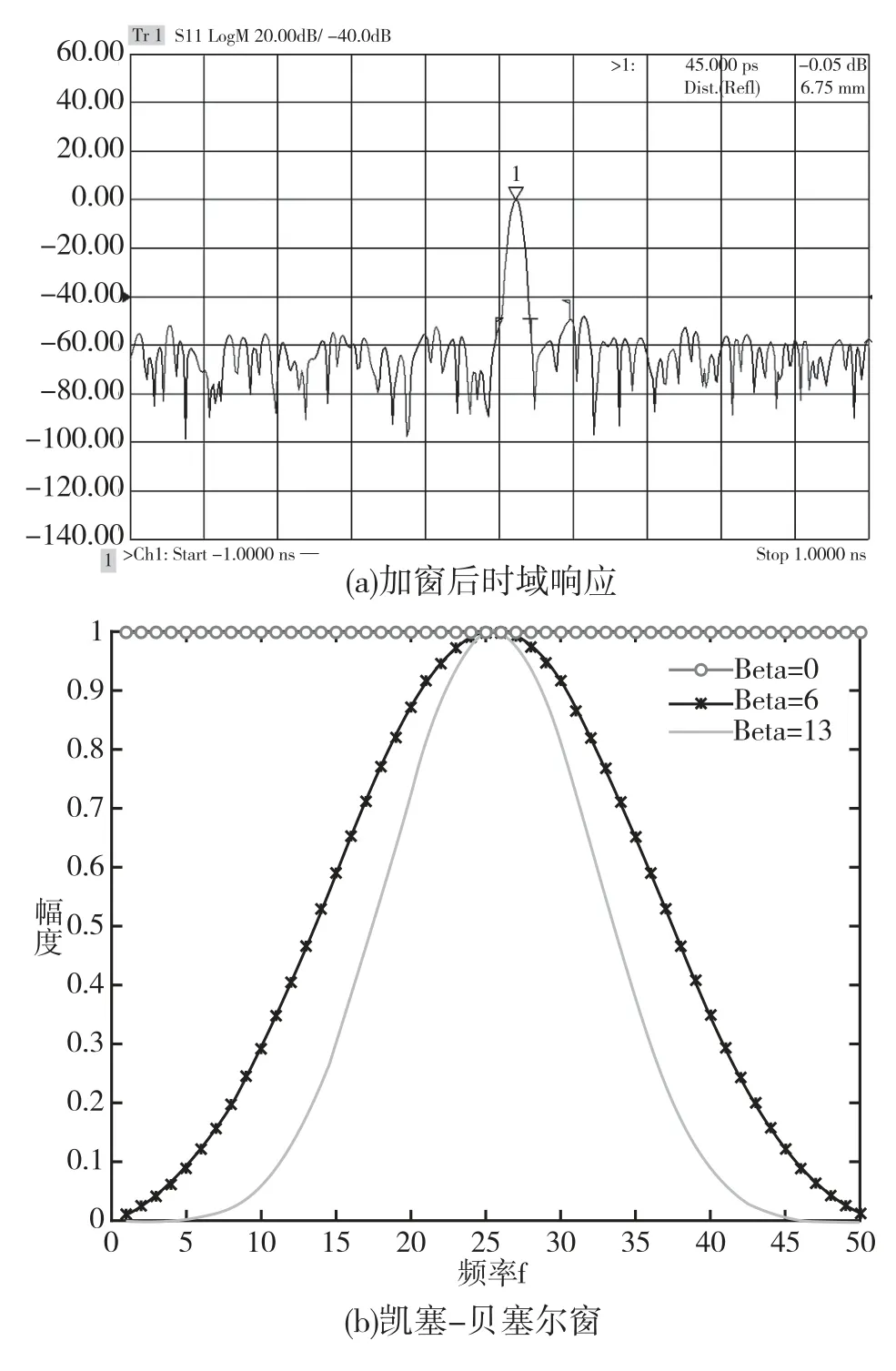
图3 加窗后响应曲线图Fig.3 Response with window function

矢量网络分析仪中窗函数的设置主要有beta参数，图3（b）给出了beta 参数分别为0，6，13 时凯塞－贝塞尔窗函数的形状。 窗函数有带内波动、冲击宽度等特性指标，可通过beta 值调节窗函数的特性指标［5，6］。 beta 值越大，窗函数越窄，带内波 动小，对旁瓣的抑制效果越好，相反，beta 值越小，窗函数越宽，带内波动大，对旁瓣的抑制效果越差。 当窗函数变窄，冲击函数宽度或阶跃函数上升沿变宽，将展宽冲击宽度，降低分辨率，见表2，因此网络分析仪设置窗函数时应该综合考虑旁瓣和分辨率的因素。

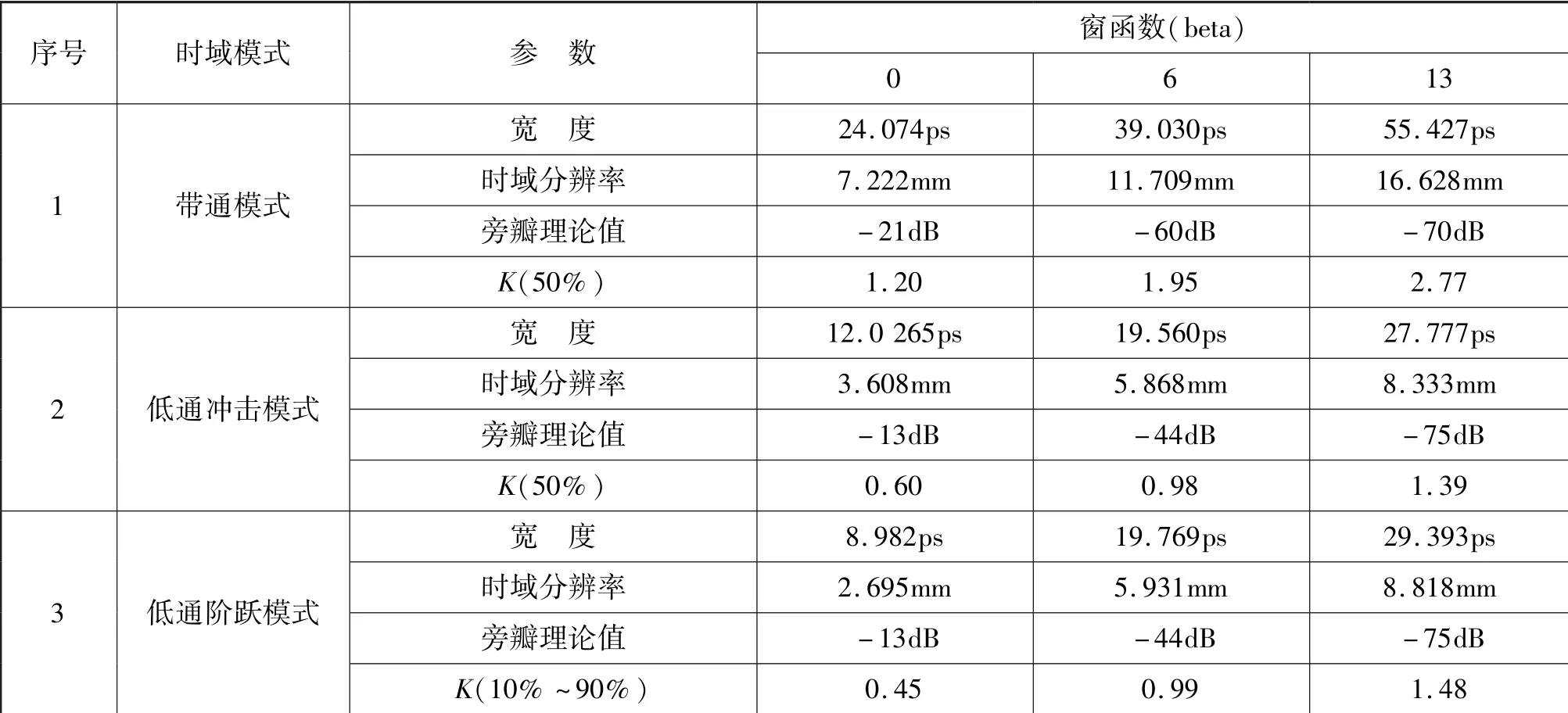
表2 时域响应分辨率Tab.2 Resolution of time domain

2.2.4 归一化

由于频域数据的窗函数处理使得时域响应被展宽而发生时域幅度失真，需要对时域变换数据进行再归一化处理以保持其物理意义［7］。 设计实验在10MHz ～50GHz 频率范围对网络分析仪进行单端口校准，然后接入校准开路器，理想情况下校准开路器的频域响应为1。 当观察开路器的时域响应时，由于数据被加窗处理，时域响应被窗函数展宽，幅度不为1，因此必须进行再归一化处理，保证开路器的理想全反射特性。

2.3 时域测量参数

网络分析仪频域响应转换到时域响应后，横轴是时间（距离），纵轴是幅度，因此时域中两个重要参数是测量范围和分辨率。 时域测量范围决定着能否将被测件的时域响应全部显示，时域分辨率决定着两个相邻响应能否分辨出来的能力。

时域测量范围可通过下式进行估计，它与频域分辨率、传播介质等相关。 当被测器件确定后，时域测量范围仅与频率分辨率成反比，因此可通过增加点数或减小频率跨度的方法来拓宽时域测量范围。 网络分析仪进行时域测量时需要根据时域需要的显示范围估计频域的测量范围和测量点数。

式中：T——时域测量范围，单位为米，m；Δf——频域分辨率，单位为赫兹，Hz；c——光速，3E8m／s；ε——被测件填充介质的相对介电常数。

时域响应分辨的最近程度称为时域分辨率，时域分辨率与时域模式、频率跨度、窗函数形式等有关。 时域分辨率等于冲击宽度乘以光速，而冲击宽度等于K［8］除以频率跨度

式中：ΔT——时域分辨率，单位为米，m；f——频域测量范围，单位为赫兹。

3 结束语

本文对网络分析仪时域测量技术进行介绍，首先介绍了时域低通冲击模式、时域低通阶跃模式和时域带通模式三种模式，接着分析了离散数据取样、频率截断、窗函数、归一化等对时域变换引入的影响，给出了时域测量范围和时域分辨率的计算方法。 以10MHz ～50GHz 频率范围开路器的时域响应为例，详细说明了在时域响应测量时，要根据被测器件的长度选择所需要的时域测量范围，根据所需分辨的最小距离确定时域分辨力，从而确定频率跨度、测量点数、测量模式及窗函数形式等获取时域响应。