空间计量与脉冲星导航

2019-03-25 02:35刘志宏

宇航计测技术 2019年1期

刘民帅平刘志宏李军

（1.北京东方计量测试研究所，北京100086；2.中国空间技术研究院钱学森实验室，北京100094）

1 引言

脉冲星是高速自转的中子星，其磁极轴与自转轴有一个固定的夹角，两磁极沿轴线方向连续辐射出宽谱段电磁波，从射频到γ 射线频段均有能量分布，随着脉冲星的自转，辐射能量周期性地扫过太阳系，太阳系各处都能探测到周期性的脉冲信号。脉冲星距离太阳系非常遥远，因此相对于太阳系惯性框架，它几乎静止不动，每颗脉冲星有自己独特的脉冲轮廓，周期非常稳定。据加拿大McGill 大学、英国Manchester 大学、美国Columbia 大学、Cornell 大学以及德国、荷兰等学者联合发布的论文，对最新观测的5 颗毫秒脉冲星的观测数据进行计算，得出周期变化率在10－19～10－21s／s 之间［1］。目前已编目的脉冲星有2000 多颗，可适用于导航的X 射线脉冲星达到几十颗，长期计时稳定度优于10－15／d［2］。脉冲星以其超高稳定性将成为太阳系内时空守时系统的自然基准。当脉冲星在惯性坐标系中的固定位置、脉冲周期以及脉冲轮廓成为已知量时，携带脉冲星探测设备的航天器就可以利用这些信息进行自主导航，并且具备了时间计量能力。脉冲星导航的基本原理，见图1。脉冲星的电磁辐射进入太阳系内可看作平面电磁波，先不考虑光线在引力场中的弯曲，简单理解为一对平行光线从脉冲星方向到坐标原点OSSB和航天器，脉冲星PSR1 的某一个脉冲信号到达OSSB的时间为tSSB1，同一个脉冲信号到达航天器的时间为tSC1，时间差△t1＝tSSB1－tSC1＝d1／c，其中c 为光速常数。 tSC1为航天器用原子钟观测，经运算处理后的测量值。 tSSB1为已知量，是地面长期观测PSR1 的数据，经处理生成的星历表中该脉冲预期到达OSSB点的时间。那么在PSR1 视向方向航天器到坐标原点的距离d1就可以计算出来。同理，获得至少在三个不同方向上航天器到原点的距离后就可以利用几何关系确定航天器在坐标系中的具体位置，通过星历表时间还可对航天器的时间测量系统进行校准。

图1 脉冲星导航原理示意图Fig.1 The principle of Pulsars navigation

上述过程看似简单，但存在着坐标系选择，时间单位的统一，多普勒效应［3］，以及在大尺度广域时空中建立守时系统等空间计量问题。空间计量理论将广义相对论与传统计量理论相结合，解决地球以外更广阔的宇宙空间的测量单位统一和测量准确的问题，要求我们站在四维时空的角度理解物质的存在和运动规律［4，5］。该理论认为时间和长度的计量单位是绝对定义的，不随坐标系的不同而改变，同时性仅在同一个坐标系中有定义，不同坐标系之间不能直接进行时间比对，时间统一和时间单位的统一是相互矛盾的，建立时间和空间统一的方法有两种，当前地球卫星导航系统（GNSS）只是其中之一［6］，脉冲星导航将用到另一种方法。文献［2］系统地介绍了脉冲星导航的理论和计算，本文从空间计量角度来理解，提出建立大尺度广域时空中建立守时系统的设想。

2 脉冲星导航的坐标系选择

描述宇宙时空，依赖坐标框架，参考点和参考方向决定了坐标框架的性质，在坐标框架中，若确定了具体的参考点、方向和坐标轴的刻度规则，就可以确定一个具体的坐标系，于是航天器在时空中的运动规律就可以用数学公式来精确表达。一种坐标框架中可以定义几种不同的坐标系，例如，在惯性坐标框架中可以定义太阳质心坐标系、太阳系质心坐标系、地心惯性坐标系等等。如以太阳系质心OSSB为参考点，当春分时刻OSSB与地心连线的方向为X 轴，以黄道面法线方向为Z 轴，用右手法则确定Y 轴，用黎曼空间的度规确定坐标刻度关系，定义时间起始点（也称初始历元），就可以定义太阳系质心坐标系。同一个坐标框架中的各种坐标系可以进行相互转换，把坐标、速度、姿态角、时间等参数通过坐标系之间的关系进行相互转换。但是不同坐标框架之间的数学转换非常复杂，星际导航一般不使用非惯性坐标框架。

空间计量的一个原则是“仅在同一个坐标系中具有同时性”，就是说，不同的坐标系之间不能直接进行时间的比较和传递，脉冲星、航天器、地球和太阳有各自的坐标系，它们之间不能直接比对时间。站在地心惯性坐标系和太阳系质心坐标系上观测同一个脉冲星的脉冲到达时间（TOA）的间隔是不同的。对于同一个地球轨道航天器上的观者，他既在太阳质心坐标系中，又在地球质心坐标系中，用同一个原子钟，用SI 秒为单位，记录了脉冲星的两次TOA，虽然原子钟的读数是客观且唯一的，但是经过时间尺度坐标转换之后，TOA 的间隔表现在不同坐标系中就不相同，这也被称为时间尺度转换。为便于理解，简单忽略了c－3及更高次小量，简单化的转换公式如式（1）

式中：Δt——转换到太阳质心坐标或地球质心坐标的一段时间，单位SI 秒；τ——航天器原子钟的读数，单位SI 秒；U——航天器在测量τ 时刻所处的引力势，含太阳和地球共同作用，有周期变化分量；V——若在太阳质心系中是相对于原点的线速度，有周期变化分量；若在地球质心系中是相对于地心的线速度，在圆轨道上无周期变化；c——光速常数。

同样使用式（1），代入相对于不同参考点的线速度V，所算得的时间间隔是不同的。其原因是两个坐标系中时间坐标轴的刻度规则（度规）不同，不论是太阳系质心坐标系，还是地心惯性坐标系，在时间坐标轴都是弯曲的，即时间坐标轴的度规g00不是常数，而是与引力势和相对速度相关的变量。

脉冲星自身特有的脉冲轮廓是区别不同脉冲星信号的特征之一，是准确计算脉冲到达时间钥匙，将轮廓上最具特征的曲线拐点定义为脉冲到达时刻点，如轮廓的峰尖，当标准脉冲轮廓与实时测量的脉冲轮廓重叠时，记录一次脉冲到达时间。脉冲星X 射线光子能量很微弱，同一个方向上还有许多其他脉冲星同时提供光子能量，不能直接绘出某颗脉冲星入射X 射线光子能量随时间变化的曲线，需要将连续多个周期上相同相位的光子能量叠加起来才能有清晰的轮廓，这称为脉冲轮廓折叠。假设原子钟的时间坐标刻度是均匀的，脉冲星的每个脉冲相对于航天器来说也是均匀到达的，以脉冲周期为间隔来进行折叠，把各周期上具有相同相位的光子能量叠加，就得到标准脉冲轮廓。然而实际上这种假设不成立，首先航天器原子钟的走速仅在自身所处的局域坐标系上是均匀的，其所记录的时间间隔转换到其他坐标系上就不再均匀了，考虑引力红移和相对速度的影响，从地球质心坐标系上看圆轨道航天器，时钟走速有一个固定偏移，从太阳质心坐标系上看绕地球旋转的航天器，时钟走速有时快，有时慢，呈周期性变化；其次脉冲星的脉冲也不是均匀到达航天器的，受多普勒速度效应影响，航天器朝着脉冲星方向运动时，所测量的脉冲间隔短，背着脉冲星方向运动时，间隔长。

S.Sheikh（2005）利用NASA 公布的ARGOS 卫星轨道参数和所记录的Crab 脉冲星（PSR B0531 ＋21）数据获得了如图2所示的脉冲轮廓［7］。其中，图2（a）是长期高精度时间尺度转换获得的标准脉冲轮廓，图2（b）是卫星原子钟的时间坐标轴上相同相位测得的光子数叠加获得的脉冲轮廓，相比标准脉冲轮廓，其尖峰很不清晰，其原因是受到相对论效应的影响卫星原子钟的走速相对于脉冲间隔是不均匀的。在速度变化不大的情况下，连续的相邻周期上的轮廓受多普勒效应影响并不明显。图2（c）是将卫星位置近似于地球质心，用地球在太阳轨道上的引力势和相对速度参数进行了时间尺度转换，再把转换后时间坐标轴上相邻周期同相位所测光子数叠加获得的轮廓，其尖峰已经较为清晰。图2（d）是考虑卫星在太阳系质心坐标系中受到的相对论效应，用卫星在地球和太阳轨道上的引力势和相对速度参数进行时间尺度转换，再进行脉冲轮廓折叠，其尖峰更为清晰。这说只有用太阳系质心坐标系来测量脉冲间隔才能获得准确结果，而地心惯性坐标系和卫星局域坐标系与脉冲星不在相同坐标系中，因而不能进行直接的时间比对，不具备同时性条件。这也说明，只有站在太阳系质心原点OSSB上看脉冲星，是静止的，脉冲星和OSSB处于相同的坐标系上，具有同时性。而航天器和地球质心对于脉冲星来说，是相对运动的，不在同一个坐标系上，不能直接比对时间。图2（e）是卫星相对于脉冲星速度－4.8km／s 和0.13km／s 两个时段，在原子钟的时间坐标轴上直接进行脉冲轮廓折叠的结果，轮廓几乎无法分辨尖峰，如果认为脉冲星的周期和轮廓是稳定的，那么多普勒效应的影响是对时间坐标轴刻度的影响。当速度变化缓慢时，可以采用伸缩时间坐标轴比例的方法来修正多普勒效应。

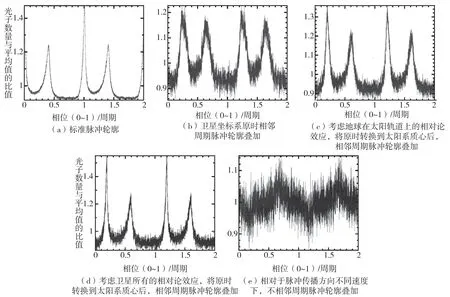
图2 Crab 脉冲星的脉冲轮廓在不同坐标系的时间轴上的周期叠加波形图Fig.2 The pulse profile of Crab PRS folded on time axis of different coordinate systems

我们习惯地认为时间是均匀流逝的，时间坐标轴的刻度是均匀的，然而，广义相对论告诉我们，在本地局域坐标系上时间轴可以均匀刻度，一旦离开本地局域坐标系，把我们的时间轴转换到其他坐标系上，或者从其他坐标系观测我们的时间坐标轴时，我们本地所谓均匀的时间就发生了弯曲（不均匀流逝），这种弯曲程度与我们所处的引力势和相对于另一个坐标系原点的相对速度有关，简单关系如式（1）。

从上述例子可见，选择一个与脉冲星相对静止的坐标系是脉冲星导航的前提。对于遥远的脉冲星，把整个太阳系作为质点，脉冲星相对于该质点的径向匀速运动可理解为脉冲频率固有偏移，横向运动可理解为方位变化而脉冲频率不变，其他周期运动的影响通过长期观测可以修正，因而太阳系质心坐标系最接近这个条件。任何航天器上都必须把原子钟时间转换到太阳系质心系坐标时上，才能正确地测量脉冲星的脉冲周期和轮廓。

3 时间统一还是时间单位统一问题

脉冲星导航需要建立时空基准体系。选定空间坐标系，规定守时基准和传递方式是空间计量主要任务。在大尺度的广域时空中，不同坐标系之间相互传输的频率信息受到引力红移和多普勒效应的影响，导致频率不能成为最稳定的传递标准。时间具有客观唯一性，又能被原子钟准确测量，当约定光速为常数后，时间成为时空基准体系的重要参数。文献［6］的空间计量理论提出了两种时间统一的方法。

第一种是地球卫星导航系统GNSS 的时间统一，星载原子钟经过相对论公式修正，不再以SI 秒为单位测量原时（proper time），而是直接用修正后的计时单位（time unit 或称时间尺度）测量坐标时（coordinate time），不同轨道上使用不同的计时单位，由地面主控站守时并发布统一时间，在轨卫星定期与地面站比对时间，同时修正原子钟的时间或走速，保持与地面时间一致；

第二种是正确选择时空坐标系，以国际单位制SI 秒为计时单位测量原时，利用广义相对论的线元和时空度规表达式，计算“坐标时”，由此获得不同“原时”之间的比对关系，利用同一个坐标系中共同的“坐标时”来实现时间测量的统一。第一种时间统一的方法只能适用于地面和地球附近区域，而第二种方法适用于更广阔的太阳系。

GNSS 导航的时空基准体系是以地球质心为坐标原点O，每颗卫星不断地向四周发送自己的实时坐标和时间戳（对应坐标位置的时刻），如图3所示。时间统一的条件是：所有卫星发出的时间戳到达原点O 时都应相等，满足式（2）。因相对论效应影响和星载原子钟的不稳定性，每颗卫星的原子钟走速都不一致，它们不必以SI 秒为单位走时，但必须不断与地面站进行时间比对，确保与地心坐标时同步。因而GNSS 的星载原子钟并不用SI 秒测量原时，而是被驯服后直接测量坐标时，GNSS 导航卫星一般是圆轨道，其相对论效应影响近似为常量。

式中：to——坐标原点收到的时间戳；ti——第i 个卫星发出的时间戳，i 是卫星序号；Ri——第i 个卫星在坐标系中的位置矢量。

图3 GNSS 导航的时空基准模型示意图Fig.3 The principle of time-space standard mode of GNSS

第二种时间统一的方法更适合于广域空间的脉冲星导航。国际单位制SI 秒的绝对定义是航天器自主导航，不依赖于地面守时系统的前提。爱因斯坦的广义相对性原理：“一切参考系都是平权的，物理定律在任何坐标系下形式都不变，即具有广义协变性”。推广到空间计量领域“计量单位在任何参考系和任何局域空间中都应不改变其定义形式”。 1967年国际计量大会定义SI 秒：“铯原子C133 基态的两个超精细能级跃迁辐射振荡为9 192 631 770周期所持续的时间”［8］。此定义没有限制SI 秒的适用范围，因此无论是局域还是广域时空，无论是“原时”还是“坐标时”都必须使用上述定义的SI 秒作为时间尺度，来测量时间。广义相对论中有两种时间：“原时”是局域空间中使用SI 秒测量的时间；“坐标时”是以SI 秒为单位的时钟在引力场为零且相对坐标原点速度为零的那一点上测量的时间，惯性坐标框架中的质心点和无穷远点满足坐标时定义的条件。脉冲星相对于太阳系质心来说近似无穷远且静止，因此脉冲星和太阳系质心上有统一的坐标时。原时是可观测量，而坐标时只能利用原时积分获得。在同一个坐标系中不同局域的原时不能直接比较，只有换算到坐标时，才能相互比较。在广域大尺度时空中只能利用坐标时和SI 秒的绝对定义来统一时间。远离地球的航天器原子钟应以SI 秒为单位，测量脉冲星的到达光子数，先获得原时坐标轴上的测量值，再依据式（1）代入相对于OSSB的线对速度和局域引力势，积分获得OSSB坐标时，将原时坐标轴刻度换算为坐标时刻度。但速度和引力势（对应到位置上）都是导航的未知参数，又如何进行时间尺度换算呢？单独依靠脉冲光子的原时测量数据是不能进行脉冲星导航的，还必须借助一些已知的条件。

1）脉冲星的脉冲周期和轮廓的稳定性是已知的。地球观测站长期观测脉冲，利用已知的太阳系各天体轨道和引力势参数，将观测数据换算成以坐标时为刻度的脉冲周期，和每个脉冲到达坐标原点OBBS的时间，以及标准脉冲轮廓，这些已知量是脉冲星导航的基础，尤其是每个脉冲达到坐标原点的时间能外推到未来某一时刻，这就是脉冲星的星历表。在不断积累的大量数据支持下星历表预测更佳准确；

2）脉冲星方位是已知的。遥远的银河系外恒星是太阳质心坐标系的参照物，经长期观测被选为导航参照的脉冲星具有长期的方位稳定性；

3）多普勒效应是可修正的。航天器借助星敏感器和太阳敏感器，利用现有天文导航技术初步确定航天器在太阳质心坐标系内的位置、速度和方向，虽然太阳质心不同于太阳系质心，但距离较远时，速度测量偏差是小量。已知航天器在太阳质心坐标系内的速度矢量和脉冲星方位矢量，点积成为标量速度是航天器在太阳质心坐标系中在脉冲星视向方向的运动速度，可将V 代入在航天器自身坐标系内修正多普勒效应［9］

式中：Δτ’——修正后的原时坐标刻度间隔；Δτ——修正前的原时坐标刻度间隔；V——航天器在脉冲星视向方向相对于脉冲星的速度，接近脉冲星为正，远离脉冲星为负。

这一时刻，所测量的原时坐标轴乘以多普勒效应系数（式2 中的系数），拉伸或压缩时间坐标轴，这样处理后的原时数据才可在式（1）中进行时间尺度转换。精确导航计算中这一步所述的速度需要多次迭代。

4）时间单位SI 秒是绝对定义的。航天器上的原子钟必须使用SI 秒测量原时，否则时间尺度转换后的坐标时与星历表时间不能统一。时间单位统一是空间计量的第二种时间统一方式的前提条件。把式（1）左边时间间隔Δt 为作为星历表给出的脉冲周期，右边原时τ 是可测量，用两个及以上脉冲星的星历就可迭代计算相对原点速度和引力势。但这种方法中速度和引力势都是与c－2相关小量，计算程序的截断误差影响很大；

5）星历表初始历元是已知的。当某一颗脉冲星的星历表初始历元确定后，后续脉冲都能获得顺序的编号，且对应其到达OSSB的坐标时历元，即序号乘以脉冲周期。一旦航天器对新探测到的每个脉冲，查找到它在星历表中的编号，那么后续测量的脉冲相位就可知道航天器在脉冲星视向方向的位移，观测多个不同方向的脉冲星可知航天器在太阳系质心坐标系的具体位置。把毫秒脉冲星的脉冲间隔换算到空间，在视向方向达几千千米的尺度，利用传统天文导航技术可初步获得航天器的位置和速度，以此估算新到达的脉冲编号。

4 大尺度广域时空的守时系统

守时是维持时间系统的稳定并且统一时间基准的技术。如果一个孤立的系统不需要与外界比较时间的话，就没有统一时间的需要，也就没必要研究空间计量了。然而，人类活动的所有空间范围和所有时间跨度都被时间联系在一起，尤其是长度单位被光速和时间定义后，空间也成为时间的相关量，导航的基本观测量就是时间。时间基准稳不稳，时间测量准不准以及时间如何传递和比较的问题成为空间计量的基本问题。自从原子钟技术实用以来，历经50 多年，在地球上建成了基于大地水准面和500 多台高精度原子钟的守时系统，提供国际原子时TAI 基准，发布国际协调时UTC 时间。当人类远离地球，开展深空探索或建立地球以外的基地时，就不方便使用地面的守时技术，在大尺度广域时空中，需要构建新的守时系统—太阳系质心守时系统。与现有守时系统不同之处如下。

1）新的守时系统是以太阳系质心为坐标原点，在广义相对论基础上把坐标时作为时间传递、比对和守时的通用语言，不限定守时基准所处的空间位置，既可以在地球表面，也可以在地球同步轨道以及拉格朗日L2 点，未来还可以在月球、火星基地建立守时基准，只要守时基准位置的引力势和相对速度可以精确计算就可行；现有守时系统是以地球质心为坐标原点，为便于地面原子钟的测量，把地球质心坐标时外推到大地水准面上，称大地水准面上的时间TT，也被看作是一种“坐标时”，它与地心坐标时TCG 有固定的走速偏差；

2）新的守时系统利用原子钟和脉冲星的稳定性，有微观量子稳定和宏观宇宙稳定的双重互比参考，现有守时系统仅依赖于多台原子钟的加权平均，来维持时间系统的稳定；

3）新的守时系统是开放系统，它把地面守时系统作为权值最大的子系统，随着人类向外空间的发展，它还可以加入更多行星守时子系统，甚至引力势和相对速度确定的任何航天器，如拉格朗日L2点，也能成为守时系统的一部分。

新的守时系统框图如图4所示。具有守时功能的航天器应具有测量多颗X 射线脉冲的能力，并携带铯原子钟，航天器的轨道力学参数作为已知参数，用铯原子钟复现SI 秒单位，测量脉冲星到达时间，将某一编号的脉冲贴上转换为太阳系质心坐标时的脉冲到达时间TOA，发送到地面，在地面计算来自不同航天器的TOA 与星历表之差。若偏差整体偏移，则修正星历表，若某一个航天器的偏差较大，则通知该航天器修正铯原子频标或轨道参数。守时系统的计算与脉冲星导航的计算是互逆过程。脉冲星导航是已知星历表和原子时钟，计算轨道参数。而守时则相反。

图4 太阳系质心坐标系守时系统框图Fig.4 Time keeping system of BCRS

5 结束语