频域滤波产生的时域端点效应及避免方法

王 颜

1 频域滤波产生的时域端点效应

滤波是数字信号处理中的常见过程。通过选频滤波可以提取时域信号有用的频率分量，压制干扰信号。选频滤波通常在频域进行，其具体步骤是：

（1）对长度为N 的时域信号x（n）作离散傅里叶变换（DFT），得到对应的频域信号X（k）。通常使用快速傅里叶变换算法（FFT）进行。

（2）将频域信号X（k）各点处的值与频域滤波器F（k）相同频率处的值相乘，得到滤波后的频域信号Y（k）：

（3）对 Y（k）做离散傅里叶反变换（IDFT），即得到频域滤波后的时域信号 y（n）。通常使用快速傅里叶反变换算法（IFFT）进行。

对时域信号进行频域滤波后所得到的信号可能在时域的一端被截断，被截去的部分在另一端出现，造成时域信号失真。本文称这种时域信号截断和移位造成的信号失真为频域滤波的时域端点效应。下文通过编写MATLAB 程序，应用式（2）所表示的带余弦镶边的带通滤波器对地震勘探数据处理中广泛应用的雷克子波[1]进行频域滤波，说明频域滤波的流程，并指出这一过程产生的时域截断和移位现象，即频域滤波的时域端点效应。

式（2）中，l1和h1分别是低频端和高频端的截止频率，l1-l2和h1-h2分别是低频端和高频端的过渡带，在过渡带内滤波器的幅值以余弦函数的形式从1 衰减到0. 显然，对于连续的频率，该滤波器的频谱是光滑的。

现将滤波器低频端和高频端的截止频率分别设为20Hz，60Hz，过渡带宽度设为 3Hz，即 l2=16，l1=20，h1=60，h2=64，则滤波器的频谱如图1 所示。

图2 和图 3 分别是主频 40Hz 的雷克子波信号及其频谱。

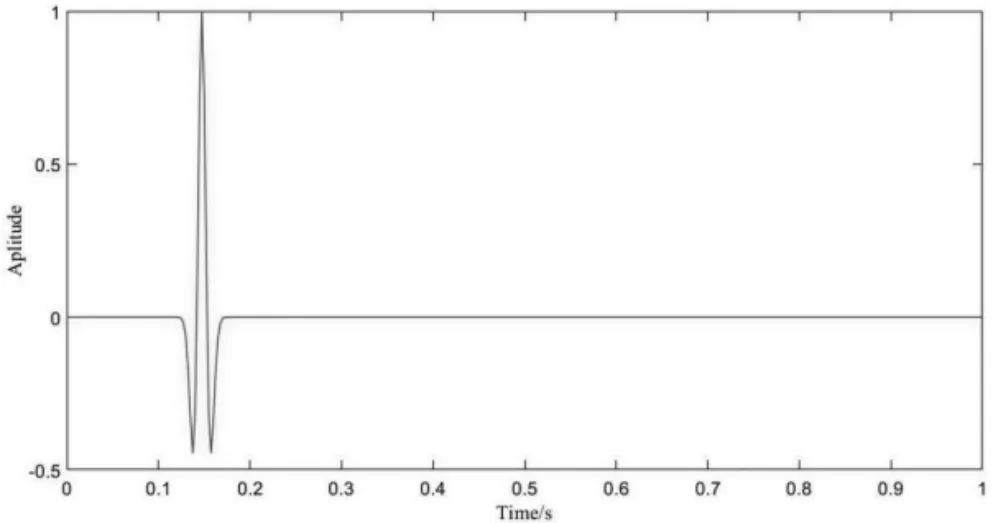
图2 40Hz 的雷克子波信号

图4 和图5 分别是应用图1 所示滤波器进行步骤（2）所述滤波后的信号的频谱和经过离散傅里叶反变换后所得的时域信号。

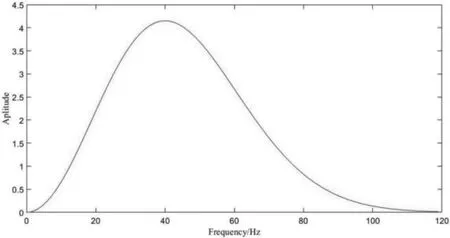
图3 40Hz 对应的频谱

图4 滤波后的信号的频谱

图5 经过离散傅里叶反变换后所得的时域信号

从图5 可以看出，滤波后的信号在t=0 处被截断，被截去的部分出现在了时间轴的末端，即出现了前文所述的端点效应。

2 端点效应产生的原因分析

根据离散傅里叶变换和反变换的性质[2]，对频域信号进行点数为N 的等间隔采样，其离散傅里叶反变换对应的时域信号为

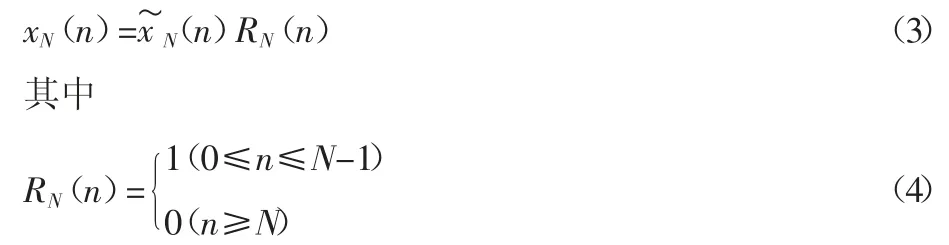
由（3）式可知，如果原来的时域信号x（n）经过频域滤波后对应的延伸至a ≤n ＜0 范围内，则这段信号会被截除，同时因为被截除的信号会出现在时间轴末端的a+N ≤n ≤N-1 位置。类似的，如果延伸至N ≤n ≤b 范围内，这段信号同样会被截除，并出现在0≤n ≤b-N 位置。

3 频域滤波中避免时域端点效应的原理

本文现从时域和频域运算间的关系角度分析为避免时域端点效应，频域滤波过程应满足的条件。

由傅里叶变换的性质可知，频域的乘积运算等价于时域的卷积运算，所以。

由上式可知经过频域滤波后的信号相当于原信号在时域与滤波器的时域响应做卷积运算的结果。假设x（n）和 f（n）在时间轴上的第一个和最后一个非零值出现的位置分别为 N1、N2和 N3、N4，滤波后的信号为 xf（n），则：

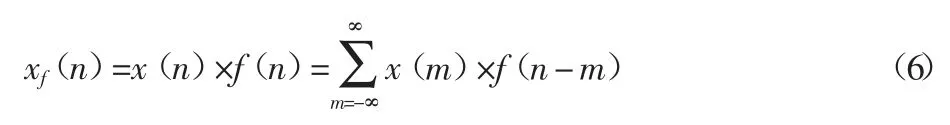
若xf（x）≠0，则x（m）≠0 且f（n-m）≠0，所以m ≤N2，nm ≤ N4，两式相加得。

由（7）式可知，原信号的采样总时长N 满足（8）式时，可以确保滤波后的信号在时间轴末端不被截断。

（8）式可以变形为

因为对于傅里叶反变换，时间轴的两个方向是等价的，所以由（9）可以得到确保滤波后的信号在时间轴起始端不被截断的条件。

（9）式和（11）式指出了原信号和滤波器的参数满足什么条件时，可以保证经过频域滤波的信号在时域不出现端点效应。从推导过程可以看出，这两个不等式表达的是避免时域端点效应的充分条件，而非必要条件。所以若频域滤波过程中出现了时域端点效应，可以按满足（8）（11）两式的方向调整相关参数，但相关参数并非必须满足两式才能避免端点效应。

4 避免时域端点效应的方法及实验验证

本节介绍了避免频域滤波的时域端点效应的两种具体的方法，并以滤波后的信号在时间轴起始端被截断造成的端点效应为例，通过MATLAB 程序进行了实验验证。

4.1 时域补零

通过在原信号的末端增加M 个零值点，可使式（8）中的N增大M 而N2、N4不变，各参数整体向满足该不等式变化，因此当M 大于某个值时，信号在时间轴末端被截断造成的端点效应会得到避免。

类似的，通过在原信号的起始端增加M 个零值点，可使式（11）中的N、N1各增大M。因为频域采样点数增加了M，所以滤波器的离散傅里叶反变换时长增加了M，由离散傅里叶反变换结果的对称性可知，N3增大了M/2。因此（11）式左端增大了M，右端增大了3M/2，各参数整体向满足该不等式变化，因此当M大于某个值时，信号在时间轴起始端被截断造成的端点效应会得到避免。

在图2 所示信号起始端增加100 个零值点，得到图6 所示延时0.25s 后的信号。

图6 延时0.25s 后的信号

根据离散傅里叶变换的性质，信号的频谱（振幅谱）不发生变化，且仍为均匀采样，但采样数比原来增加100，采样间隔变小。因此要通过频域滤波获取与第一节中相同的频率成分，所使用的滤波器应满足连续频谱与第一节实验中的滤波器相同，但采样位置与图6 信号频谱的采样位置相同。该滤波器的频谱如图 7 所示。

图7 与图6 信号频谱的采样位置相同下的滤波器频谱

图8 红线和蓝线分别是第一节的实验和本实验所用滤波器的时域响应，可以看出蓝线第一个非零值的位置比红线增大了50，与理论分析相符。

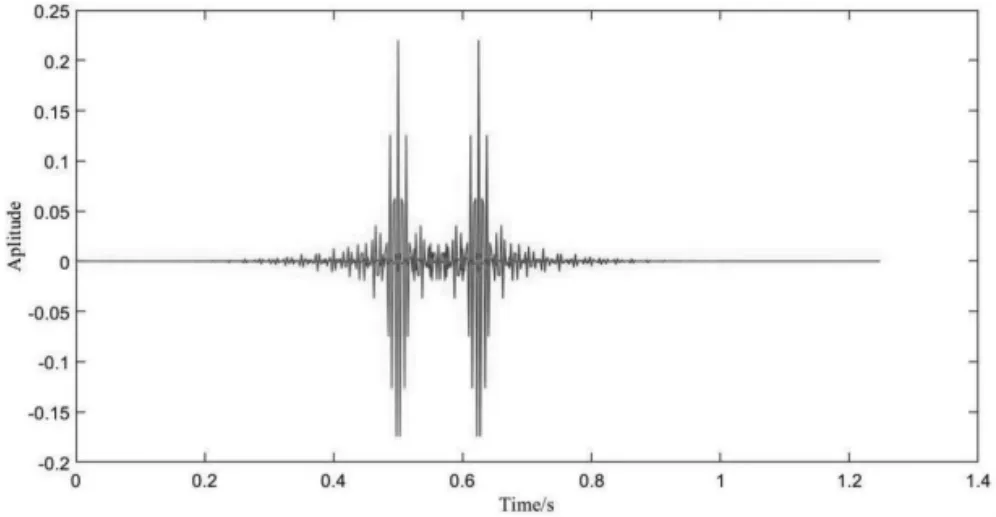
图8 不同实验所用滤波器的时域响应

图9 是经过频域滤波得到的时域信号，可见图5 中的端点效应消失，证明了时域补零方法的有效性。

图9 经过频域滤波得到的时域信号

4.2 拓宽滤波器频谱

通过拓宽滤波器频谱，使其时域响应变窄，（8）式中的N4变小，（11）式中的N3 变大，两式中的参数都向使不等式成立的方向变化。因此信号在时间轴起始端和末端被截断造成的端点效应都可以通过拓宽滤波器频谱来解决。

将第一节实验所用滤波器的过渡带宽度增加到9Hz，其频谱如图10 所示。

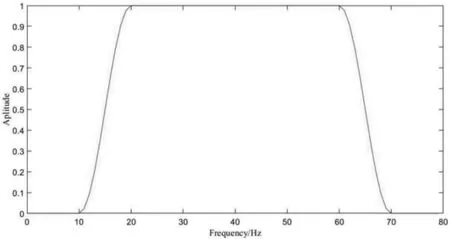
图1 0 滤波器过渡带宽度增加到9Hz 时的频谱

图11 红线和蓝线分别是第一节的实验和本实验所用滤波器的时域响应，可以看出本实验滤波器的时域响应变窄，第一个零值点位置后移，最后一个零值点位置前移。

图12 是用过渡带宽度增加的滤波器对图2 所示信号进行频域滤波的结果，可见图5 中的端点效应消失，证明了拓宽滤波器频谱方法的有效性。同时因为滤波器的过渡带变得更加平缓，吉布斯效应也得以减弱。

图11 不同实验所用滤波器的时域响应

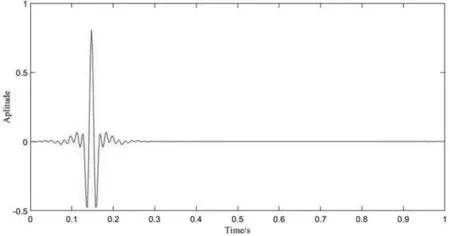
图12 经过频域滤波得到的时域信号

5 结论

对数字信号进行频域滤波所得到的时域信号可能在一端被截断，被截去的部分出现在另一端，造成时域信号失真。本文称这一现象为频域滤波的时域端点效应。通过理论分析和数值实验，得出以下结论：

（1）频域滤波的时域端点效应产生的原因是原信号经过频域滤波后时宽变长，因采样总时长有限而在一端或两端被截断。同时因为频域信号对应的时域信号的周期性，在一端被截除的信号在另一端重现。

（2）假设原信号采样总时长为N，原信号和滤波器的时域响应在时间轴上的第一个和最后一个非零值出现的位置分别为 N1、N2和 N3、N4，则上述参数满足 N-1≤N1+N3可以确保不出现信号在起始端被截断造成的端点效应；满足N-1≥N2+N4可以确保不出现信号在末端被截断造成的端点效应。

（3）若频域滤波过程中出现了时域端点效应，可以按满足结论（2）中的两个不等式的方向调整相关参数。但因为这两个不等式表达的是避免时域端点效应的充分条件而非必要条件，所以调整后参数并非必须满足两式。

（4）通过在原信号的起始端补零，可以避免滤波后的信号在起始端被截断造成的端点效应；在原信号的末端补零，可以避免滤波后的信号在末端被截断造成的端点效应。

（5）通过拓宽滤波器频谱，信号在时间轴起始端和末端被截断造成的端点效应都可以得到解决。