OFDM 系统中的符号时域偏差估计

崔国丽

（93995 部队，陕西 西安 710000）

0 引言

正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）技术以其自身的高传输速率、抗选择性衰落能力强以及硬件结构相对简单等优势，得到了长足的发展［1］。由于自身的优越性，其不仅在民用领域得到大量应用，在军事通信领域也得到大量的应用［2］。

要保证OFDM 系统能发挥其自身优势，需要保证各个子载波之间的正交性，只有这样才能保证OFDM 系统可以正确地传输数据消息。要解决各个子载波之间的正交性，需要解决频率选择性信道所引起的失真［3］。由发送端至接收端，时域和频域的偏差都会影响子载波之间的正交性［4］。本文主要研究时域偏差所引起的数据变化，并根据数据变化来估算时域的偏差值。

1 符号时域偏差估计技术

在OFDM 系统中，如果符号时域偏差较小，会引起相位失真。如果只发生相位失真，可以通过均衡器进行调整，以此消除符号时域偏差所引起的相位失真。当符号时域偏差较大，会引起码间干扰（Inter Symbol Interference，ISI），此时通过均衡器就难以实现系统的修正。在实际的OFDM 系统中，接收端必须使用同步技术来评估时域的偏差值，以便在接收端获得OFDM 信号的起始点，以此保证接收端接收符号的准确性。符号时域偏差的估计方法有很多种，本文主要讨论基于循环前缀的估计方法［5］。

在OFDM 系统中，由于多径信道的影响，若OFDM 符号之间没有保护间隔，必然会引起相邻符号间的码间干扰。为了克服多径信道的影响，系统会在OFDM 符号之间插入保护间隔。对于保护间隔之间的填充数据，有三种常用的填充方法，分别为补零填充、循环前缀填充以及循环后缀填充。本文重点研究基于循环前缀填充进行的符号时域偏差估计。设保护间隔的长度为TG，一个OFDM 符号的有效长度为Tsub，循环前缀填充就是将Tsub的后TG长度复制到保护间隔。这样一个完整的OFDM符号长度为Tsym=TG+Tsub。TG为保护间隔的长度，Tsub为OFDM 符号的有效长度。保护间隔中的TG数据是Tsub后TG长度的数据副本［6］。

如图1 所示，保护间隔为对应OFDM 符号最后一部分的副本。在发送端，保护间隔的数据与OFDM 符号最后一部分的数据相同，通过这种相同关系来进行符号时域偏差的估计。设保护间隔的数据有NG个采样值，OFDM符号的数据有Nsub个采样值。设定两个滑动窗口中每个窗口的长度为NG，两个滑动窗口的间隔为Nsub，两个滑动窗口同时滑动，当两个滑动窗口中的数据相似度最高，此时的采样点位置就是所要估计的符号时域偏差值［7］。

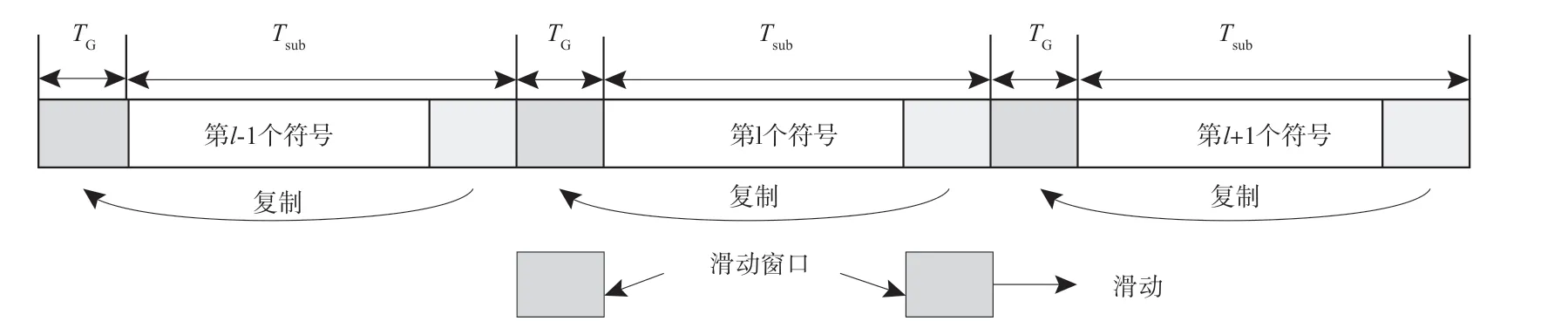
图1 基于循环前缀的符号时域偏差估计方法

两个滑动窗口相似度最高的判定方法有很多种，最简单的方法是对两个滑动窗口之间的数据求差值。当差值最小，就是两个滑动窗口相似度最高的时候，如式（1）所示。式（1）达到最小时的δ就是所要估计的符号时域偏差值。

式中：yl为第l个符号，N是符号的总长度，n为符号的起始位置。

式（1）中的方法最为简单，但是难以适应信道的复杂性。当信道或接收系统中存在一定的频域偏差，再使用式（1）时，就会出现性能下降的问题。为了应对信道或接收系统中的频域偏差问题，可通过两个滑动窗口采样数据差值的平方结果来估计符号时域偏差值，计算方法如式2 所示。

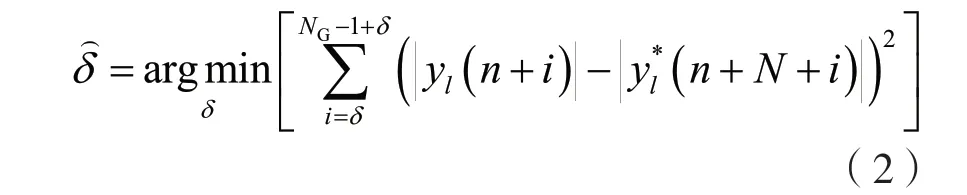
式（1）和式（2）的原理都是通过两个滑动窗口的采样数据差值来估计符号时域偏差。通过两个滑动窗口的相关性也可以估计符号时域偏差值，计算方法如式3 所示。

2 仿真结果

本文对基于循环前缀的估计方法进行了仿真，仿真计算过程使用式（2）和式（3）的计算方法。图2 和图3 分别为在不同频率偏差的情况下相关法和差值最小法计算结果的对比。可以看出，相关法最大值对应的采样位置和差值最小值对应的采样位置是一致的。

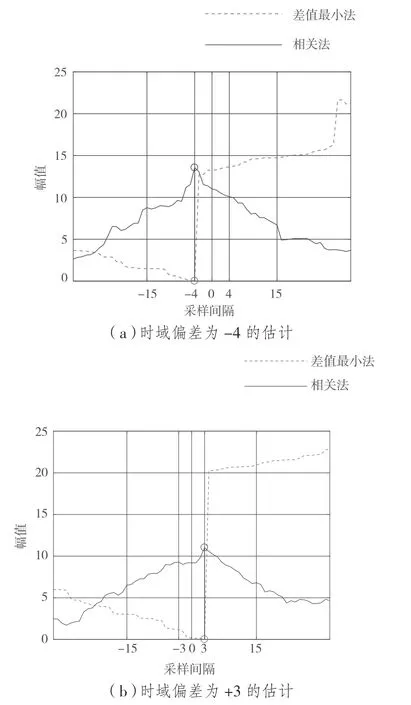
图3 存在一定频域偏差时对时域正负向偏差的估计

图2 为没有频域偏差时，符号时域偏差为-3和+4 两种情况的偏差估计。图2（a）为符号时域偏差为-3 时的相关法（蓝线）和差值最小法（红线）的计算过程。相关法的最大值和差值最小法的最小值就是估计的符号时域偏差值。图2（b）为符号时域偏差+4 时的计算过程。由图2 可以看出两种方法估计出的符号时域偏差值一致，也和预设的符号时域偏差值一致。

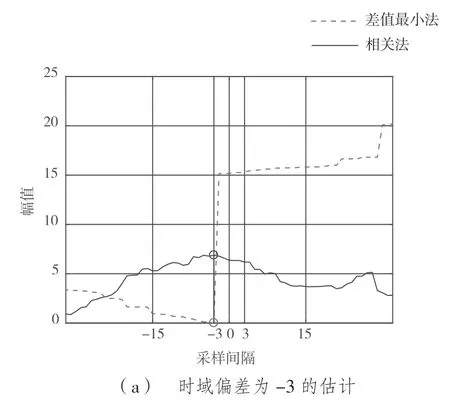
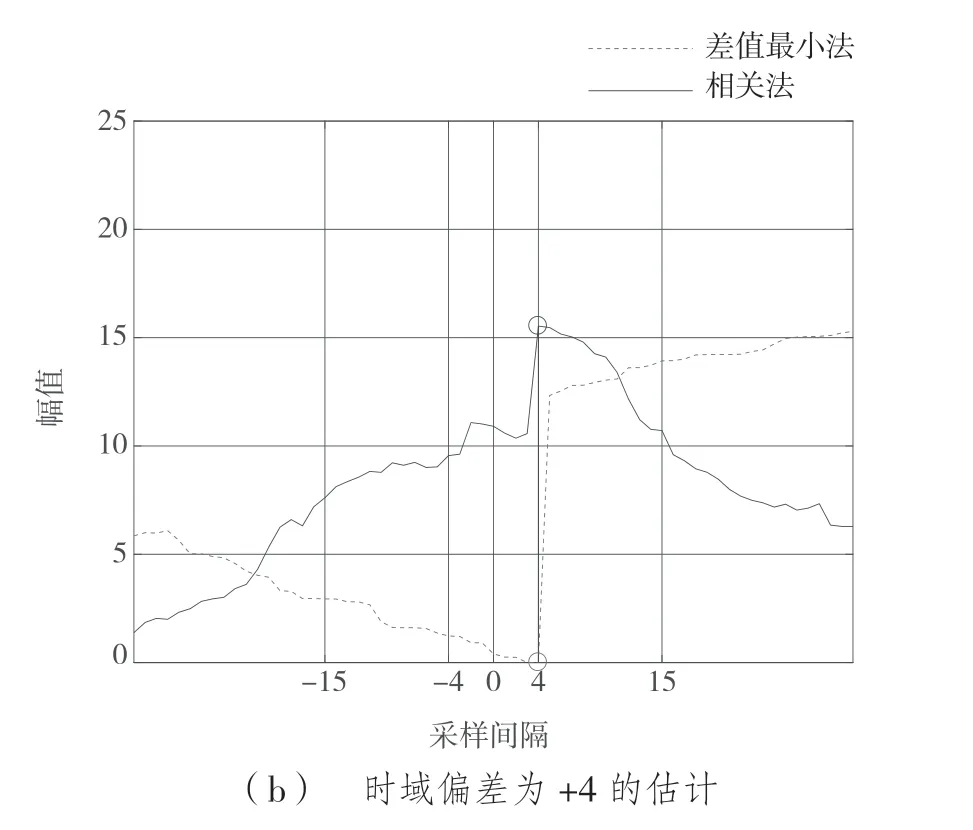
图2 没有频域偏差时对时域正负向偏差的估计

图3 为归一化频域偏差值为0.5 时，符号时域偏差为-4 和+3 两种情况的偏差估计。图3 中的曲线情况和图2 一致。由图3 可以看出，在频域偏差不太大的情况下，两种方法估计出的符号时域偏差值一致，并且和预设的符号时域偏差值一致。

3 结语

本文主要研究了OFDM 系统同步技术中的符号时域偏差的估计技术。符号时域偏差的估计技术有很多种，常用的是基于循环前缀的符号时域偏差估计方法和基于训练符号的符号时域偏差估计方法。本文重点分析了在没有频域偏差和频域偏差较小的情况下，循环前缀的符号时域偏差估计方法的正确性。通过仿真结果可以看出，相关性和最小差值法都可以正确地估计出符号时域偏差值。本文研究的情况比较理想化，并没有考虑频域偏差较大以及多径效应比较明显的情况。后续会进一步研究上述情况下的符号时域偏差的估计方法。