解三角形中的角平分线、中线、高线问题

严国华

(湖南省长沙县实验中学)

近年来,解三角形问题在高考题和模拟题中难度有所提升,对学生数学运算能力和平面几何知识的掌握程度要求更高了.其中有一类涉及中线、高线和角平分线的解三角形问题经常出现,这类问题是解三角形内容的延伸,是高考考查的热点.它既可以有效地考查解三角形的相关知识,又能考查三角形中这些特殊线段的性质,对学生的数学运算、逻辑推理、综合解题能力都有较高的要求.下面举例说明这类问题常见题型及解题思路,以供读者参考.

1 与中线有关的问题

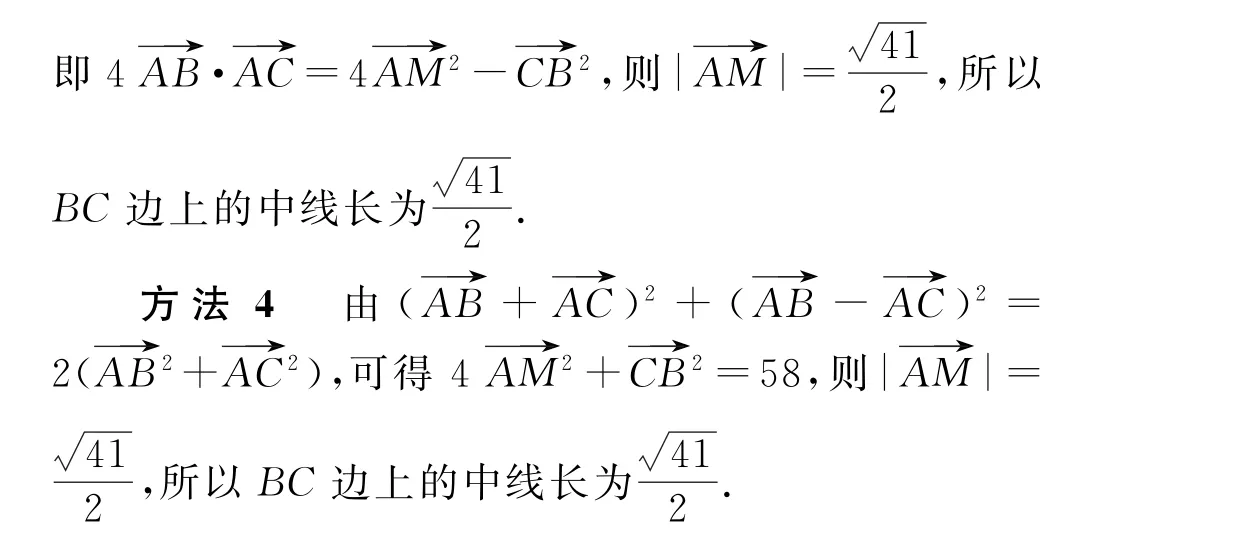
图1

2 与内角平分线有关的问题

例2 在△ABC中,已知AB＝2,AC＝1,D为BC边上的点.若AD平分∠BAC,求线段AD长的取值范围.

与角平分线有关的问题可以从以下两个方面进行思考.1)方程思想的应用:利用等面积法构造出关于内角平分线长的方程进行求解;2)转化思想的应用:利用内角平分线定理把解三角形问题转化为三角函数和向量问题进行求解.

3 与高线有关的问题

A.当h＞3时,n＝0

B.当h＝3时,n＝1

C.当0＜h≤1时,n＝0

D.当1＜h＜3时,n＝2

图2

与高线有关的问题可以从以下几个方面进行思考.1)根据等面积法把高的比例转化成对应边的比例,再利用余弦定理进行求解;2)利用平面几何知识,通过解直角三角形求解;3)从三角形的高线很容易联想到任意三角形射影定理:在△ABC中,a＝bcosC＋ccosB,b＝ccosA＋acosC,c＝bcosA＋acosB.

4 与中线、角平分线和高线有关的面积问题

例6 如图3 所示,在△ABC中,内角A,B,C的对边分别为a,b,c,已知b＝3,c＝6,sin2C＝sinB,且AD为BC边上的中线,AE为∠BAC的角平分线.

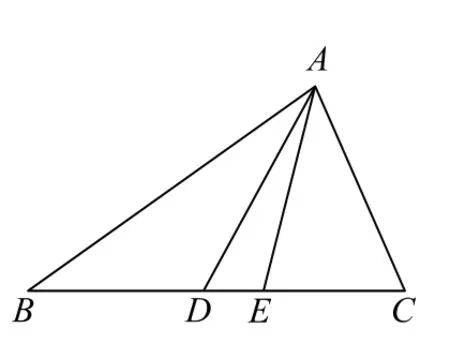
图3

(1)求cosC及线段BC的长;

(2)求△ADE的面积.

求三角形面积的最值是一种常见的题型,主要方法有两类,一是找到边之间的关系,利用基本不等式求最值.二是转化为关于某个角的函数,判断角度的取值范围,利用函数思想求最值.

与三角形中线、高线和角平分线有关的解三角形问题,其本质上是求解组合三角形的问题,解决这类问题,除了需要掌握与中线、高线和角平分线相关的知识外,还需要考虑怎样将题目中的元素集中起来,充分利用三角变换公式、平面几何、平面向量、函数和不等式等知识,有效进行转化和化归.