2021年强基计划校考试题分析

赵芳玲

(甘肃省定西市安定区交通路中学)

2020年起,教育部在部分“双一流高校”开展基础学科招生改革试点工作,也称为强基计划,不再组织高校开展自主招生工作.强基计划的功能在于选拔人才,因此对思维能力有一定的要求,从试题中也不难发现这一特点.本文以2021年武汉大学强基计划试题为例,对强基计划试题考向进行分析,希望能给读者带来备考启示.

1 落实核心素养,强化数学思维

图1

通过所绘制的函数图像能够较好地落实学生的数学抽象素养,本题看似一个问题,其实质上从4个角度对函数的极值进行了考查.

2 灵活与发散性思维并存,兼顾知识的广阔性

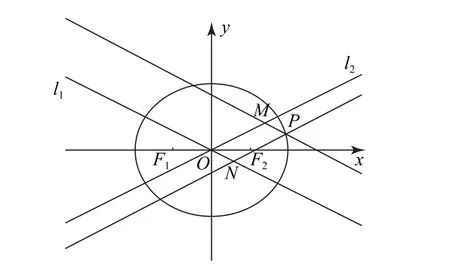
图2

直线与椭圆的位置关系一直是高考试题中的常考内容,但本题改变了以往的考查形式,考查了两条直线与椭圆的相交问题,对学生的思维能力进行了充分检测.

3 以高等数学为背景,覆盖全面

例3 (第13题)设复数z的实部和虚部都是整数,则( ).

A.z2-z的实部能被2整除

B.z3-z的实部能被3整除

C.z4-z的实部能被4整除

D.z5-z的实部能被5整除

因为z2-z＝a2-a-b2＋(2ab-b)i＝a(a-1)-b2＋(2ab-b)i,a(a-1)可以被2整除,当b为奇数时,a(a-1)-b2不能被2整除,故A 错误.

因为z3-z＝a3-a-3ab2＋(3a2b-b3-b)i,由费马小定理得a3-a能被3整除,故B正确.

z4-z的实部为a4-6a2b2＋b4-a,当a,b为奇数时a4-6a2b2＋b4-a也为奇数,故不能被4整除,故C错误.

z5-z的实部为a5-a-10a3b2＋5ab4,由费马小定理得a5-a能被5 整除,故a5-a-10a3b2＋5ab4能被5整除,故D 正确.

综上,选BD.

强基计划试题的命题人大多是高校教师,因此部分试题会结合大学知识进行考查,本题中的整除概念就来自于高等代数的内容,费马小定理也是大学所学习的数学知识.

4 源于高考真题,变式深化题源

对于B,因为f(x＋2π)＝sin(x＋2π)sin2(x＋2π)＝sinxsin2x＝f(x),所以f(x)＝sinxsin2x是以2π为周期的周期函数,函数图像如图3所示.

图3

方程f(x)＝a在[0,2π)内解的个数为偶数,故B正确.

对于C,因为f(x)＝sinxsin 2x,所以f(π＋x)＝sin(π＋x)sin2(π＋x)＝-sinxsin2x,f(π-x)＝sin(π-x)sin2(π-x)＝-sinxsin2x,

所以f(π-x)＝f(π＋x),则x＝π为f(x)的一条对称轴,故C正确.

对于D,因为f(x)＝sinxsin2x,所以

综上,选A.

本题主要考查了三元均值不等式、函数的周期性与对称性,该题所给出的函数f(x)与2018年新课标全国Ⅰ卷理科第16 题中所给的函数f(x)＝2sinx＋sin2x相似,仅把式子中的加号变为了乘号,去掉了常数2.