关注三角函数中的常见解题误区
2022-10-23 07:19:02毛世勤
高中数理化 2022年17期
毛世勤
(青岛市城阳第一高级中学)
求解三角函数题时,往往会因为没有挖掘隐含条件而出现各种各样的错误,因此归类整理三角函数中的常见解题误区就显得非常重要.本文结合例题进行剖析,旨在帮助学生明确“误”之因,认识“误”之道.
1 没有充分考虑角的取值范围


本题如果利用正弦值分析(解法1),则极易出错;如果利用余弦值分析(解法2)或者利用正切值分析(解法3),则不易出错.请想一想,为什么?

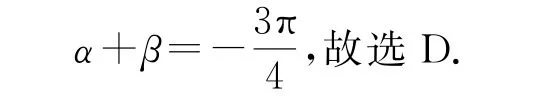
求解本题的关键在于充分利用根与系数的关系,将角α,β的取值范围缩小.
2 没有充分考虑正弦、余弦函数的有界性

在挖掘本题的隐含条件时,不但要考虑sinx的有界性,而且要考虑siny的有界性,否则极易出错.
3 没有充分利用锐角三角形


综上,关注三角函数试题常见解题误区,不仅有利于加深对相关数学知识的准确理解,还有利于不断积累解题经验,提高解题思维能力,有效避免一些常见错误,进而提升解题的速度和准确性.
猜你喜欢
语数外学习·初中版(2023年6期)2023-08-03 07:18:47
中等数学(2021年9期)2021-11-22 08:06:58
中等数学(2021年8期)2021-11-22 07:53:36
女子世界(2017年12期)2017-05-22 02:53:43
小学生学习指导(中年级)(2017年4期)2017-03-20 15:47:04
中国卫生(2016年9期)2016-11-12 13:27:58
学周刊(2016年26期)2016-09-08 09:02:56
中学生数理化·七年级数学人教版(2015年5期)2015-05-30 10:48:04
汽车之友(2015年6期)2015-03-18 05:15:08
中国信息化周报(2014年41期)2014-11-07 03:13:40

