向量“圆”析构建新课堂 核心素养探究新教材——基于数学核心素养的平面向量微专题课例

徐成周

(济南大学城实验高级中学)

基于培养学生解决平面向量问题能力的主要目标,根据我校高一学生的实际学情,以微专题的教学模式设计教学方案,充分发挥教师的引导作用和调动学生的主观能动性,提高学生的数学思维参与度,深化学生求解平面向量问题的能力,助力提高学生的数学核心素养.

1 问题提出的背景

高中数学教学侧重于按照教材中的章节内容开展数学知识的讲解,或者以“对点训练”的方式,进行解题思维的培养.这些方式虽然可以较为全面地使学生掌握数学知识,但是从宏观的角度看,不利于学生脉络清晰地构建完整的数学知识体系.如果可以在高中数学教学中,融入微专题的教学模式,那么既有利于督促学生构建完整的数学知识体系,疏通知识脉络,又可以高效提高学生的解题能力.

1.1 微专题的含义

微专题课程,即将教学过程中的某一类问题,经过筛选、整理、提炼,凝练为一个教学课题,开展学科课程教研.微专题经常选用一些价值高、有意义、科学有效的小型专题作为教学的切入点,可以对学生进行专项训练,具有“切口小、周期短、时效高”的基本特征,从而达到“课程解决问题,专项研究对策,学习结果扎实”的成效.

1.2 微专题教学模式融入高中数学教学的重要性

在“双减”背景下,微专题教学可以简明扼要地在教师指导下开展教学活动,防止学生在数学学习中一味地采用“题海战术”,可极大地降低学生的学习负担,使数学学习变得高效.

例如,教师在开展“平面向量”这部分知识教学时,发现大多数学生不能做到“学以致用、举一反三、一题多解、灵活通融”,经常以一种思维模式思考题目,从而走入死胡同.此时设计以平面向量解题为主题的微专题,可以促使他们在解题中更加准确地进行判断与决策,及时采用最优的思维方式进行思考.与此同时,微专题教学模式下的数学课堂灵活性强,并将前、后知识模块进行多方面联系,极大地促进学生对数学知识内在本质的探索与理解,从而全方位提高学生的数学核心素养.

1.3 微专题教学模式的基本原则

1)精准打击,逐个击破

微专题可以分解为“微”和“专题”,是通过小课题、小专题的方式对教学知识进行深化处理.例如,对于“立体几何、统计与概率”这样的大专题知识进行更加细致地解剖和分析,做到精准打击、点点击破,帮助学生进行查缺补漏.

2)以生为本,深化思维

微专题教学模式的构建是建立在教师对高中学生认知结构的了解基础上,强化学生在教学活动中的主体地位.因此,教师要深入了解高中学生在数学上的认知结构,教学要遵循学生的学习规律.教师要采用有效的方式帮助学生调动自身的学习思维,从而从本质上切实提高他们学习的效率.

3)见微知著,融会贯通

教学是教师的“教”和学生的“学”的交互过程,只有教和学有机结合、相互促进,才能真正地达到教学目的.开展微专题教学,可以使学生注意到平时练习中忽视的问题,对潜藏的薄弱之处进行查缺补漏;可以使教师对教材和学生进行更加深入的了解.通过微专题学习,学生可以对知识点进行整理归纳以及重构,将知识点和题目进行连接,对题目进行对比,真正做到融会贯通.

2 微专题教学课程设计——以平面向量问题教学为例

2.1 教材内容分析

向量作为沟通“代数”“几何”“三角”的桥梁,对中学数学知识框架的构建起着更新和完善的作用,是从丰富的生活实际和物理素材中抽象出来的.向量具有丰富的代数运算法则,与之前所学的代数运算具有相似之处,也有不同之处;向量是一种工具,兼具“代数”和“几何”的属性.解决向量相关题目要让学生去体会在不同角度下的思维模式,进而提高提出问题、分析问题、解决问题的能力.

2.2 教学目标设置

提高学生充分挖掘题目几何特性的能力,从代数视角研究向量的同时,可以在几何的思维方式下,具体形象地思考问题,从而找到题目的最优解.

充分挖掘题目中条件和结论的关系,体会其中的形成过程,培养学生观察、联系、类比、抽象、概括、归纳、实践等方面的能力.

2.3 学生学情分析

在解决平面向量问题时,学生习惯性采用代数的方法,有时经过大量的计算而不得其解.若从图形视角来思考具有丰富几何内涵的向量问题,有时会迎刃而解.

2.4 教学策略分析

采用“问题串”的教学方法,通过“抛出问题,引导学生思路,教师点拨引导”三者结合,促进学生的理解和掌握.

在设置“问题串”时,注意题目侧重点类型的多样性,题目和题目之间具有难度梯度,层层深入,做到模块与模块之间的有机联系和整合.

2.5 教学方法与教学手段

1)问题引导教学法

2)“问题串”式启发教学

3)小组合作探究学习

2.6 教学过程

1)温故知新

教师:什么是向量?

学生:向量是既有大小又有方向的量.

教师:向量的大小是向量的代数特征,向量的方向是向量的几何特征,向量具有“代数”和“几何”的二重性,今天我们重点从“几何”的角度来研究向量问题.

设计意图 通过向量的定义引出向量的二重性,温故而知新,深入挖掘向量的特征.

2)因势利导——从几何的角度研究向量问题

教师:向量a,b如图1所示,利用向量加法的三角形法则作出a＋b;向量a,b如图2所示,利用向量加法的平行四边形法则作出a＋b.

学生:

图4

设计意图 从基本知识点切入,引导学生从几何的角度来思考向量的运算问题.

3)牛刀小试

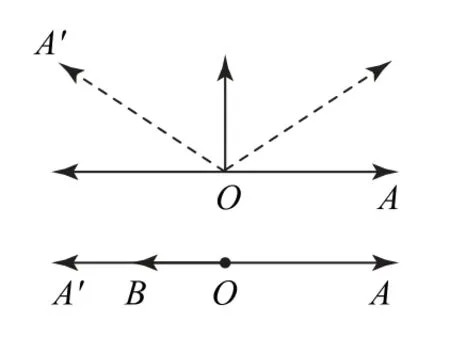
图5

设计意图 从基础题入手,引导学生从几何的角度剖析题目条件,作出相应图形,从而分析出答案.

问题2 设向量a,b,c满足a＋b＋c＝0,且满足(a-c)⊥b,a⊥c,请加入一个条件,设计问题.

图6

4)进阶提升

通过图7可知,过圆心时有最大值.

图7

图8

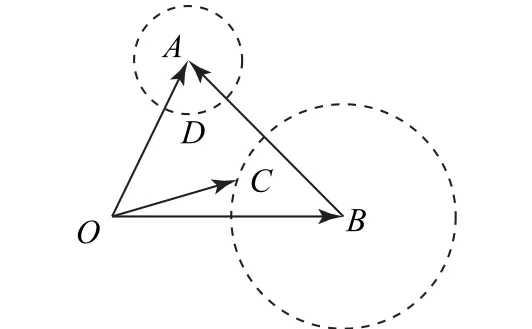
图9

图10

图11

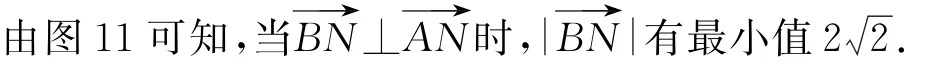
设计意图 以一个基础模型切入,通过不断变化题目条件,培养学生举一反三的能力;不断丰富题目条件,层层深入,拓宽学生解决向量问题时的思路,学会用几何的视角思考向量问题.

3 课堂总结

为了更加突出微专题课程的课堂教学思路,可以通过框架图的形式厘清课堂脉络,以本节课为例,可板书以下框架图(如图13).

图13

4 小结

本文研究的问题是在微专题教学模式下,培养学生在解决平面向量问题时的几何思路.

通过教学实践,在微专题教学模式下进行教学需要注意:选择的问题应该具有典型性,通过变换和丰富题目条件,培养学生举一反三的能力;几何方法在解决平面向量问题时,可以进行推广和一般化,帮助学生在解决问题时做到深入浅出;在组织和培养学生的解题能力时可以按照问题串的方式进行展开,归纳和总结解决数学问题的方法.

总而言之,微专题教学模式在深化学生解决问题的能力时可以起到针对性的效果,教师需要结合教学实践,在课题的选择和组织展开上不断钻研和总结,真正提高学生的数学素养.