巧用特殊函数解与抽象函数相关的问题
——2022年新高考卷一类选择题解法
张 军
(辽宁省大连市第二十四中学)
函数是高中数学教学内容的重点与难点,也是培养学生数学抽象、数学运算、逻辑推理等核心素养的重要载体.抽象函数因为没有函数解析式,可以多方面考查函数的定义域、值域、单调性、奇偶性、周期性等内容,所以与抽象函数相关的问题是现今各类考试的考查热点,又因其对学生的能力要求比较高,也是学生解答的难点.本文力求从函数的运算性质出发,构造符合函数性质的模型,化抽象函数为特殊函数,从而快速准确地解决问题.
所谓抽象函数,是指没有给出函数解析式,但给出了函数所具备的部分性质或者运算法则的函数.与抽象函数相关的问题具有题设抽象、构思新颖、综合程度高等特点,是很多学生在学习函数时的一大难点.大多数学生在解题时往往无从下手,但是如果我们能够根据题设所给的抽象函数性质,通过联想与类比的方式,找到函数模型,就能够化抽象为具体,顺利地解决问题.下面结合2022年新高考Ⅰ卷和新高考Ⅱ卷的两道选择题来进行解答,并对一些常见函数模型进行概括.
1 真题呈现


2 常规解法
2.1 例1解法1
因为f(x+y)+f(x-y)=f(x)f(y),令x=1,y=0,可得2f(1)=f(1)f(0),结合f(1)=1,则f(0)=2.令x=0,可得f(y)+f(-y)=2f(y),即f(y)=f(-y),所以函数f(x)为偶函数.令y=1,可得f(x+1)+f(x-1)=f(x)f(1)=f(x),则有f(x+2)+f(x)=f(x+1),从而可知
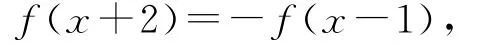
将x替换成x-3得f(x-1)=-f(x-4),故
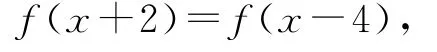
即f(x)=f(x+6),所以函数f(x)的一个周期为6.因为
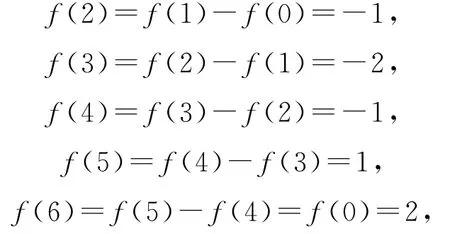
所以f(1)+f(2)+…+f(6)=0.由于22除以6余4,所以

2.2 例2解法1


若函数f(x)满足题设条件,则函数f(x)+C(C为常数)也满足题设条件,所以无法确定f(x)的函数值,故A 错误.
综上,选BC.
3 构造特殊函数求解
3.1 例1解法2
由f(x+y)+f(x-y)=f(x)f(y),可令f(x)=Acosωx(A·ω≠0),则由

故选A.
3.2 例2解法2
引理 若f(a+x)=f(a-x),f(b+x)=-f(b-x),(a≠b),则4(a-b)是函数f(x)的一个周期.
证明 因为
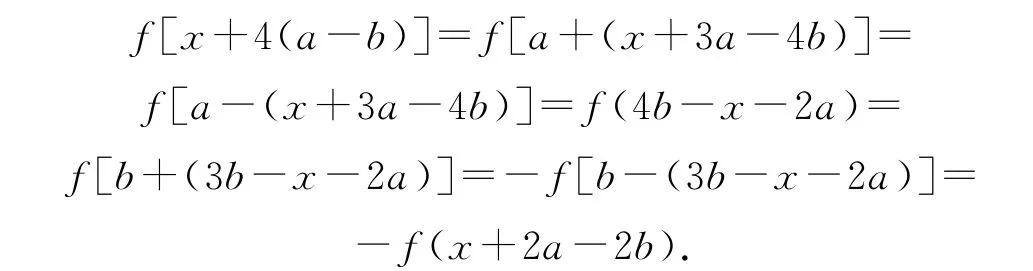
又因为
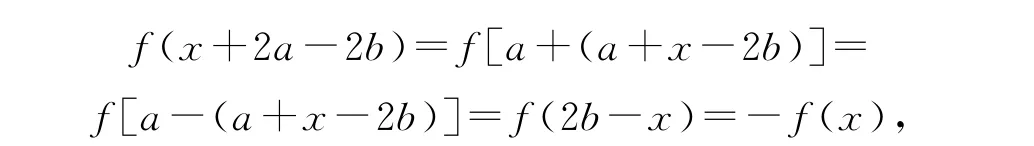
所以f[x+4(a-b)]=f(x),故4(a-b)是函数f(x)的一个周期.

4 常见函数运算法则可构造特殊函数模型
1)若f(x+y)=f(x)+f(y)+b,则可构造f(x)=kx-b.特别地,当f(x)+f(y)=f(x+y)时,可构造f(x)=kx.
2)若f(x+y)=f(x)+f(y)+2axy-c,则可构造f(x)=ax2+bx+c.
3)若f(x+y)=f(x)f(y),则可构造f(x)=ax(a>0且a≠1).
4)若f(xy)=f(x)+f(y)(xy≠0),则可构造f(x)=loga|x|(a>0且a≠1).
5)若f(x+y)+f(x-y)=2f(x)f(y),则可构造f(x)=cosωx.
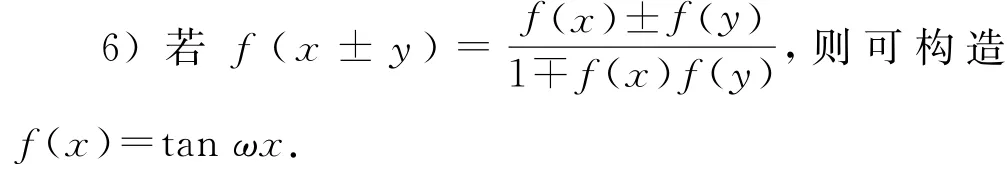
可以看出,如果能够根据抽象函数的运算性质找到函数模型,把抽象函数问题具体化,就能够很容易地破解此类问题.
链接练习
1.已知函数f(x)对任意实数x,y,均有f(x+y)=f(x)+f(y),且当x>0时,f(x)>0,f(1)=2,则函数f(x)在区间[-2,1]上的最小值为_________.
2.已知函数f(x)对任意x,y∈R,满足f(x+y)=f(x)+f(y)-2,且当x>0 时,f(x)>2,若f(3)=5,则f(a2-2a-2)<3的解集为_________.

链接练习参考答案
1.由题意,可取f(x)=2x,则x=-2时,f(x)有最小值为-4.
2.由题意,可取f(x)=x+2,则由f(a2-2a-2)<3可推出a2-2a-3<0,解得-1<a<3,所以不等式的解集为(-1,3).


