赏析数学核心素养视角下一道高考导数真题
苏吉超
(安徽省亳州市第二完全中学)
导数试题多为高考试题中的压轴试题,主要涉及利用导数研究函数的单调性、极值和最值,探究曲线的切线,证明不等式等.此类试题注重考查学生的分类讨论思想、运算求解能力和推理论证能力.
母题 (2021年全国乙卷文21)已知函数

(1)讨论f(x)的单调性;
(2)求曲线y=f(x)过坐标原点的切线与曲线y=f(x)的公共点的坐标.
分析 (1)对函数f(x)求导,讨论导函数与零的关系,进而得出f(x)的单调性情况.
(2)先设出切点,表示出切线方程,根据切线过原点,可求得切线方程,将切线方程与曲线y=f(x)联立,即可求得公共点的坐标.
解 (1)对f(x)求导得f′(x)=3x2-2x+a,则导函数的判别式为Δ=4-12a.

令f′(x)>0,解得x<x1或x>x2,令f′(x)<0,解得x1<x<x2,所以f(x)在(-∞,x1),(x2,+∞)上单调递增,在(x1,x2)上单调递减.


所以切线方程为

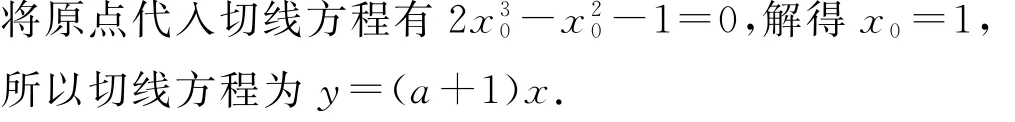
令x3-x2+ax+1=(a+1)x,即x3-x2-x+1=0,解得x=1或-1,所以曲线y=f(x)过坐标原点的切线与曲线y=f(x)的公共点的坐标为(1,a+1)和(-1,-a-1).
【数学建模】本题所涉及的模型主要有两个:一是利用导数研究函数的单调性问题,这里需要学生能够根据所给函数的导数,合理地将所求问题转化为求解二次函数问题,解题的难点在于分类讨论思想的应用.二是导数的几何意义模型,这里需要关注所求切线是“过某点”还是“在某点”,以防掉入试题陷阱.
【数学运算】导数试题的显著特点就在于运算量较大,学生不仅要能够正确求出所给函数的导函数,还要能够根据切线方程的求解方法列出方程,并且能够正确化简.
【逻辑推理】在此问题的求解过程中要能够正确进行分类讨论,根据判别式进行正确的分类讨论,再依据分类的标准求解所给函数的单调区间.
【数学抽象】这里涉及了一个过指定点的切线问题,相比于以往的这类问题,考查角度不同,此题一反常态,不是直接考查切线方程的求法,而是求过指定点的切线与曲线的交点坐标.
【空间想象】在解决函数的单调区间问题时,学生要具备一定的想象能力和作图能力,能够正确作出二次函数的图像是第(1)问求解的保障.同时,对于第(2)问的求解,如果能够正确作出草图,也会使得问题更加直观.
为了更好地对三次函数背景下的导数试题进行求解,下面给出两道数学试题.
练习1 已知三次函数f(x)=x3+ax2-6x+b,a,b∈R,若函数f(x)的图像在x=1处的切线方程为12x+2y-1=0.
(1)求函数f(x)的解析式;
(2)求函数f(x)的极小值;
(3)若存在x∈(0,+∞),使得3lnx≥f′(x)+|2m-1|成立,求实数m的取值范围.
分析 (1)求出函数的导数,利用导数的几何意义求出a,求出切点坐标,代入函数的解析式,求出b,然后可得函数的解析式.
(2)利用导数求出f(x)的单调性即可.
(3)令g(x)=3lnx-f′(x),再利用导数求出g(x)的最大值,然后转化不等式求出m的范围.
解 (1)因为f′(x)=3x2+2ax-6,直线12x+2y-1=0的斜率为-6,所以f′(1)=-6,所以

(2)f′(x)=3x2-3x-6,由f′(x)=3x2-3x-6=0,可得x=2或-1.
由f′(x)<0,可得-1<x<2,由f′(x)>0,可得x<-1或x>2,所以f(x)在(-1,2)上单调递减,f(x)在(-∞,-1)和(2,+∞)上单调递增,所以f(x)的极小值为f(2)=-9.
(3)令g(x)=3lnx-f′(x)(x>0),则

所以

练习2 (2022年北京卷20)已知函数
f(x)=exln(1+x).
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)设g(x)=f′(x),讨论函数g(x)在[0,+∞)上的单调性;
(3)证明:对任意的s,t∈(0,+∞),有
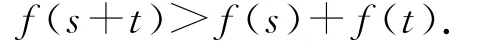
分析 (1)考查求切线方程,只需求出导函数,再求出过点(0,f(0))的切线斜率,按照求直线方程的点斜式求解即可.
(2)引入辅助函数,通过辅助函数的单调性求原函数的单调性.
(3)构造函数,通过求函数的单调性证明不等式.
解 (1)因为f(0)=0,所以切点坐标为(0,0).

所以h(x)在[0,+∞)上单调递增,所以

所以g′(x)>0在[0,+∞)上恒成立,所以g(x)在[0,+∞)上单调递增.
(3)原不等式等价于

令m(x)=f(x+t)-f(x)(x≥0,t>0),即证m(x)>m(0),因为
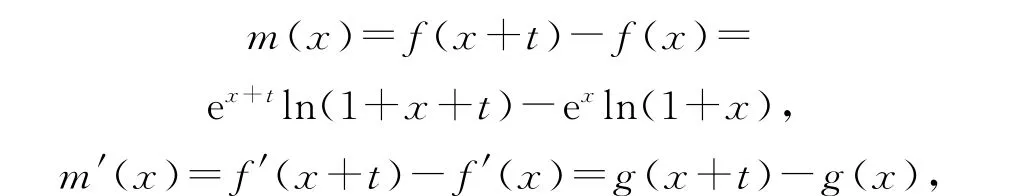
由(2)可知g(x)在[0,+∞)上单调递增,则

则m′(x)>0,所以m(x)在(0,+∞)上单调递增,又因为x≥0,t>0,所以m(x)>m(0),故命题得证.

