对2022年新高考Ⅰ卷第12题的解法探究与推广应用

朱少卿 李雪芳

(广东省佛山市高明区第一中学)

1 题目呈现及解析

2 问题探究

由函数f(x)的图像关于直线x＝a对称可得f(a＋x)＝f(a-x),两边分别求导得f′(a＋x)＝-f′(a-x),即g(a＋x)＋g(a-x)＝0,所以函数g(x)的图像关于点(a,0)对称且g(a)＝0.因为g(2a＋x)＋g(-x)＝0,g(2b＋x)＝g(-x),所以g(2a＋x)＋g(2b＋x)＝0,将x换为x-2a＋2b,则g(2b＋x)＋g(4b-2a＋x)＝0,故g(4b-2a＋x)＝g(2a＋x),所以g(4b-4a＋x)＝g(x),函数g(x)为周期函数且周期T＝4|a-b|.

由函数g(x)的图像关于直线x＝b对称可得g(b＋x)＝g(b-x),构造函数F(x)＝f(b＋x)＋f(b-x),显然F′(x)＝f′(b＋x)-f′(b-x)＝g(b＋x)-g(b-x)＝0,所以F(x)≡c(c为常数,令x＝0,则c＝2f(b)),所以f(b＋x)＋f(b-x)＝2f(b),函数f(x)的图像关于点(b,f(b))对称,函数f(x)为周期函数且周期T＝4|a-b|.

结论1 函数f(x)及其导函数f′(x)的定义域均为R,若f(x)和f′(x)的图像分别关于直线x＝a和x＝b对称,那么f(x)和f′(x)的图像分别关于点(b,f(b))和点(a,0)对称且f′(a)＝0,函数f(x)和f′(x)均为周期函数且周期T＝4|a-b|.

由探究1可知,函数g(x)的图像关于点(a,0)对称且g(a)＝0,因为g(2a＋x)＋g(-x)＝0,g(2b＋x)＋g(-x)＝0,所以g(2a＋x)＝g(2b＋x),所以g(2a-2b＋x)＝g(x),函数g(x)为周期函数且周期T＝2|a-b|.构造函数F(x)＝f(b＋x)-f(bx),则F′(x)＝f′(b＋x)＋f′(b-x)＝g(b＋x)＋g(b-x),因为g(b＋x)＋g(b-x)＝0,即F′(x)＝0,所以F(x)≡c(c为常数,令x＝0,则c＝0),所以f(b＋x)＝f(b-x),函数f(x)图像关于直线x＝b对称,函数f(x)为周期函数且周期T＝2|a-b|.

结论2 函数f(x)及其导函数f′(x)的定义域均为R,若f(x)和f′(x)的图像分别关于直线x＝a和点(b,0)对称,那么f(x)和f′(x)的图像分别关于直线x＝b和点(a,0)对称且f′(a)＝0,函数f(x)和f′(x)均为周期函数且周期T＝2|a-b|.

探究3 若将结论2中的“f′(x)的图像关于点(b,0)对称”改为“f′(x)的图像关于点(b,t)(t≠0)对称”,其他条件不变,函数f(x)的图像是否关于直线x＝b对称?

由函数f(x)的图像关于点(a,0)对称,可得

所以函数g(x)的图像关于直线x＝a对称,由探究2可知函数g(x)为周期函数且周期T＝2|a-b|.由探究1可知,函数f(x)图像关于点(b,f(b))对称,函数f(x)为周期函数且周期T＝2|a-b|.

结论3 函数f(x)及其导函数f′(x)的定义域均为R,若f(x)和f′(x)的图像分别关于点(a,0)和直线x＝b对称,那么f(x)和f′(x)的图像分别关于点(b,f(b))和直线x＝a对称,函数f(x)和f′(x)均为周期函数且周期T＝2|a-b|.

结论4 函数f(x)及其导函数f′(x)的定义域均为R,若f(x)和数f′(x)的图像分别关于点(a,0)和点(b,0)对称,那么f(x)和f′(x)的图像分别关于直线x＝b和直线x＝a对称,函数f(x)和f′(x)均为周期函数且周期T＝4|a-b|.

结论5 可导函数f(x)的图像关于点(a,f(a))对称的充要条件是其导函数f′(x)的图像关于直线x＝a对称,可导函数f(x)的图像关于直线x＝a对称的充要条件是其导函数f′(x)的图像关于点(a,0)对称.

结论6 若函数f(x)的图像关于点(a,c)成中心对称,关于直线x＝b成轴对称,则f(x)是周期函数且周期T＝4|a-b|;若函数f(x)的图像分别关于点(a,c)和点(b,c)成中心对称,则函数f(x)是周期函数且周期T＝2|a-b|;若函数f(x)的图像分别关于直线x＝a和直线x＝b成轴对称,则函数f(x)是周期函数且周期T＝2|a-b|.

3 推广应用

例1 设函数f(x)＝x3-(a-1)x2＋ax-2,若f(x＋1)为奇函数,则a的值是________.

因为f(x＋1)为奇函数,所以f(x)的图像关于点(1,0)对称,根据结论3或结论4可知其导函数f′(x)的图像关于直线x＝1对称.

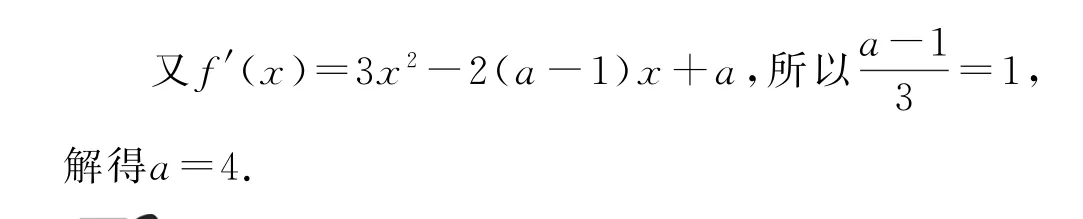
例2 (2013年新课标Ⅱ卷理10、文11)已知函数f(x)＝x3＋ax2＋bx＋c,下列结论中错误的是( ).

A.∃x0∈R,f(x0)＝0

B.函数y＝f(x)的图像是中心对称图形

C.若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)上单调递减

D.若x0是f(x)的极值点,则f′(x0)＝0

对于选项C,由于f′(x)＝3x2＋2ax＋b的图像是开口向上的二次函数,若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)上不单调(先增后减),故选项C错误.

对于选项D,若x0是f(x)的极值点,根据导数的意义可知f′(x0)＝0,故选项D 正确.

综上,选C.