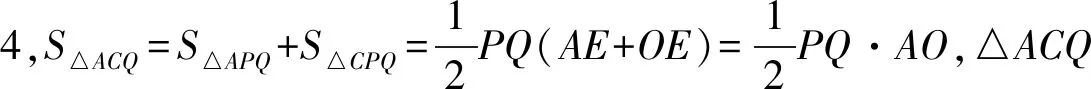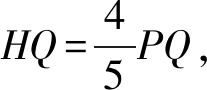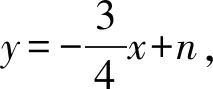单元整体教学视角下的复习课教学探究
——以“二次函数的图象和性质”为例
裴 姣
(江苏省宜兴外国语学校,江苏无锡,214200)
单元复习课中知识以何种形式呈现,能让概念复习不再是枯燥的无效重复,能让学生思维在巩固中落实提升?课前教师有必要把单元内容进行整体规划,优化整合,在情境中把问题联系结合起来,通过情景式问题串带领学生回忆相关知识,让学生在一个个问题的关联中感受数学的整体性,感悟知识点之间的相互联系,让知识生长起来.通过学生自我整理、归纳知识,构建知识体系,达成学生对于知识的理解更透彻,达成学生思维能力和数学素养有效提升.下面,笔者以苏科版九年级下册第五章“二次函数”的单元复习教学为例,谈谈基于整体教学视角下,单元复习教学的实践与思考.
1 教材内容分析
1.1 内容分析
二次函数是初中数学“数与代数”部分的内容,教科书把“代数式—方程—不等式—函数”作为这部分课程内容的主干[1],它们自成体系,都沿用了“由实际问题到数学模型—研究数学问题(图象、性质)—解决实际问题”的学习思路,“数与代数”学法是相通的.从函数板块分析,二次函数是学生在学习一次函数、反比例函数后又一次接触到的重要模型,放最后出现,从知识和思维层面,都表明它对学生能力要求更高,综合性更强,在各地中考试卷中,二次函数常以压轴题的形式出现.二次函数的相关知识结构如图1所示.

图1
1.2 复习目标
(1) 通过对二次函数知识的回忆和梳理,巩固二次函数的概念、函数表达式、待定系数法、图象和性质,由抛物线和抛物线上的点,感悟确定的数量与图形直观间的紧密联系.
(2) 通过从函数的视角看一元二次方程(不等式),明确二次函数与一元二次方程(不等式)、一次函数的关系,能用二次函数模型解决简单的实际生活问题,提高数学抽象思维能力.
(3) 引导学生在归纳整理知识和探究问题的过程中,体会函数学习的方法,感悟模型思想、数形结合思想.
1.3 复习重点、难点
重点:二次函数的表达式、图象和性质.
难点:结合图象解题,应用二次函数性质解决问题.
1.4 教学准备
复习二次函数相关知识点,重难点,列出存在的问题,把知识点整理成文字、表格、结构图或思维导图,小组成员开展互评,在课前展示优秀作业.
2 由点入手,“对称”指路
例1见表1,已知二次函数图象上部分点的横坐标x和纵坐标y对应的值,
问题1:观察表1,你能获得哪些信息?

表1
鼓励学生仔细观察数值特征,大胆发表看法.经过充分观察和思考后,结合学生的回答和教师引导,完成表2的问题.
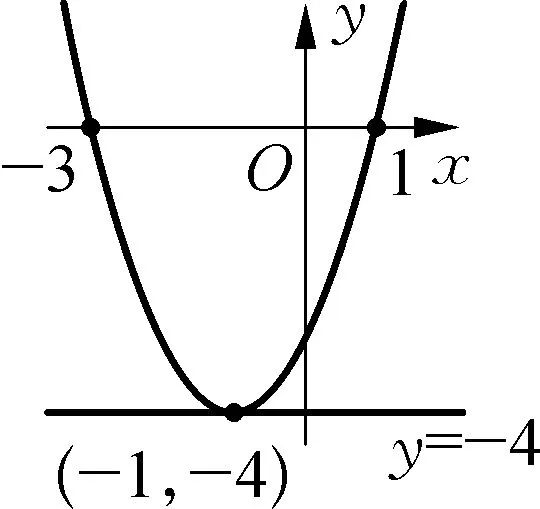
思路启发:因为x=-2和x=0时函数值相等都是-3,根据二次函数的对称性,确定对称轴是直线x=-1,表格数据知(-1,-4)即为顶点坐标.再由对称性知点(1,0)关于直线x=-1的对称点(-3,0)为图象与x轴的另一交点.随着x的值从左到右逐渐增大,对应的函数值y先减小后增大,确定开口向上,当x=-1时,函数值最小是-4.
问题2:已知点(-2.5,y1),(-0.5,y2),(2,y3)是表1中对应抛物线图象上的三个点,则y1、y2、y3之间的大小关系是.
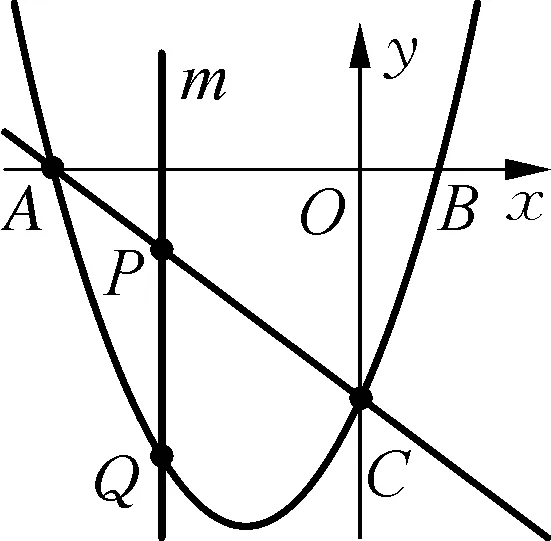
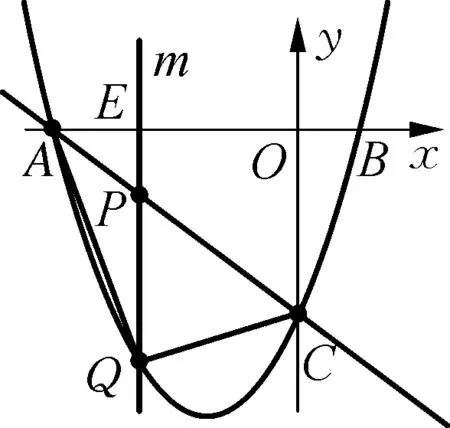
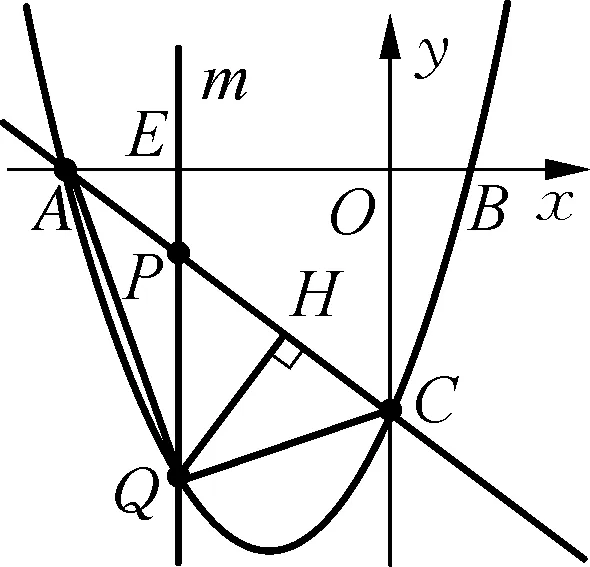
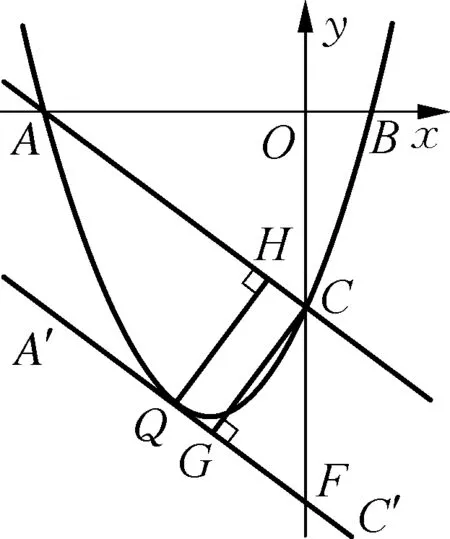
思路启发:如图2,把(-2.5,y1)转化为它关于对称轴的对称点(0.5,y1),这样三个点都在对称轴的右侧,根据增减性知y随x的增大而增大,因为-0.5<0.5<2,所以y2 图2 设计意图:抛物线是轴对称图形,它不仅充盈和谐之美,还显露数学的灵活与精巧.运用对称的思想来观察点、转化点,灵活捕捉、落实对称,不仅简化大量复杂的运算,还能开辟出新的解题路径. 问题3:请你求出表1对应的函数表达式.你有几种方法? 让学生动笔写下过程,再一起交流方法. 思路启发:二次函数表达式有三种形式,若已知顶点,可设函数表达式为y=a(x+1)2-4(a≠0);已知三个点,可设函数表达式为y=ax2+bx+c(a≠0);已知图象与x轴的交点,可设函数表达式为y=a(x+3)(x-1)(a≠0),表达式中有几个待定系数,就代入几个已知点求出这个待定系数.三个表达式形式虽不同,但实质是同一个式子. 设计意图:确定一次函数、反比例函数、二次函数的表达式,都是待定系数法,足见待定系数法在求函数表达式中的重要作用.通过观察列出的方程(组),让学生体会变量和常量的区别,感受方程(组)与函数的内在关联. 问题4:三个点一定能确定二次函数表达式吗? (1) 已知三点(-2,-3),(-2,-2),(0,0);(2) 已知三点(-2,-2),(0,0),(1,1). 思路启发:留出充分观察思考的时间,鼓励学生说出看法.问题4中第一问不能,因为两个点(-2,-3),(-2,-2)横坐标相同,这与函数概念“两个变量x与y,对于x的每一个值,都有唯一的y的值与它对应”不符;第(2)问也不能,因为三点在一直线上. 设计意图:聚点成线,线的形状如何,要由点的位置和点的变化趋势来决定,在不明确函数类型的情况下,生搬硬套是对函数概念的混淆,碰到这类问题可以按照:描点——观察猜想——连线——写出表达式的步骤处理. 问题5:如图3,是表1中对应的抛物线图象,(1) 如何平移这个抛物线,使其顶点过原点?(2) 如何左右平移这个抛物线,使其图象过原点?(3) 如何平移这个抛物线,使其顶点正好落在坐标轴上?写出函数表达式. 图3 思路启发:确定抛物线平移的方向和距离,抓住平移前后对应点的关系展开,(1)(2)两问终点为坐标原点,只要找出特殊点平移前的位置即可,第(1)问自然是顶点,第(2)问看抛物线与x轴的两个交点,第(3)问要注意x轴和y轴都是坐标轴,分两种情况讨论向右平移1个单位或向上平移4个单位,由于坐标轴上的点有无数个,因此抛物线平移后顶点的位置不能确定,故有无数种平移方式,函数表达式可根据二次项系数a和顶点具体位置来写. 问题6:把如图3的抛物线沿x轴或y轴翻折,分别写出翻折后的抛物线表达式. 问题7:把如图3的抛物线绕原点旋转180°,写出旋转后的抛物线表达式. 思路启发:如图4,图形变换的本质,图形的形状和大小不变,只有位置改变.形状取决于|a|,位置看特殊点与开口方向,通常知道a和顶点就能写出函数表达式. 图4 设计意图:研究抛物线先研究点,由关键的点来确定整体情况,从具体到抽象符合认知规律,抓住图形变换前后变与不变的关系,变化的量变成了什么,让学生先定点再画线,后写出表达式,感悟“以形助数”的数形结合思想. 问题8:如图3,结合图象,(1) 直接写出方程x2+2x-3=0的解; 思路启发:从函数的角度出发,联系一元二次方程与二次函数的关系,方程ax2+bx+c=0(a≠0)的根的情况就是二次函数y=ax2+bx+c(a≠0)与x轴交点的情况,二次函数与x轴交点的横坐标就是一元二次方程的两个实数根,观察函数图象知,方程的解为:x1=-3,x2=1. (2) 写出方程x2+2x-3=-4的解; 思路启发:如图5,从函数角度看这个方程,方程的解的情况是函数y=x2+2x-3与直线y=-4的交点情况,因为抛物线与直线只有唯一交点,所以方程有两个相等实数根.观察函数图象知,方程的解为:x1=x2=-1. 图5 (3) 探究方程x2+2x-3=k(k为常数)的根的情况; 思路启发:如图6,与第(2)问中不同的是等式右边从-4变为k,鉴于k的不确定,直线y=k是一组垂直于y轴的动直线,结合上一题的经验,二次方程的解的情况取决于二次函数和动直线交点的情况,分k<-4,k=-4,k>-4三种情况展开讨论. 图6 (4) 探究方程x2+2x-3=x-1的根的情况; 思路启发:如图7,一元二次方程的根的情况是函数y=x2+2x-3与直线y=x-1的交点情况,方程的根是两个交点的横坐标,画出函数图象,由图象知,方程的解为:x1=-2,x2=1. 图7 (5) 已知不等式x2+2x-3>x-1,求x的取值范围. 思路启发:从函数角度审视不等式,令y1=x2+2x-3,y2=x-1,即求y1>y2时x的取值范围,要找在x相同情况下,y1的函数值大于y2的函数值,反映在图象上即找出当x为同一数值时,二次函数图象在一次函数图象的上方的部分,结合图象知,x的取值范围为:x<-2或x>1. 设计意图:把一元二次方程(不等式)处理成两个函数间相关问题,体现数学知识相辅相成,相互关联,具有整体结构,也体现数学思维的灵活性,从不同的角度去思考,能收获新的方法.把一元二次方程(不等式)转化为函数问题,观察函数图象,从函数的交点,函数值的比较,自变量(函数值)范围等处去研究,直观明了,实现“化数为形,以形助数”,让学生很好地感悟到数形结合、转化等重要思想方法. 例2如图8,已知抛物线过A(-4,0),B(1,0),C(0,-3),作直线AC,点P是线段AC上一动点(不与点A,C重合),过点P作x轴的垂线m,与抛物线交于点Q, 图8 问题9:求线段PQ的最大值. 思路启发:点P、Q都是动点,PQ是垂直于x轴的一组动线段,任何位置P、Q的横坐标满足相等,PQ的长度就是两点纵坐标之差的绝对值,结合图象,即PQ=yp-yQ,用代数式表示出PQ的长度,转化为求二次三项式的最值,用配方法或顶点公式求出最值. 设计意图:线段的长度就是两端点之间的距离,我们知道,在平面直角坐标系中,有两点坐标就能算出两点间的距离,结合二次函数和一次函数图象上动点的坐标规律,表示出线段长度的代数式模型,运用函数知识求出最值.引导学生经历运用解析法求最值问题的过程,感受数与形的紧密联系及模型思想. 问题10:如图9,连接AQ,CQ,求△ACQ面积的最大值. 图9 设计意图:割补法是处理面积问题的一般方法,在二次函数中同样适用,可从“割”或“补”的角度去处理图形,把问题中的三角形面积转化为新图形面积的和或差,以此畅通思路,找到可行的解题方法.在平面直角坐标系中,铅垂线段和水平线段是更为特殊的线段,要充分把握住这些线段,表示出三角形的底和高,复杂图形的组成还是基本的点和线,要善于捕捉,用这些特殊作用的点和线去表示题中的未知量.通过分析探究过程,引导学生体会数学转化的作用,培养学生分析问题的能力. 问题11:如图10,作QH⊥AC于点H,垂足为点H,求线段QH的最大值. 图10 设计意图:“斜化直”是平面直角坐标系中转换线段的有效方法,通过相似三角形或锐角三角函数找出线段间的数量关系,把线段转换为铅垂线段和水平线段更易于处理和表示,培养学生大胆构造,缜密思考,灵活运用的思维习惯和能力. 一题多解(一):由三角形入手,把QH看成△ACQ中AC边上的高,底边AC是定值5,当高最大时,面积最大,把求QH的最大值转化为问题10中求△ACQ面积的最大值. 图11 知识的复习,也要关注“知识链”的产生、生长过程.本复习课例,从创设问题情境入手,把二次函数纷繁零碎的知识点整合到问题串中,通过对问题的探究,帮助学生巩固基础知识,对知识归类整合,把点状知识聚集为块状知识,进而内化建构成知识体系.在知识巩固的过程中,注意对学生思维能力的培养,通过问题串把相近思维点或相同方法的问题放一起,更易于学生掌握数学思想方法,感悟变式题的通性通法,提升思维能力和核心素养.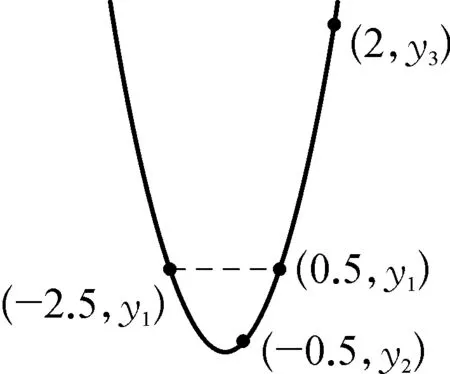
2 观察图象,数形结合
2.1 图形变换

2.2 二次函数与一元二次方程(不等式)


3 知识整合,思维提升