基于深度学习的高中数学课堂教学策略研究——以《余弦定理》为例

高敬飞,孙向辰

(哈尔滨师范大学教师教育学院，黑龙江哈尔滨，150000)

目前，新课程改革如火如荼，各省的高中数学课程开始使用新教材，与之配套的课堂教学方法需要新的理念进行指导.深度学习的理论与核心素养目标非常契合，可以借助深度学习理论指导新的高中数学课堂教学.在2019人教A版高中数学教材中，《余弦定理》一节课的位置调整到了必修第二册第六章“平面向量及其应用”一章.这一调整，彰显了新课程重视数学应用性的理念.

1 核心概念界定

关于深度学习，有着多视角的理解.

郭华教授认为，所谓深度学习，就是指在教师引领下，学生围绕着具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义学习的过程.[1]

钟启泉教授认为，“深度学习”是指“学习者能动地参与教学的总称”，亦即“通过学习者能动地学习，旨在培育囊括了认知性·伦理性·社会性能力，以及教养·知识·体验在内的通用能力”.[2]

基于以上观点，在高中数学教学中，本文将深度学习的概念界定如下：深度学习是指在教师的指导下，学生在具体的情境中，围绕本节课的学习目标，经历知识的形成过程，掌握数学知识的本质，建立新旧知识的联系，培养数学思维和用数学方法解决问题的能力，发展数学核心素养的学习过程.

2 高中数学的深度学习课堂教学设计策略

2.1 明确深度学习的教学目标

教师作为课堂教学的主导者，需要结合普通高中数学课程标准、本节课的学习任务、学生的实际情况，制定合理的教学目标.借助深度学习理论，教师要摒弃以往“碎片化”教学的理念，明确在本节课中，学生需要“掌握哪些知识”“如何掌握这些知识”“新旧知识有哪些联系”，将本节课内容与学生已有的知识融合成有机整体.教学目标是指导课堂活动的关键所在，教师制定的教学目标需要容易落地，掷地有声.

2.2 创设基于学生认知的现实问题情境

在实际高中数学课堂中，学生已经经历过义务教育阶段的数学课程学习，在学习数学过程中形成了一定的方法和认知基础.部分同学认为数学课程难度很大，在学习高中数学课程之前就已经产生畏难情绪.而心理学研究表明，学生熟悉的真实问题情境，能够激起学生的研究兴趣，而且学生对熟悉的内容接受程度较高.深度学习理论指导教师去创设合理的问题情境，形成认知冲突，引导学生尝试用数学眼光看世界，用数学语言表达问题，用数学方法解决问题.[3]

2.3 设置基于深度学习的学习活动，探究数学本质

基于深度学习所创设的情境将学生的注意力吸引到将要学习的内容上来.如果整堂课的内容都仅限于有趣、好玩，就失去数学课程的学习数学知识和技能、锻炼数学思维、提升数学核心素养的作用，舍本逐末.因此，教师需要保证数学课程的思想性，在成功将学生注意力和兴趣引导到新知识学习上来后，引导学生思考如何利用已有的知识尽可能“靠近”解决现实问题.具体的策略是：设置具有逻辑性、思想性和方法性的问题串和学习活动，引导学生在解决问题的过程中获得新知，并且引导学生把握新知识的数学本质，建立新旧知识之间的联系.教师设计的问题串和学习活动要让学生的思维充分“外显”，可以利用让学生自我分析、质疑辩论等等方式.

2.4 进行追求深度学习的反思指导

传统的课堂教学虽然强调了反思的重要性，但是教学终结的反思不过是蜻蜓点水的一种点缀而已.进行反思的目的是，希望学生能够回顾数学课堂的经历，品味在数学课堂中有什么收获.当致力于实现真实的深度学习的时候，教师可以把基于数学学科素养的理想的“反思”作为方向目标来设定，进行逆向教学设计.[2]

3 基于深度学习的教学设计

下面以《余弦定理》一节为例进行基于深度学习的教学设计.

3.1 教学目标

(1) 经历把实际问题抽象为数学问题，利用平面向量定量研究三角形两边及其夹角确定第三边的过程，推导余弦定理，体会平面向量的工具性；

(2) 通过定量研究三角形的边角关系，建立全等三角形判定定理，勾股定理与余弦定理的联系，形成新的认知结构；

(3) 通过实例探究余弦定理，并用余弦定理及其推论解决问题，提升数学建模、数学抽象、逻辑推理和数学运算的核心素养.

3.2 教学重难点

(1) 重点：余弦定理及其推论，余弦定理的应用；

(2) 难点：余弦定理的探索证明.

3.3 教学过程

3.3.1 创设情境

问题1如图1，某勘测队测量某一湖面的宽度，但是，湖边地势复杂，于是勘测队员在地势较平缓的地方选择了一个适当的位置C，量出了C到湖边A，B的距离，其中CA=3 km，CB=2 km，并利用经纬仪测出∠ACB=120°，那么，根据上述条件勘测队能否测出湖面AB的宽度？

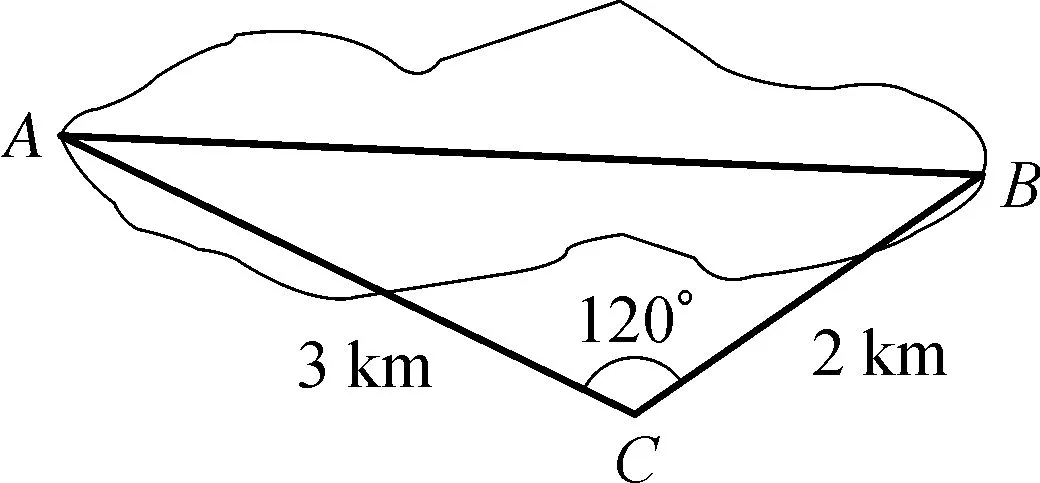
图1

追问1：用题目中的条件，可以确定AB的长度吗？你的理由是？

预设：两边和它们的夹角分别相等的两个三角形全等(SAS)，也就是说，给定两边及其夹角的三角形是唯一确定的.因此，根据题目中的条件，可以确定AB的长度.

设计意图:回忆初中学习的定性研究三角形的边角关系方法，根据判定三角形全等的方法，可以由三角形的三条边、三个角中的某些元素唯一确定三角形的形状，为定量研究这些元素的数量关系做铺垫.

追问2：给定两边及其夹角的三角形是唯一确定的，也就是说三角形的其他边和角都可以利用这两边及其夹角来表示.利用三角形的两边及其夹角求第三边，你有什么方法？

预设：利用向量法.

设计意图:由研究问题的特点，适配平面向量工具的应用条件，引出本节课主要探究方法是向量法.

3.3.2 探索新知

问题2在△ABC中，三个角A，B，C所对的边分别是a，b，c，怎样用a，b和C表示c？

追问1：图2中有哪些要素可以表示为向量？将几何元素用向量表示后，问题转化成了什么？

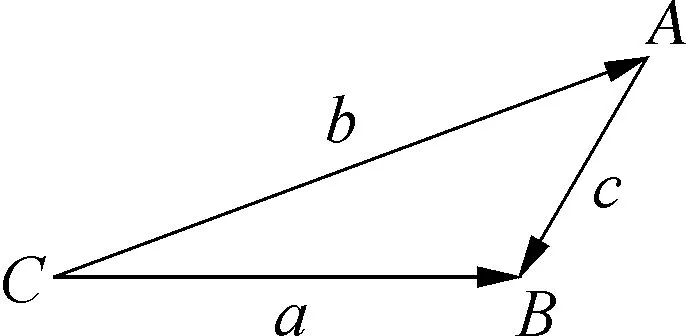
图2

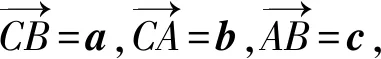
追问2：根据转化后的条件和问题，你认为能利用向量的什么性质去解决呢？

预设：|c|2=c2.

学生活动：请用|a|，|b|和C表示|c|.

|c|2=c·c=(a-b)·(a-b)
=a·a+b·b-2a·b
=a2+b2-2|a||b|cosC.

将向量式转化为几何式，得：

c2=a2+b2-2abcosC.

追问3：如何用已知的边b，c和它们的夹角A表示第三边a？如何用已知的边a，c和它们的夹角B表示第三边b？

预设：a2=b2+c2-2bccosA；b2=a2+c2-2accosB.

余弦定理：三角形中任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.

学生活动：尝试用余弦定理解决问题1.

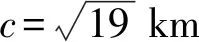
设计意图:将实际问题抽象为数学问题，引导学生利用平面向量解决几何问题的“三步曲”解决该问题，增强学生用数学知识解决实际问题的能力，提升学生的数学建模的核心素养，使学生感受到数学的应用性、逻辑美、对称美.

问题3观察余弦定理的某一个公式，你能否将其进行变形得到其他的结论？

预设：由余弦定理，可以得到如下推论：

设计意图:引导学生深入思考，利用方程思想深入挖掘得到的余弦定理的公式，拓展余弦定理的应用范围.

3.3.3 认知深化

思考1：利用余弦定理，可以解决什么类型的几何问题？

预设：已知三角形的两边及其夹角直接求出第三边.

思考2：利用余弦定理的推论，可以解决什么类型的几何问题？

预设：可以由三角形的三边直接计算出三角形的三个角.

思考3：初中学习的勾股定理指出了三角形中的三边关系，余弦定理指出了三角形的三条边与其中的一个角之间的关系，你能说说这两个定理之间的关系吗？

预设：余弦定理是勾股定理的推广，勾股定理是余弦定理的特例.

思考4：你能用其他方法证明余弦定理吗？课下请同学们继续探究.

设计意图:由一系列问题串引导学生思考，并数学地表达自己的思维过程，在教师的引导下，归纳出用平面向量解决几何问题的一般步骤.通过一系列的追问、学生的批判思考，培养逻辑推理、数学运算的核心素养.将新学的余弦定理与初中学习的全等三角形的判定、勾股定理建立联系，使学生将新旧知识整合，形成新的认知结构，避免“碎片化”的学习.

问题4利用余弦定理及其推论，你认为要求出三角形的三条边、三个角，至少需要几个条件？

预设：至少需要三个条件.

一般地，三角形的三个角A，B，C和它们的对边a，b，c叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫做解三角形.

设计意图:强调余弦定理及其推论的使用条件，明确其能够解决什么样的数学问题，达到应用余弦定理及其推论的目的.

3.4 教学反思

《普通高中数学课程标准(2017年版)》指出，高中数学课程的基本理念是：学生发展为本，立德树人，提升素养；优化课程结构，突出主线，精选内容；把握数学本质，启发思考，改进教学；重视过程评价，聚焦素养提高质量.[4]

3.4.1 更新观念，发挥数学学科的育人价值

基于以上案例，在数学课堂教学中，教师并不是简单地将某个知识点讲授给学生，而是引导学生通过对现实世界的观察，学会数学地观察、表达自己的思维.教师要让学生去做课堂的主人，让学生在课堂中去体会数学知识的发现、归纳、应用的过程，去探究知识的来龙去脉，改变以往唯知识、唯习题的课堂授课模式，发挥数学课堂锻炼逻辑思维、感悟数学之美、培育严谨求实的科学态度的育人价值.

3.4.2 钻研教材，进行深度学习的教学设计

为落实核心素养，进行深度教学，教师需要深入分析教材，研究本节课内容的特点、位置、地位、作用，本节课知识与前后知识的联系、逻辑关系，建立严密的知识系统，保证数学的整体性、系统性，防止碎片化教学.在教学中，创设真实的问题情境，搭建对话交流的平台，让学生真正参与到课堂活动中来.

3.4.3 持续评价，激励学生深度思考

在深度学习的课堂中全方位地把握“教育评价”.诚然，成绩评价是教育评价的一部分，但是，教师在课堂教学中不能仅仅依靠成绩评价.教师在课堂中的对话、提问、交流过程中，都可以及时对学生作出评价，实时激励学生深度参与到课堂活动中来.这对增强学生学习数学的信心具有重要意义.