运用“四环五步”谈初中几何定理教学设计——以《三角形中位线定理》教学为例

梁艳云,涂爱玲,蒋晓云

(1. 广西师范大学附属外国语学校，广西桂林，541004 2. 桂林师范高等专科学校，广西桂林，541199)

1 几何定理教学的内涵

数学是思维的体操，几何是思维的艺术体操.平面几何造就了大量的数学家，初中几何概念与定理构成了初中几何教学的基石，是几何证明与推理最重要的依据.然而，几何定理教学不是简单的、肤浅的、一蹴而就的，几何定理具有抽象、凝练、深刻的特点，它需要思维的深度参与，经历直观感知、分析发现、归纳提炼、猜想论证，从表象走向本质，从孤立建立联系，从特殊归纳一般，从合情演绎逻辑.正因为如此，有人感叹初中数学学习成也几何，败也几何！这是极具挑战性的教学内容，教师在教学过程中，要有明确的目标和清晰的路径，让学生走上学好几何探索智慧之路！

数学课程改革已进入内涵发展时期，核心素养是新一轮课程改革的关键词，具体指学生在日常学习生活中必备的适应终身发展的品格和能力.在几何定理教学中，重视对学生几何直观，空间观念的培养，进一步发展推理能力和模型思想，并将几何定理教学落实到问题解决中去，发展学生的应用意识和创新意识，培养学生思维的灵活性和开阔性，实现浅层识记→简单应用→迁移转化→创造应用的转变.

“探索并证明三角形的中位线定理”是课程标准中专门列出的教学内容，下面本文以此作为初中几何定理教学研究的典型案例，并运用“四环五步”教学模式与路径谈几何定理教学设计.

2 几何定理教学的过程

所谓的“四环五步”，“四环”指教学的四个环节，即“问题导入→新知探究→变式应用→总结升华”[1]；“五步”指几何定理探索的五个步骤，即“动手操作(或素材感知)→观察分析→形成猜想→论证猜想→归纳定理”.

环节1：问题导入

知识科普：通过前面的学习，了解到像三角形、四边形这些基本图形可以通过割补剪拼互相转化.

设计说明：启迪学生在几何学习过程中，运用割补剪拼可以实现三角形、四边形等几何图形的相互转化，为接下来三角形中位线定理的探究埋下伏笔.

环节2：新知探究

第1步：动手操作

问题1如图1①，请你沿中位线EF剪下△AEF后，绕点F旋转180°拼成了如图1②所示图形，试判断它是平行四边形吗？

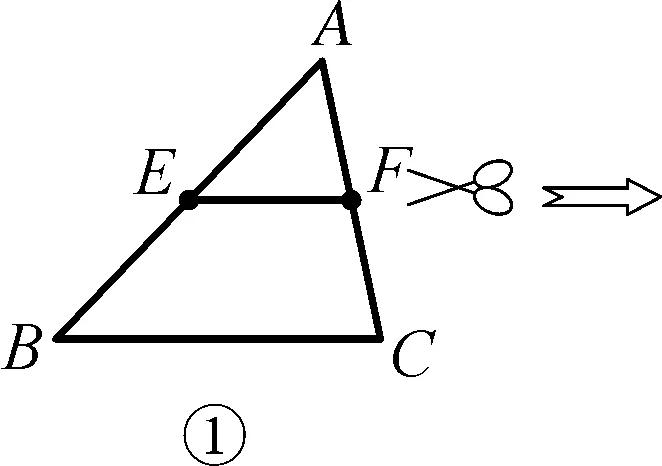
图1

第2步：观察分析

问题2试判断图1②所拼成的图形是平行四边形.

思路点拨：分析E、F、G三点共线→说明所拼图形为四边形→判断四边形BCGE是平行四边形.

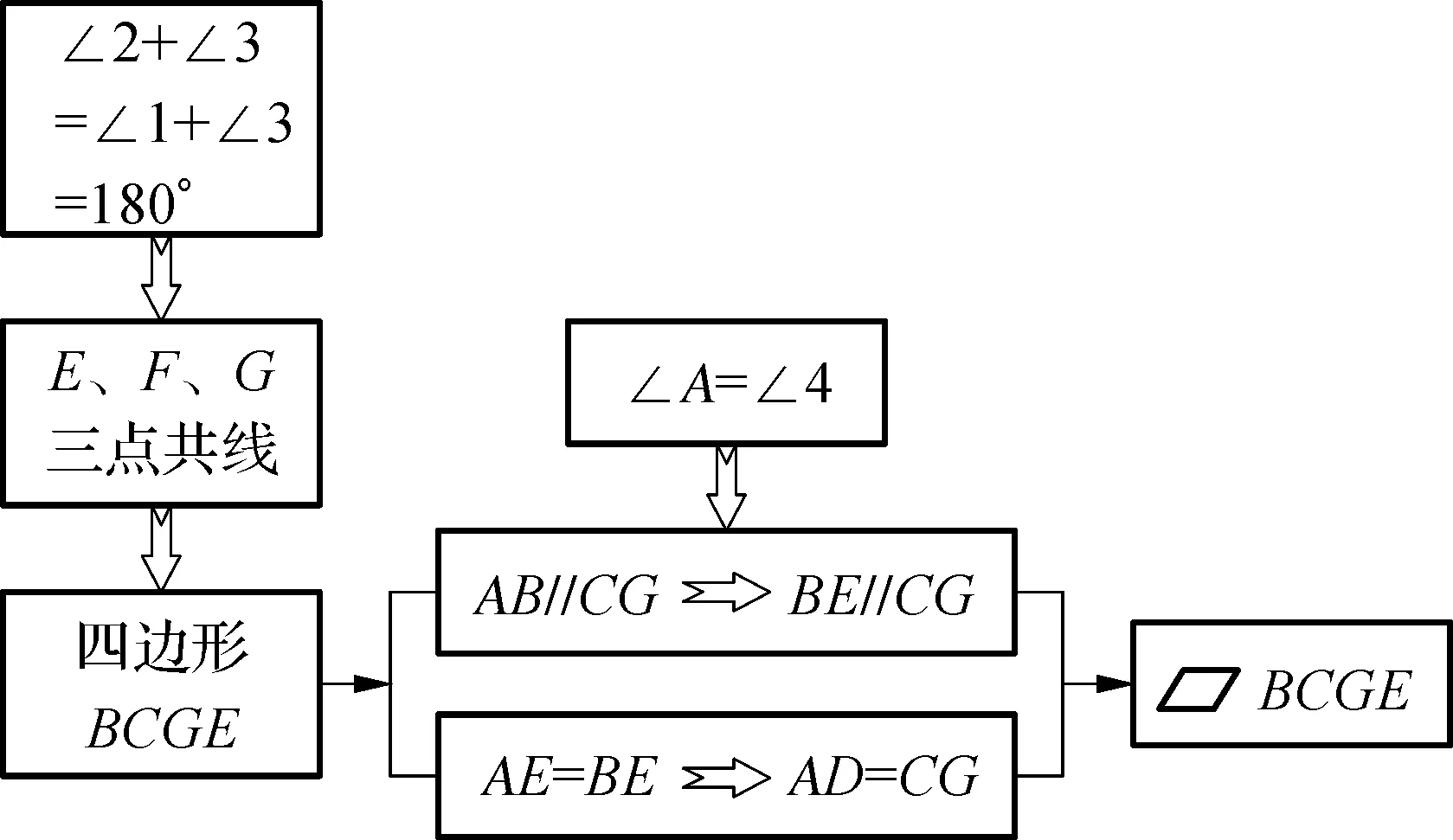
第3步：形成猜想

思路点拨：由平行四边形性质→对边平行且相等→三角形中位线平行第三边且等于第三边的一半.

第4步：论证猜想

问题4求证：三角形中位线平行于第三边且等于第三边的一半.

思路点拨：画图→写已知求证→证明.

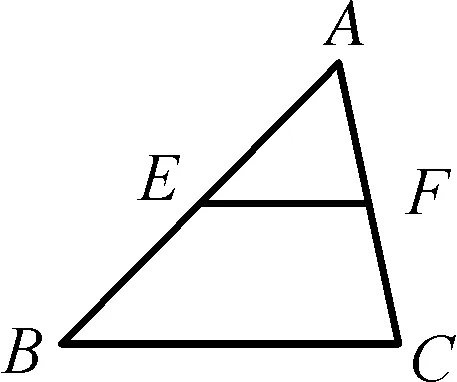
图2

证明思路：如图3，构造△CGF≌△AEF→证明BCGE→结论得证.

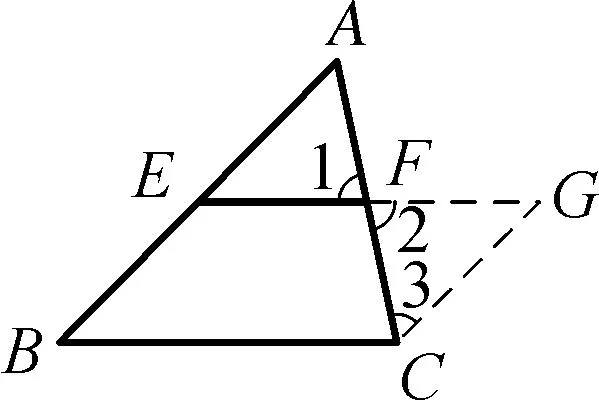
图3

第5步：归纳定理

文字语言：定理：三角形中位线平行于第三边且等于第三边的一半.

符号语言：如图3，∵EF是△ABC的中位线

设计说明：通过图形的旋转剪拼，让学生动态直观的体验定理的探索发现的过程；静态观察拼接后的图形形状，分析图形中的数量与位置关系；动静结合，旧识现新知，提出猜想；回顾探索路径，类比概括，由合情分析转化为严格证明；归纳提炼形成定理，从文字语言、符号语言、图形语言全面认识三角形中位线定理.

环节3：变式应用

问题5如图4，在△ABC中,E、F分别为AB、AC中点.

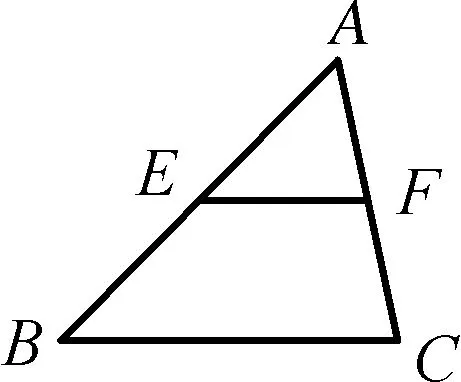
图4

(1) 若EF=5，则BC=；

(2) 若∠AFE=70°，则∠C=.

变式1如图5，在△ABC中，点E、F、G分别为AB、AC、BC中点.

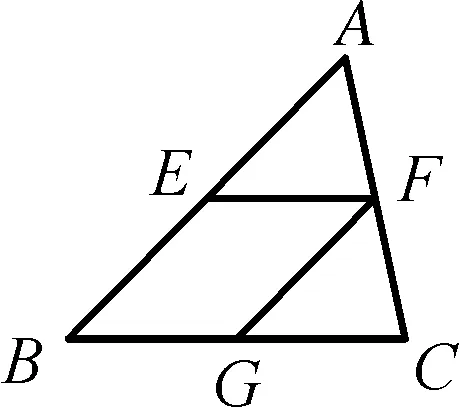
图5

(1) 四边形EBGF的形状是；

(2) 若AB=10，BC=8，四边形EBGF的周长等于.

变式2如图6，点E、F、G是△ABC三边AB、AC、BC的中点.

图6

(1) 图中有个平行四边形；

(2) 图中有对全等三角形；

(3) 若AB=10，BC=8，AC=6，

①C△GFE=；

②S△GFE=.

(4) 若AB=a，BC=b，AC=c，S△ABC=m

①C△GFE=；

②S△GFE=.

变式3如图7，点E、F、G、H是四边形ABCD四边的中点.

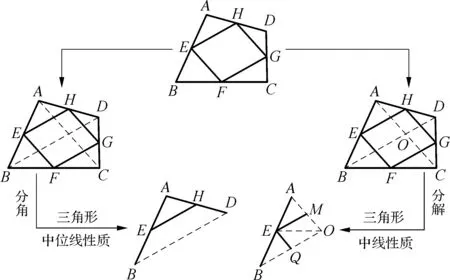
图7

(1) 四边形EFGH的形状；

(2) 若AC=10，BD=12，则C四边形EFGH=；

(3) 若AC=a，BD=b，则C四边形EFGH=；

(4) 若S四边形ABCD=m，则S四边形EFGH=；

(5) 中点四边形的周长、面积分别与原四边形的周长、面积之间存在怎样的数量关系？

拓展：如图8，已知四边形ABCD,请你经过剪拼，使它变为一个平行四边形.

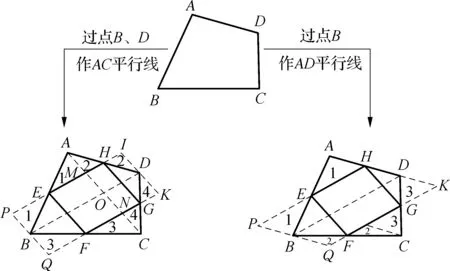
图8

思路点拨：

设计说明：变式应用环节，设计了一组由浅入深，层层递进的变式题组.问题梯度由直接应用→综合应用→构造应用；问题类型由计算线段长度→判断图形形状(平行四边形)→判断图形关系(全等三角形)→计算图形周长→计算图形面积→剪拼平行四边形，涉及到几何研究的图形形状、数量、位置的各个方面，多角度考查三角形中位线；形成两类几何模型，即中点三角形和中点四边形，揭示了其中所蕴含的周长面积的基本数量关系，及特殊图形形状.在拓展中，很巧妙地将三角形中位线定理的探究思路，即旋转剪拼思路运用到解题过程中来，起到了很好的迁移转化的作用.本题组环环相扣，将知识、问题、策略有机融合，逐步渗透培育数学学科核心素养的育人理念.

环节4：总结升华

问题6请同学们回顾并梳理本节的学习内容，谈谈你有哪些收获？还存在哪些疑惑？

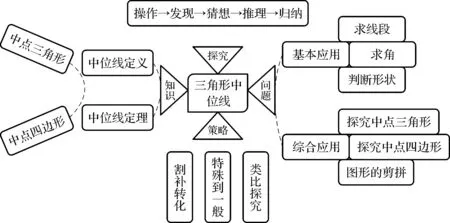
设计说明：引导学生分别从定理探究、核心知识、问题类型、解题策略四个角度，回顾本节课的学习内容，归纳概括探索并证明几何定理的基本思路，抓住新知课的核心知识，及解决的关键问题，从中提炼解题的基本策略，体验数学思想方法.

3 几何定理教学的思考

核心素养侧重学生自身在实践中的摸索、积累和体悟，是一个动态优化的过程，最终目标是培养学生可伴随终身可持续发展的能力和品格.数学核心素养的培养贯穿整个数学课程，几何定理教学应充分发挥其育人价值和功能.

3.1 分—割—剪—拼，培养空间观念和几何直观

本节课从问题导入→新知探究→变式应用，首尾贯穿“分→割→剪→拼”的动手操作实验验证的探索思路，融合图形旋转变换，运用动态的观点引导学生探究几何定理，帮助学生构建空间观念，培养几何直观并渗透模型思想，重视引领学生对几何定理获得的过程体验，积累活动经验，为今后灵活运用几何知识解决数学问题奠定基础，也是培养形象思维和动态观念的重要理念和途径.

3.2 观察—分析—猜想—论证，培养合情推理和演绎推理能力

本节课在新知探究环节设计了五个教学步骤，让学生亲历“构造新图形→观察新图形→分析新图形→提出猜想→证明猜想”这一过程，运用合情推理分析提出三角形中位线定理，运用演绎推理证明三角形中位线定理，两者相辅相成，促进定理的发现与论证.

教师创造性地使用教材，在问题导入环节启迪学生在研究几何图形时，可以通过割补剪拼实现图形的相互转化；在新知探究环节，设计了将三角形沿中位线进行剪拼成平行四边形，在变式应用的拓展环节，设计了将一般四边形剪拼成平行四边形等一系列的动手实践活动，运用图形变换原理探索发现新知，并迁移变化深化运用.在几何定理教学中，培养学生自主发现问题提出问题的意识，培养独立思考、主动思考的习惯，培养归纳概括抽象的思维能力，发挥数学在培养人的应用意识和创新意识，发展思维水平的重要作用.因此，核心素养指向的几何定理教学是实现数学育人价值的重要教学内容.