一道中考几何压轴题的解法分析与推广

傅兰英

(杭州市西湖区教育发展研究院,浙江 杭州 310000)

1 原题呈现

例1在正方形ABCD中，点M是边AB的中点，点E在线段AM上(不与点A重合)，点F在边BC上，且AE=2BF，联结EF，以EF为边在正方形ABCD内作正方形EFGH．

1)若AB=4，当点E与点M重合时，求正方形EFGH的面积.

2)如图1，已知直线HG分别与边AD，BC交于点I，J，射线EH与射线AD交于点K．

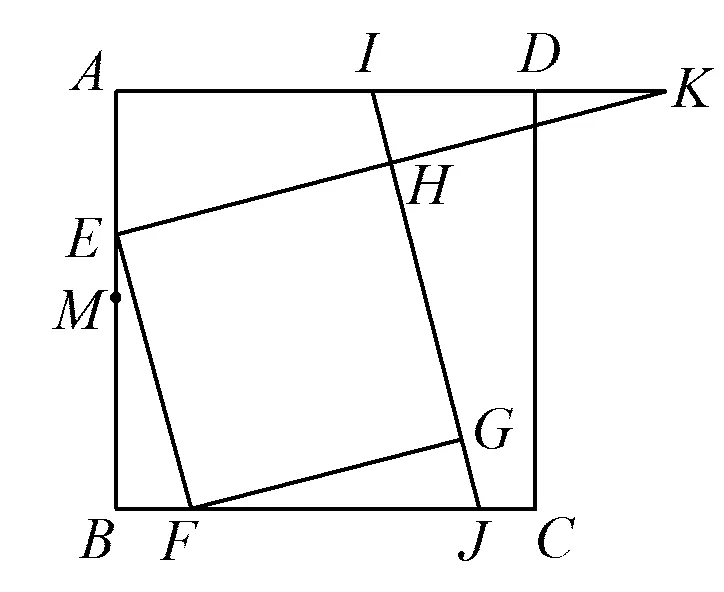
图1

①求证：EK=2EH；

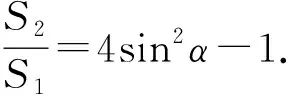
(2022年浙江省杭州市数学中考试题第23题)

2 证法展示

本文重点研究第2)小题第②题的证法.从命题视角看，本题融代数、几何、三角于一题的多种解法的命题导向，涵盖三角形全等、三角形相似、勾股定理、图形面积比与相似比的关系、三角函数应用等知识；考查了学生的构图能力、运算求解能力、推理论证能力，探索数量关系的不变性，从中归纳出代数表达；也考查了化归与转化思想、数形结合思想、特殊到一般思想.

从图形结构看，本题有“K”形全等与相似，还隐含弦图的结构，因此可以从多角度建立S1,S2之间的联系.

从解题思路上看，要求S1,S2的比值，常见的思路是整体构造和分别计算两种.鉴于以上分析，可以很自然地得到以下证法.

视角1整体构造，将面积比转化为线段比.

观察到△KHI≌△FGJ，且△KHI∽△KAE，利用相似三角形面积比等于相似比的平方切入破题．

证法1如图1，由第①小题得HK=GF.又因为

∠KHI=∠FGJ=90°， ∠KIH=∠FJG，

所以

△KHI≌△FGJ,

从而△KHI的面积为S1.由题意知

△KHI∽△KAE，

可得

故

视角2以算代证，分别计算出S1,S2.

证法2如图1，设正方形EFGH的边长为a．由题意知∠FJG=∠KEA=α，从而

可得

由HK=EH=a，∠KIH=∠AEK=α，可得

又EK=2EH=2a，可得

AE=2acosα，AK=2asinα，

从而

于是

因此

证法3(利用点H是EK的中点)如图2，过点H作HP⊥AD于点P．由∠A=90°，且KH=HE，可得

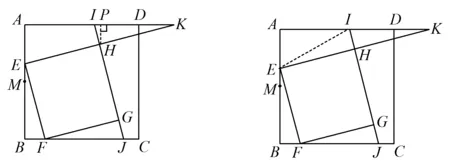
图2 图3

S△AEK=4S△PHK=2HK·HI·sin2α,

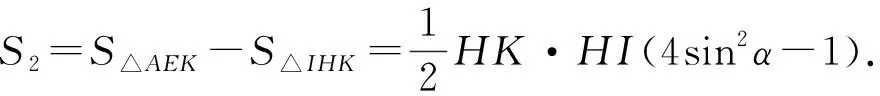
由解法1知△KHI≌△FGJ,从而

于是

S2=S1(4sin2α-1)，

因此

证法4如图3，设正方形EFGH的边长为a．联结IE，则

△IHK≌△IHE，

从而

EH=HK,IE=IK．

由题意知

∠FJG=∠KEA=α，

从而

于是

又

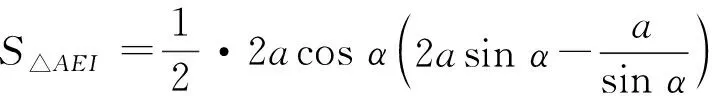
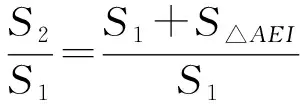
=4sin2α-1．

证法5如图4，设正方形EFGH的边长为a．由题意知

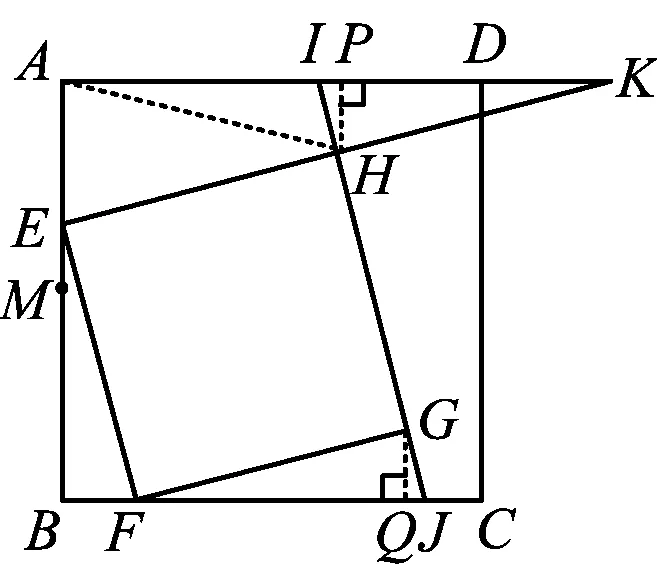
图4

∠FJG=∠KEA=α，

从而

于是

联结AH，由第①小题知

AH=EH=a，

可得

∠AEK=∠HAE=α，

从而

∠AHE=180°-2α， ∠AHI=2α-90°，

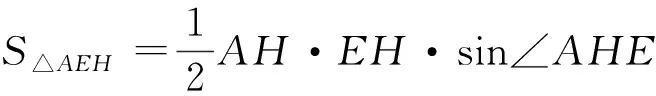
过点G作GQ⊥BC于点Q，过点H作HP⊥AD于点P.易证

△PHI≌△QGJ，

即

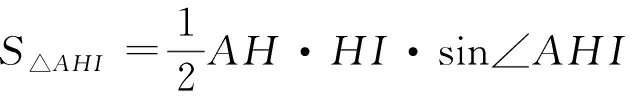
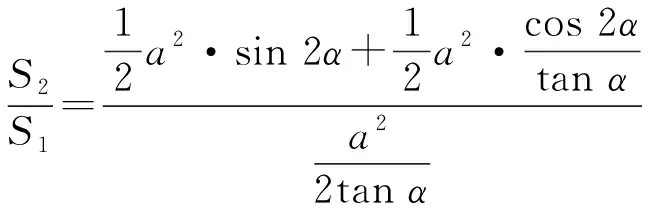
=2sinα·cosα·tanα+2sin2α-1

=4sin2α-1．

证法6(利用“K”形相似建立S1,S2的联系)如图5，过点H作HL⊥AE于点L，作HP⊥AK于点P，过点G作GQ⊥BC于点Q.

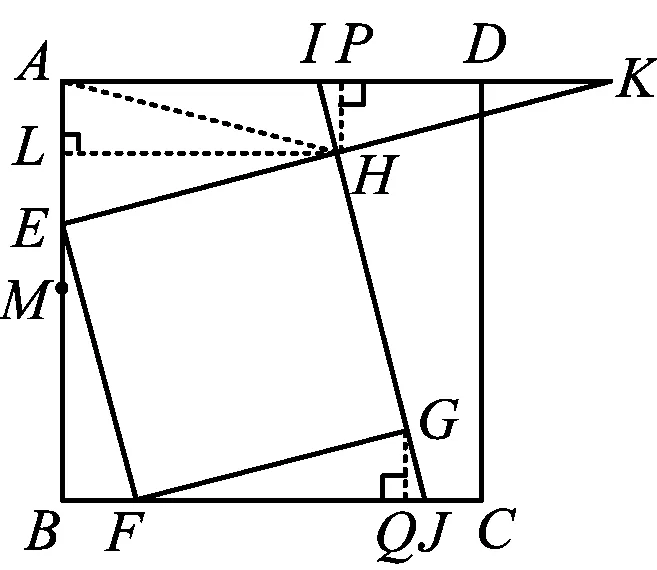
图5

设BF=a，BE=b，EF=c，△BEF的面积为S，△GQJ的面积为S′．由题意知△GQJ∽△EBF，△BEF∽△GFJ，从而

又H是KE的中点，可知

由勾股定理，得

a2=c2-b2，

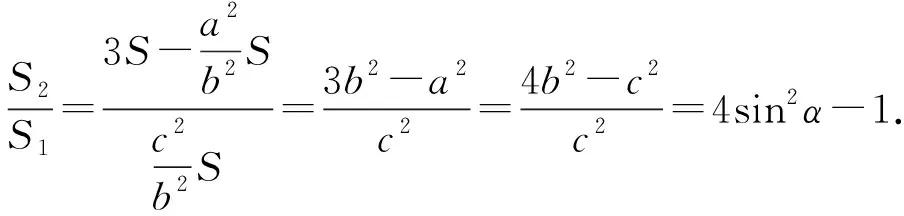
证法7(根据出入相补原理，结合图形内含的弦图结构破题)如图5，过点H分别作HL⊥AB于点L，作HP⊥AD于点P，过点G作GQ⊥BC于点Q，联结AH．由第①小题得

△HEL≌△EFB，

同理可得

△FGQ≌△EFB．

设△BEF的面积为S，则

S△HEL=S△FGQ=S,

由点H为KE的中点，可知

S1+S2=4S．

易证△PIH≌△QJG，△BEF∽△GFJ，从而

即

于是

故

评注本题通过添加辅助线将所求问题与已学知识联系起来，培养学生多种途径分析问题和解决问题的能力，体验了解决问题方法的多样性.在复杂图形中识别基本图形，能更快获得解题思路.

3 试题推广

试题条件改变，还可发现结论具有规律性：

……

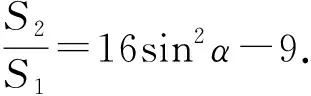
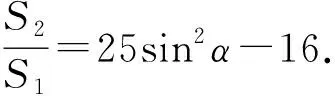
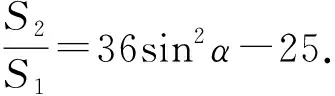
变式n若AE=nBF(其中n是正整数)，则

识破庐山真面目，从倍数2到n，算是对数学问题进行形式化，而形式化也是数学的基本特征之一.在数学教学中，学习形式化的表达是一项基本要求，但是不能只限于形式化的表达，要强调对数学本质的认识，否则会将生动活泼的数学思维活动淹没在形式化的海洋里.

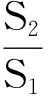
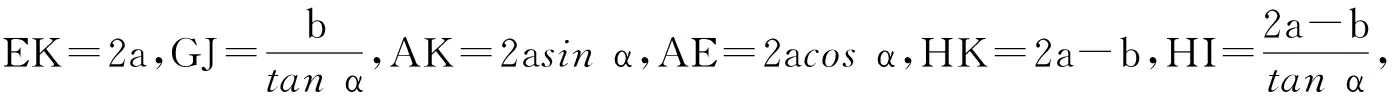
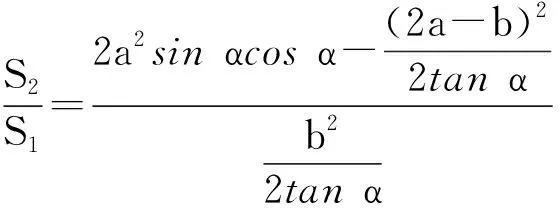
=4k2sin2α-(2k-1)2.

4 类比研究

如图6，在△ABC中，AD为边BC上的中线，线段BE交中线AD于点F，交线段AC于点E，若AE∶AC=1:2，求AF∶AD的值.

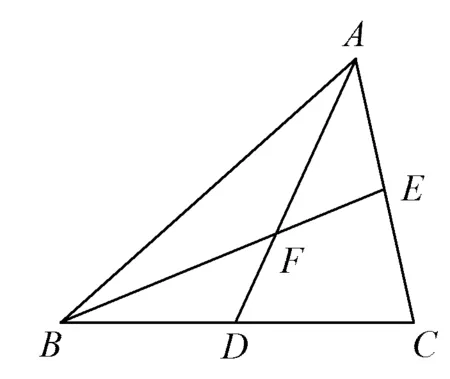
图6

分析图中有6个点：A，B，C，D，E，F；共有5条线段：AB，AC，BC，AD，BE.

追问辅助线怎么添？

教师引导学生有序思考问题，学生添加辅助线的方案如下:

1)过点E作辅助线(如图7)；

图7

2)过点D作辅助线(如图8)；

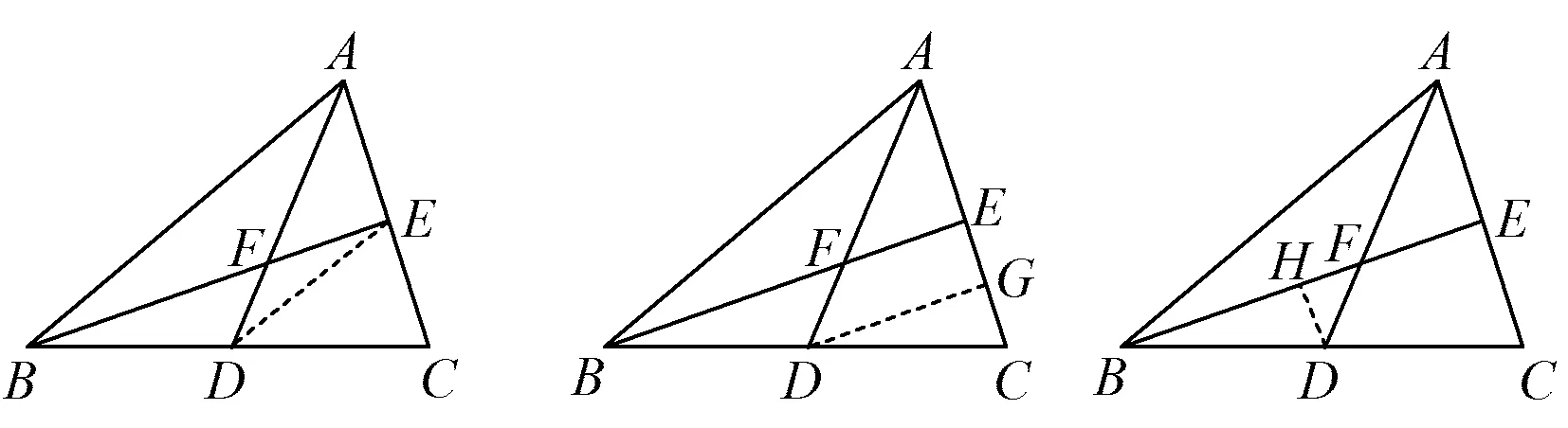
图8

3)过点A作辅助线(如图9)；

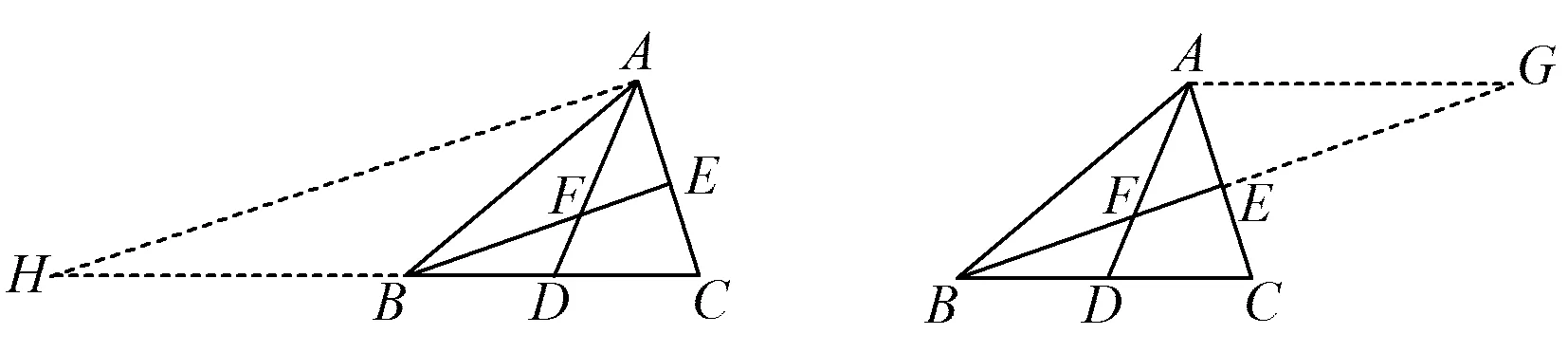
图9

4)过点B作辅助线(如图10)；

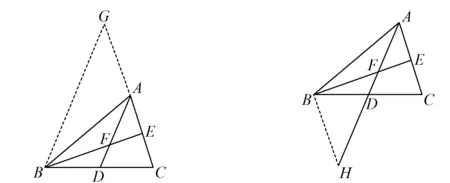
图10

5)过点C作辅助线(如图11).

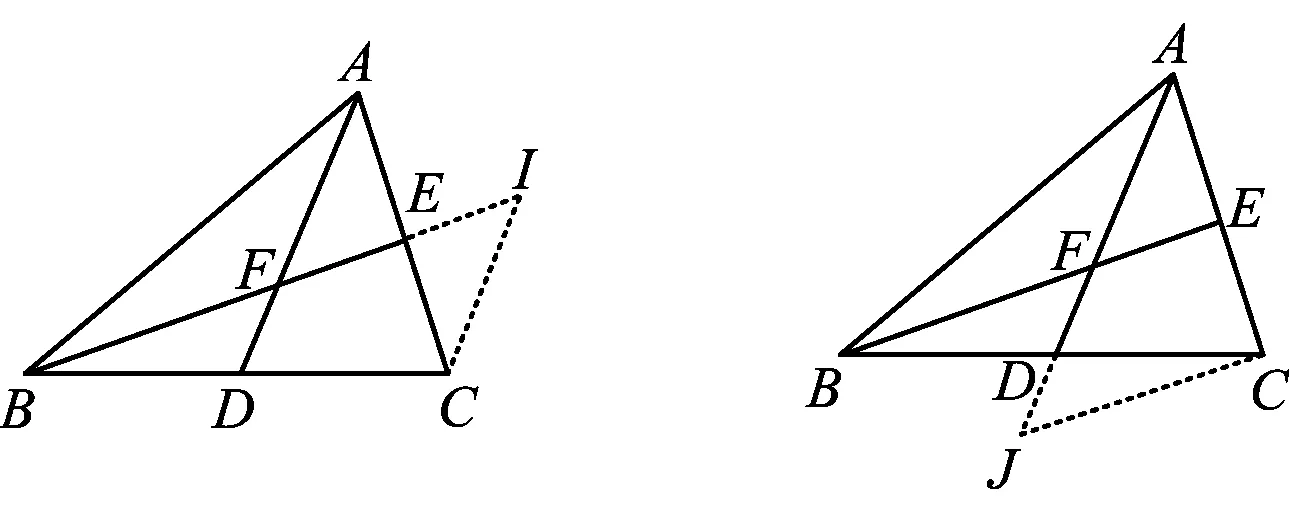
图11

思考辅助线如何添比较简捷？

此题能否拓展到一般？即改AE∶AC=1∶n，求AF∶FD的值.

……

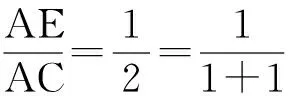
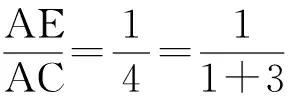
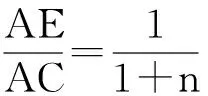
本题让学生完整经历猜测、操作、结论、完善、验证的过程，通过体验性活动进行知识建构，研究各种各样不同的可能解决问题的方法，归纳总结最佳方案，提升学生的直观想象能力.在运用各种添辅助线解决问题时，教师可以了解学生在问题解决过程中的知识储备和思维方式，引导学生从低阶思维向高阶思维迁移，由发散性思维到聚合性思维转变．

通过对本题的探究与推广，笔者想起数学家波利亚所说：“类比是一个领路人.”帮助寻找数学发现与数学求解的线索，激励我们多角度地探究与其他问题的联系，比如多元与少元、高维与低维、有限与无限等背景下的问题的本质有何不同等．

5 结束语

中考几何压轴题内涵丰富，我们不应仅停留在解题层面，而要用心挖掘问题本质和更有价值的问题，构建图形之间丰富的几何结构与代数表达之间的关联，这是寻找平面几何解题思路的一把“钥匙”．

大数学家希尔伯特曾说：“正是通过这些问题的解决，研究者锻炼其意志，发现新方法和新观点达到更为广阔自由的境界.”当我们完成一个数学问题的解答后，想一想这个问题与其他问题是否有联系？如何从整体入手，获得通性通法？如何从分析局部，优化方法？如何结构联想，获得灵感，进行推广与类比研究？通过研究、反思达到问题创新、思维创新和方法创新．

教学中要重视培养学生数学思想方法的发生、生成、内化、升华的过程，这是数学基本功的“内力”，教师要善于学习，高位审视问题，深刻识别隐藏在试题背后的数学思想，挖掘其中有价值的东西传授给学生，做到“会当凌绝顶，一览众山小”．